Chapter 7 Linear Programming Models Graphical and Computer

Chapter 7 Linear Programming Models: Graphical and Computer Methods To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -1 1

Learning Objectives Students will be able to: • Understand the basic assumptions and properties of linear programming (LP). • Formulate small to moderatesized LP problems. • Graphically solve any LP problem with two variables by both the corner point and isoline methods. To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -2 2

Learning Objectives continued • Understand special issues in LP - infeasibility, unboundedness, redundancy, and alternative optima. • Understand the role of sensitivity analysis. • Use Excel spreadsheets to solve LP problems. To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -3 3

Chapter Outline 7. 1 Introduction 7. 2 Requirements of a Linear Programming Problem 7. 3 Formulating LP Problems 7. 4 Graphical Solution to an LP Problem 7. 5 Solving Flair Furniture’s LP Problem using QM for Windows and Excel To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -4 4

Chapter Outline continued 7. 6 Solving Minimization Problems 7. 7 Four Special Cases 7. 8 Sensitivity Analysis in LP To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -5 5

Examples of Successful LP Applications 1. Development of a production schedule that will satisfy future demands for a firm’s production and at the same time minimize total production and inventory costs 2. Selection of the product mix in a factory to make best use of machinehours and labor-hours available while maximizing the firm’s products To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -6 6

Examples of Successful LP Applications 3. Determination of grades of petroleum products to yield the maximum profit 4. Selection of different blends of raw materials to feed mills to produce finished feed combinations at minimum cost 5. Determination of a distribution system that will minimize total shipping cost from several warehouses to various market locations To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -7 7

Requirements of a Linear Programming Problem • All problems seek to maximize or minimize some quantity (the objective function). • The presence of restrictions or constraints, limits the degree to which we can pursue our objective. • There must be alternative courses of action to choose from. • The objective and constraints in linear programming problems must be expressed in terms of linear equations or inequalities. To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -8 8

Basic Assumptions of Linear Programming • Certainty • Proportionality • Additivity • Divisibility • Nonnegativity To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -9 9

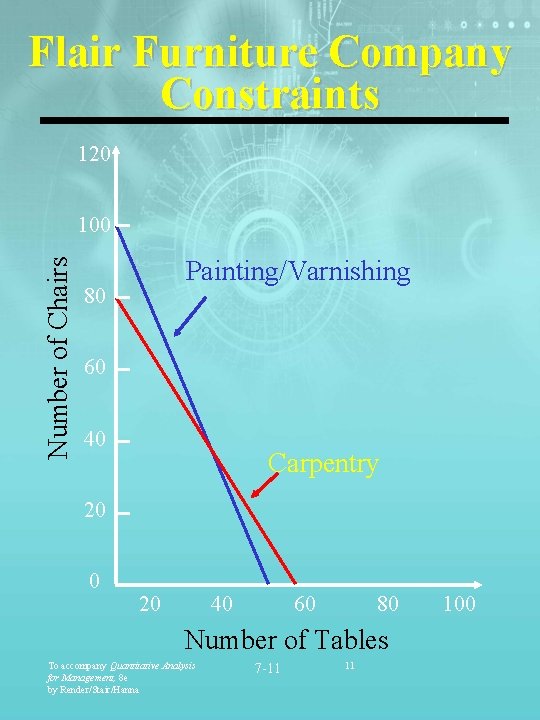
Flair Furniture Company Data - Table 7. 1 Hours Required to Produce One Unit T C Tables Chairs Department Carpentry Painting &Varnishing 4 2 3 1 Profit Amount $7 $5 Available Hours This Week 240 100 Constraints: 4 T + 3 C 240 (Carpentry) 2 T + 1 C 100 (Paint & Varnishing) Objective: Max: 7 T + 5 C To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -10 10

Flair Furniture Company Constraints 120 Number of Chairs 100 Painting/Varnishing 80 60 40 Carpentry 20 0 20 40 60 80 Number of Tables To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -11 11 100

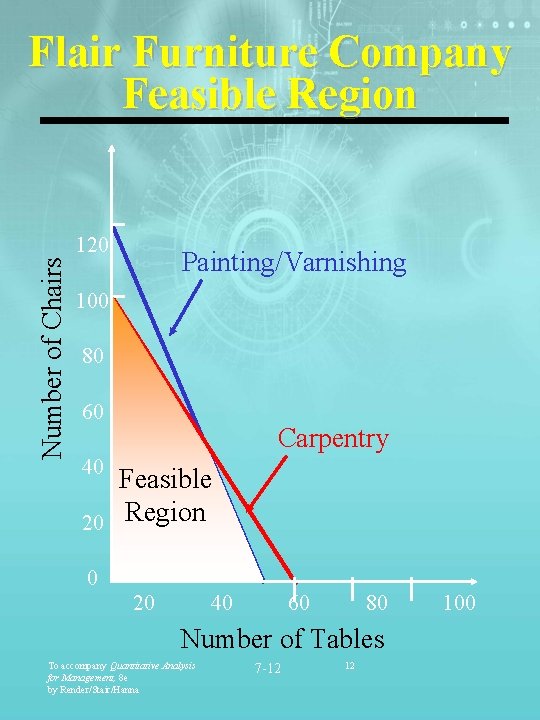
Number of Chairs Flair Furniture Company Feasible Region 120 Painting/Varnishing 100 80 60 40 20 Carpentry Feasible Region 0 20 40 60 80 Number of Tables To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -12 12 100

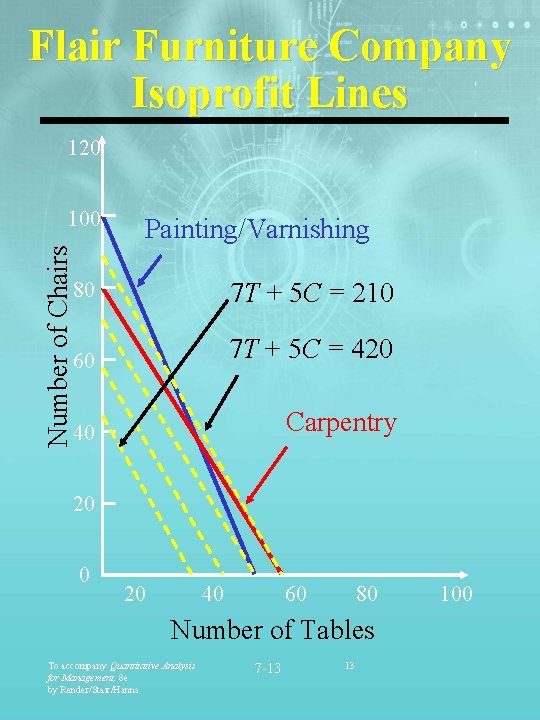
Flair Furniture Company Isoprofit Lines 120 Number of Chairs 100 Painting/Varnishing 80 7 T + 5 C = 210 60 7 T + 5 C = 420 40 Carpentry 20 0 20 40 60 80 Number of Tables To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -13 13 100

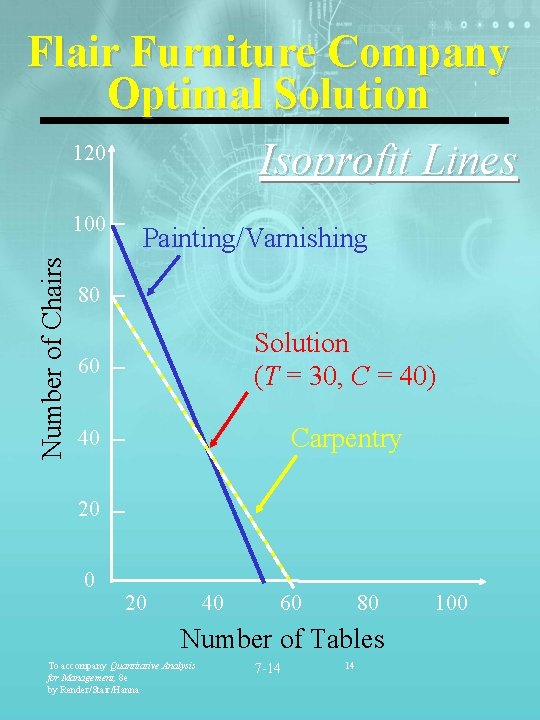
Flair Furniture Company Optimal Solution 120 Isoprofit Lines Number of Chairs 100 Painting/Varnishing 80 60 Solution (T = 30, C = 40) 40 Carpentry 20 0 20 40 60 80 Number of Tables To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -14 14 100

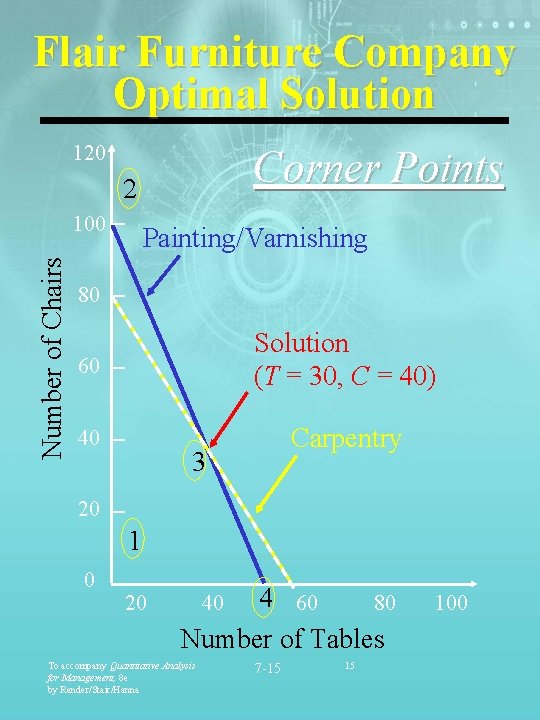
Flair Furniture Company Optimal Solution 120 Corner Points 2 Number of Chairs 100 Painting/Varnishing 80 60 Solution (T = 30, C = 40) 40 Carpentry 3 20 1 0 20 4 60 80 Number of Tables To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 40 7 -15 15 100

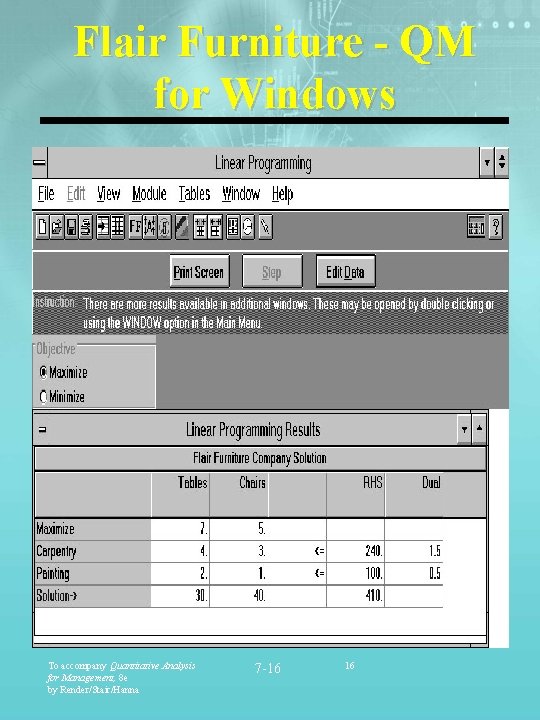
Flair Furniture - QM for Windows To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -16 16

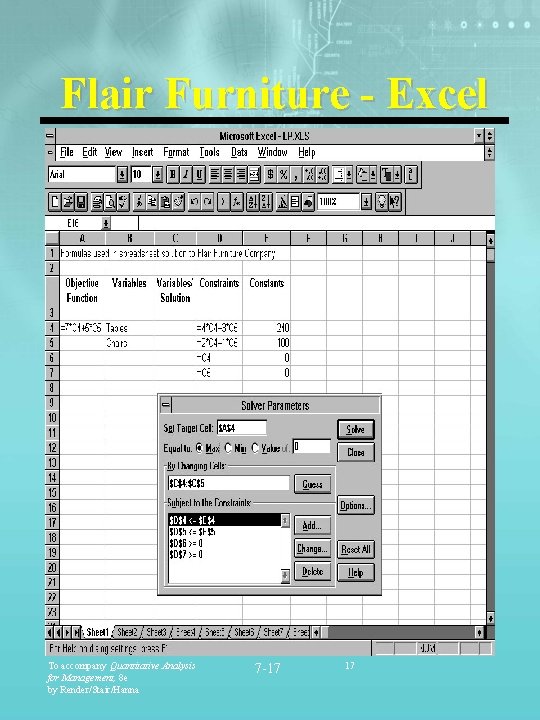
Flair Furniture - Excel To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -17 17

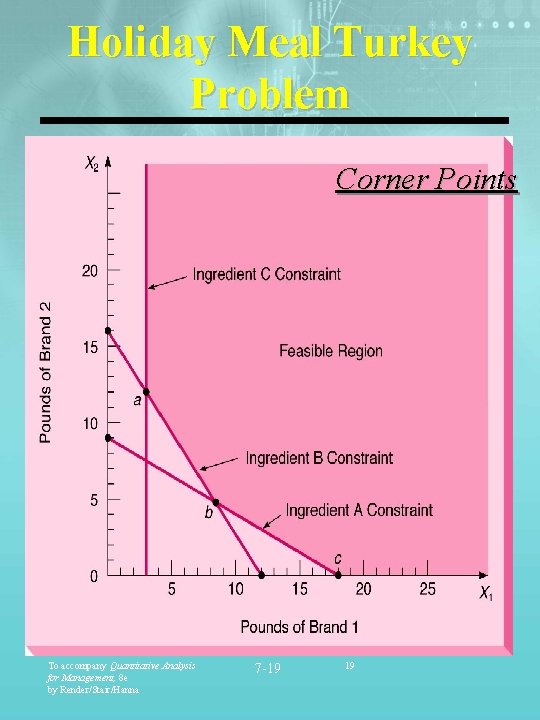
Holiday Meal Turkey Ranch Minimize: 2 X 1 + 3 X 2 Subject to : 5 X 1 + 10 X 2 ³ 90 ( A) 4 X 1 + 3 X 2 ³ 48 (B) ³ 1 1/2 (C) ½ X 1 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -18 18

Holiday Meal Turkey Problem Corner Points To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -19 19

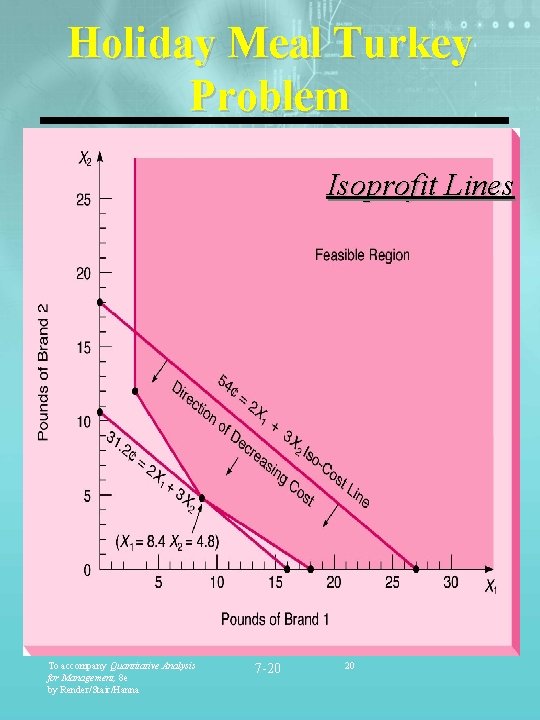
Holiday Meal Turkey Problem Isoprofit Lines To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -20 20

Special Cases in LP • Infeasibility • Unbounded Solutions • Redundancy • Degeneracy • More Than One Optimal Solution To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -21 21

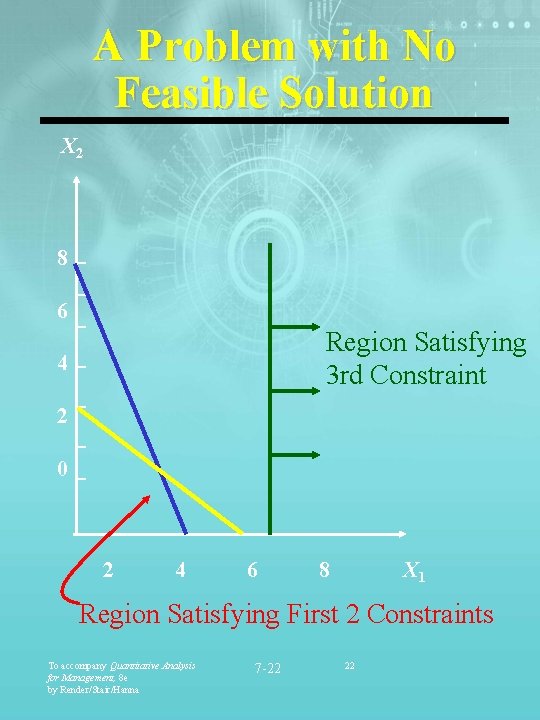
A Problem with No Feasible Solution X 2 8 6 Region Satisfying 3 rd Constraint 4 2 0 2 4 6 8 X 1 Region Satisfying First 2 Constraints To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -22 22

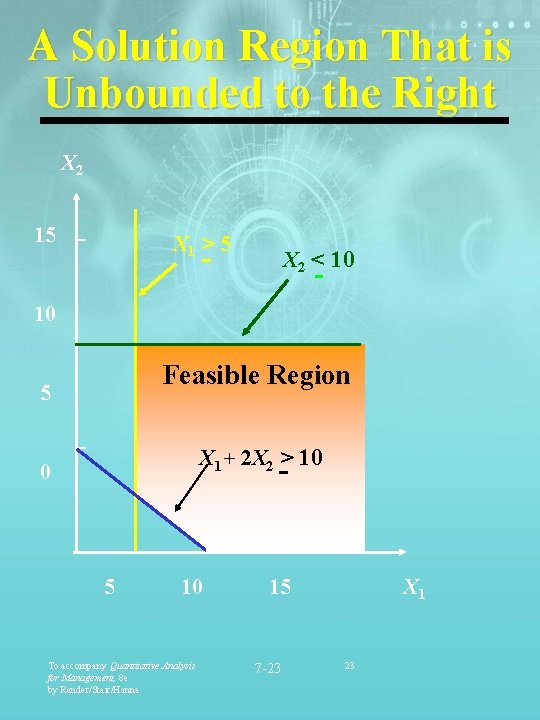
A Solution Region That is Unbounded to the Right X 2 15 X 1 > 5 X 2 < 10 10 Feasible Region 5 X 1 + 2 X 2 > 10 0 5 10 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 15 7 -23 X 1 23

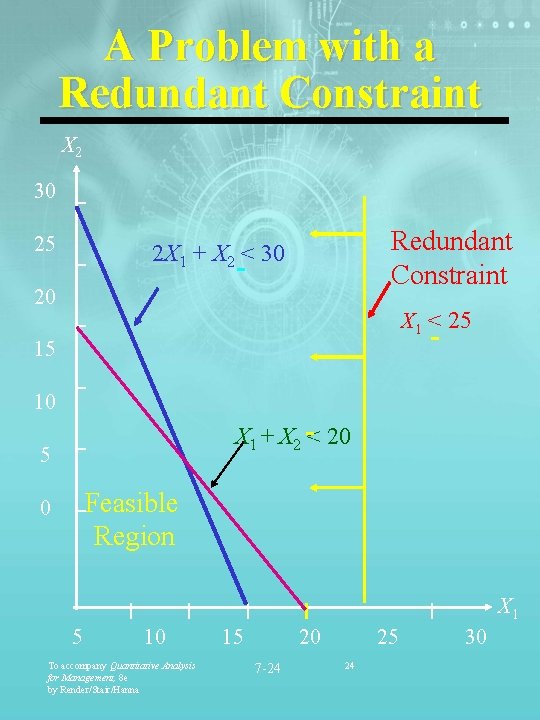
A Problem with a Redundant Constraint X 2 30 25 Redundant Constraint 2 X 1 + X 2 < 30 20 X 1 < 25 15 10 X 1 + X 2 < 20 5 Feasible Region 0 X 1 5 10 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 15 20 7 -24 25 24 30

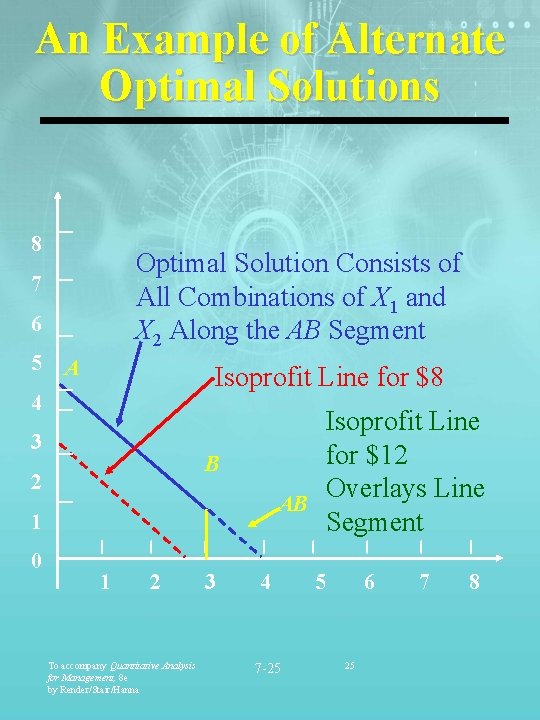
An Example of Alternate Optimal Solutions 8 Optimal Solution Consists of All Combinations of X 1 and X 2 Along the AB Segment 7 6 5 A Isoprofit Line for $8 4 3 B 2 AB 1 0 Isoprofit Line for $12 Overlays Line Segment 1 2 To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 3 4 7 -25 5 6 25 7 8

Sensitivity Analysis • Changes in the Objective Function Coefficient • Changes in Resources (RHS) • Changes in Technological Coefficients To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 7 -26 26

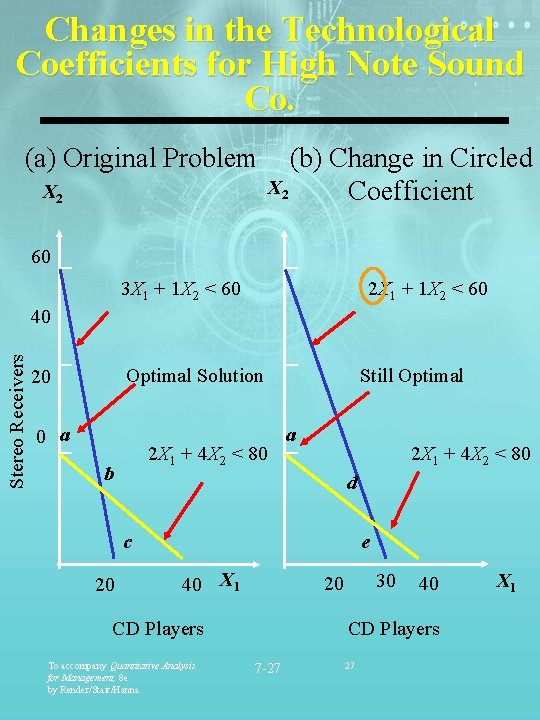
Changes in the Technological Coefficients for High Note Sound Co. (a) Original Problem X 2 (b) Change in Circled X 2 Coefficient 60 2 X 1 + 1 X 2 < 60 3 X 1 + 1 X 2 < 60 Stereo Receivers 40 Optimal Solution 20 0 a 2 X 1 + 4 X 2 < 80 b Still Optimal a 2 X 1 + 4 X 2 < 80 d c 20 e 40 X 1 CD Players To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 30 20 40 CD Players 7 -27 27 X 1

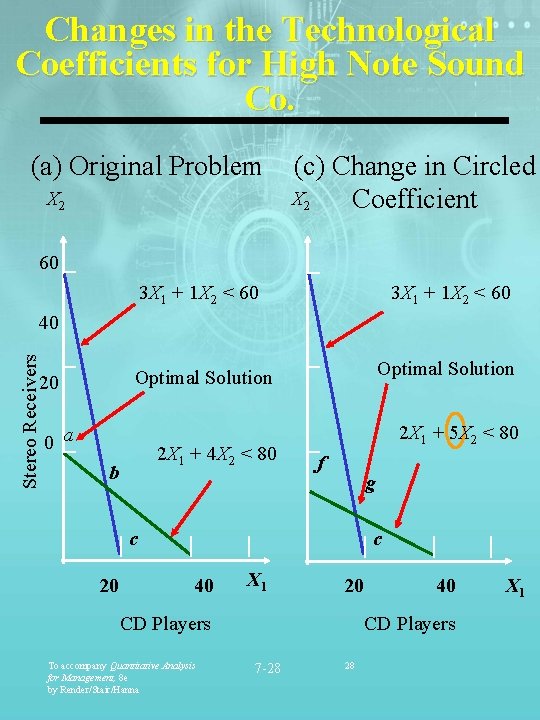
Changes in the Technological Coefficients for High Note Sound Co. (a) Original Problem X 2 (c) Change in Circled X 2 Coefficient 60 3 X 1 + 1 X 2 < 60 Optimal Solution Stereo Receivers 40 20 0 a 2 X 1 + 4 X 2 < 80 b 2 X 1 + 5 X 2 < 80 f g c 20 c 40 X 1 20 CD Players To accompany Quantitative Analysis for Management, 8 e by Render/Stair/Hanna 40 CD Players 7 -28 28 X 1