Chapter 7 Linear Programming Models Graphical and Computer

Chapter 7 Linear Programming Models: Graphical and Computer Methods To accompany Quantitative Analysis for Management, Tenth Edition, by Render, Stair, and Hanna Power Point slides created by Jeff Heyl © 2008 Prentice-Hall, Inc. © 2009 Prentice-Hall, Inc.

Introduction n Many management decisions involve trying to make the most effective use of limited resources n Machinery, labor, money, time, warehouse space, raw materials n Linear programming (LP) LP is a widely used mathematical modeling technique designed to help managers in planning and decision making relative to resource allocation n Belongs to the broader field of mathematical programming n In this sense, programming refers to modeling and solving a problem mathematically © 2009 Prentice-Hall, Inc. 7– 2

Requirements of a Linear Programming Problem n LP has been applied in many areas over the past 50 years n All LP problems have 4 properties in common 1. All problems seek to maximize or minimize some quantity (the objective function) function 2. The presence of restrictions or constraints that limit the degree to which we can pursue our objective 3. There must be alternative courses of action to choose from 4. The objective and constraints in problems must be expressed in terms of linear equations or inequalities © 2009 Prentice-Hall, Inc. 7– 3

Examples of Successful LP Applications n Development of a production schedule that will n satisfy future demands for a firm’s production n while minimizing total production and inventory costs n Determination of grades of petroleum products to yield the maximum profit n Selection of different blends of raw materials to feed mills to produce finished feed combinations at minimum cost n Determination of a distribution system that will minimize total shipping cost from several warehouses to various market locations © 2009 Prentice-Hall, Inc. 7– 4

LP Properties and Assumptions PROPERTIES OF LINEAR PROGRAMS 1. One objective function 2. One or more constraints 3. Alternative courses of action 4. Objective function and constraints are linear ASSUMPTIONS OF LP 1. Certainty 2. Proportionality 3. Additivity 4. Divisibility 5. Nonnegative variables Table 7. 1 © 2009 Prentice-Hall, Inc. 7– 5

Basic Assumptions of LP n We assume conditions of certainty exist and numbers in the objective and constraints are known with certainty and do not change during the period being studied n We assume proportionality exists in the objective and constraints § constancy between production increases and resource utilization – if 1 unit needs 3 hours then 10 require 30 hours n We assume additivity in that the total of all activities equals the sum of the individual activities n We assume divisibility in that solutions need not be whole numbers n All answers or variables are nonnegative as we are dealing with real physical quantities © 2009 Prentice-Hall, Inc. 7– 6

Formulating LP Problems n Formulating a linear program involves developing a mathematical model to represent the managerial problem n The steps in formulating a linear program are 1. Completely understand the managerial problem being faced 2. Identify the objective and constraints 3. Define the decision variables 4. Use the decision variables to write mathematical expressions for the objective function and the constraints © 2009 Prentice-Hall, Inc. 7– 7

Formulating LP Problems n One of the most common LP applications is the product mix problem n Two or more products are produced using limited resources such as personnel, machines, and raw materials n The profit that the firm seeks to maximize is based on the profit contribution per unit of each product n The company would like to determine how many units of each product it should produce so as to maximize overall profit given its limited resources © 2009 Prentice-Hall, Inc. 7– 8

Flair Furniture Company n The Flair Furniture Company produces n n n inexpensive tables and chairs Processes are similar in that both require a certain amount of hours of carpentry work and in the painting and varnishing department Each table takes 4 hours of carpentry and 2 hours of painting and varnishing Each chair requires 3 of carpentry and 1 hour of painting and varnishing There are 240 hours of carpentry time available and 100 hours of painting and varnishing Each table yields a profit of $70 and each chair a profit of $50 © 2009 Prentice-Hall, Inc. 7– 9

Flair Furniture Company n The company wants to determine the best combination of tables and chairs to produce to reach the maximum profit HOURS REQUIRED TO PRODUCE 1 UNIT DEPARTMENT (T) TABLES (C) CHAIRS AVAILABLE HOURS THIS WEEK Carpentry 4 3 240 Painting and varnishing 2 1 100 $70 $50 Profit per unit Table 7. 2 © 2009 Prentice-Hall, Inc. 7 – 10

Flair Furniture Company n The objective is to Maximize profit n The constraints are 1. The hours of carpentry time used cannot exceed 240 hours per week 2. The hours of painting and varnishing time used cannot exceed 100 hours per week n The decision variables representing the actual decisions we will make are T = number of tables to be produced per week C = number of chairs to be produced per week © 2009 Prentice-Hall, Inc. 7 – 11

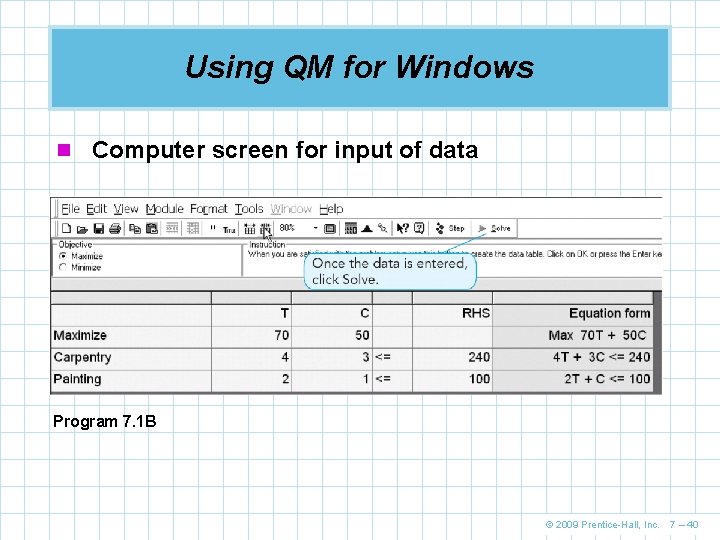
Flair Furniture Company n We create the LP objective function in terms of T and C Maximize profit = $70 T + $50 C n Develop mathematical relationships for the two constraints n For carpentry, total time used is (4 hours per table)(Number of tables produced) + (3 hours per chair)(Number of chairs produced) n We know that Carpentry time used ≤ Carpentry time available 4 T + 3 C ≤ 240 (hours of carpentry time) © 2009 Prentice-Hall, Inc. 7 – 12

Flair Furniture Company n Similarly Painting and varnishing time used ≤ Painting and varnishing time available 2 T + 1 C ≤ 100 (hours of painting and varnishing time) This means that each table produced requires two hours of painting and varnishing time n Both of these constraints restrict production capacity and affect total profit © 2009 Prentice-Hall, Inc. 7 – 13

Flair Furniture Company n The values for T and C must be nonnegative T ≥ 0 (number of tables produced is greater than or equal to 0) C ≥ 0 (number of chairs produced is greater than or equal to 0) n The complete problem stated mathematically Maximize profit = $70 T + $50 C subject to 4 T + 3 C ≤ 240 (carpentry constraint) 2 T + 1 C ≤ 100 (painting and varnishing constraint) T, C ≥ 0 (nonnegativity constraint) © 2009 Prentice-Hall, Inc. 7 – 14

Graphical Solution to an LP Problem n The easiest way to solve a small LP problems is with the graphical solution approach n The graphical method only works when there are just two decision variables n When there are more than two variables, a more complex approach is needed as it is not possible to plot the solution on a twodimensional graph n The graphical method provides valuable insight into how other approaches work © 2009 Prentice-Hall, Inc. 7 – 15

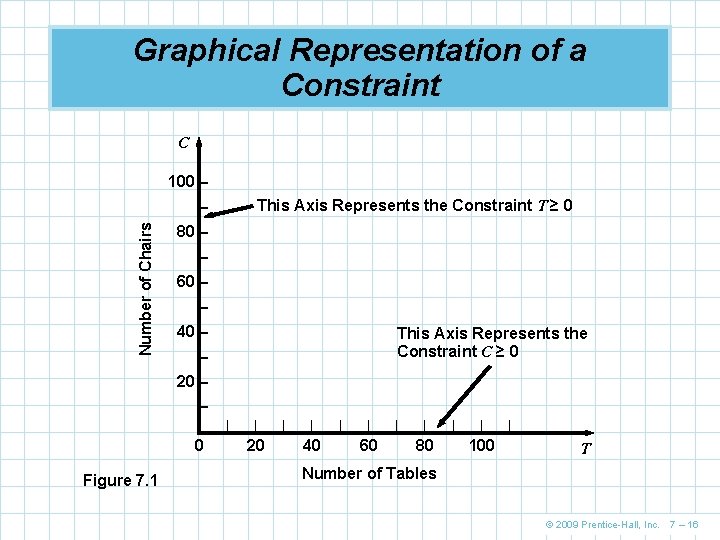
Graphical Representation of a Constraint C 100 – This Axis Represents the Constraint T ≥ 0 Number of Chairs – 80 – – 60 – – 40 – This Axis Represents the Constraint C ≥ 0 – 20 – – |– 0 Figure 7. 1 | | 20 | | 40 | | 60 | | 80 | | 100 | T Number of Tables © 2009 Prentice-Hall, Inc. 7 – 16

Graphical Representation of a Constraint n The first step in solving the problem is to identify a set or region of feasible solutions n To do this we plot each constraint equation on a graph n We start by graphing the equality portion of the constraint equations 4 T + 3 C = 240 n We solve for the axis intercepts and draw the line © 2009 Prentice-Hall, Inc. 7 – 17

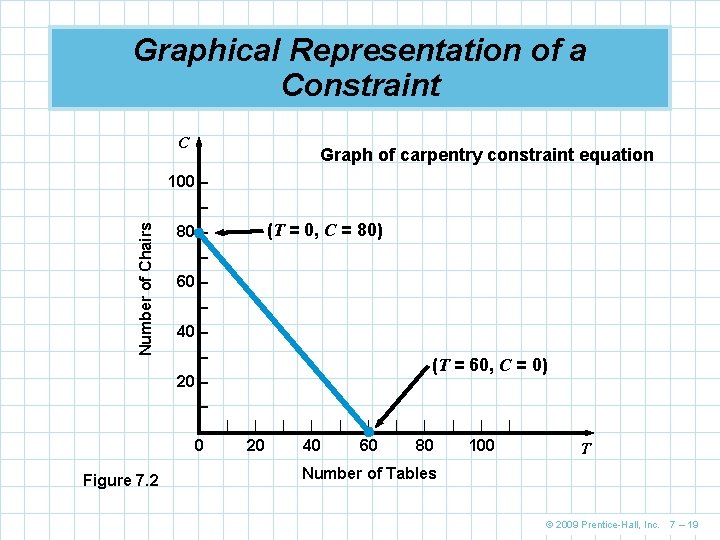
Graphical Representation of a Constraint n When Flair produces no tables, the carpentry constraint is 4(0) + 3 C = 240 C = 80 n Similarly for no chairs 4 T + 3(0) = 240 4 T = 240 T = 60 n This line is shown on the following graph © 2009 Prentice-Hall, Inc. 7 – 18

Graphical Representation of a Constraint C Graph of carpentry constraint equation 100 – Number of Chairs – (T = 0, C = 80) 80 – – 60 – – 40 – – (T = 60, C = 0) 20 – – |– 0 Figure 7. 2 | | 20 | | 40 | | 60 | | 80 | | 100 | T Number of Tables © 2009 Prentice-Hall, Inc. 7 – 19

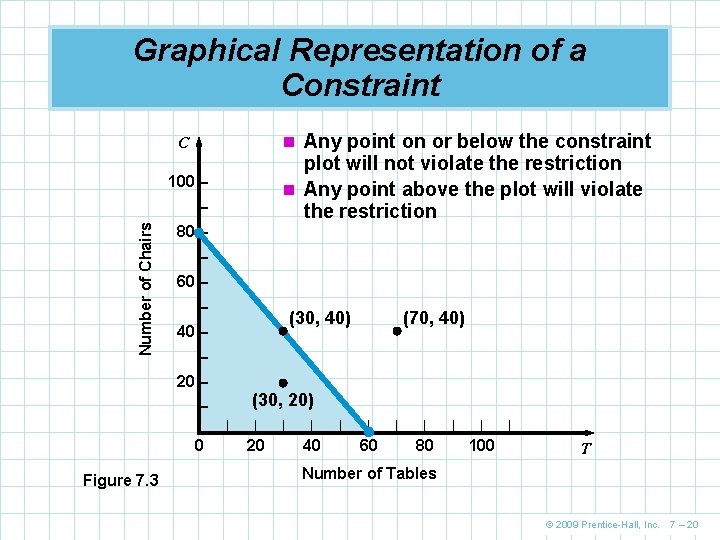
Graphical Representation of a Constraint n Any point on or below the constraint C plot will not violate the restriction n Any point above the plot will violate the restriction 100 – Number of Chairs – 80 – – 60 – – (30, 40) 40 – – 20 – (30, 20) – |– 0 Figure 7. 3 (70, 40) | | 20 | | 40 | | 60 | | 80 | | 100 | T Number of Tables © 2009 Prentice-Hall, Inc. 7 – 20

Graphical Representation of a Constraint n The point (30, 40) lies on the plot and exactly satisfies the constraint 4(30) + 3(40) = 240 n The point (30, 20) lies below the plot and satisfies the constraint 4(30) + 3(20) = 180 n The point (30, 40) lies above the plot and does not satisfy the constraint 4(70) + 3(40) = 400 © 2009 Prentice-Hall, Inc. 7 – 21

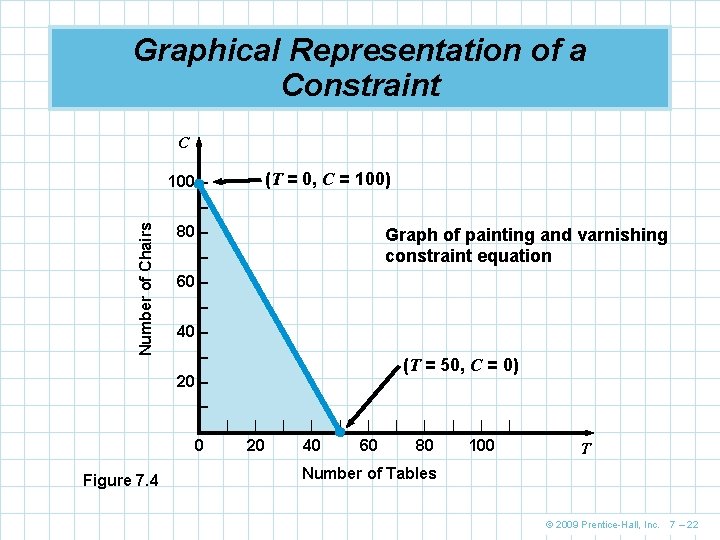
Graphical Representation of a Constraint C (T = 0, C = 100) 100 – Number of Chairs – 80 – Graph of painting and varnishing constraint equation – 60 – – 40 – – (T = 50, C = 0) 20 – – |– 0 Figure 7. 4 | | 20 | | 40 | | 60 | | 80 | | 100 | T Number of Tables © 2009 Prentice-Hall, Inc. 7 – 22

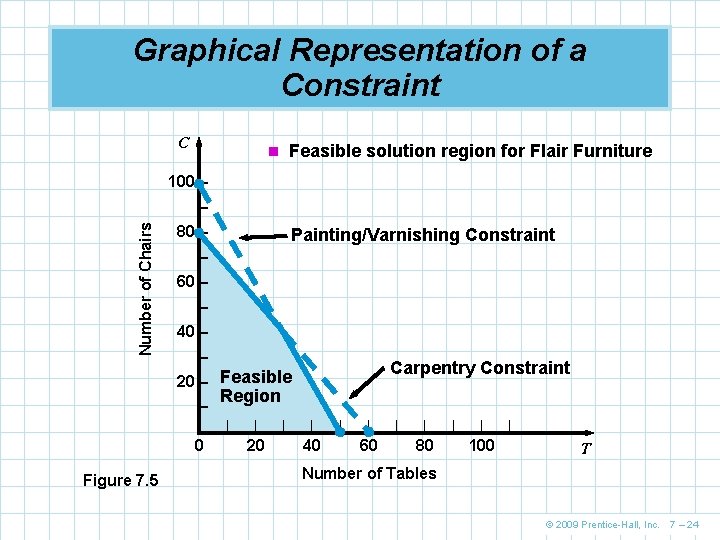
Graphical Representation of a Constraint n To produce tables and chairs, both n n n departments must be used We need to find a solution that satisfies both constraints simultaneously A new graph shows both constraint plots The feasible region (or area of feasible solutions) solutions is where all constraints are satisfied Any point inside this region is a feasible solution Any point outside the region is an infeasible solution © 2009 Prentice-Hall, Inc. 7 – 23

Graphical Representation of a Constraint C n Feasible solution region for Flair Furniture 100 – Number of Chairs – 80 – Painting/Varnishing Constraint – 60 – – 40 – – Carpentry Constraint 20 – Feasible – |– 0 Figure 7. 5 Region | | 20 | | 40 | | 60 | | 80 | | 100 | T Number of Tables © 2009 Prentice-Hall, Inc. 7 – 24

Graphical Representation of a Constraint n For the point (30, 20) Carpentry constraint 4 T + 3 C ≤ 240 hours available (4)(30) + (3)(20) = 180 hours used Painting constraint 2 T + 1 C ≤ 100 hours available (2)(30) + (1)(20) = 80 hours used n For the point (70, 40) Carpentry constraint 4 T + 3 C ≤ 240 hours available (4)(70) + (3)(40) = 400 hours used Painting constraint 2 T + 1 C ≤ 100 hours available (2)(70) + (1)(40) = 180 hours used © 2009 Prentice-Hall, Inc. 7 – 25

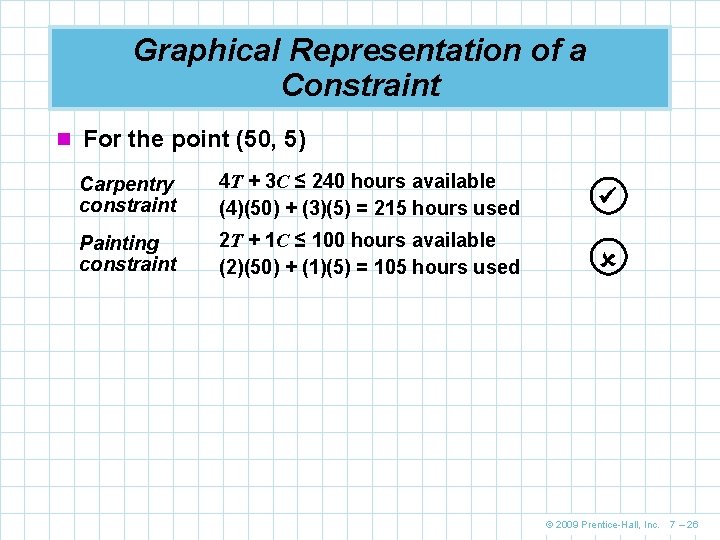
Graphical Representation of a Constraint n For the point (50, 5) Carpentry constraint 4 T + 3 C ≤ 240 hours available (4)(50) + (3)(5) = 215 hours used Painting constraint 2 T + 1 C ≤ 100 hours available (2)(50) + (1)(5) = 105 hours used © 2009 Prentice-Hall, Inc. 7 – 26

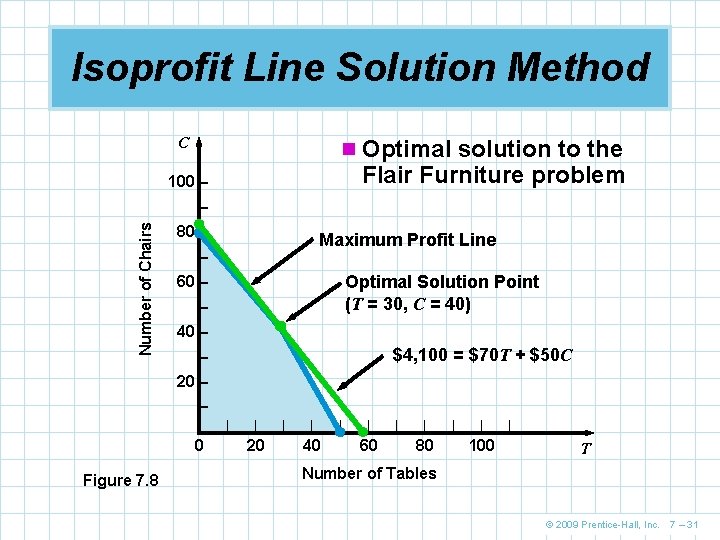
Isoprofit Line Solution Method n Once the feasible region has been graphed, we need n n to find the optimal solution from the many possible solutions The speediest way to do this is to use the isoprofit line method Starting with a small but possible profit value, we graph the objective function We move the objective function line in the direction of increasing profit while maintaining the slope The last point it touches in the feasible region is the optimal solution © 2009 Prentice-Hall, Inc. 7 – 27

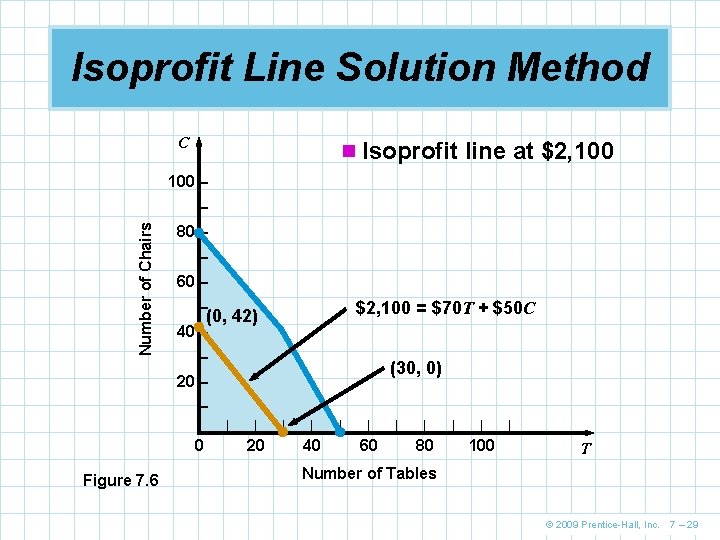
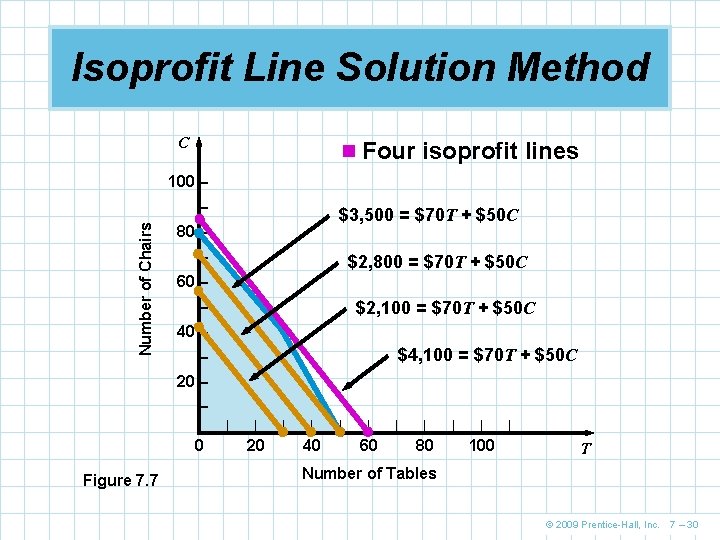
Isoprofit Line Solution Method n For Flair Furniture, choose a profit of $2, 100 n The objective function is then n n $2, 100 = 70 T + 50 C Solving for the axis intercepts, we can draw the graph This is obviously not the best possible solution Further graphs can be created using larger profits The further we move from the origin while maintaining the slope and staying within the boundaries of the feasible region, the larger the profit will be The highest profit ($4, 100) will be generated when the isoprofit line passes through the point (30, 40) © 2009 Prentice-Hall, Inc. 7 – 28

Isoprofit Line Solution Method C n Isoprofit line at $2, 100 – Number of Chairs – 80 – – 60 – – $2, 100 = $70 T + $50 C (0, 42) 40 – – (30, 0) 20 – – |– 0 Figure 7. 6 | | 20 | | 40 | | 60 | | 80 | | 100 | T Number of Tables © 2009 Prentice-Hall, Inc. 7 – 29

Isoprofit Line Solution Method C n Four isoprofit lines 100 – Number of Chairs – $3, 500 = $70 T + $50 C 80 – – $2, 800 = $70 T + $50 C 60 – – $2, 100 = $70 T + $50 C 40 – $4, 100 = $70 T + $50 C – 20 – – |– 0 Figure 7. 7 | | 20 | | 40 | | 60 | | 80 | | 100 | T Number of Tables © 2009 Prentice-Hall, Inc. 7 – 30

Isoprofit Line Solution Method C n Optimal solution to the Flair Furniture problem 100 – Number of Chairs – 80 – Maximum Profit Line – Optimal Solution Point (T = 30, C = 40) 60 – – 40 – $4, 100 = $70 T + $50 C – 20 – – |– 0 Figure 7. 8 | | 20 | | 40 | | 60 | | 80 | | 100 | T Number of Tables © 2009 Prentice-Hall, Inc. 7 – 31

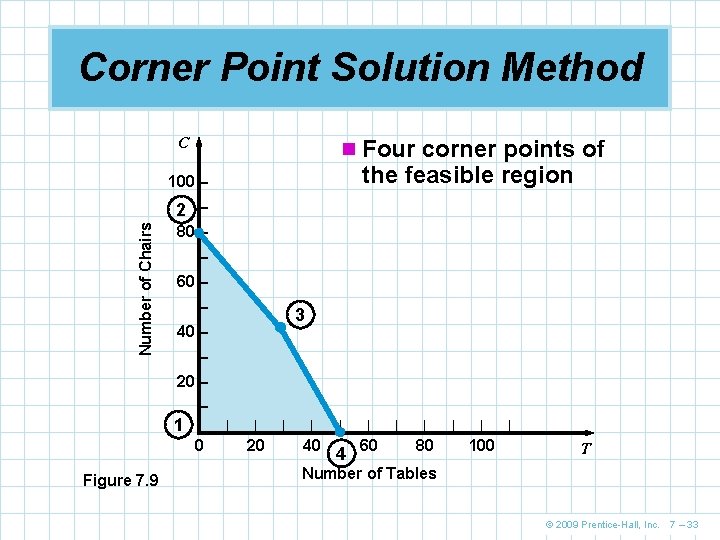
Corner Point Solution Method n A second approach to solving LP problems employs the corner point method n It involves looking at the profit at every corner point of the feasible region n The mathematical theory behind LP is that the optimal solution must lie at one of the corner points, points or extreme point, point in the feasible region n For Flair Furniture, the feasible region is a four-sided polygon with four corner points labeled 1, 2, 3, and 4 on the graph © 2009 Prentice-Hall, Inc. 7 – 32

Corner Point Solution Method C n Four corner points of the feasible region 100 – Number of Chairs 2 – 80 – – 60 – – 3 40 – – 20 – – 1 |– 0 Figure 7. 9 | | 20 | | 40 | 4 | 60 | | 80 | | 100 | T Number of Tables © 2009 Prentice-Hall, Inc. 7 – 33

Corner Point Solution Method Point 1 : (T = 0, C = 0) Profit = $70(0) + $50(0) = $0 Point 2 : (T = 0, C = 80) Profit = $70(0) + $50(80) = $4, 000 Point 4 : (T = 50, C = 0) Profit = $70(50) + $50(0) = $3, 500 Point 3 : (T = 30, C = 40) Profit = $70(30) + $50(40) = $4, 100 n Because Point 3 returns the highest profit, this is the optimal solution n To find the coordinates for Point 3 accurately we have to solve for the intersection of the two constraint lines n The details of this are on the following slide © 2009 Prentice-Hall, Inc. 7 – 34

Corner Point Solution Method n Using the simultaneous equations method, method we multiply the painting equation by – 2 and add it to the carpentry equation 4 T + 3 C = 240 – 4 T – 2 C = – 200 C = 40 (carpentry line) (painting line) n Substituting 40 for C in either of the original equations allows us to determine the value of T 4 T + (3)(40) = 240 4 T + 120 = 240 T = 30 (carpentry line) © 2009 Prentice-Hall, Inc. 7 – 35

Summary of Graphical Solution Methods ISOPROFIT METHOD 1. Graph all constraints and find the feasible region. 2. Select a specific profit (or cost) line and graph it to find the slope. 3. Move the objective function line in the direction of increasing profit (or decreasing cost) while maintaining the slope. The last point it touches in the feasible region is the optimal solution. 4. Find the values of the decision variables at this last point and compute the profit (or cost). CORNER POINT METHOD 1. Graph all constraints and find the feasible region. 2. Find the corner points of the feasible reason. 3. Compute the profit (or cost) at each of the feasible corner points. 4. select the corner point with the best value of the objective function found in Step 3. This is the optimal solution. Table 7. 3 © 2009 Prentice-Hall, Inc. 7 – 36

Solving Flair Furniture’s LP Problem Using QM for Windows and Excel n Most organizations have access to software to solve big LP problems n While there are differences between software implementations, the approach each takes towards handling LP is basically the same n Once you are experienced in dealing with computerized LP algorithms, you can easily adjust to minor changes © 2009 Prentice-Hall, Inc. 7 – 37

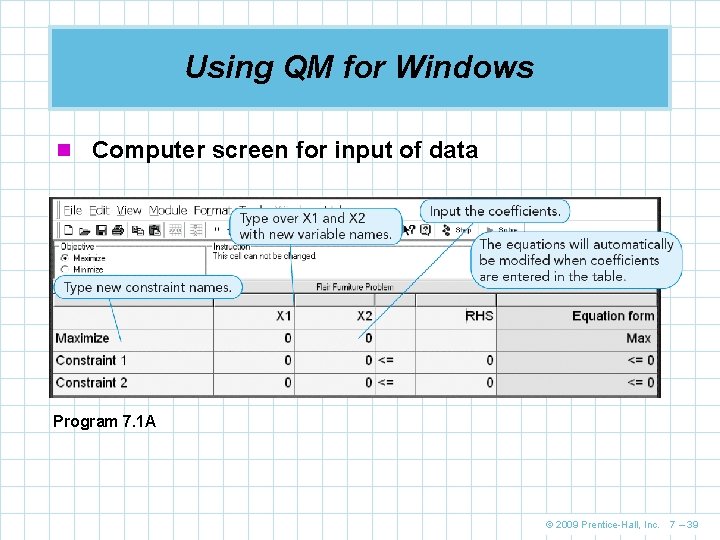
Using QM for Windows n First select the Linear Programming module n Specify the number of constraints (non-negativity is assumed) n Specify the number of decision variables n Specify whether the objective is to be maximized or minimized n For the Flair Furniture problem there are two constraints, two decision variables, and the objective is to maximize profit © 2009 Prentice-Hall, Inc. 7 – 38

Using QM for Windows n Computer screen for input of data Program 7. 1 A © 2009 Prentice-Hall, Inc. 7 – 39

Using QM for Windows n Computer screen for input of data Program 7. 1 B © 2009 Prentice-Hall, Inc. 7 – 40

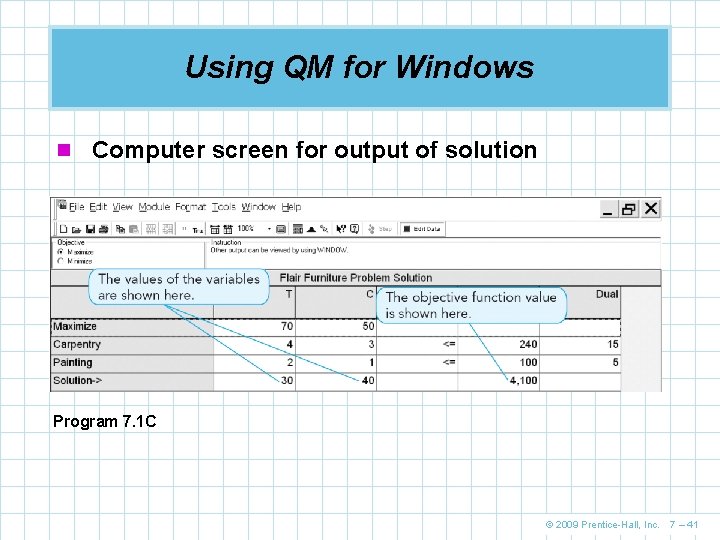
Using QM for Windows n Computer screen for output of solution Program 7. 1 C © 2009 Prentice-Hall, Inc. 7 – 41

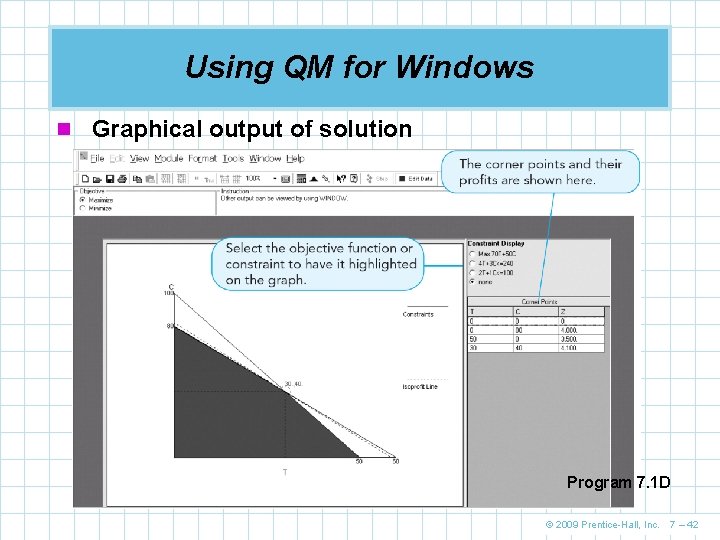
Using QM for Windows n Graphical output of solution Program 7. 1 D © 2009 Prentice-Hall, Inc. 7 – 42

Solving Minimization Problems n Many LP problems involve minimizing an objective such as cost instead of maximizing a profit function n Minimization problems can be solved graphically by first setting up the feasible solution region and then using either the corner point method or an isocost line approach (which is analogous to the isoprofit approach in maximization problems) to find the values of the decision variables (e. g. , X 1 and X 2) that yield the minimum cost © 2009 Prentice-Hall, Inc. 7 – 43

Holiday Meal Turkey Ranch n The Holiday Meal Turkey Ranch is considering buying two different brands of turkey feed and blending them to provide a good, low-cost diet for its turkeys Let X 1 = number of pounds of brand 1 feed purchased X 2 = number of pounds of brand 2 feed purchased Minimize cost (in cents) = 2 X 1 + 3 X 2 subject to: 5 X 1 + 10 X 2≥ 90 ounces (ingredient constraint A) 4 X 1 + 3 X 2≥ 48 ounces (ingredient constraint B) 0. 5 X 1 ≥ 1. 5 ounces (ingredient constraint C) X 1 ≥ 0 (nonnegativity constraint) X 2 ≥ 0 (nonnegativity constraint) © 2009 Prentice-Hall, Inc. 7 – 44

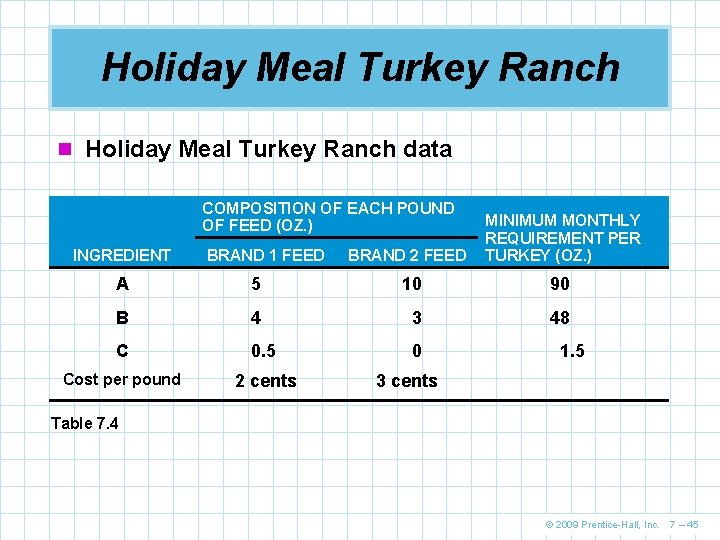
Holiday Meal Turkey Ranch n Holiday Meal Turkey Ranch data COMPOSITION OF EACH POUND OF FEED (OZ. ) INGREDIENT BRAND 1 FEED BRAND 2 FEED MINIMUM MONTHLY REQUIREMENT PER TURKEY (OZ. ) A 5 10 90 B 4 3 48 C 0. 5 0 Cost per pound 2 cents 1. 5 3 cents Table 7. 4 © 2009 Prentice-Hall, Inc. 7 – 45

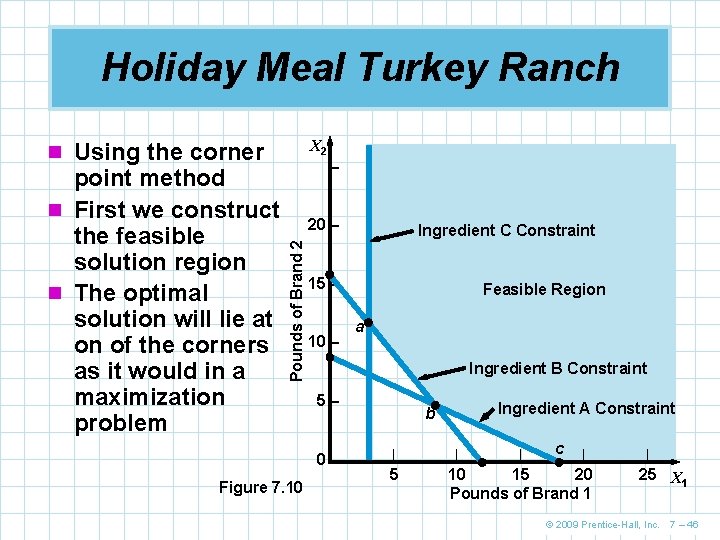
Holiday Meal Turkey Ranch X 2 n Using the corner 20 – Pounds of Brand 2 point method n First we construct the feasible solution region n The optimal solution will lie at on of the corners as it would in a maximization problem – 15 – 10 – Feasible Region a Ingredient B Constraint 5– 0 |– Figure 7. 10 Ingredient C Constraint Ingredient A Constraint b | 5 | | c | 10 15 20 Pounds of Brand 1 | 25 X 1 © 2009 Prentice-Hall, Inc. 7 – 46

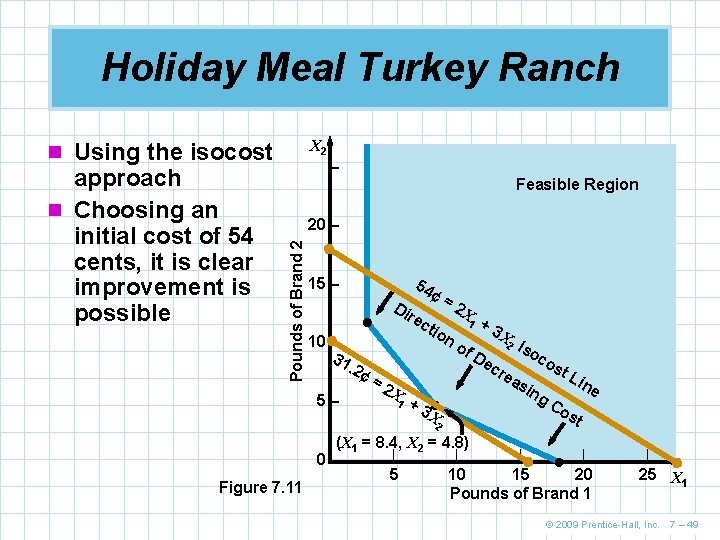
Holiday Meal Turkey Ranch n We solve for the values of the three corner points n Point a is the intersection of ingredient constraints C and B 4 X 1 + 3 X 2 = 48 X 1 = 3 n Substituting 3 in the first equation, we find X 2 = 12 n Solving for point b with basic algebra we find X 1 = 8. 4 and X 2 = 4. 8 n Solving for point c we find X 1 = 18 and X 2 = 0 © 2009 Prentice-Hall, Inc. 7 – 47

Holiday Meal Turkey Ranch n Substituting these value back into the objective function we find Cost = 2 X 1 + 3 X 2 Cost at point a = 2(3) + 3(12) = 42 Cost at point b = 2(8. 4) + 3(4. 8) = 31. 2 Cost at point c = 2(18) + 3(0) = 36 n The lowest cost solution is to purchase 8. 4 pounds of brand 1 feed and 4. 8 pounds of brand 2 feed for a total cost of 31. 2 cents per turkey © 2009 Prentice-Hall, Inc. 7 – 48

Holiday Meal Turkey Ranch X 2 n Using the isocost Feasible Region 20 – Pounds of Brand 2 approach n Choosing an initial cost of 54 cents, it is clear improvement is possible – 15 – Di 54 re 10 – 31. 2¢ 5– =2 X 1 ¢= cti +3 on 2 X 1 of +3 X 2 De cr Iso co ea sin os X (X 1 = 8. 4, X 2 = 4. 8) Figure 7. 11 | 5 ine g. C 2 0 |– st L | | t | 10 15 20 Pounds of Brand 1 | 25 X 1 © 2009 Prentice-Hall, Inc. 7 – 49

Holiday Meal Turkey Ranch n QM for Windows can also be used to solve the Holiday Meal Turkey Ranch problem Program 7. 3 © 2009 Prentice-Hall, Inc. 7 – 50

Employee Scheduling Applications n Assignment Problems n Involve determining the most efficient way to assign resources to tasks n Objective may be to minimize travel times or maximize assignment effectiveness n Assignment problems are unique because they have a coefficient of 0 or 1 associated with each variable in the LP constraints and the right-hand side of each constraint is always equal to 1 © 2009 Prentice-Hall, Inc. 7 – 51

Employee Scheduling Applications n Ivan and Ivan law firm maintains a large staff of n n n young attorneys Ivan wants to make lawyer-to-client assignments in the most effective manner He identifies four lawyers who could possibly be assigned new cases Each lawyer can handle one new client The lawyers have different skills and special interests The following table summarizes the lawyers estimated effectiveness on new cases © 2009 Prentice-Hall, Inc. 7 – 52

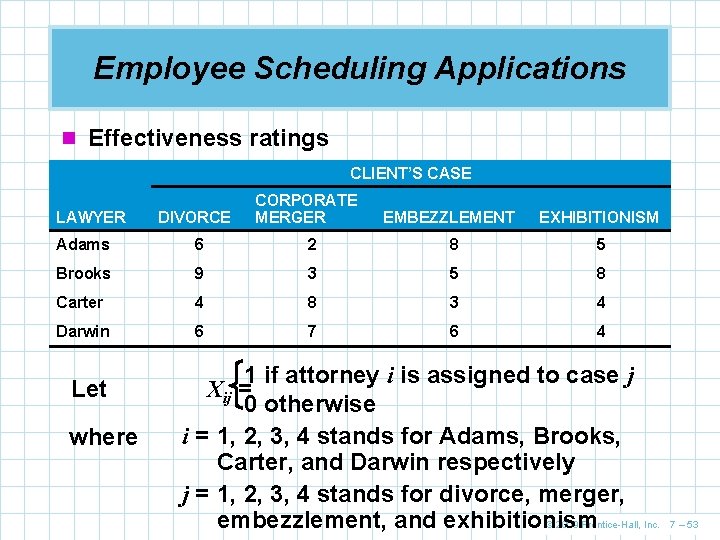
Employee Scheduling Applications n Effectiveness ratings CLIENT’S CASE LAWYER DIVORCE CORPORATE MERGER EMBEZZLEMENT EXHIBITIONISM Adams 6 2 8 5 Brooks 9 3 5 8 Carter 4 8 3 4 Darwin 6 7 6 4 Let where 1 if attorney i is assigned to case j Xij = 0 otherwise i = 1, 2, 3, 4 stands for Adams, Brooks, Carter, and Darwin respectively j = 1, 2, 3, 4 stands for divorce, merger, embezzlement, and exhibitionism © 2009 Prentice-Hall, Inc. 7 – 53

Employee Scheduling Applications n The LP formulation is Maximize effectiveness 6 X= 11 + 2 X 12 + 8 X 13 + 5 X 14 + 9 X 21 + 3 X 22 + 5 X 23 + 8 X 24 + 4 X 31 + 8 X 32 + 3 X 33 + 4 X + 6 X 41 + 7 X 42 + 6 X 43 + 4 X 44 subject to X 11 + X 21 + X 31 + X 41 = 1 X 12 + X 22 + X 32 + X 42 = 1 X 13 + X 23 + X 33 + X 43 = 1 X 14 + X 24 + X 34 + X 44 = 1 X 11 + X 12 + X 13 + X 14 = 1 X 21 + X 22 + X 23 + X 24 = 1 X 31 + X 32 + X 33 + X 34 = 1 X 41 + X 42 + X 43 + X 44 = 1 (divorce case) (merger) (embezzlement) (exhibitionism) (Adams) (Brook) (Carter) (Darwin) © 2009 Prentice-Hall, Inc. 7 – 54

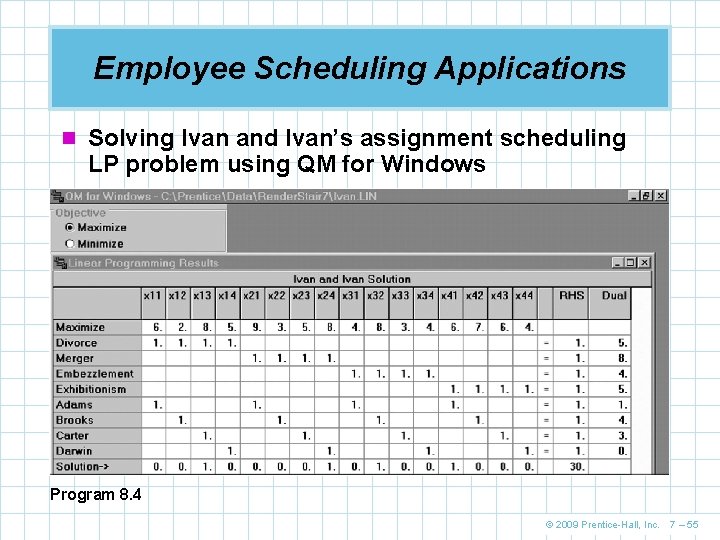
Employee Scheduling Applications n Solving Ivan and Ivan’s assignment scheduling LP problem using QM for Windows Program 8. 4 © 2009 Prentice-Hall, Inc. 7 – 55

Four Special Cases in LP n Four special cases and difficulties arise at times when using the graphical approach to solving LP problems n Infeasibility n Unboundedness n Redundancy n Alternate Optimal Solutions © 2009 Prentice-Hall, Inc. 7 – 56

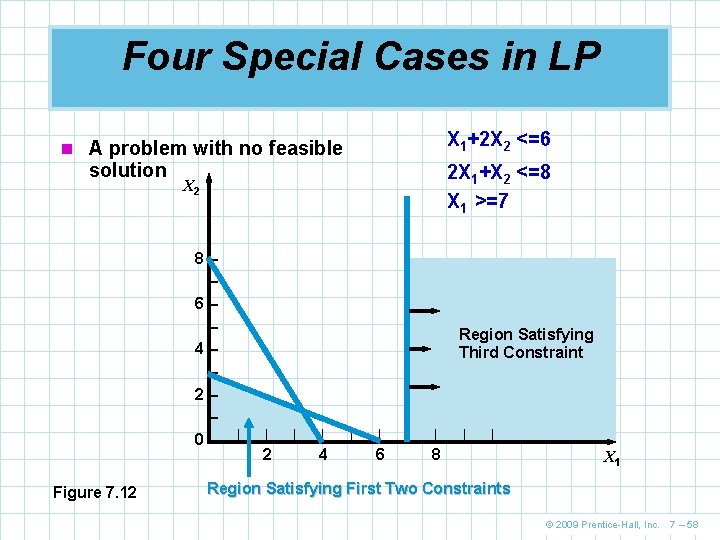
Four Special Cases in LP n No feasible solution n Exists when there is no solution to the problem that satisfies all the constraint equations n No feasible solution region exists n This is a common occurrence in the real world n Generally one or more constraints are relaxed until a solution is found © 2009 Prentice-Hall, Inc. 7 – 57

Four Special Cases in LP X 1+2 X 2 <=6 n A problem with no feasible solution 2 X 1+X 2 <=8 X 1 >=7 X 2 8– – 6– – 4– – 2– – 0– Figure 7. 12 Region Satisfying Third Constraint | | 2 | | 4 | | 6 | | 8 X 1 Region Satisfying First Two Constraints © 2009 Prentice-Hall, Inc. 7 – 58

Four Special Cases in LP n Unboundedness n Sometimes a linear program will not have a finite solution n In a maximization problem, one or more solution variables, and the profit, can be made infinitely large without violating any constraints n In a graphical solution, the feasible region will be open ended n This usually means the problem has been formulated improperly © 2009 Prentice-Hall, Inc. 7 – 59

Four Special Cases in LP n A solution region unbounded to the right X 2 X 1 ≥ 5 15 – X 2 ≤ 10 10 – Feasible Region 5– X 1 + 2 X 2 ≥ 15 0 |– | | | 5 10 15 | X 1 Figure 7. 13 © 2009 Prentice-Hall, Inc. 7 – 60

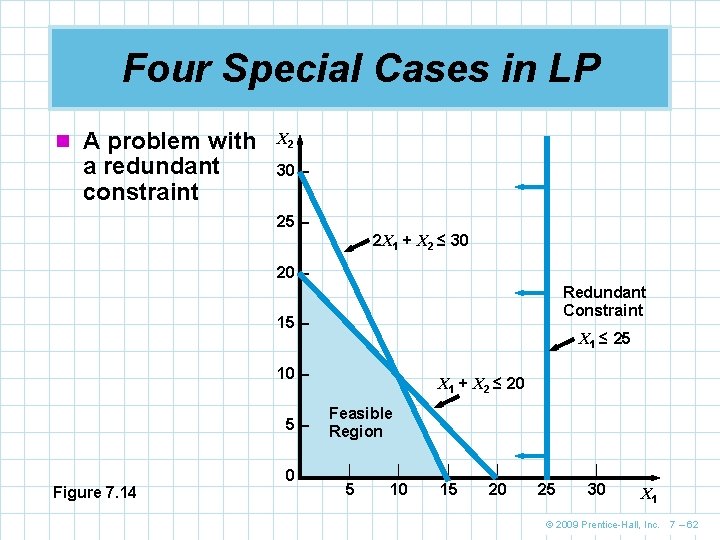
Four Special Cases in LP n Redundancy n A redundant constraint is one that does not affect the feasible solution region n One or more constraints may be more binding n This is a very common occurrence in the real world n It causes no particular problems, but eliminating redundant constraints simplifies the model © 2009 Prentice-Hall, Inc. 7 – 61

Four Special Cases in LP n A problem with a redundant constraint X 2 30 – 25 – 2 X 1 + X 2 ≤ 30 20 – Redundant Constraint 15 – X 1 ≤ 25 10 – 5– Figure 7. 14 0– X 1 + X 2 ≤ 20 Feasible Region | | | 5 10 15 20 25 30 X 1 © 2009 Prentice-Hall, Inc. 7 – 62

Four Special Cases in LP n Alternate Optimal Solutions n Occasionally two or more optimal solutions may exist n Graphically this occurs when the objective function’s isoprofit or isocost line runs perfectly parallel to one of the constraints n This actually allows management great flexibility in deciding which combination to select as the profit is the same at each alternate solution © 2009 Prentice-Hall, Inc. 7 – 63

Four Special Cases in LP n Example of alternate optimal solutions X 2 8– 7– A 6– Maximize 3 X 1 + 2 X 2 Subj. To: 6 X 1 + 4 X 2 < 24 X 1 <3 X 1 , X 2 > 0 5– Optimal Solution Consists of All Combinations of X 1 and X 2 Along the AB Segment 4– 3– Isoprofit Line for $8 2– Figure 7. 15 1 – Feasible Region | | 0– 1 2 B Isoprofit Line for $12 Overlays Line Segment AB | | | 3 4 5 6 7 8 X 1 © 2009 Prentice-Hall, Inc. 7 – 64

Sensitivity Analysis n Optimal solutions to LP problems thus far have n n been found under what are called deterministic assumptions This means that we assume complete certainty in the data and relationships of a problem But in the real world, conditions are dynamic and changing We can analyze how sensitive a deterministic solution is to changes in the assumptions of the model This is called sensitivity analysis, analysis postoptimality analysis, analysis parametric programming, programming or optimality analysis © 2009 Prentice-Hall, Inc. 7 – 65

Sensitivity Analysis n Sensitivity analysis often involves a series of what -if? questions concerning constraints, variable coefficients, and the objective function n n What if the profit for product 1 increases by 10%? What if less advertising money is available? n One way to do this is the trial-and-error method where values are changed and the entire model is resolved n The preferred way is to use an analytic postoptimality analysis n After a problem has been solved, we determine a range of changes in problem parameters that will not affect the optimal solution or change the variables in the solution without re-solving the entire problem © 2009 Prentice-Hall, Inc. 7 – 66

Sensitivity Analysis n Sensitivity analysis can be used to deal not only with errors in estimating input parameters to the LP model but also with management’s experiments with possible future changes in the firm that may affect profits. © 2009 Prentice-Hall, Inc. 7 – 67

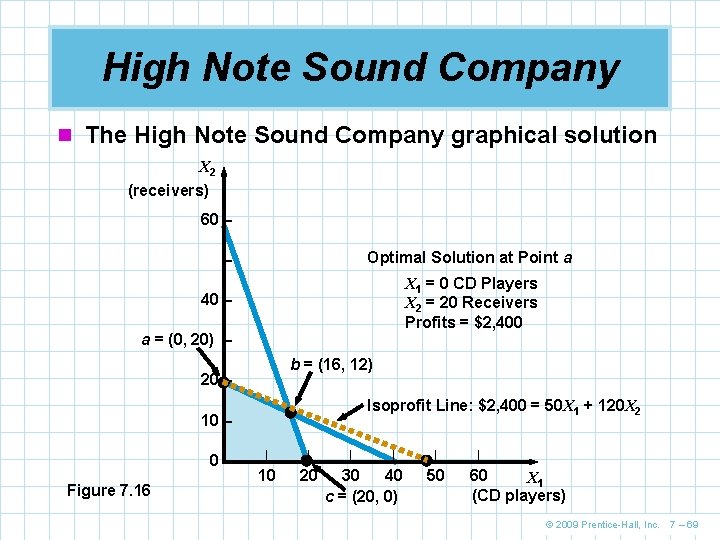
High Note Sound Company n The High Note Sound Company manufactures quality CD players and stereo receivers n Products require a certain amount of skilled artisanship which is in limited supply n The firm has formulated the following product mix LP model Maximize profit = $50 X 1 + $120 X 2 Subject to 2 X 1 + 4 X 2 ≤ 80 3 X 1 + 1 X 2 ≤ 60 (hours of electrician’s time available) (hours of audio technician’s time available) X 1 , X 2 ≥ 0 © 2009 Prentice-Hall, Inc. 7 – 68

High Note Sound Company n The High Note Sound Company graphical solution X 2 (receivers) 60 – Optimal Solution at Point a – X 1 = 0 CD Players X 2 = 20 Receivers Profits = $2, 400 40 – a = (0, 20) – b = (16, 12) 20 – Isoprofit Line: $2, 400 = 50 X 1 + 120 X 2 10 – 0– Figure 7. 16 | | 10 20 | | 30 40 c = (20, 0) | 50 | 60 X 1 (CD players) © 2009 Prentice-Hall, Inc. 7 – 69

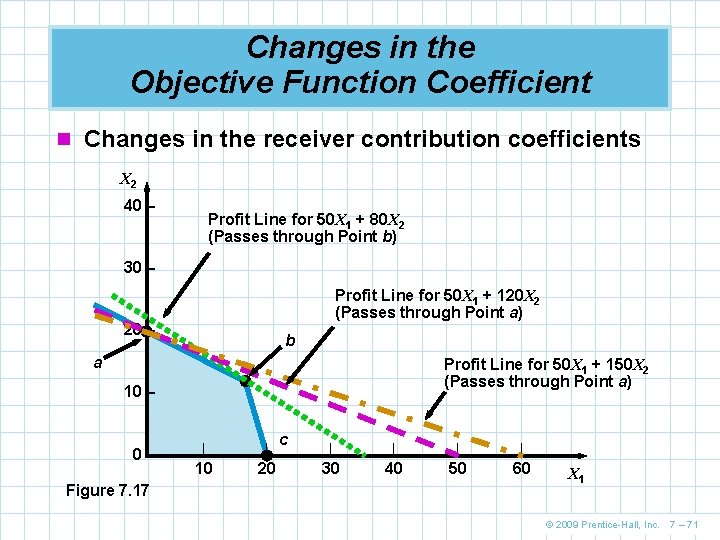
Changes in the Objective Function Coefficient n In real-life problems, contribution rates in the objective functions fluctuate periodically n Graphically, this means that although the feasible solution region remains exactly the same, the slope of the isoprofit or isocost line will change n We can often make modest increases or decreases in the objective function coefficient of any variable without changing the current optimal corner point n We need to know how much an objective function coefficient can change before the optimal solution would be at a different corner point © 2009 Prentice-Hall, Inc. 7 – 70

Changes in the Objective Function Coefficient n Changes in the receiver contribution coefficients X 2 40 – Profit Line for 50 X 1 + 80 X 2 (Passes through Point b) 30 – Profit Line for 50 X 1 + 120 X 2 (Passes through Point a) 20 – b a Profit Line for 50 X 1 + 150 X 2 (Passes through Point a) 10 – 0– Figure 7. 17 | | 10 20 c | | 30 40 50 60 X 1 © 2009 Prentice-Hall, Inc. 7 – 71

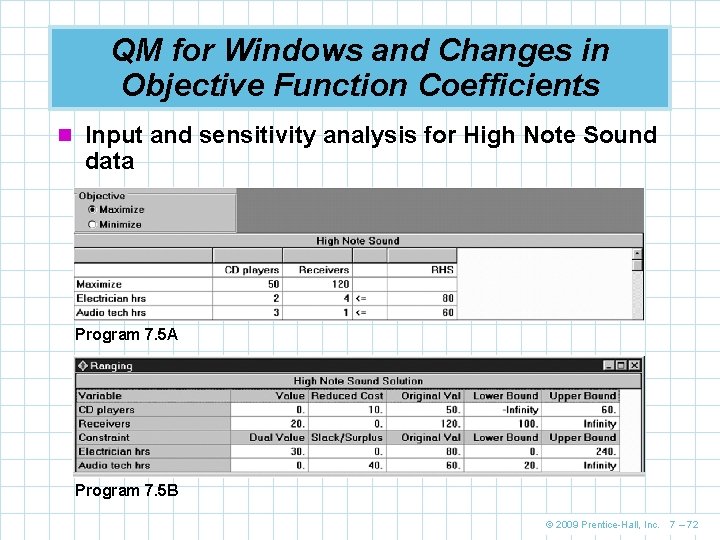
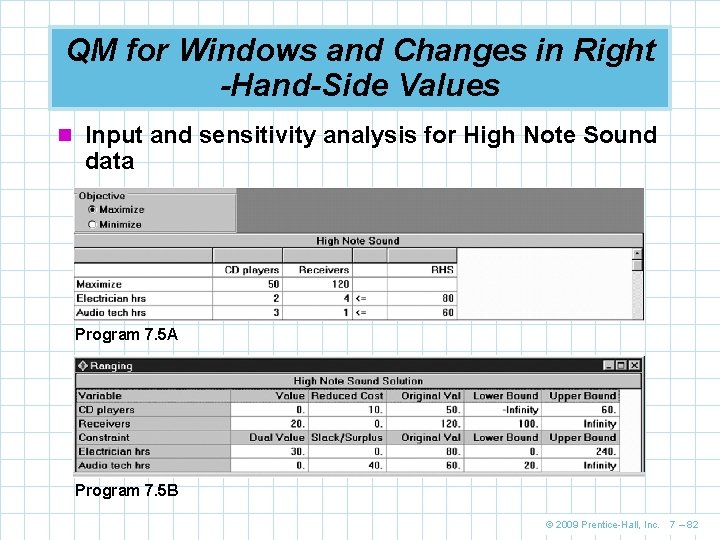
QM for Windows and Changes in Objective Function Coefficients n Input and sensitivity analysis for High Note Sound data Program 7. 5 A Program 7. 5 B © 2009 Prentice-Hall, Inc. 7 – 72

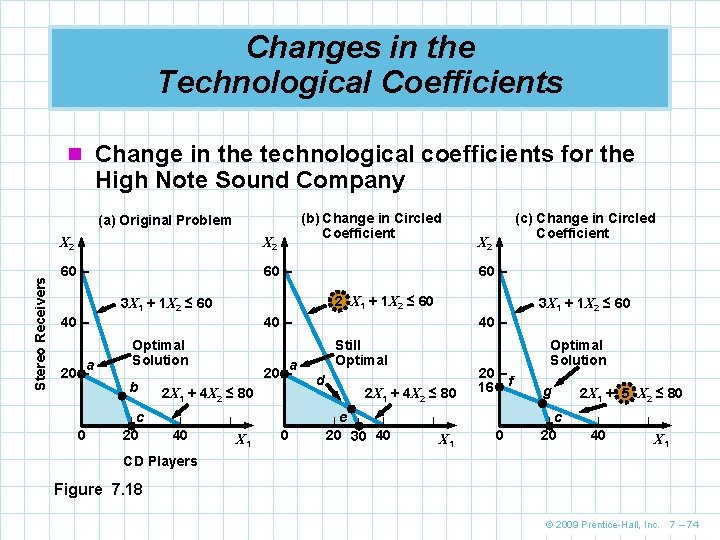
Changes in the Technological Coefficients n Changes in the technological coefficients often reflect changes in the state of technology n If the amount of resources needed to produce a product changes, coefficients in the constraint equations will change n This does not change the objective function, but it can produce a significant change in the shape of the feasible region n This may cause a change in the optimal solution © 2009 Prentice-Hall, Inc. 7 – 73

Changes in the Technological Coefficients n Change in the technological coefficients for the High Note Sound Company (b) Change in Circled Coefficient Stereo Receivers (a) Original Problem X 2 60 – 2 X 1 + 1 X 2 ≤ 60 40 – – 0 3 X 1 + 1 X 2 ≤ 60 40 – Optimal Solution b c 20 | a 20 – 2 X 1 + 4 X 2 ≤ 80 | 40 X 2 60 – 3 X 1 + 1 X 2 ≤ 60 a 20 – (c) Change in Circled Coefficient | X 1 – 0 40 – Still Optimal d 2 X 1 + 4 X 2 ≤ 80 e | | 20 30 40 | | X 1 20 – 16 f – 0 Optimal Solution g c 20 | 2 X 1 + 5 X 2 ≤ 80 | 40 | X 1 CD Players Figure 7. 18 © 2009 Prentice-Hall, Inc. 7 – 74

Changes in Resources or Right -Hand-Side Values n The right-hand-side values of the constraints often represent resources available to the firm n If additional resources were available, a higher total profit could be realized n Sensitivity analysis about resources will help answer questions such as: n How much should the company be willing to pay for additional hours? n Is it profitable to have some electricians work overtime? n Should we be willing to pay for more audio technician time? © 2009 Prentice-Hall, Inc. 7 – 75

Changes in Resources or Right -Hand-Side Values n If the right-hand side of a constraint is changed, the feasible region will change (unless the constraint is redundant) and often the optimal solution will change n The amount of change (increase or decrease) in the objective function value that results from a unit change in one of the resources available is called the dual price or dual value © 2009 Prentice-Hall, Inc. 7 – 76

Changes in Resources or Right -Hand-Side Values n However, the amount of possible increase in the right-hand side of a resource is limited n If the number of hours increases beyond the upper bound (or decreases below the lower bound), then the objective function would no longer increase (decrease) by the dual price. n There may be excess (slack) hours of a resource or the objective function may change by an amount different from the dual price. n Thus, the dual price is relevant only within limits. n If the dual value of a constraint is zero n The slack is positive, indicating unused resource n Additional amount of resource will simply increase the amount of slack. n The upper limit of infinity indicates that adding more hours would simply increase the amount of slack. © 2009 Prentice-Hall, Inc. 7 – 77

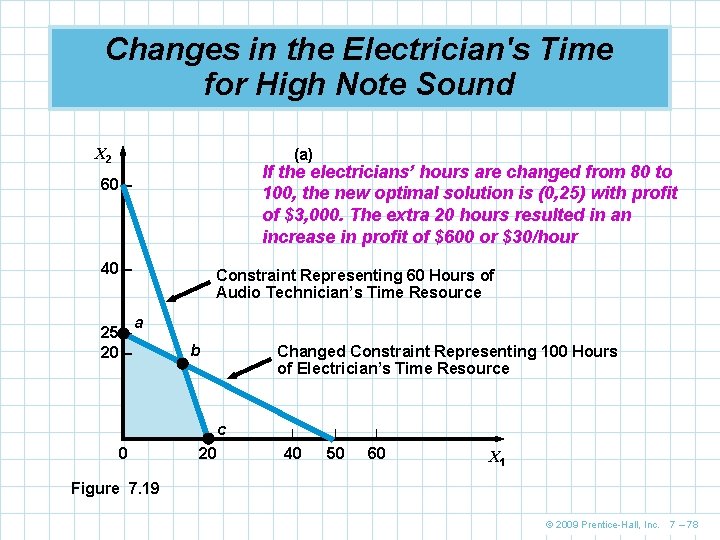
Changes in the Electrician's Time for High Note Sound X 2 (a) If the electricians’ hours are changed from 80 to 100, the new optimal solution is (0, 25) with profit of $3, 000. The extra 20 hours resulted in an increase in profit of $600 or $30/hour 60 – 40 – 25 – 20 – Constraint Representing 60 Hours of Audio Technician’s Time Resource a – 0 b Changed Constraint Representing 100 Hours of Electrician’s Time Resource | 20 c | | | 40 50 60 X 1 Figure 7. 19 © 2009 Prentice-Hall, Inc. 7 – 78

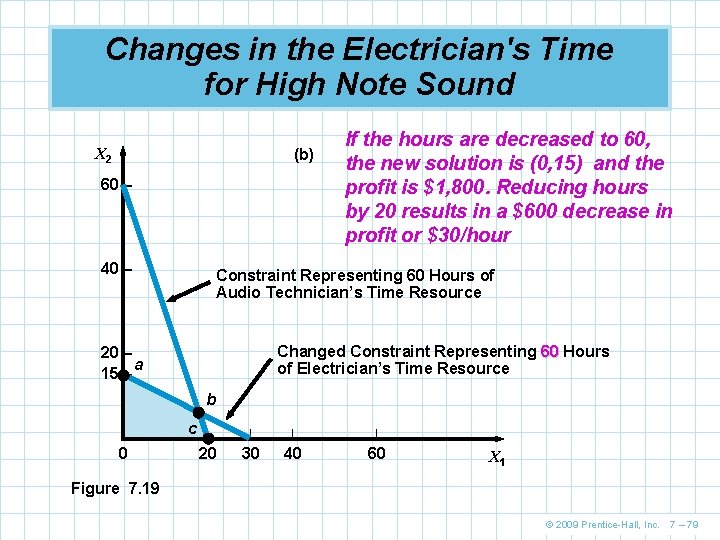
Changes in the Electrician's Time for High Note Sound X 2 (b) 60 – 40 – If the hours are decreased to 60, the new solution is (0, 15) and the profit is $1, 800. Reducing hours by 20 results in a $600 decrease in profit or $30/hour Constraint Representing 60 Hours of Audio Technician’s Time Resource Changed Constraint Representing 60 Hours of Electrician’s Time Resource 20 – a 15 – b – 0 c | | 20 30 40 60 X 1 Figure 7. 19 © 2009 Prentice-Hall, Inc. 7 – 79

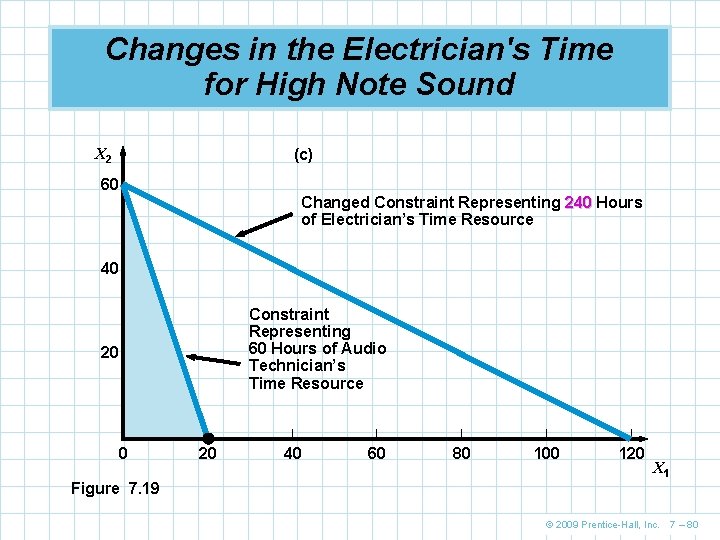
Changes in the Electrician's Time for High Note Sound X 2 (c) 60 – Changed Constraint Representing 240 Hours of Electrician’s Time Resource 40 – Constraint Representing 60 Hours of Audio Technician’s Time Resource 20 – – 0 | | | 20 40 60 80 100 120 X 1 Figure 7. 19 © 2009 Prentice-Hall, Inc. 7 – 80

Changes in the Electrician's Time for High Note Sound n If total electrician time was increased to 240, the optimal solution would be (0, 60) with a profit of $7, 200. This is $2, 400 (the original solution) + $30 (dual price)*160 hours(240 -80) n If the hours increases beyond 240, then the optimal solution would still be (0, 60) and profit would not increase. The extra time is slack during which the electricians are not working © 2009 Prentice-Hall, Inc. 7 – 81

QM for Windows and Changes in Right -Hand-Side Values n Input and sensitivity analysis for High Note Sound data Program 7. 5 A Program 7. 5 B © 2009 Prentice-Hall, Inc. 7 – 82

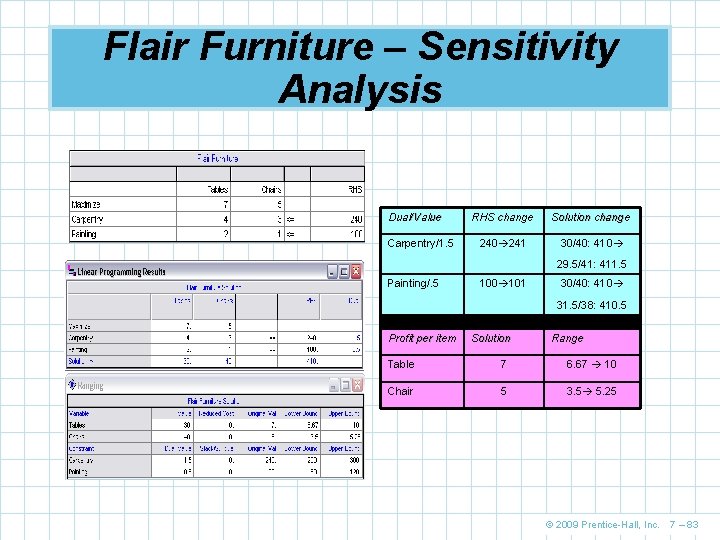
Flair Furniture – Sensitivity Analysis Dual/Value Carpentry/1. 5 RHS change Solution change 240 241 30/40: 410 29. 5/41: 411. 5 Painting/. 5 100 101 30/40: 410 31. 5/38: 410. 5 Profit per item Solution Range Table 7 6. 67 10 Chair 5 3. 5 5. 25 © 2009 Prentice-Hall, Inc. 7 – 83

Personal Mini Warehouses 1. For the optimal solution, how much is spent on 2. 3. 4. 5. advertising? For the optimal solution, how much square footage will be used? Would the solution change if the advertising budget were only $300 instead of $400? Why? What would the optimal solution be if the profit on the large spaces were reduced from $50 to $45? How much would earnings increase if the square footage requirement were increased from 8, 000 to 9, 000? 1. 2*60 + 4*40 = 280 (note slack of 120 on advertising constraint) 2. 100*60 + 50*40 = 8, 000 (no slack) 3. Advertising has a lower bound of 280 and upper bound of Infinity. 300 is within the bounds so the solution does not change. 4. The profit on large spaces has a range of 40 to Infinity, 45 is within that range so the solution would not change. However, earnings would be reduced from $3, 800 to 45*60 + 20*40 = $3, 500. 5. The dual price for square footage is. 4 and the upper bound is 9, 500. By increasing the square footage by 1, 000 we increase the earning by. 4*1, 000 = $400 © 2009 Prentice-Hall, Inc. 7 – 84