Chapter 7 Hypothesis Testing 7 1 Overview 7
































- Slides: 41

Chapter 7 Hypothesis Testing 7 -1 Overview 7 -2 Fundamentals of Hypothesis Testing 7 -3 Testing a Claim about a Mean: Large Samples 7 -4 Testing a Claim about a Mean: Small Samples 7 -5 Testing a Claim about a Proportion 7 -6 Testing a Claim about a Standard Deviation or Variance Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 1

Hypothesis in statistics, is a claim or statement about a property of a population Hypothesis Testing is to test the claim or statement Example: A conjecture is made that “the average starting salary for computer science gradate is $30, 000 per year”. Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 2

Question: How can we justify/test this conjecture? A. What do we need to know to justify this conjecture? B. Based on what we know, how should we justify this conjecture? Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 3

Answer to A: Randomly select, say 100, computer science graduates and find out their annual salaries ---- We need to have some sample observations, i. e. , a sample set! Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 4

Answer to B: That is what we will learn in this chapter ---- Make conclusions based on the sample observations Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 5

Statistical Reasoning Analyze the sample set in an attempt to distinguish between results that can easily occur and results that are highly unlikely. Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 6

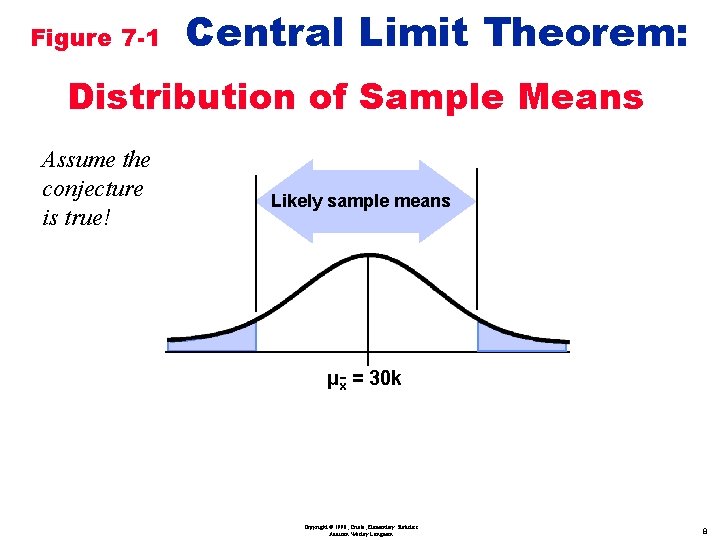
Figure 7 -1 Central Limit Theorem: Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 7

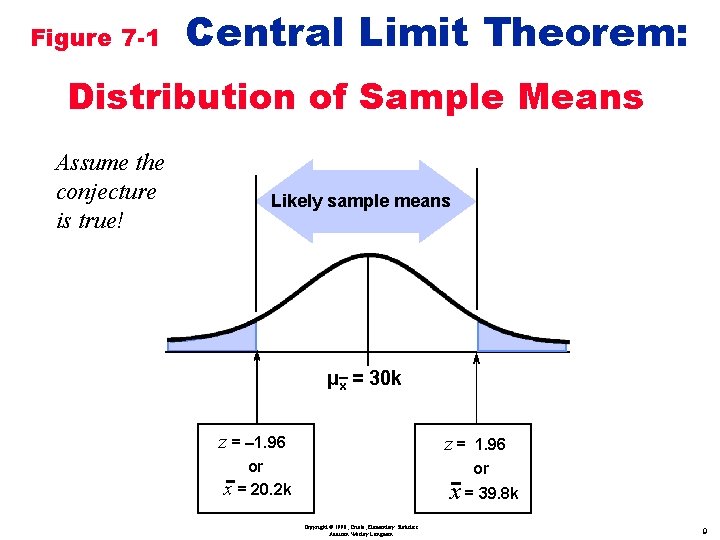
Figure 7 -1 Central Limit Theorem: Distribution of Sample Means Assume the conjecture is true! Likely sample means µx = 30 k Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 8

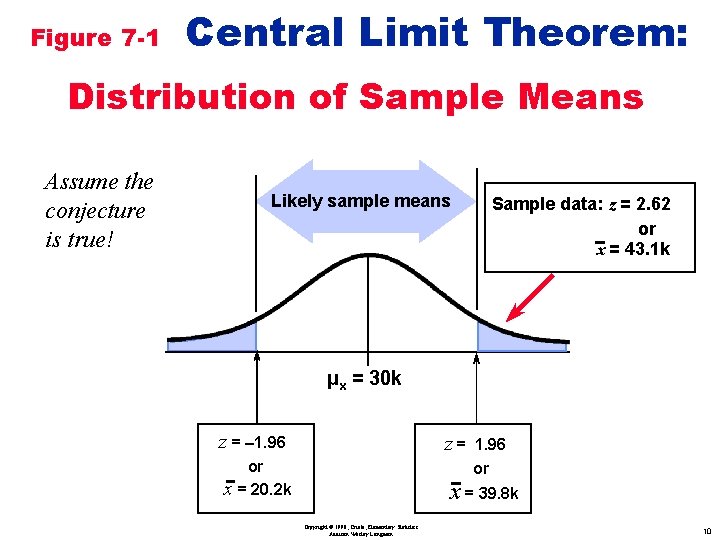
Figure 7 -1 Central Limit Theorem: Distribution of Sample Means Assume the conjecture is true! Likely sample means µx = 30 k z = – 1. 96 z= or x = 20. 2 k 1. 96 or x = 39. 8 k Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 9

Figure 7 -1 Central Limit Theorem: Distribution of Sample Means Assume the conjecture is true! Likely sample means Sample data: z = 2. 62 or x = 43. 1 k µx = 30 k z = – 1. 96 z= or x = 20. 2 k 1. 96 or x = 39. 8 k Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 10

Components of a Formal Hypothesis Test Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 11

Definitions v Null Hypothesis (denoted H 0): is the statement being tested in a test of hypothesis. v Alternative Hypothesis (H 1): is what is believe to be true if the null hypothesis is false. Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 12

Null Hypothesis: H 0 v Must contain condition of equality v =, ³, or £ v Test the Null Hypothesis directly v Reject H 0 or fail to reject H 0 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 13

Alternative Hypothesis: H 1 v Must be true if H 0 is false v ¹, <, > v ‘opposite’ of Null Example: H 0 : µ = 30 versus H 1 : µ > 30 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 14

Stating Your Own Hypothesis v. If you wish to support your claim, the claim must be stated so that it becomes the alternative hypothesis. Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 15

Important Notes: v H 0 must always contain equality; however some claims are not stated using equality. Therefore sometimes the claim and H 0 will not be the same. v. Ideally all claims should be stated that they are Null Hypothesis so that the most serious error would be a Type I error. Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 16

Type I Error v. The mistake of rejecting the null hypothesis when it is true. v. The probability of doing this is called the significance level, denoted by a (alpha). v. Common choices for a: 0. 05 and 0. 01 v. Example: rejecting a perfectly good parachute and refusing to jump Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 17

Type II Error vthe mistake of failing to reject the null hypothesis when it is false. vdenoted by ß (beta) v. Example: failing to reject a defective parachute and jumping out of a plane with it. Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 18

Table 7 -2 Type I and Type II Errors True State of Nature The null hypothesis is true We decide to reject the null hypothesis Type I error (rejecting a true null hypothesis) The null hypothesis is false Correct decision Decision We fail to reject the null hypothesis Correct decision Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman Type II error (failing to reject a false null hypothesis) 19

Definition Test Statistic: is a sample statistic or value based on sample data Example: z= x – µx s/ n Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 20

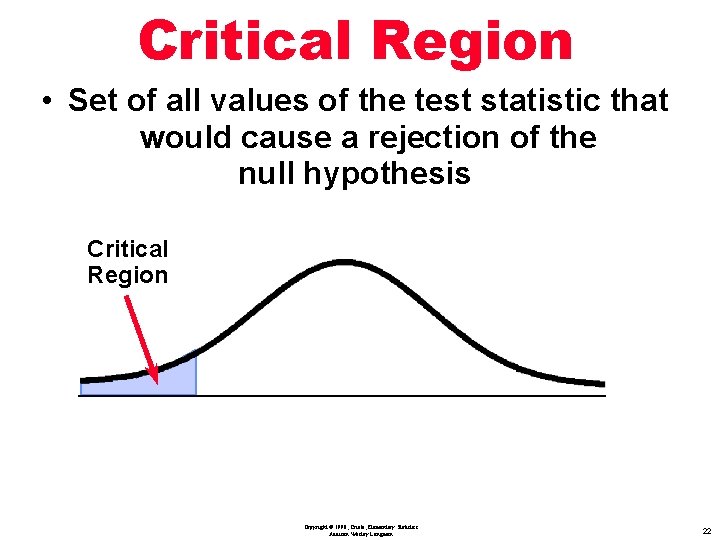
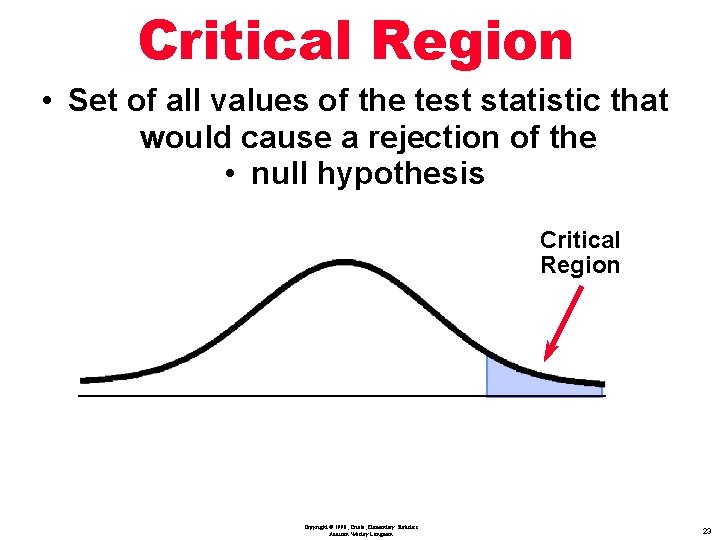
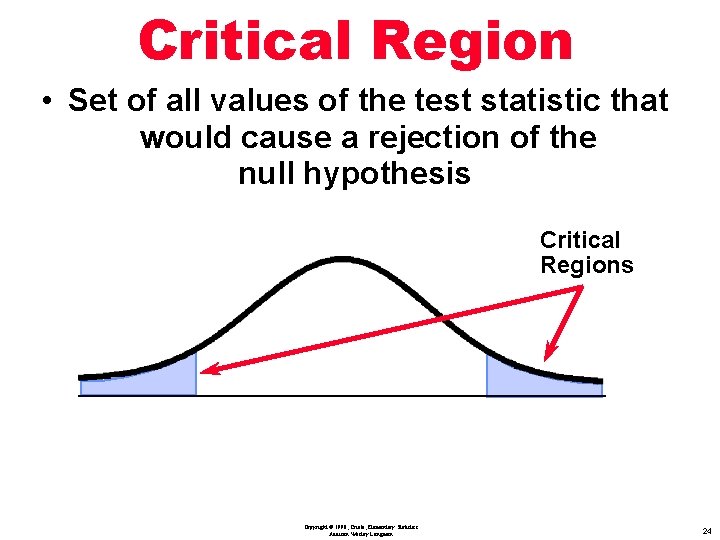
Definition Critical Region : is the set of all values of the test statistic that would cause a rejection of the null hypothesis Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 21

Critical Region • Set of all values of the test statistic that would cause a rejection of the null hypothesis Critical Region Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 22

Critical Region • Set of all values of the test statistic that would cause a rejection of the • null hypothesis Critical Region Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 23

Critical Region • Set of all values of the test statistic that would cause a rejection of the null hypothesis Critical Regions Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 24

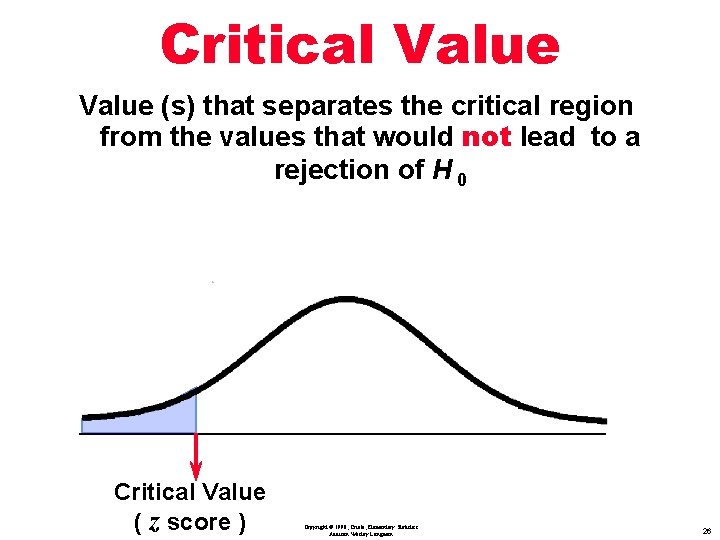
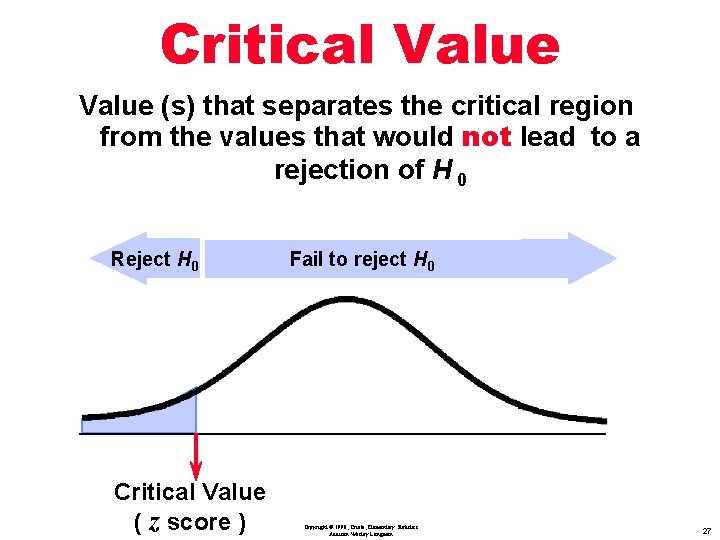
Definition Critical Value: is the value (s) that separates the critical region from the values that would not lead to a rejection of H 0 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 25

Critical Value (s) that separates the critical region from the values that would not lead to a rejection of H 0 Critical Value ( z score ) Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 26

Critical Value (s) that separates the critical region from the values that would not lead to a rejection of H 0 Reject H 0 Critical Value ( z score ) Fail to reject H 0 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 27

Controlling Type I and Type II Errors va, ß, and n are related vwhen two of the three are chosen, the third is determined va and n are usually chosen vtry to use the largest a you can tolerate vif Type I error is serious, select a smaller a value and a larger n value Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 28

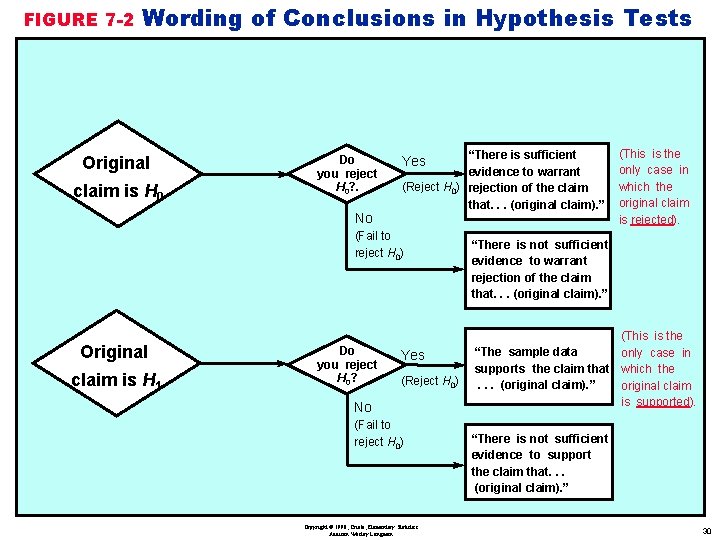
Conclusions in Hypothesis Testing valways test the null hypothesis 1. Fail to reject the H 0 2. Reject the H 0 vneed to formulate correct wording of final conclusion See Figure 7 -2 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 29

FIGURE 7 -2 Wording of Conclusions in Hypothesis Tests Original claim is H 0 Do you reject H 0? . No “There is sufficient evidence to warrant (Reject H 0) rejection of the claim that. . . (original claim). ” Yes (Fail to reject H 0) Original claim is H 1 Do you reject H 0? Yes (Reject H 0) No (Fail to reject H 0) Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman (This is the only case in which the original claim is rejected). “There is not sufficient evidence to warrant rejection of the claim that. . . (original claim). ” (This is the “The sample data only case in supports the claim that which the. . . (original claim). ” original claim is supported). “There is not sufficient evidence to support the claim that. . . (original claim). ” 30

Two-tailed, Left-tailed, Right-tailed Tests Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 31

Left-tailed Test H 0: µ ³ 200 H 1: µ < 200 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 32

Left-tailed Test H 0: µ ³ 200 H 1: µ < 200 Points Left Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 33

Left-tailed Test H 0: µ ³ 200 H 1: µ < 200 Points Left Reject H 0 Values that differ significantly from 200 Fail to reject H 0 200 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 34

Right-tailed Test H 0: µ £ 200 H 1: µ > 200 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 35

Right-tailed Test H 0: µ £ 200 H 1: µ > 200 Points Right Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 36

Right-tailed Test H 0: µ £ 200 H 1: µ > 200 Points Right Fail to reject H 0 Reject H 0 Values that differ significantly from 200 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 37

Two-tailed Test H 0: µ = 200 H 1: µ ¹ 200 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 38

Two-tailed Test H 0: µ = 200 H 1: µ ¹ 200 a is divided equally between the two tails of the critical region Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 39

Two-tailed Test H 0: µ = 200 H 1: µ ¹ 200 a is divided equally between the two tails of the critical region Means less than or greater than Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 40

Two-tailed Test H 0: µ = 200 H 1: µ ¹ 200 a is divided equally between the two tails of the critical region Means less than or greater than Reject H 0 Fail to reject H 0 Reject H 0 200 Values that differ significantly from 200 Copyright © 1998, Triola, Elementary Statistics Addison Wesley Longman 41