Chapter 7 Geometric Inequalities Eleanor Roosevelt High School

Chapter 7 Geometric Inequalities Eleanor Roosevelt High School Geometry Mr. Chin-Sung Lin

ERHS Math Geometry Inequality Postulates Mr. Chin-Sung Lin

ERHS Math Geometry Basic Inequality Postulates Comparison (Whole-Parts) Postulate Transitive Property Substitution Postulate Trichotomy Postulate Mr. Chin-Sung Lin

ERHS Math Geometry Basic Inequality Postulates Addition Postulate Subtraction Postulate Multiplication Postulate Division Postulate Mr. Chin-Sung Lin

ERHS Math Geometry Comparison Postulate A whole is greater than any of its parts If a = b + c and a, b, c > 0 then a > b and a > c Mr. Chin-Sung Lin

ERHS Math Geometry Transitive Property If a, b, and c are real numbers such that a > b and b > c, then a > c Mr. Chin-Sung Lin

ERHS Math Geometry Substitution Postulate A quantity may be substituted for its equal in any statement of inequality If a > b and b = c, then a > c Mr. Chin-Sung Lin

ERHS Math Geometry Trichotomy Postulate Give any two quantities, a and b, one and only one of the following is true: a < b or a = b or a > b Mr. Chin-Sung Lin

ERHS Math Geometry Addition Postulate I If equal quantities are added to unequal quantities, then the sum are unequal in the same order If a > b, then a + c > b + c If a < b, then a + c < b + c Mr. Chin-Sung Lin

ERHS Math Geometry Addition Postulate II If unequal quantities are added to unequal quantities in the same order, then the sum are unequal in the same order If a > b and c > d, then a + c > b + d If a < b and c < d, then a + c < b + d Mr. Chin-Sung Lin

ERHS Math Geometry Subtraction Postulate If equal quantities are subtracted from unequal quantities, then the difference are unequal in the same order If a > b, then a - c > b - c If a < b, then a - c < b - c Mr. Chin-Sung Lin

ERHS Math Geometry Multiplication Postulate I If unequal quantities are multiplied by positive equal quantities, then the products are unequal in the same order c > 0: If a > b, then ac > bc If a < b, then ac < bc Mr. Chin-Sung Lin

ERHS Math Geometry Multiplication Postulate II If unequal quantities are multiplied by negative equal quantities, then the products are unequal in the opposite order c < 0: If a > b, then ac < bc If a < b, then ac > bc Mr. Chin-Sung Lin

ERHS Math Geometry Division Postulate I If unequal quantities are divided by positive equal quantities, then the quotients are unequal in the same order c > 0: If a > b, then a/c > b/c If a < b, then a/c < b/c Mr. Chin-Sung Lin

ERHS Math Geometry Division Postulate II If unequal quantities are divided by negative equal quantities, then the quotients are unequal in the opposite order c < 0: If a > b, then a/c < b/c If a < b, then a/c > b/c Mr. Chin-Sung Lin

ERHS Math Geometry Theorems of Inequality Mr. Chin-Sung Lin

ERHS Math Geometry Theorems of Inequality Exterior Angle Inequality Theorem Triangle Inequality Theorem Greater Angle Theorem Longer Side Theorem Converse of Pythagorean Theorem Mr. Chin-Sung Lin

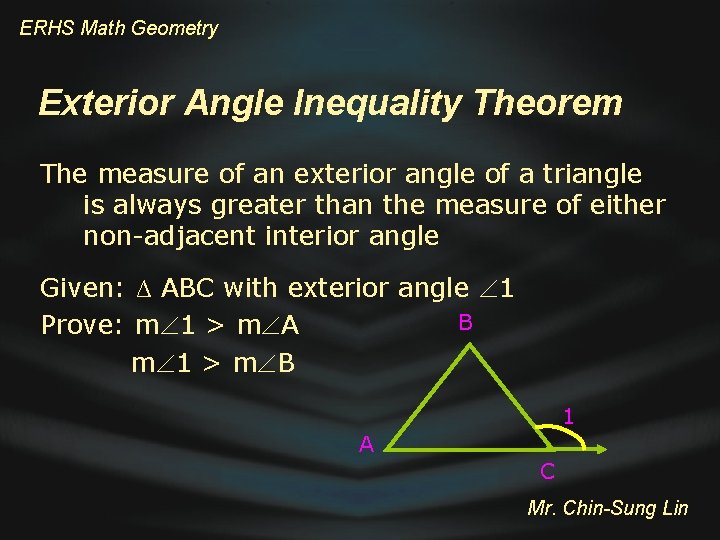
ERHS Math Geometry Exterior Angle Inequality Theorem The measure of an exterior angle of a triangle is always greater than the measure of either non-adjacent interior angle Given: ∆ ABC with exterior angle 1 B Prove: m 1 > m A m 1 > m B 1 A C Mr. Chin-Sung Lin

ERHS Math Geometry Exterior Angle Inequality Theorem B A Statements 1 C Reasons 1. 1 is exterior angle and A & B are remote interior angles 1. Given 2. m 1 = m A +m B 2. Exterior angle theorem 3. m A > 0 and m B > 0 4. m 1 > m A m 1 > m B 3. Definition of triangles 4. Comparison postulate Mr. Chin-Sung Lin

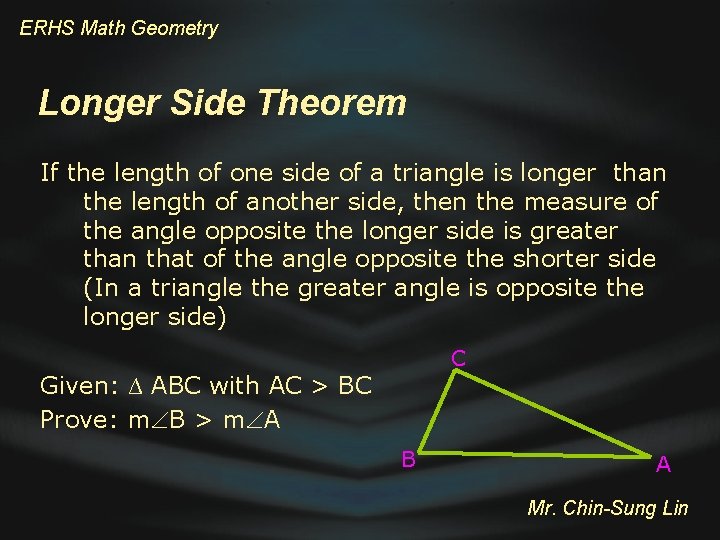
ERHS Math Geometry Longer Side Theorem If the length of one side of a triangle is longer than the length of another side, then the measure of the angle opposite the longer side is greater than that of the angle opposite the shorter side (In a triangle the greater angle is opposite the longer side) C Given: ∆ ABC with AC > BC Prove: m B > m A B A Mr. Chin-Sung Lin

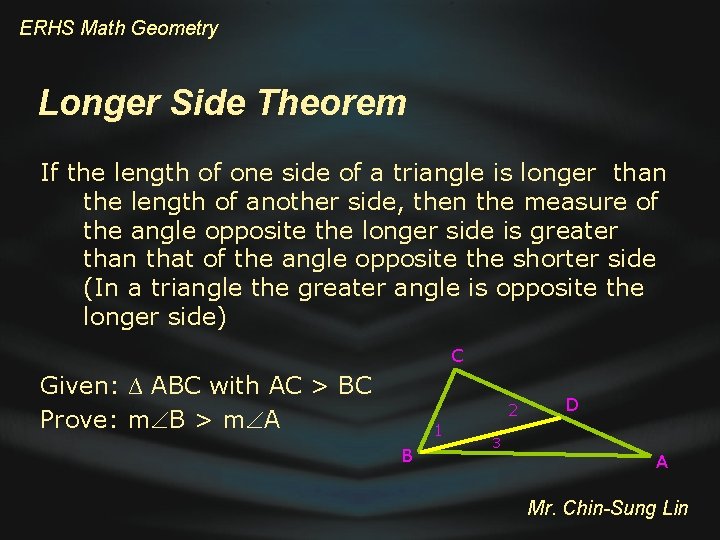
ERHS Math Geometry Longer Side Theorem If the length of one side of a triangle is longer than the length of another side, then the measure of the angle opposite the longer side is greater than that of the angle opposite the shorter side (In a triangle the greater angle is opposite the longer side) C Given: ∆ ABC with AC > BC Prove: m B > m A 2 1 B 3 D A Mr. Chin-Sung Lin

ERHS Math Geometry C Longer Side Theorem Statements 1 B 2 3 D A Reasons 1. AC > BC 1. Given 2. Choose D on AC, CD = BC and 2. Form an isosceles triangle draw a line segment BD 3. m 1 = m 2 4. m 2 > m A 5. 6. 7. 8. m 1 m B m B > = > > m A m 1 + m 3 m 1 m A 3. Base angle theorem 4. Exterior angle is greater than the remote int. angle 5. Substitution postulate 6. Partition property 7. Comparison postulate 8. Transitive property Mr. Chin-Sung Lin

ERHS Math Geometry Greater Angle Theorem If the measure of one angle of a triangle is greater than the measure of another angle, then the side opposite the greater angle is longer than the side opposite the smaller angle (In a triangle the longer side is opposite the greater angle) C Given: ∆ ABC with m B > m A Prove: AC > BC B A Mr. Chin-Sung Lin

ERHS Math Geometry Greater Angle Theorem Statements 1. 2. 3. 4. C B A Reasons m B > m A Assume AC ≤ BC m B = m A (when AC = BC) m B < m A (when AC < BC) 1. Given 2. Assume the opposite is true 3. Base angle theorem 4. Greater angle is opposite the longer side 5. Statement 3 & 4 both contraidt 5. Contradicts to the given statement 1 6. AC > BC 6. The opposite of the assumption is true Mr. Chin-Sung Lin

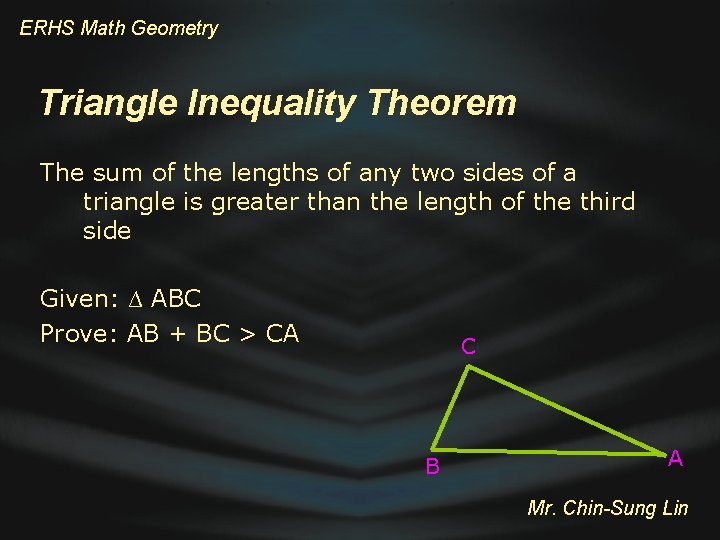
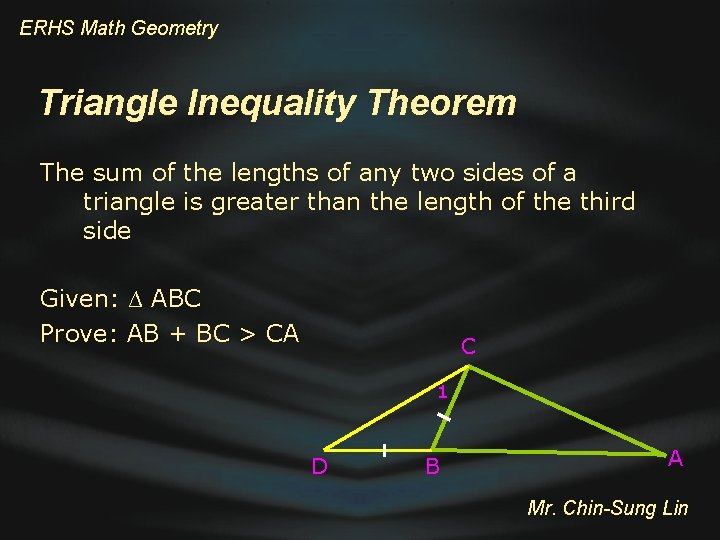
ERHS Math Geometry Triangle Inequality Theorem The sum of the lengths of any two sides of a triangle is greater than the length of the third side Given: ∆ ABC Prove: AB + BC > CA C B A Mr. Chin-Sung Lin

ERHS Math Geometry Triangle Inequality Theorem The sum of the lengths of any two sides of a triangle is greater than the length of the third side Given: ∆ ABC Prove: AB + BC > CA C 1 D B A Mr. Chin-Sung Lin

ERHS Math Geometry Triangle Inequality Theorem C 1 Statements D B 1. Let D on AB and DB = CB, and connect DC 2. m 1 = m D 3. m DCA = m 1 + m C 4. m DCA > m 1 5. m DCA > m D 6. AD > CA 7. AD = AB + BD 8. AB + BD > CA 9. AB + BC > CA A Reasons 1. Form an isosceles triangle 2. Base angle theorem 3. Partition property 4. Comparison postulate 5. Substitution postulate 6. Longer side is opposite the greater angle 7. Partition property 8. Substitution postulate 9. Substitution postulate Mr. Chin-Sung Lin

ERHS Math Geometry Converse of Pythagorean Theorem A corollary of the Pythagorean theorem's converse is a simple means of determining whether a triangle is right, obtuse, or acute Given: ∆ ABC and c is the longest side Prove: If a 2 +b 2 = c 2, then the triangle is right If a 2 + b 2 > c 2, then the triangle is acute If a 2 + b 2 < c 2, then the triangle is obtuse C B A Mr. Chin-Sung Lin

ERHS Math Geometry Triangle Inequality Exercises Mr. Chin-Sung Lin

ERHS Math Geometry Exercise 1 ∆ ABC with AB = 10, BC = 8, find the possible range of CA Mr. Chin-Sung Lin

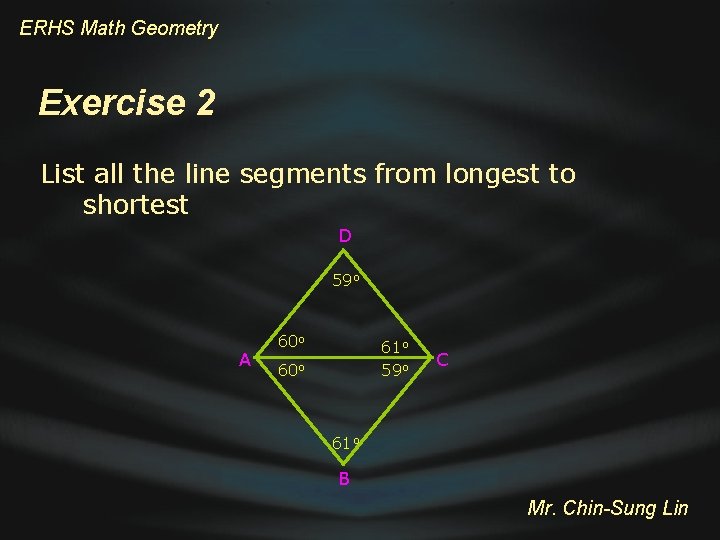
ERHS Math Geometry Exercise 2 List all the line segments from longest to shortest D 59 o A 60 o 61 o 59 o 60 o C 61 o B Mr. Chin-Sung Lin

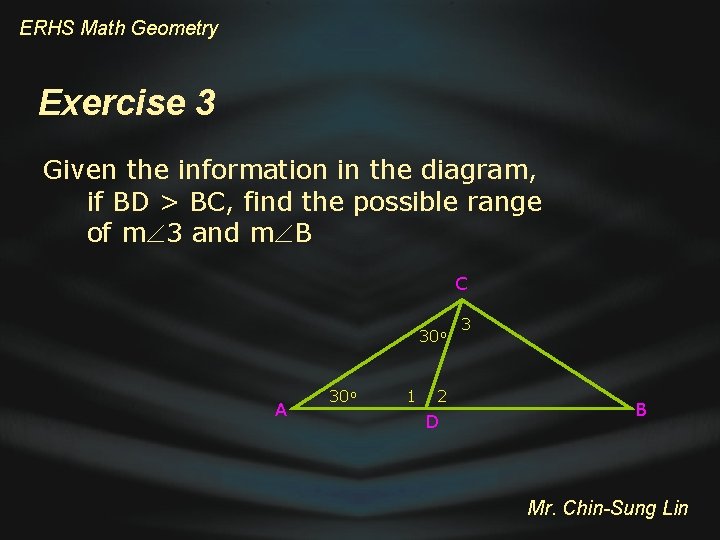
ERHS Math Geometry Exercise 3 Given the information in the diagram, if BD > BC, find the possible range of m 3 and m B C 30 o A 30 o 1 2 D 3 B Mr. Chin-Sung Lin

ERHS Math Geometry Exercise 4 ∆ ABC with AB = 5, BC = 3, CA = 7, (a) what’s the type of ∆ ABC ? (Obtuse ∆? Acute ∆? Right ∆? ) (b) list the angles of the triangle from largest to smallest Mr. Chin-Sung Lin

ERHS Math Geometry Exercise 5 ∆ ABC with AB = 5, BC = 3, (a) if ∆ ABC is a right triangle, find the possible values of CA (b) if ∆ ABC is a obtuse triangle, find the possible range of CA (c) if ∆ ABC is a acute triangle, find the possible range of CA Mr. Chin-Sung Lin

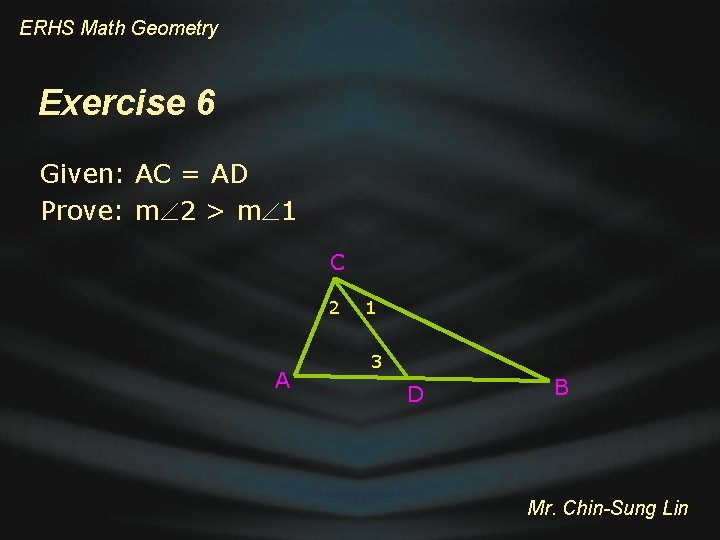
ERHS Math Geometry Exercise 6 Given: AC = AD Prove: m 2 > m 1 C 2 A 1 3 D B Mr. Chin-Sung Lin

ERHS Math Geometry The End Mr. Chin-Sung Lin