Chapter 7 Firstorder logic Propositional logic not expressive

Chapter 7 First-order logic Propositional logic not expressive enough l needs a huge amount of rules l for even for the simple 4 x 4 wumpus world l previous examples on chapter 7 l no power on handling groups of objects l l every object is specified indvidually First-order logic (FOL) l introduces the concepts to overcome that l objects and properties

Why we need logic? Natural language? the expressive power – high but ambiguous l can it be used as a representation language l l l in AI? serves as a medium of communication rather than pure representation l since 1 syntax too many (hidden) semantics l For logic? l it’s like a function: one-to-one mapping.

New concepts Relations l l are the links among objects can be functions – only one output for a given input Examples: l l Objects: people, houses, number, colors, baseball, centuries Relations: either unary (property) or n-ary l l l unary: tall, large, small, red, round, prime, boring n-ary: brother of, greater than, part of, inside, after, is Functions: father of, best friend, one more than

Almost any fact (assertion) can be thought of a combination of objects l and properties or relations l “One plus two equals three” Objects: one, two, three, one plus two l Relation: equals l Function: plus l A name of the object obtained by applying the function plus to the objects one and two

“Squares neighboring the wumpus are smelly. ” Objects: Squares, wumpus Not a function because l Property: smelly many squares may satisfy l Relation: neighboring the constraints, but there l is only one three FOL is important almost any of our concept/knowledge l can be expressed as FOL l

Pros & Cons of FOL Drawback l first-order logic doesn't have things Categories / Classification l Time (Temporal Logic) l Events l Advantage l it can express l l anything that can be programmed Prolog

Difference of FOL and PL PL consider the facts: True or False l use compositionality to see l l whether the sentence is true or false FOL l consider the RELATIONS with OBJECTS: l l True or False also use compositionality

Models for FOL What is a model? in PL: A B => C l then how many possible combinations? l l l this set of truth values = a model for this world only True or False exists in FOL, a model contains more. objects l domain of an FOL model l l = set of objects (domain elements) it contains

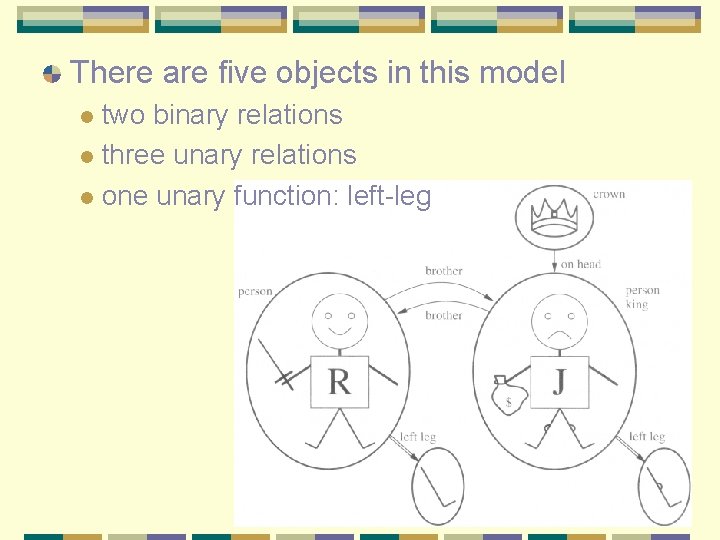
There are five objects in this model two binary relations l three unary relations l one unary function: left-leg l

Formally speaking, relation is l l a set of tuples of objects that are related e. g. , for relation brother, it is the set l { < Richard, King John>, <King John, Richard>} Strictly speaking, l l the functions used in FOL must be total functions i. e. , a function returns a value for every input tuple l l l constituted by the domain elements e. g. , brother: X Y, any body must have a brother? left_leg: X Y, anything must have a left leg? l left_leg(Leftleg 1) = Leftleg 2?

Syntax of FOL

Terms a logical expression of objects l Terms = l constant symbols (1, a, b, peter) l variables (X, Y, Human) l and function symbols (fatherof(peter), plus(1, 2)) l Atomic sentences l the facts in Prolog = Predicate symbol + Terms l = Relation + Objects l e. g. , brother(Richard, John). l married(Father(Richard), Mother(John)) l

Complex sentences multiple atomic sentences combined with logical connectives l Example: l Brother(Richard, John) Brother(John, Richard) l Older(John, 30) Younger(John, 30) l

Quantifiers l For expressing properties of l entire collection of objects – projection of a subset Universal quantification ( ) l Meaning all, l l reading as “For all” Example: “All Kings are Persons” x King(x) Person(x) If X is a King, then X is a Person • called a variable, • lowercase • if it’s a constant, • ground term

Here x King(x) Person(x) is true if x = any domain element, l and the sentence is still true. l x Richard l x King John l x Richard’s left leg l x John’s left leg l x the crown l the above list is called the extended interpretation l By applying this list, what we have? l

Are they true in the model? Yes!!!! (but only for interpretation) from the table of implication ( =>) l whenever the premise is false l l the result is true, regardless of the conclusion So, Universal quantifier l asserts a list of sentences (reduce our work!)

Existential quantification ( ) l Meaning some l l reading as “There exist” or “For some” Example l x Crown(x) On. Head(x, John)

Here, we can see => is the natural connective with l while with l if with , too strong, if => with , too weak

Nested Quantifiers When using multiple quantifiers, e. g. , x y Brother(x, y) => Sibling (x, y) l we can write x, y instead of separate ones l x y Loves (x, y) meaning? l Everybody x loves somebody y l then y x Loves (x, y)? l any difference? l

Somebody y, whom is loved by everybody x. Problem? Quantifiers are not commutative l The order cannot be interchanged l Similar to a query l If we want to specify the precedence, we should use ( ) l e. g. , y ( x Loves (x, y) ) l

Connections between and is a conjunction over the universe While is a disjunction l De Morgan rules can apply to them: l x P x P l x P x P l x P x P So, only one of the or is necessary l we don’t need both

Equality is represented as “=” l instead of a predicate l Example: Father. Of(John) = Henry l To ensure two objects are not the same negation with equality is used l E. g. , x, y Sister(Felix, x) Sister(Felix, y) (x = y) l without that, what is the meaning?

The uniqueness quantifier ! just specifies l One or more different objects ! is used to specify l a unique one object Example: “There is only one king” !x King(x) l Or x King(x) y King(y) (x = y) l l If X is a King & Y is a King then X must be Y

Using first-order logic domain a section of the world l about which we wish to express some knowledge l database, networking, architecture, etc. l The followings are the examples The kinship domain l The domain of numbers, sets and lists l

The kinship domain Also called family relationships domain The objects in the domain are people l The properties of the objects include l Gender l Age l Height, … l l The relations are: l parenthood, brotherhood, marriage, …

Some Examples m, c Mother(c)=m Female(m) Parent(m, c) l w, h Husband(h, w) Male(h) Spouse(h, w) l Disjoint categories: l l l x Male(x) Female(x) Inverse relations: l p, c Parent(p, c) Child(c, p) g, c Grandparent(g, c) p Parent(g, p) Parent(p, c) l x, y Sibling(x, y) x≠y p Parent(p, x) Parent(p, y) we can have many more axioms like these. l this will be one of your exercises in PJ. 3 l

Must the Male, Female, Parent be the set of primitive predicates? l Of course, not. l We may use other predicates as the primitive set l And also, in some domains l we have no clearly identifiable basic set

The domain of numbers Here is theory of natural numbers l to check if a number is natural l l Nat. Num a constant symbol (basis) l 0 a function symbol S, meaning successor Nat. Num(0). l n Nat. Num(n) => Nat. Num(S(n)).

After that, we define constraints about the function S n 0 ≠ S(n) m, n m ≠ n => S(m) ≠ S(n) addition of natural numbers m Nat. Num(m) => ( + (m, 0) = m ) m, n Nat. Num(m) Nat. Num(n) => +(S(m) , n) = S(+(m, n))

The domain of sets We want to represent individual sets, including empty set. What we need? l a way to building up a set by adding an element to a set (adjoining) l take union of two sets l take intersection of two sets l l Checking? membership of an element l whether it is a set or other objects l

Hence we want to define the followings Constant symbol: l {} Predicates: l Set, Member, Subset Functions: l Adjoining, Union, Intersection

The domain of lists Lists are similar to sets l difference? Lists are ordered l An element can appear more than once l l Here is the summary of their difference

Ø ={ } [] = Nil {x} = {x | { } } [x] = Cons(x, Nil) {x, y} = {x | {y | { } } } [x, y] = Cons(x, Cons(y, Nil)) {x, y|s} = {x | { y | s} }, s is a set [x, y|l] = Cons(x, Cons(y, l)) r s = Union(r, s) r s = Intersection(r, s) x s = Member(x, s) r s = Subset(r, s)

The wumpus world Recall the wumpus agent receives l a percept vector [S, B, G, BUMP, S] As the percept is time critical, we add an integer as the time step l percept([S, B, G, None], 5) l S, B, G, etc. are constant symbols l The actions in wumpus world Turn(Right), Turn(Left), Forward, … l we want to pick up a best action for any time l

To choose a best action, we may ask a Best. Action(a, 5), for example l the result may be a = Grab (a Glitter!!) l But is it some straightforward? l we have to first tell KB what happens!! l s, b, u, c, t Percept([s, Breeze, g, m, c], t) Breeze(t) l s, b, u, c, t Percept([s, b, Glitter, m, c], t) Glitter(t) l and so on. l but it’s not enough l since we need to define additional rules l t Glitter(t) => Best. Action(Grab, t) l and so on. l

Defining environments Objects in the environment squares l pits l the wumpus l For any square, named as Square 1, 2 and so on. l for adjacent squares, we have to define them l l l pair by pair!! hence using a rule is much better

For the pits, we don’t need name them individually l we just need to use a unary predicate l l Pit(S), to indicate a square has a pit or not For the wumpus, there exists only one l it lives only in exactly one square l so, we may use Home(Wumpus) to name the square l l where Wumpus is a constant and Home a function

As the agent moves it changes over time l we use At(Agent, s, t) to specify l l at a time step, Agent is at s For the properties of the environment it is constant over time. l e. g. , a square is breezy (has a breeze) l s, t At(Agent, s, t) Breeze(t) => Breezy(s) The same for smelly (has a stench).

Diagnostic rules For a given percept, what does it mean? what results can be concluded? l e. g. , if a square is breezy, then what? l implies “some adjacent square has a pit!” s Breezy(s) => r Adjacent(r, s) Pit(r) l l For the reverse direction, is it true? yes, so we have s Breezy(s) <=> r Adjacent(r, s) Pit(r) l

Causal rules For a given result, what facts can be deduced? if r is a pit, then? l all adjacent squares of r are breezy l r Pit(r) => [ s Adjacent(r, s) Breezy(s)] l if all squares adjacent to a square s are not pits, then s is not breezy s [ r Adjacent(r, s) => Pit(r)] => Breezy(s) Basically, these rules are equivalent to previous bidirectional rule

Conclusion the facts or world description Whichever kind representation if the axioms correctly and completely describe the way the world works l and the way the percepts are produced l then any complete logical inference procedure successor function will infer the strongest possible description of the world state l given the available percepts l