Chapter 7 Exploring Measures of Variability Objectives Students

Chapter 7 Exploring Measures of Variability Objectives Students will be able to: 1) Calculate mean absolute deviation and standard deviation, and use these values to measure consistency 2) Test for a difference in standard deviations

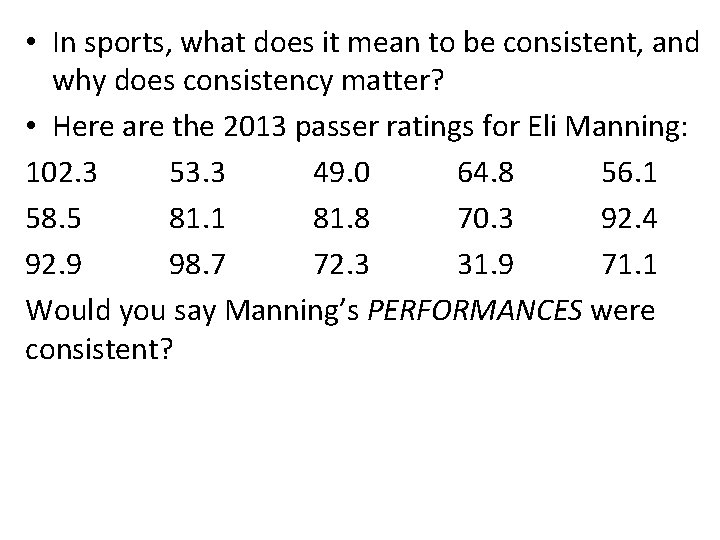
• In sports, what does it mean to be consistent, and why does consistency matter? • Here are the 2013 passer ratings for Eli Manning: 102. 3 53. 3 49. 0 64. 8 56. 1 58. 5 81. 1 81. 8 70. 3 92. 4 92. 9 98. 7 72. 3 31. 9 71. 1 Would you say Manning’s PERFORMANCES were consistent?

• To be consistent means that an athlete’s or team’s PERFORMANCES are very similar to each other. • Examples: – In basketball, a consistent player will score about the same number of points each game. – In swimming, a consistent swimmer will swim about the same time in each race. – In football, a consistent running back will gain about the same number of yards each game.

• Here are the distributions for two golfers. Both average 200 yards per drive. Which is more consistent? How can we measure the variability of each distribution? – Range -IQR • What are some problems with these measures? – The range is influenced by outliers. – IQR only measures the spread of the middle half of the observations, so it doesn’t tell us about the variability of the entire distribution.

• How can we measure variability using each value in a distribution? – Measure how far each value is from the center of the distribution, then find an average distance to the center. • This chapter we will focus on two measures of spread that use every PERFORMANCE in a distribution: the mean absolute deviation and the standard deviation. • These differ from range and IQR which only measure the distance between two positions in a distribution.

Mean Absolute Deviation (MAD) • How far is each of these points from the mean?

• A deviation measures the distance between an observed PERFORMANCE and the mean of its distribution: Deviation = PERFORMANCE – mean • The mean absolute deviation (MAD) measures the average distance the values in a distribution are from their mean.

• Former Chicago White Sox manager Ozzie Guillen once complained about his team’s lack of consistency. • From April 24 to May 4, 2010 (10 games), the White Sox opponents scored the following run totals: 4 2 4 6 5 6 6 12 1 7 • To get an overall measure of how variable these PERFORMANCES were from the mean, let’s calculate the MAD for this distribution.

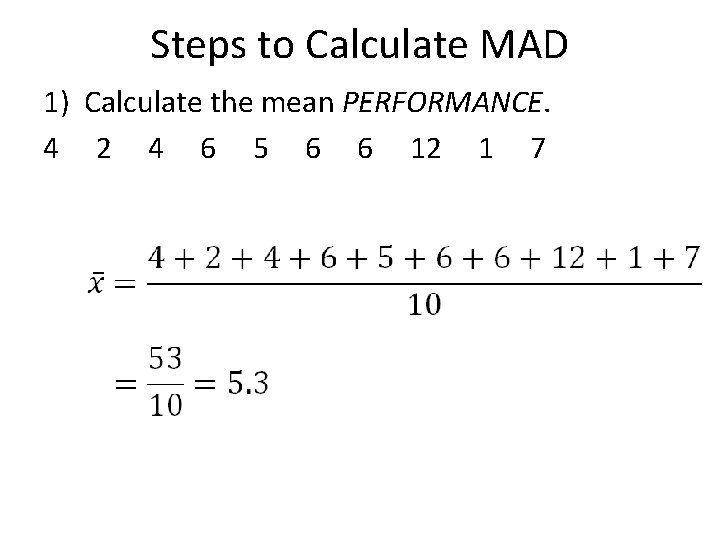
Steps to Calculate MAD 1) Calculate the mean PERFORMANCE. 4 2 4 6 5 6 6 12 1 7

2) Calculate the deviations from the mean PERFORMANCE. actual PERFORMANCE – mean PERFORMANCE • If a PERFORMANCE is above average, the deviation will be positive. • If a PERFORMANCE is below average, the deviation will be negative.

• The chart is also on pg 227.

3) Find the absolute value of each deviation. Why would we want to do this? If we were to simply add the deviations, the sum would be 0.

4) Calculate the mean of the absolute deviations. On average, the number of runs allowed by the White Sox was 2. 1 runs from their mean. Let’s compare this to the number of runs the White Sox scored themselves over these 10 games.

• Which distribution of PERFORMANCES looks more consistent? • It looks like the runs scored is more consistent. To confirm, let’s compare the MAD for each distribution.

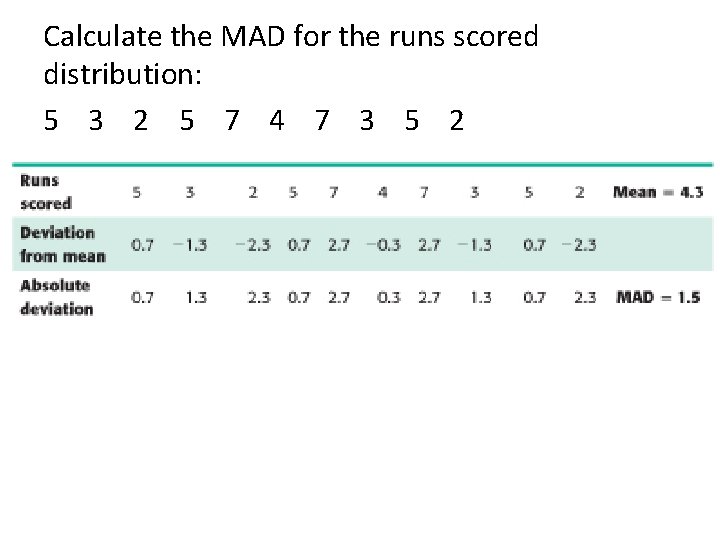
Calculate the MAD for the runs scored distribution: 5 3 2 5 7 4 7 3 5 2

• The MAD for the runs allowed distribution is 2. 1 runs and the MAD for the runs scored distribution is 1. 5 runs. Is our hunch confirmed? • The runs scored distribution is more consistent. • The smaller the MAD, the more consistent the PERFORMANCES are.

The Standard Deviation • When calculating mean absolute deviation, we had to use absolute value to assure that each deviation would be positive. • Can anyone think of another way we could have made each deviation positive? – Squaring each deviation

• Standard deviation measures the variability in a distribution using the squared deviations from the mean. • You may be asking yourself “What are the benefits to using standard deviation over MAD? ” – 1) We will be working a lot with the Normal distribution (spoiler alert: next chapter!) and the Normal distribution is defined in terms of the standard deviation – 2) Many important techniques in statistics are based on the idea of squared deviations, such as least-squares regression lines (Chapter 11)

What does standard deviation measure? • Standard deviation measures the typical distance between an athlete’s PERFORMANCES and his or her ABILITY. In other terms, it is the typical distance between observations and the mean. • To better understand this, let’s look at an example…

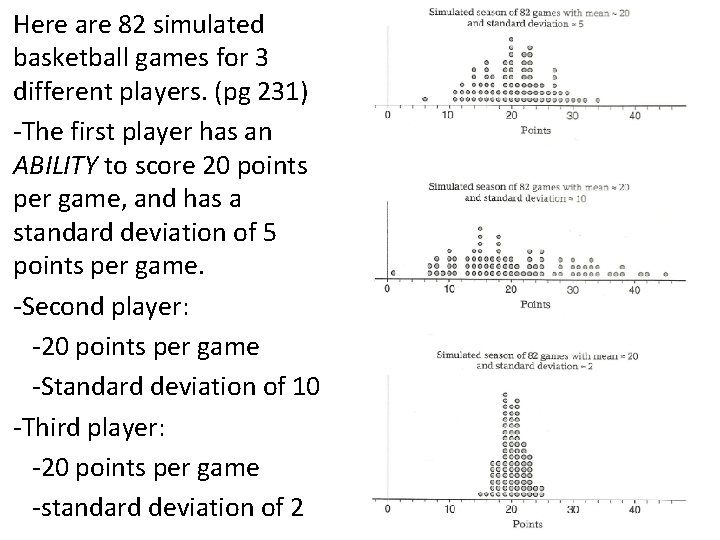
Here are 82 simulated basketball games for 3 different players. (pg 231) -The first player has an ABILITY to score 20 points per game, and has a standard deviation of 5 points per game. -Second player: -20 points per game -Standard deviation of 10 -Third player: -20 points per game -standard deviation of 2

• The first player’s average is 20 points per game. However, the individual game PERFORMANCES varied somewhat, due to RANDOM CHANCE. • The standard deviation is 5, meaning typically his PERFORMANCES were about 5 points from his ABILITY.

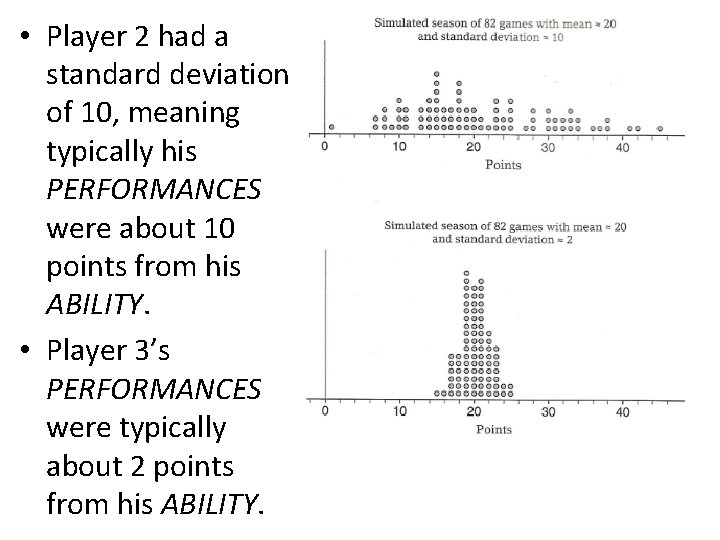
• Player 2 had a standard deviation of 10, meaning typically his PERFORMANCES were about 10 points from his ABILITY. • Player 3’s PERFORMANCES were typically about 2 points from his ABILITY.

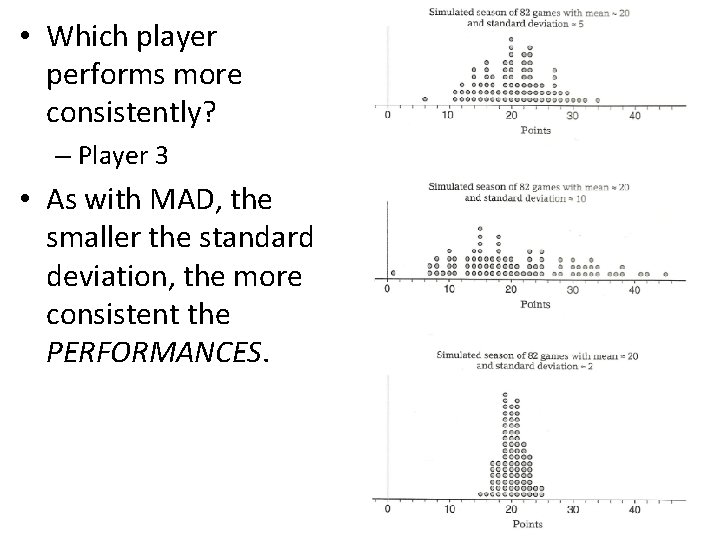
• Which player performs more consistently? – Player 3 • As with MAD, the smaller the standard deviation, the more consistent the PERFORMANCES.

Calculating the Standard Deviation • One thing to keep in mind is that standard deviation will be a little larger than the mean absolute deviation. Why might this be? • Instead of taking absolute value of the deviations, we are squaring them. This will give extra weight to values far from the mean.

• Let’s look at the steps to calculate standard deviation. • We will use our previous runs allowed data from the White Sox example. 4 2 4 6 5 6 6 12 1 7 • The first two steps are exactly the same as the first to steps to calculating the MAD.

• Step 1: Calculate the mean.

• Step 2: Find the deviations from the mean. (pg 234)

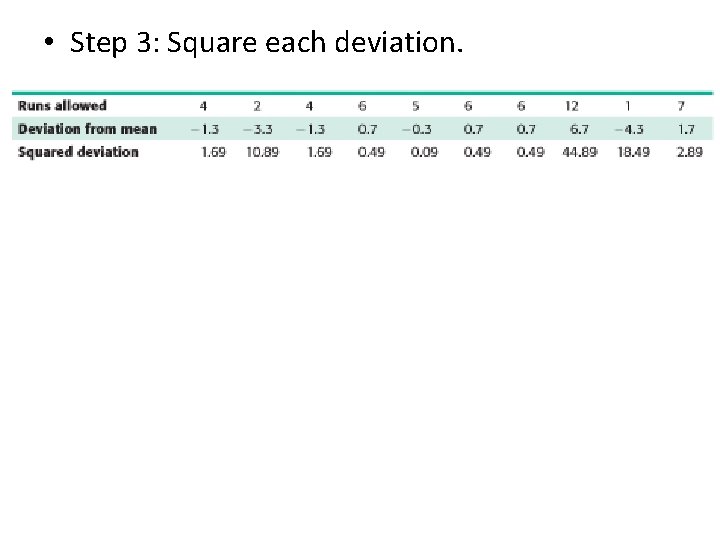
• Step 3: Square each deviation.

• Step 4: a) Add the squared deviations b) Divide this total by 1 less than the total number of observations (n-1) c) Take the square root.

Using Technology to Calculate the Standard Deviation Notation • The standard deviation of a set of PERFORMANCES is denoted by a lowercase “s. ” • On the TI-84, we can find the standard deviation the same way we previously found summary statistics.

Steps to Calculate Standard Deviation on the TI-84 Let’s use the same 10 White Sox observations: 4 2 4 6 5 6 6 12 1 7 1) Enter the observations into a list. 2) Press STAT, go to the CALC column, choose 1 -Var Stats, and select your list. 3) The standard deviation is labeled sx. The value should be 3. 02 to match our previous calculation.

Testing for a Difference in Standard Deviations • Previously, we compared an athlete’s PERFORMANCES in two different contexts to investigate if the athlete had a greater ABILITY in one of those contexts. • Since we never truly know an athlete’s ABILITY, we had to estimate it with PERFORMANCES, which are partly due to RANDOM CHANCE.

• The same concept is applicable to standard deviation. • An athlete’s true standard deviation would be their standard deviation after an infinite number of PERFORMANCES. • Observed standard deviation is standard deviation based on observed PERFORMANCES. • Observed standard deviation is used to estimate true standard deviation. Keep in mind observed standard deviation will vary from true standard deviation due to RANDOM CHANCE.

Let’s talk about golf!!!

Experiment: Which 7 -iron is more consistent? • Consistency is very important in golf. • Knowing exactly how far shots will travel with each different golf club is a huge strategic advantage. • Let’s analyze an experiment to determine if a golfer is more consistent with a new 7 -iron.

• Jimmy is considering buying a new 7 -iron, hoping it will make his shots more consistent. • To investigate, he decided to conduct an experiment. • Luckily for Jimmy, he has a twin brother Sean that happens to have the new 7 -iron that Jimmy wants to buy. • Jimmy will use his current 7 -iron and borrow his brother’s 7 -iron to see which of the two clubs makes the distance he hits a 7 -iron less variable.

• What will be the explanatory and response variables for this experiment? Explanatory: the club (current or new) Response: distance the ball travels • What are some variables we would want to control? Same shoes, same type of golf ball, same gloves, same location, same time, etc…

• Jimmy will hit 20 golf balls in total. How can randomization be incorporated into the experiment? Randomize the order in which the clubs are used. Take 20 note cards, write a “C” on 10 for the current club and a “N” on 10 for the new club. Shuffle the cards, take one at a time and use that club.

• Is it possible for Jimmy to be blind? No. He needs to know what club to use, and it would be rather difficult to disguise the clubs. • Now let’s look at the results…

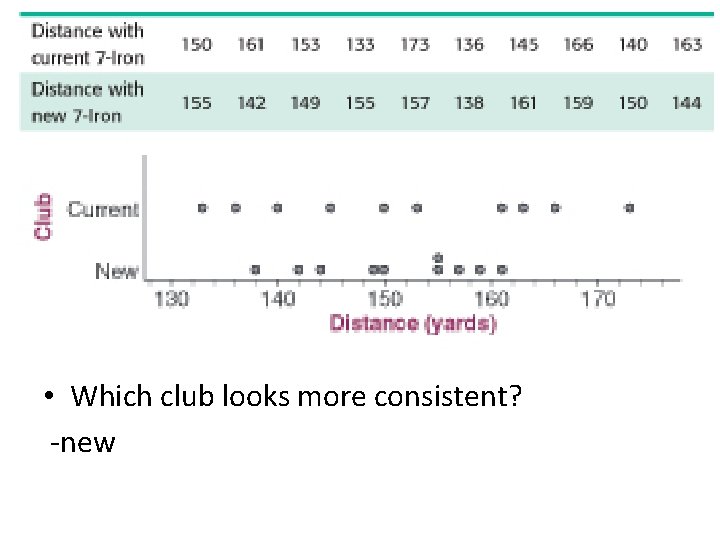
• Which club looks more consistent? -new

• Let’s perform a hypothesis test using the difference in observed standard deviations (current – new) as the test statistic. • What are the hypotheses we are interested in testing?

• The standard deviation for the current 7 -iron is 13. 56 yards and the standard deviation of the new 7 -iron is 7. 72 yards. • What is the value of the test statistic? (current – new)= 13. 56 -7. 72 = 5. 84 yards

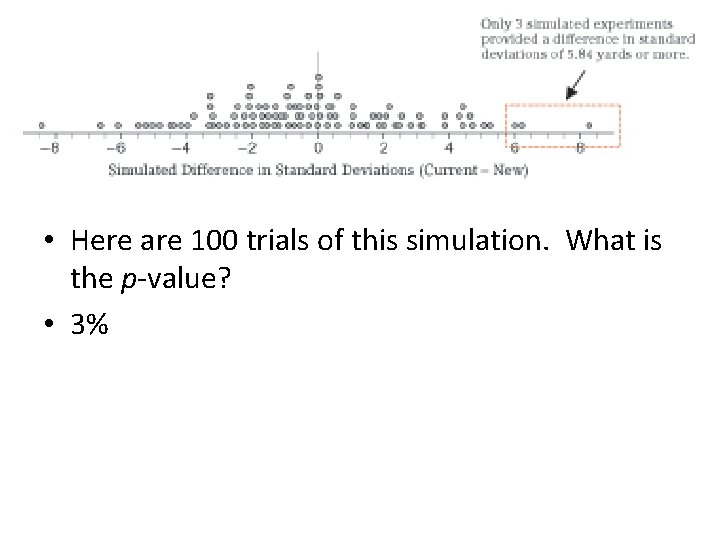
• Here are 100 trials of this simulation. What is the p-value? • 3%

• With a p-value of 3%, what would be the conclusion? • Because the p-value of 3% is lower than the significance level of 5%, we reject the null hypothesis. There is convincing evidence to support the claim that Jimmy’s true standard deviation is smaller with the new club. • Therefore, he will be more consistent if he uses the new club.