Chapter 7 Counters and Registers 7 th April

Chapter 7 Counters and Registers 7 th April 2009

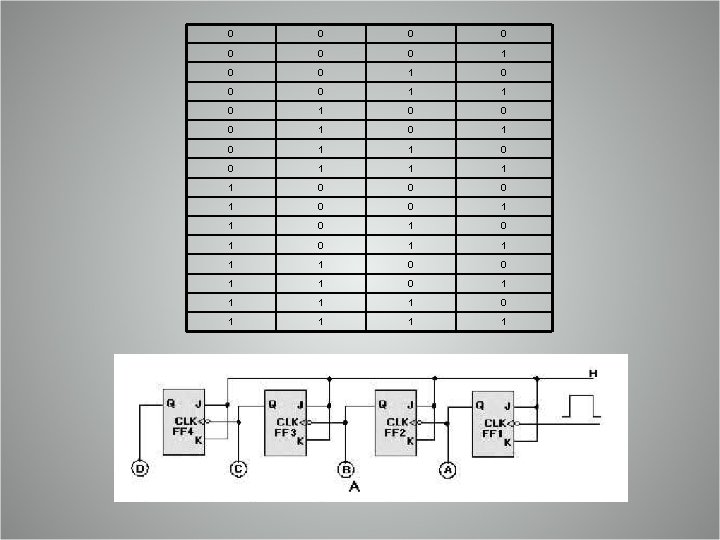
Introduction § Circuits for counting are needed in computer and digital systems § A Counter circuit consists of a series of flipflops (FFs) connected together to produce a sequence of states § The state is often referred as a “modulo” § For example: § Counter that counts from 0000 to 1111 is called modulo-16 counter, because it has 16 states.

Types of Counters § Counters can be classifed into two categories: § Asynchronous (Ripple) Counters § The first FF is connected to external clock pulse and then each successive FF clock (CLK) is connected to the output (Q) of the previous FF § Synchronous Counters § Every FF is connected to an external clock pulse

7 -1 Asynchronous (Ripple) Counters § A counter can count up or down by ones, twos or as desired. § A four-stage counter will have 16 stable states § RECALL : 24 = 16 § Therefore, Four-stage counter can be called as MODOULU-16 Counter

7 -1 Asynchronous (Ripple) Counters § Asynchronous counter have the first flipflop connected to an external clock and the rest of the flip-flop clocks are connected to the output of the previous flip-flop

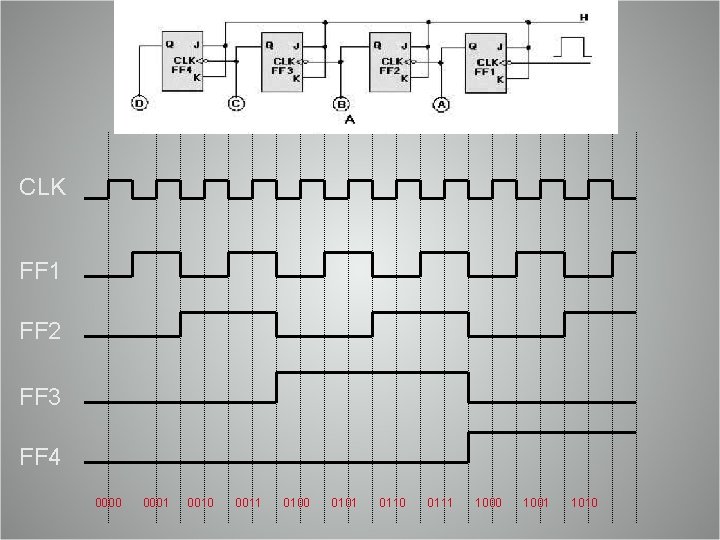
0 0 0 0 1 1 0 0 0 1 0 1 1 0 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 0 1 1

CLK FF 1 FF 2 FF 3 FF 4 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010

Frequency Division § In any counter the signal at the output of the last flip-flop will have a frequency equal to the input clock frequency divided by the MOD number of the counter. § E. g. § For a MOD-16 counter, the output from the last FF will have a frequency of 1/16 of the input clock frequency.

Frequency Division § For the first flip-flop the frequency will be 1/2 of the original CLK frequency. While for the second flipflop the frequency will be 1/4 of the original CLK frequency. § GOLDEN RULE: for each flip-flop. Divide by 2 !

Question! § How many flip-flops are required for a MOD-32 counter? § 25 = 32, therefore 5 Flip-Flops are required § Now! § How many flip-flops are required for a MOD-60 counter? § 26 =64 >60 !!!!! § In the next lecture, we will find a solution to obtain 60 counts only.

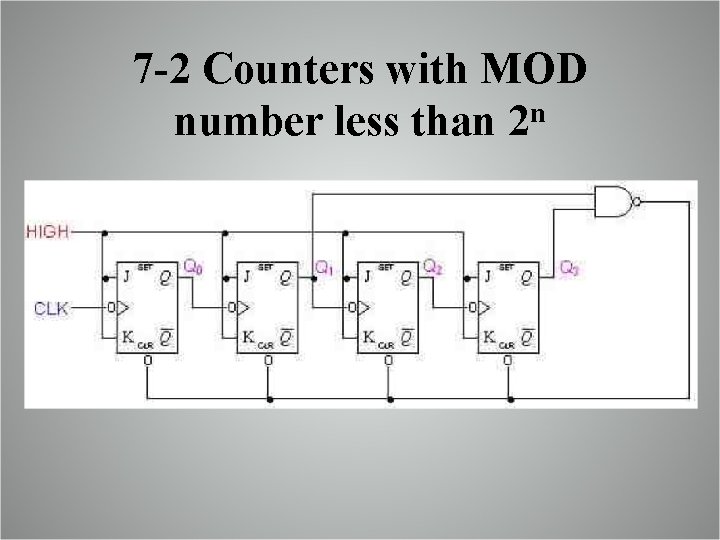
7 -2 Counters with MOD number less than 2 n § In the previous lecture, we’ve learned about counters that are limited to MOD numbers equal to 2 N, where N is the number of Flip-Flops. § The basic counter can be modified to produce MOD number that is less than 2 N by allowing the counter to skip some states. § This can be achieved by forcing the counter to recycle the count before going through all the states.

7 -2 Counters with MOD number less than 2 n § A Famous counter of this type is the decade counter MOD-10. That counts from 0000 (0) to 1010 (10). It is often called BCD counter because it uses only the 10 BCD group Clock Q 3 Q 2 Q 1 Q 0 0 0 1 2 0 0 1 0 3 0 0 1 1 4 0 1 0 0 5 0 1 6 0 1 1 0 7 0 1 1 1 8 1 0 0 0 9 1 0 0 1

7 -2 Counters with MOD number less than 2 n

Changing the MOD number § To design a counter of MOD-X: 1. Find the smallest number of FFs such that 2 N ≥ X, and connect them as a counter. If 2 N = X then skip the next steps. 2. Connect a NAND gate to the asynchronous CLEAR inputs of all the FFs. 3. Determine which FFs will be in the HIGH state at a count = X; then connect the normal outputs of these FFs to the NAND gate inputs.

Example 1 § What is the MOD number of the following Counter ? And what is the frequency at D ? MOD-14, (1110). At D, the frequency would be 30 k. Hz / 14 = 2. 14 k. Hz

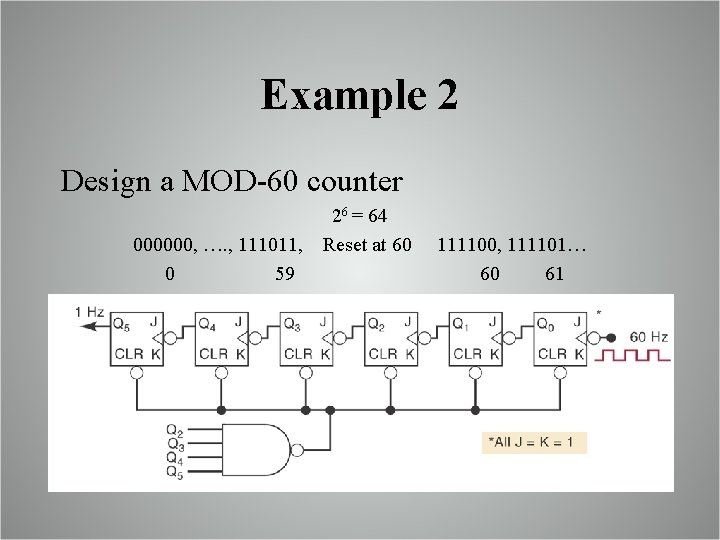
Example 2 Design a MOD-60 counter 000000, …. , 111011, 0 59 26 = 64 Reset at 60 111100, 111101… 60 61

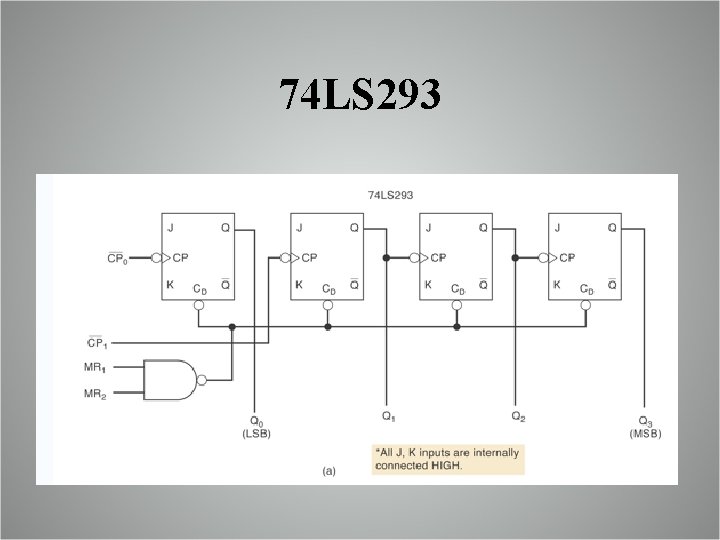
7 -3 IC ASYNCHRONOUS COUNTERS § There are several TTL and CMOS asynchronous counter ICs. One of them is the TTL 74 LS 293

7 -3 IC ASYNCHRONOUS COUNTERS § It has four J-K flip-flops, with outputs Q 3 Q 2 Q 1 Q 0 § Each FF has a CP (clock pulse) input, just another name for CLK. The clock inputs to Q 1 and Q 0, labeled (CP 0)’ and (CP 1)’ are externally accessible (pin 11 and 10, respectively). § Each FF has an asynchronous CLEAR input CD. These are § Flip flops Q 3 Q 2 Q 1 are connected as a 3 -bit ripple counter. § Flip flop Q 0 is not connected to anything internally. This allows the user the option of either connecting Q 0 to Q 1 to form a 4 -bit counter or using Q 0 separately if desired.

74 LS 293

Example 3 § Show the 74 LS 293 should be connected to operate as a MOD-16 counter with a 10 -k. Hz clock input. Determine the frequency at Q 3. § MOD-16 needs 4 FFs. Therefore, The output of Q 0 must be connected to the next FF. Assume a clock frequency of 10 k. Hz, therefore Frequency at Q 3 would equal 10 k. Hz/16 = 625 k. Hz

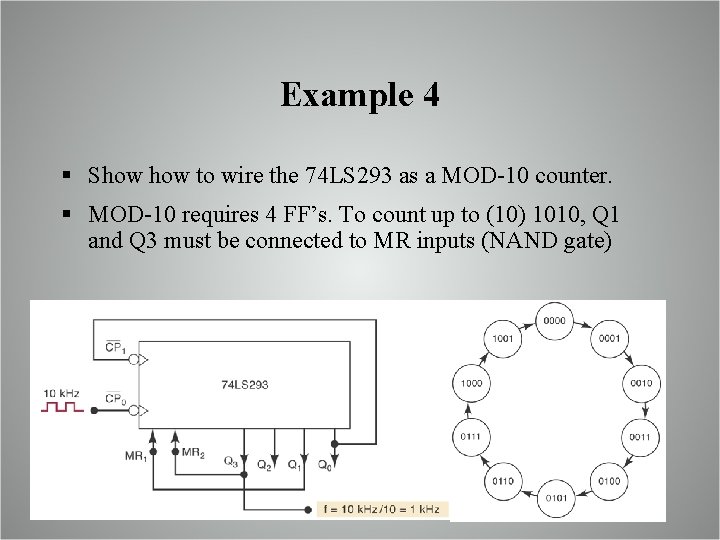
Example 4 § Show to wire the 74 LS 293 as a MOD-10 counter. § MOD-10 requires 4 FF’s. To count up to (10) 1010, Q 1 and Q 3 must be connected to MR inputs (NAND gate)

Example 5 § Show to wire the 74 LS 293 as a MOD-14 counter. § When the counter reaches (14) 1110 it should reset. That is when Q 1=Q 2=Q 3=1. But the built-in NAND gate has only 2 inputs. Therefore, an extra AND gate must be added to have all the three inputs fed together.