Chapter 7 Arrays Arrays Arrays are objects that

Chapter 7 Arrays

Arrays • Arrays are objects that help us organize large amounts of information • Chapter 7 focuses on: § § § array declaration and use bounds checking and capacity arrays that store object references multidimensional arrays variable length parameter lists © 2004 Pearson Addison-Wesley. All rights reserved 2

Outline Declaring and Using Arrays of Objects Two-Dimensional Arrays Variable Length Parameter Lists © 2004 Pearson Addison-Wesley. All rights reserved 3
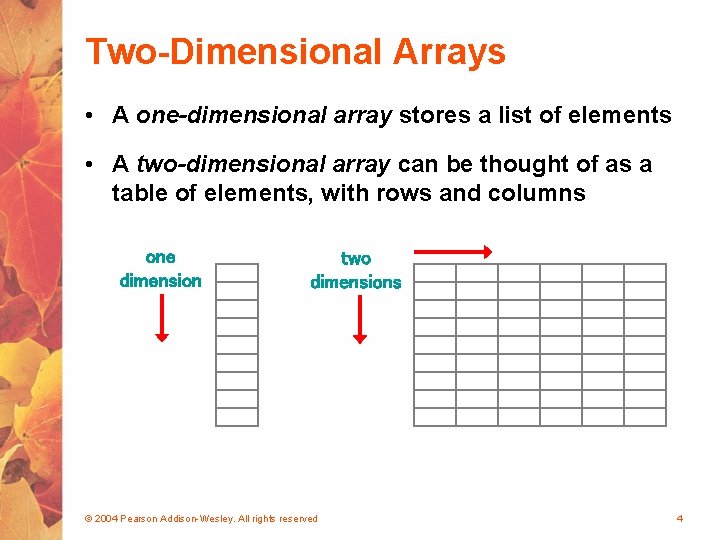
Two-Dimensional Arrays • A one-dimensional array stores a list of elements • A two-dimensional array can be thought of as a table of elements, with rows and columns one dimension two dimensions © 2004 Pearson Addison-Wesley. All rights reserved 4

Two-Dimensional Arrays • To be precise, in Java a two-dimensional array is an array of arrays • A two-dimensional array is declared by specifying the size of each dimension separately: int[][] scores = new int[12][50]; • A array element is referenced using two index values: value = scores[3][6] • The array stored in one row can be specified using one index © 2004 Pearson Addison-Wesley. All rights reserved 5
![2 D Array in Memory [0] 692134 [0] [1] [0] 187328 [1] [2] [3] 2 D Array in Memory [0] 692134 [0] [1] [0] 187328 [1] [2] [3]](http://slidetodoc.com/presentation_image_h/d4d0155b5ba8048b5305fe8c59fda753/image-6.jpg)
2 D Array in Memory [0] 692134 [0] [1] [0] 187328 [1] [2] [3] 655615 621077 492428 [1] 118572 [2] [3] 61911 36152 … [pop. length-1] © 2004 Pearson Addison-Wesley. All rights reserved 6
![Two-Dimensional Arrays Expression table Type int[][] Description table[5] int[] array of integers table[5][12] integer Two-Dimensional Arrays Expression table Type int[][] Description table[5] int[] array of integers table[5][12] integer](http://slidetodoc.com/presentation_image_h/d4d0155b5ba8048b5305fe8c59fda753/image-7.jpg)
Two-Dimensional Arrays Expression table Type int[][] Description table[5] int[] array of integers table[5][12] integer 2 D array of integers, or array of integer arrays int[][] table = new int[5][10]; // Load the table with values for (int row=0; row < table. length; row++) for (int col=0; col < table[row]. length; col++) table[row][col] = row * 10 + col; // Print the table for (int row=0; row < table. length; row++) { for (int col=0; col < table[row]. length; col++) System. out. print (table[row][col] + "t"); System. out. println(); } • From Two. DArray. java (page 399) © 2004 Pearson Addison-Wesley. All rights reserved 7

Soda. Survey. java //-----------------------------// Determines and prints the average of each row (soda) and // each column (respondent) of the survey scores. //-----------------------------public static void main (String[] args) { int[][] scores = { {3, 4, 5, 2, 1, 4, 3, 2, 4, 4}, {2, 4, 3, 3, 2, 1, 2, 2}, {3, 5, 4, 5, 5, 3, 2, 5, 5, 5}, {1, 1, 1, 3, 1, 2, 1, 3, 2, 4} }; final int SODAS = scores. length; final int PEOPLE = scores[0]. length; int[] soda. Sum = new int[SODAS]; int[] person. Sum = new int[PEOPLE]; for (int soda=0; soda < SODAS; soda++) for (int person=0; person < PEOPLE; person++) { soda. Sum[soda] += scores[soda][person]; person. Sum[person] += scores[soda][person]; } © 2004 Pearson Addison-Wesley. All rights reserved 8

Soda. Survey. java Decimal. Format fmt = new Decimal. Format ("0. #"); System. out. println ("Averages: n"); for (int soda=0; soda < SODAS; soda++) System. out. println ("Soda #" + (soda+1) + ": " + fmt. format ((float)soda. Sum[soda]/PEOPLE)); System. out. println (); for (int person =0; person < PEOPLE; person++) System. out. println ("Person #" + (person+1) + ": " + fmt. format ((float)person. Sum[person]/SODAS)); } } © 2004 Pearson Addison-Wesley. All rights reserved 9

Multidimensional Arrays • An array can have many dimensions – if it has more than one dimension, it is called a multidimensional array • Each dimension subdivides the previous one into the specified number of elements • Each dimension has its own length constant • Because each dimension is an array of array references, the arrays within one dimension can be of different lengths § these are sometimes called ragged arrays © 2004 Pearson Addison-Wesley. All rights reserved 10

Exercise 1 • Write a code fragment that calculates the product of all the entries on the main diagonal of a square array of doubles called numbers. © 2004 Pearson Addison-Wesley. All rights reserved 11

Exercise 2 • Write a code fragment that calculates the product of all the entries on the skew diagonal of a square array of doubles called numbers (the skew diagonal is the one from the lower left corner to the upper right corner). (0, 3) (1, 2) (2, 1) (3, 0) © 2004 Pearson Addison-Wesley. All rights reserved 12
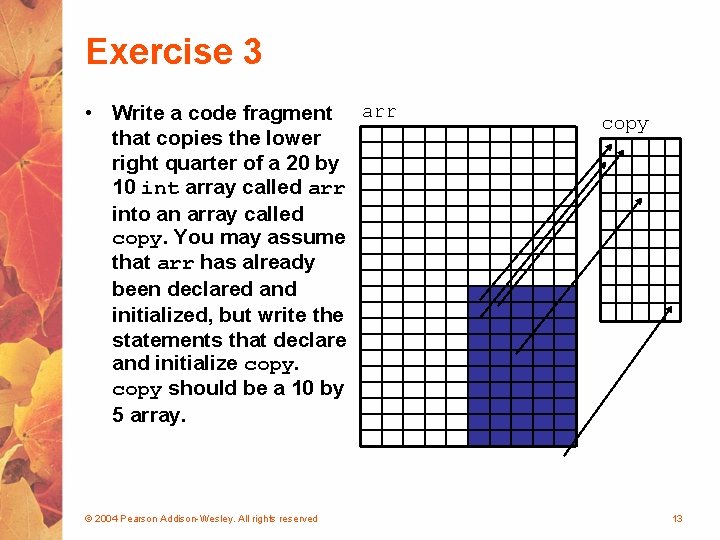
Exercise 3 • Write a code fragment arr that copies the lower right quarter of a 20 by 10 int array called arr into an array called copy. You may assume that arr has already been declared and initialized, but write the statements that declare and initialize copy should be a 10 by 5 array. © 2004 Pearson Addison-Wesley. All rights reserved copy 13
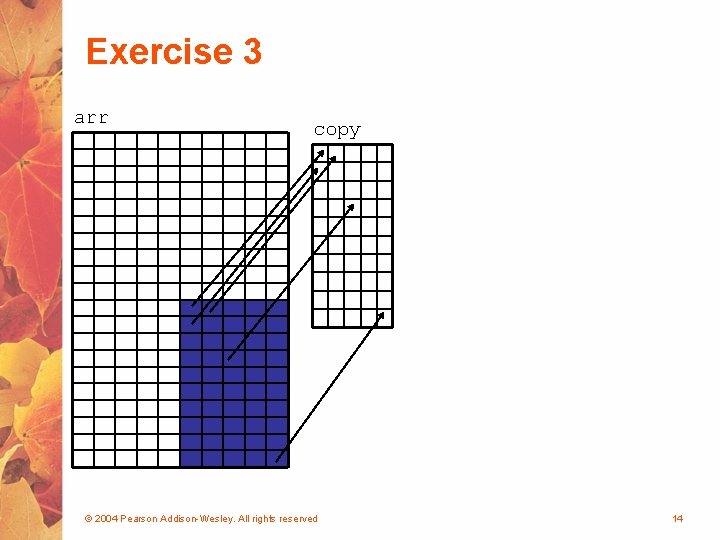
Exercise 3 arr copy © 2004 Pearson Addison-Wesley. All rights reserved 14

Outline Declaring and Using Arrays of Objects Two-Dimensional Arrays Variable Length Parameter Lists © 2004 Pearson Addison-Wesley. All rights reserved 15

Variable Length Parameter Lists • Suppose we wanted to create a method that processed a different amount of data from one invocation to the next • For example, let's define a method called average that returns the average of a set of integer parameters // one call to average three values mean 1 = average (42, 69, 37); // another call to average seven values mean 2 = average (35, 43, 93, 23, 40, 21, 75); © 2004 Pearson Addison-Wesley. All rights reserved 16

Variable Length Parameter Lists • We could define overloaded versions of the average method § Downside: we'd need a separate version of the method for each parameter count • We could define the method to accept an array of integers § Downside: we'd have to create the array and store the integers prior to calling the method each time • Instead, Java provides a convenient way to create variable length parameter lists © 2004 Pearson Addison-Wesley. All rights reserved 17

Variable Length Parameter Lists • Using special syntax in the formal parameter list, we can define a method to accept any number of parameters of the same type • For each call, the parameters are automatically put into an array for easy processing in the method Indicates a variable length parameter list public double average (int. . . list) { // whatever } element array type name © 2004 Pearson Addison-Wesley. All rights reserved 18

Summary • Chapter 7 has focused on: § § § array declaration and use bounds checking and capacity arrays that store object references variable length parameter lists multidimensional arrays © 2004 Pearson Addison-Wesley. All rights reserved 19

Chapter 11 Recursion

Recursion • Recursion is a fundamental programming technique that can provide an elegant solution certain kinds of problems • Chapter 11 focuses on: § § thinking in a recursive manner programming in a recursive manner the correct use of recursion examples © 2004 Pearson Addison-Wesley. All rights reserved 21

Outline Recursive Thinking Recursive Programming Using Recursion © 2004 Pearson Addison-Wesley. All rights reserved 22

Recursive Thinking • A recursive definition is one which uses the word or concept being defined in the definition itself • When defining an English word, a recursive definition is often not helpful • But in other situations, a recursive definition can be an appropriate way to express a concept • Before applying recursion to programming, it is best to practice thinking recursively © 2004 Pearson Addison-Wesley. All rights reserved 23

Recursive Definitions • Consider the following list of numbers: 24, 88, 40, 37 • Such a list can be defined as follows: A LIST is a: or a: number comma LIST • That is, a LIST is defined to be a single number, or a number followed by a comma followed by a LIST • The concept of a LIST is used to define itself © 2004 Pearson Addison-Wesley. All rights reserved 24

Recursive Definitions • The recursive part of the LIST definition is used several times, terminating with the non-recursive part: number comma LIST 24 , 88, 40, 37 number comma LIST 88 , 40, 37 number comma LIST 40 , 37 number 37 © 2004 Pearson Addison-Wesley. All rights reserved 25

Infinite Recursion • All recursive definitions have to have a nonrecursive part • If they didn't, there would be no way to terminate the recursive path • Such a definition would cause infinite recursion • This problem is similar to an infinite loop, but the non-terminating "loop" is part of the definition itself • The non-recursive part is often called the base case © 2004 Pearson Addison-Wesley. All rights reserved 26

Recursive Definitions • N!, for any positive integer N, is defined to be the product of all integers between 1 and N inclusive • This definition can be expressed recursively as: 1! N! = = 1 N * (N-1)! • A factorial is defined in terms of another factorial • Eventually, the base case of 1! is reached © 2004 Pearson Addison-Wesley. All rights reserved 27

Recursive Definitions 5! 120 5 * 4! 24 4 * 3! 6 3 * 2! 2 * 1! 2 1 © 2004 Pearson Addison-Wesley. All rights reserved 28

Outline Recursive Thinking Recursive Programming Using Recursion © 2004 Pearson Addison-Wesley. All rights reserved 29

Recursive Programming • A method in Java can invoke itself; if set up that way, it is called a recursive method • The code of a recursive method must be structured to handle both the base case and the recursive case • Each call to the method sets up a new execution environment, with new parameters and local variables • As with any method call, when the method completes, control returns to the method that invoked it (which may be an earlier invocation of itself) © 2004 Pearson Addison-Wesley. All rights reserved 30

Recursive Programming • Consider the problem of computing the sum of all the numbers between 1 and any positive integer N • This problem can be recursively defined as: © 2004 Pearson Addison-Wesley. All rights reserved 31

Recursive Programming // This method returns the sum of 1 to num public int sum (int num) { int result; if (num == 1) result = 1; else result = num + sum (n-1); return result; } © 2004 Pearson Addison-Wesley. All rights reserved 32
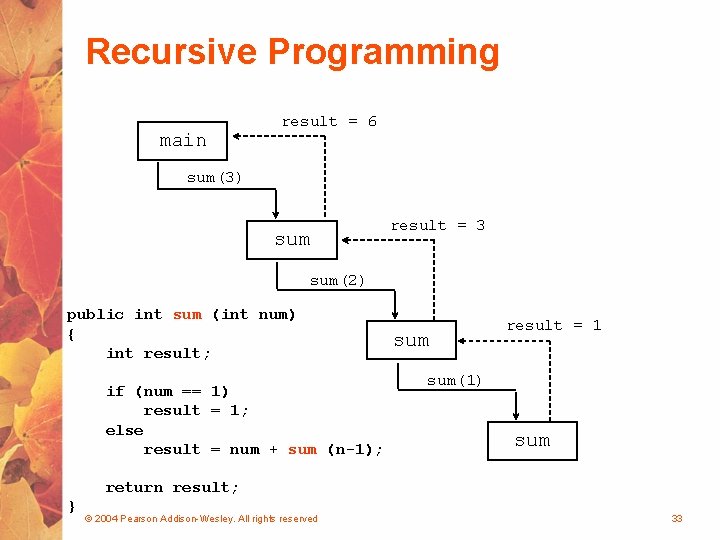
Recursive Programming main result = 6 sum(3) sum result = 3 sum(2) public int sum (int num) { int result; if (num == 1) result = 1; else result = num + sum (n-1); sum result = 1 sum(1) sum return result; } © 2004 Pearson Addison-Wesley. All rights reserved 33

Recursive Programming • Note that just because we can use recursion to solve a problem, doesn't mean we should • For instance, we usually would not use recursion to solve the sum of 1 to N problem, because the iterative version is easier to understand • However, for some problems, recursion provides an elegant solution, often cleaner than an iterative version • You must carefully decide whether recursion is the correct technique for any problem © 2004 Pearson Addison-Wesley. All rights reserved 34

Indirect Recursion • A method invoking itself is considered to be direct recursion • A method could invoke another method, which invokes another, etc. , until eventually the original method is invoked again • For example, method m 1 could invoke m 2, which invokes m 3, which in turn invokes m 1 again • This is called indirect recursion, and requires all the same care as direct recursion • It is often more difficult to trace and debug © 2004 Pearson Addison-Wesley. All rights reserved 35
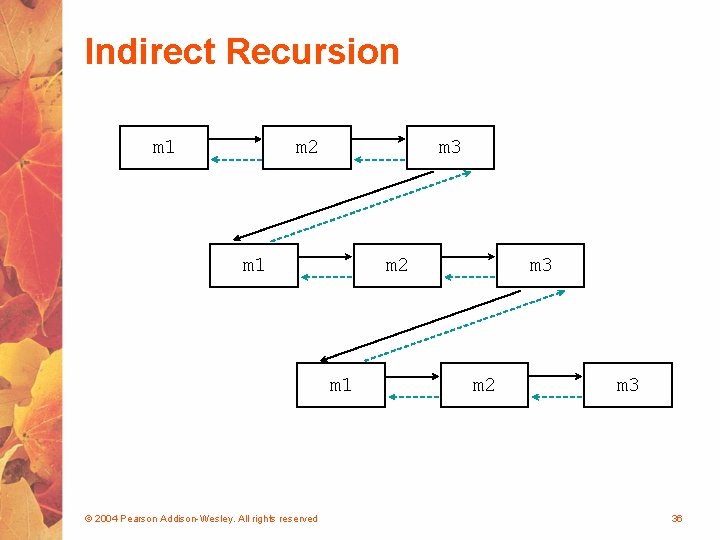
Indirect Recursion m 1 m 2 m 3 m 1 m 2 m 1 © 2004 Pearson Addison-Wesley. All rights reserved m 3 m 2 m 3 36

Outline Recursive Thinking Recursive Programming Using Recursion © 2004 Pearson Addison-Wesley. All rights reserved 37

Maze Traversal • We can use recursion to find a path through a maze • From each location, we can search in each direction • Recursion keeps track of the path through the maze • The base case is an invalid move or reaching the final destination • See Maze. Search. java (page 583) • See Maze. java (page 584) © 2004 Pearson Addison-Wesley. All rights reserved 38

Maze. java //******************************* // Maze. java Author: Lewis/Loftus // // Represents a maze of characters. The goal is to get from // the top left corner to the bottom right, following a path // of 1 s. //******************************* public class Maze { private final int TRIED = 3; private final int PATH = 7; private int[][] grid = { {1, 1, 1, 0, 0, 0, 1, 1}, {1, 0, 1, 1, 0, 0, 1}, {0, 0, 1, 0, 0}, {1, 1, 1, 0, 1, 1, 1}, {1, 0, 0, 1, 1, 1, 0, 0, 1}, {1, 0, 1, 1, 1, 0, 1, 1}, {1, 0, 0, 0, 0}, {1, 1, 1, 1} }; © 2004 Pearson Addison-Wesley. All rights reserved 39

Maze. java //-----------------------------// Attempts to recursively traverse the maze. Inserts // special characters indicating locations that have been // tried and that eventually become part of the solution. //-----------------------------public boolean traverse (int row, int column) { boolean done = false; if (valid (row, column)) { grid[row][column] = TRIED; // this cell has been tried if (row == grid. length-1 && column == grid[0]. length-1) done = true; // the maze is solved else { © 2004 Pearson Addison-Wesley. All rights reserved 40

Maze. java done = traverse (row+1, column); if (!done) done = traverse (row, column+1); if (!done) done = traverse (row-1, column); if (!done) done = traverse (row, column-1); // down // right // up // left } if (done) // this location is part of the final path grid[row][column] = PATH; } return done; } © 2004 Pearson Addison-Wesley. All rights reserved 41

Maze. java //------------------------------// Determines if a specific location is valid. //------------------------------private boolean valid (int row, int column) { boolean result = false; // check if cell is in the bounds of the matrix if (row >= 0 && row < grid. length && column >= 0 && column < grid[row]. length) // check if cell is not blocked and not previously // tried if (grid[row][column] == 1) result = true; return result; } © 2004 Pearson Addison-Wesley. All rights reserved 42

Maze. java //------------------------------// Returns the maze as a string. //------------------------------public String to. String () { String result = "n"; for (int row=0; row < grid. length; row++) { for (int column=0; column < grid[row]. length; column++) result += grid[row][column] + ""; result += "n"; } return result; } } © 2004 Pearson Addison-Wesley. All rights reserved 43

Maze. Search. java public class Maze. Search { //-----------------------------// Creates a new maze, prints its original form, attempts // to solve it, and prints out its final form. //-----------------------------public static void main (String[] args) { Maze labyrinth = new Maze(); System. out. println (labyrinth); if (labyrinth. traverse (0, 0)) System. out. println ("The maze was successfully traversed!"); else System. out. println ("There is no possible path. "); System. out. println (labyrinth); } } © 2004 Pearson Addison-Wesley. All rights reserved 44
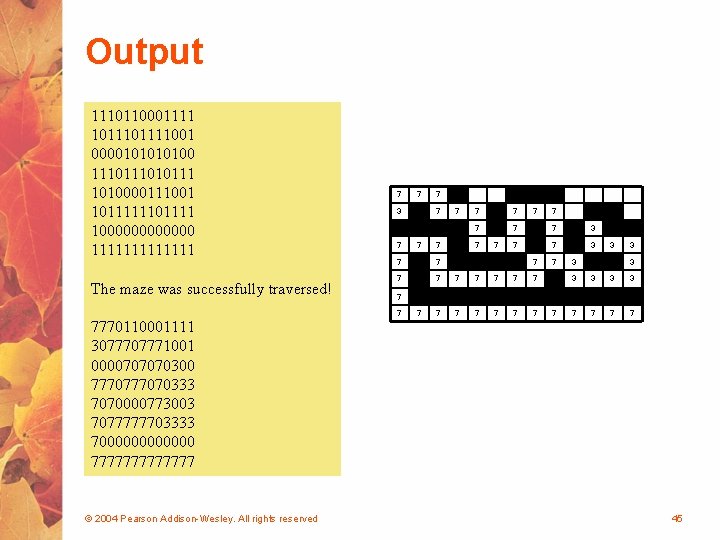
Output 1110110001111 101111001 000010100 111010111 1010000111001 1011111101111 1000000 1111111 The maze was successfully traversed! 7770110001111 307771001 0000707070300 777070333 7070000773003 7077777703333 7000000 7777777 © 2004 Pearson Addison-Wesley. All rights reserved 7 7 3 7 7 7 7 7 7 7 7 3 3 3 3 7 7 7 7 45

Towers of Hanoi • The Towers of Hanoi is a puzzle made up of three vertical pegs and several disks that slide on the pegs • The disks are of varying size, initially placed on one peg with the largest disk on the bottom with increasingly smaller ones on top • The goal is to move all of the disks from one peg to another under the following rules: § We can move only one disk at a time § We cannot move a larger disk on top of a smaller one © 2004 Pearson Addison-Wesley. All rights reserved 46
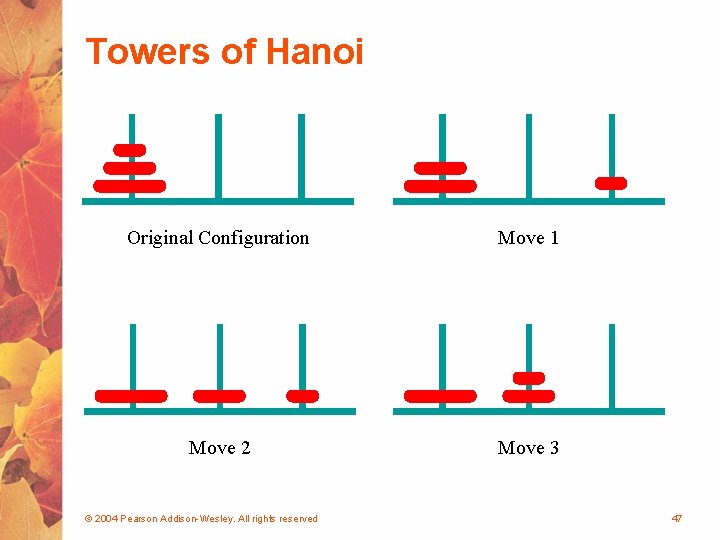
Towers of Hanoi Original Configuration Move 1 Move 2 Move 3 © 2004 Pearson Addison-Wesley. All rights reserved 47
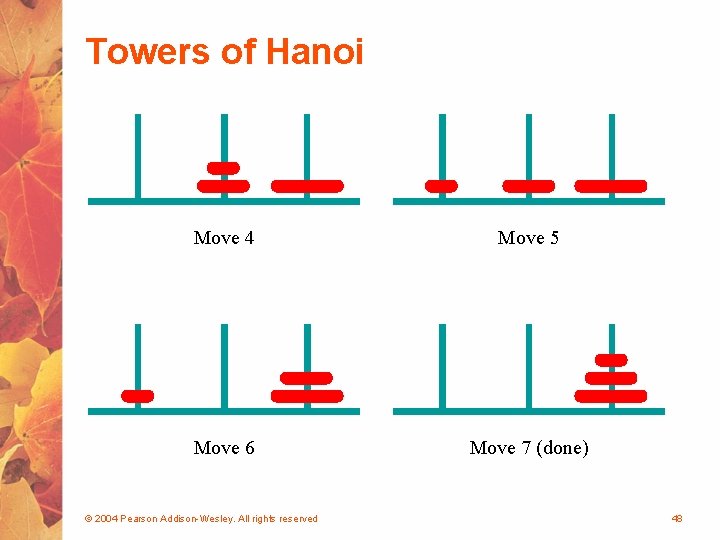
Towers of Hanoi Move 4 Move 5 Move 6 Move 7 (done) © 2004 Pearson Addison-Wesley. All rights reserved 48

Towers of Hanoi • An iterative solution to the Towers of Hanoi is quite complex • A recursive solution is much shorter and more elegant • See Solve. Towers. java (page 590) • See Towers. Of. Hanoi. java (page 591) © 2004 Pearson Addison-Wesley. All rights reserved 49

Towers. Of. Hanoi. java public class Towers. Of. Hanoi { private int total. Disks; //-----------------------------// Sets up the puzzle with the specified number of disks. //-----------------------------public Towers. Of. Hanoi (int disks) { total. Disks = disks; } //-----------------------------// Performs the initial call to move. Tower to solve the // puzzle. Moves the disks from tower 1 to tower 3 using // tower 2. //-----------------------------public void solve () { move. Tower (total. Disks, 1, 3, 2); } © 2004 Pearson Addison-Wesley. All rights reserved 50

Towers. Of. Hanoi. java //-----------------------------// Moves the specified number of disks from one tower to // another by moving a subtower of n-1 disks out of the // way, moving one disk, then moving the subtower back. // Base case of 1 disk. //-----------------------------private void move. Tower (int num. Disks, int start, int end, int temp) { if (num. Disks == 1) move. One. Disk (start, end); else { move. Tower (num. Disks-1, start, temp, end); move. One. Disk (start, end); move. Tower (num. Disks-1, temp, end, start); } } © 2004 Pearson Addison-Wesley. All rights reserved 51

Towers. Of. Hanoi. java //-----------------------------// Prints instructions to move one disk from the specified // start tower to the specified end tower. //-----------------------------private void move. One. Disk (int start, int end) { System. out. println ("Move one disk from " + start + " to " + end); } } public class Solve. Towers { //-----------------------------// Creates a Towers. Of. Hanoi puzzle and solves it. //-----------------------------public static void main (String[] args) { Towers. Of. Hanoi towers = new Towers. Of. Hanoi (4); towers. solve(); } } © 2004 Pearson Addison-Wesley. All rights reserved 52

Summary • Chapter 11 has focused on: § § thinking in a recursive manner programming in a recursive manner the correct use of recursion examples © 2004 Pearson Addison-Wesley. All rights reserved 53
- Slides: 53