Chapter 7 Arithmetic Operations and Circuits 1 Objectives

Chapter 7 Arithmetic Operations and Circuits 1

Objectives You should be able to: Perform the four binary arithmetic functions: addition, subtraction, multiplication, and division. n Convert positive and negative numbers to signed two’s-complement notation. n Perform two’s-complement, hexadecimal, and BCD arithmetic. n 2

Objectives (Continued) n Explain the design and operation of a halfadder and a full-adder circuit. n Use full-adder ICs to implement arithmetic circuits. n Explain the operation of a two’s-complement adder/subtractor circuit and a BCD adder circuit. n Explain the function of an arithmetic logic unit (ALU). n Implement arithmetic functions in FPGAs using VHDL. 3

Binary Arithmetic n Addition When the sum exceeds 1, carry a 1 over to the next-more-significant column. n 0 + 0 = 0 carry 0 n 0 + 1 = 1 carry 0 n 1 + 0 = 1 carry 0 n 1 + 1 = 0 carry 1 n 5
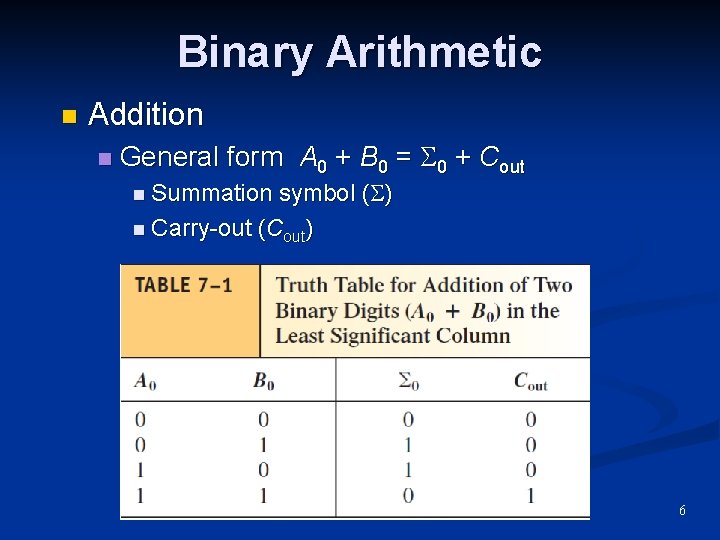
Binary Arithmetic n Addition n General form A 0 + B 0 = 0 + Cout symbol ( ) n Carry-out (Cout) n Summation 6

Binary Arithmetic n Carry-out is added to the next-moresignificant column as a carry-in. 7

Binary Arithmetic n Subtraction 0=0 n 0 1 = 1 n 1 0 = 1 n 1 1 = 0 n 0 borrow 1 borrow 0 8

Binary Arithmetic n Subtraction n General form A 0 B 0 = R 0 + Bout n Remainder n Borrow is R 0 is Bout 9

Binary Arithmetic n Subtraction n When A 0 borrows from its left, A 0 increases by 210. 10

Binary Arithmetic n Multiplication Multiply the 20 bit of the multiplier times the multiplicand. n Multiply the 21 bit of the multiplier times the multiplicand. Shift the result one position to the left. n Repeat step 2 for the 22 bit of the multiplier, and for all remaining bits. n Take the sum of the partial products to get the final product. n 11

Binary Arithmetic n Multiplication n Very similar to multiplying decimal numbers. 12

Binary Arithmetic n Division n The same as decimal division. n This process is illustrated in Example 7 -4. 13

Example 7 -4 14

Example 7 -4 (Continued) 14

Two’s-Complement Representation Both positive and negative numbers can be represented n Binary subtraction is simplified n Groups of eight n Most significant bit (MSB) signifies positive or negative n 15

Two’s-Complement Representation n Sign bit 0 for positive n 1 for negative n n Range of positive numbers (8 -bit) n n 0000 to 0111 1111 (0 to 128) Range of negative numbers (8 -bit) n 1111 to 1000 0000 (-1 to -128) 16

Two’s-Complement Representation Decimal-to-Two’s-Complement Conversion n If a number is positive, the two’s complement number is the true binary equivalent. n If a number is negative: n Complement each bit (one’s complement) n Add 1 to the one’s complement n The sign bit will always end up a 1. n 18

Two’s-Complement Representation 18

Two’s-Complement Representation n Two’s-Complement-to-Decimal Conversion If the number is positive (sign bit = 0), convert directly n If the number is negative: n n Complement the entire two’s-complement number n Add 1 n Convert this to decimal n Result will be a negative number 19

Discussion Point n Convert the following numbers to two’scomplement form: 3510 -3510 n Convert the following two’s-complement number to decimal: 1101 20

Two’s-Complement Arithmetic n Addition n n Regular binary addition Subtraction Convert number to be subtracted to a negative two’s-complement number n Regular binary addition n Carry out of the MSB is ignored n 21

Discussion Point n Add the following numbers using two’s complement arithmetic: 19 + 27 18 – 7 21 – 13 59 – 96 22

Hexadecimal Arithmetic 4 binary bits represent a single hexadecimal digit n Addition n Add the digits in decimal n If sum is less than 16, convert to hexadecimal n Is sum is more than 16, subtract 16, convert to hexadecimal and carry 1 to the next-moresignificant column n 23

Example 7 -12

Hexadecimal Arithmetic n Subtraction When you borrow, the borrower increases by 16 n See example 7 -15 n 24

Example 7 -15 25

BCD Arithmetic Group 4 binary digits to get combinations for 10 decimal digits n Range of valid numbers 0000 to 1001 n Addition n Add as regular binary numbers n If sum is greater than 9 or if carry out generated: n n Add 6 (0110) saving any carry out 26

Arithmetic Circuits n n Only two inputs are of concern in the LSB column. More significant columns must include the carry-in from the previous column as a third input. 27

Arithmetic Circuits n The addition of the third input (Cin) is shown in the truth table below. 27

Arithmetic Circuits n Half-Adder No carry in (LSB column) n The 0 output is HIGH when A or B, but not both, is high. n n Exclusive-OR n function Cout is high when A and B are high. n AND function 28
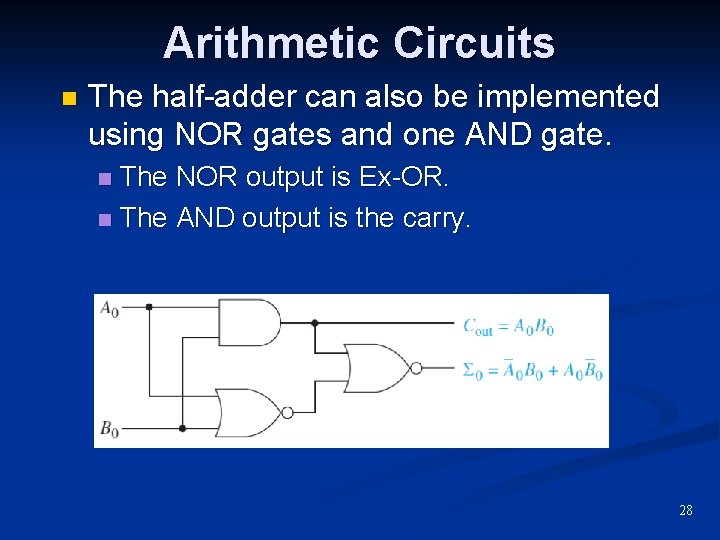
Arithmetic Circuits n The half-adder can also be implemented using NOR gates and one AND gate. The NOR output is Ex-OR. n The AND output is the carry. n 28

Arithmetic Circuits n Full-Adder Provides for a carry input n The 1 output is high when the 3 -bit input is odd. n n Even n parity generator Cout is high when any two inputs are high. n 3 AND gates and an OR 29
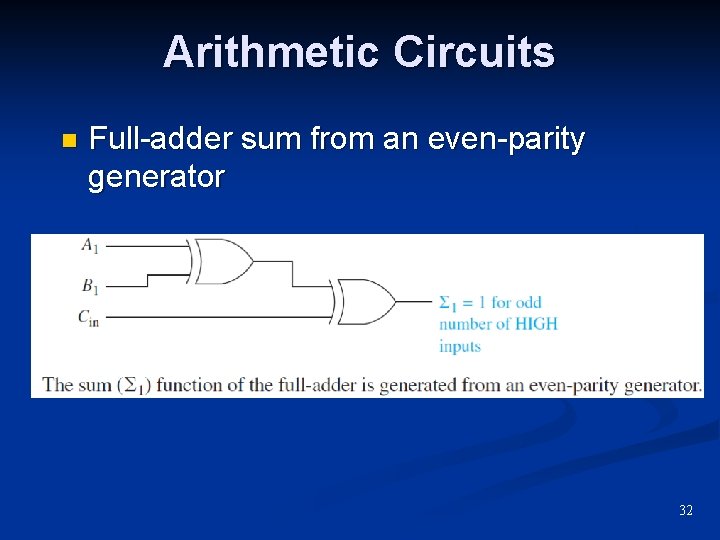
Arithmetic Circuits n Full-adder sum from an even-parity generator 32
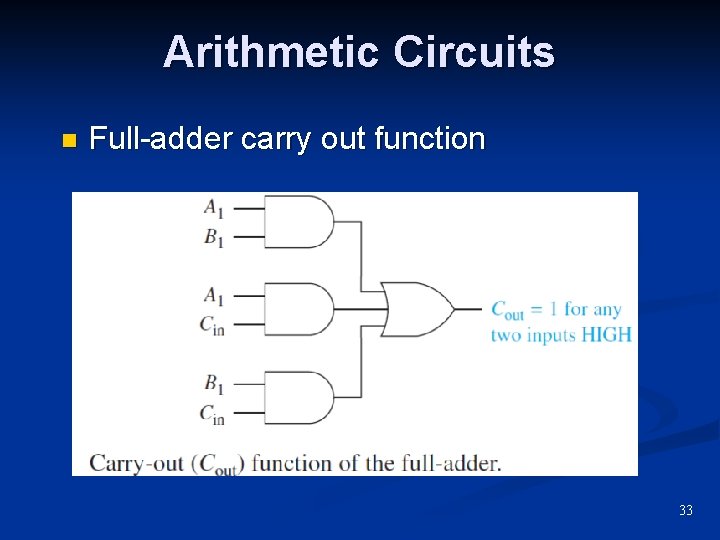
Arithmetic Circuits n Full-adder carry out function 33
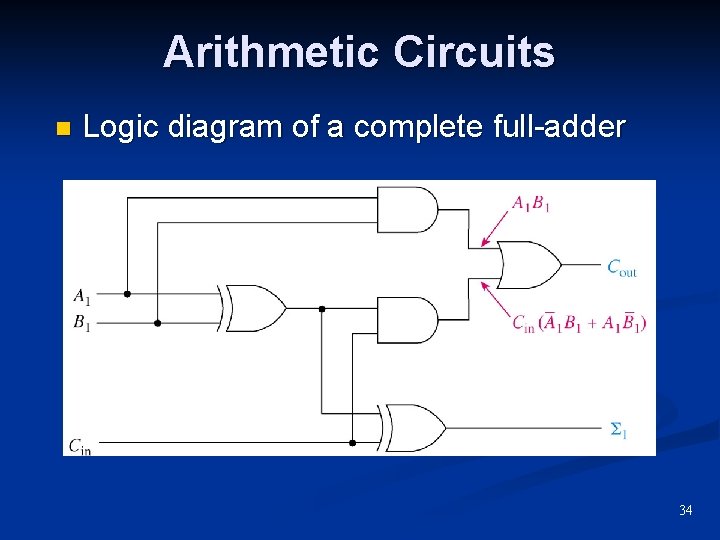
Arithmetic Circuits n Logic diagram of a complete full-adder 34

VHDL Description of a Full-Adder n Note the concurrent statements for the two logic circuits.
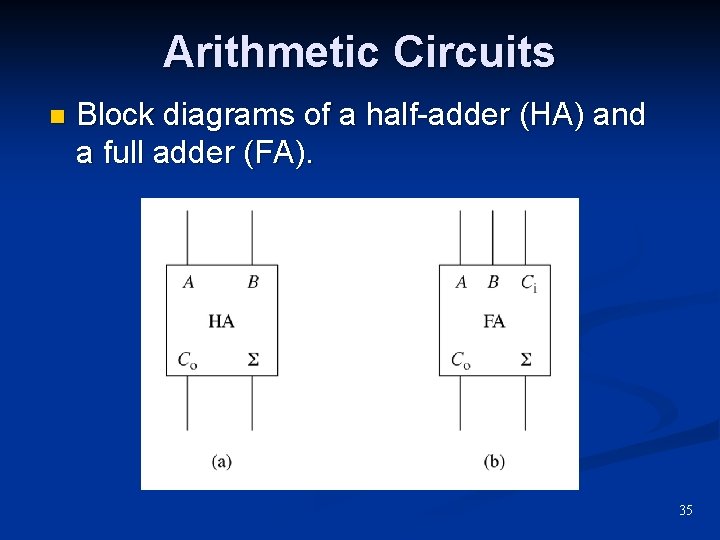
Arithmetic Circuits n Block diagrams of a half-adder (HA) and a full adder (FA). 35
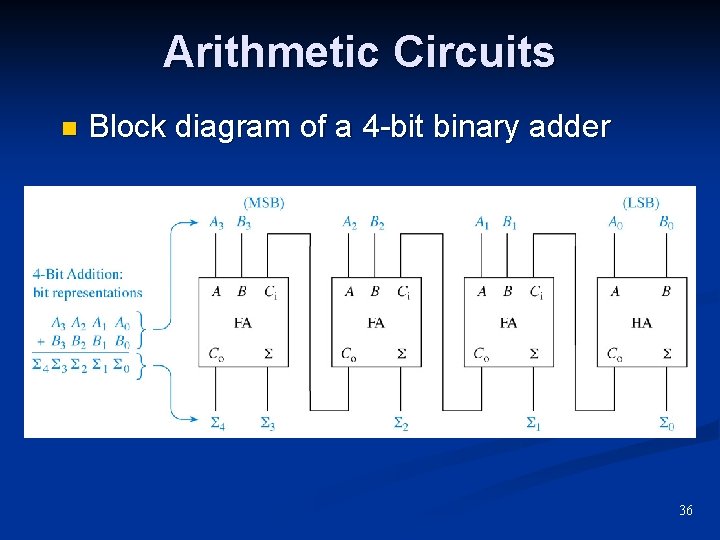
Arithmetic Circuits n Block diagram of a 4 -bit binary adder 36

Four-Bit Full-Adder ICs Four full-adders in a single package n Will add two 4 -bit binary words plus one carry input bit. n 37
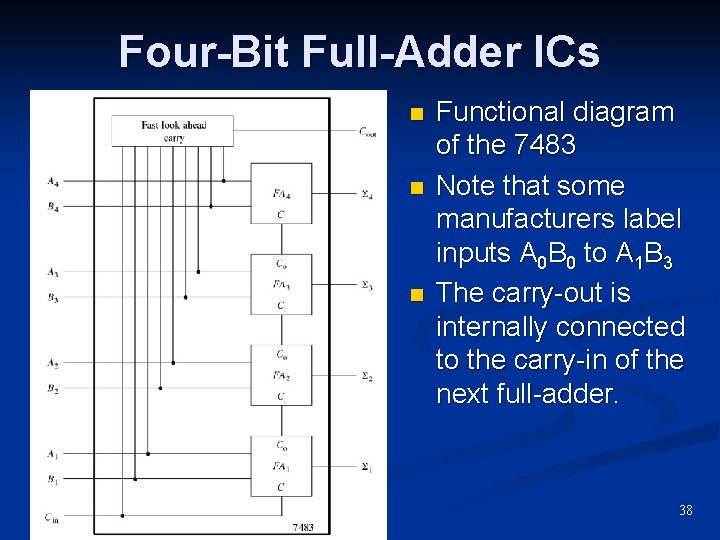
Four-Bit Full-Adder ICs n n n Functional diagram of the 7483 Note that some manufacturers label inputs A 0 B 0 to A 1 B 3 The carry-out is internally connected to the carry-in of the next full-adder. 38
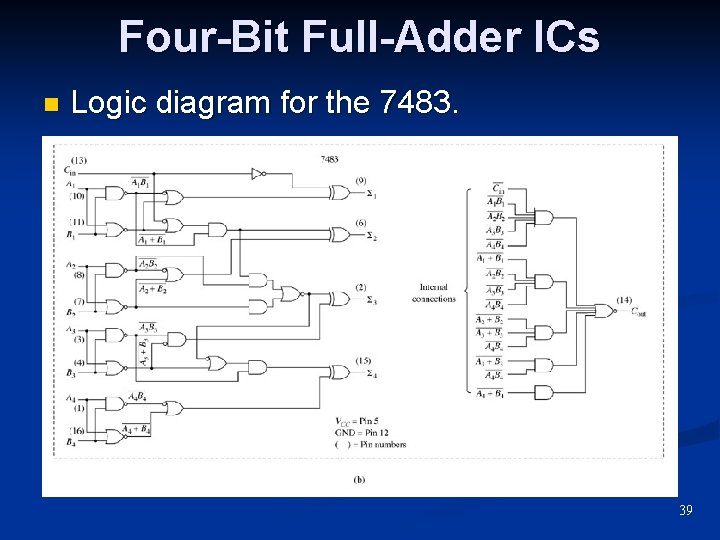
Four-Bit Full-Adder ICs n Logic diagram for the 7483. 39
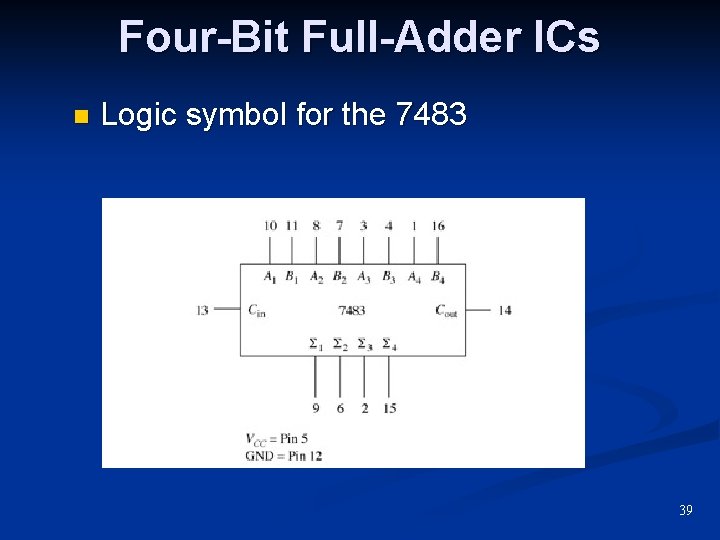
Four-Bit Full-Adder ICs n Logic symbol for the 7483 39

Four-Bit Full-Adder ICs n Fast-look-ahead carry Evaluates 4 low-order inputs n High-order bits added at same time n Eliminates waiting for propagation ripple n 40

VHDL Adders Using Integer Arithmetic n Uses arithmetic operator and integer data type Integer data type allows for values other than 1 and 0. n Integer range must be specified. n Software uses the range to determine the number of inputs required. n
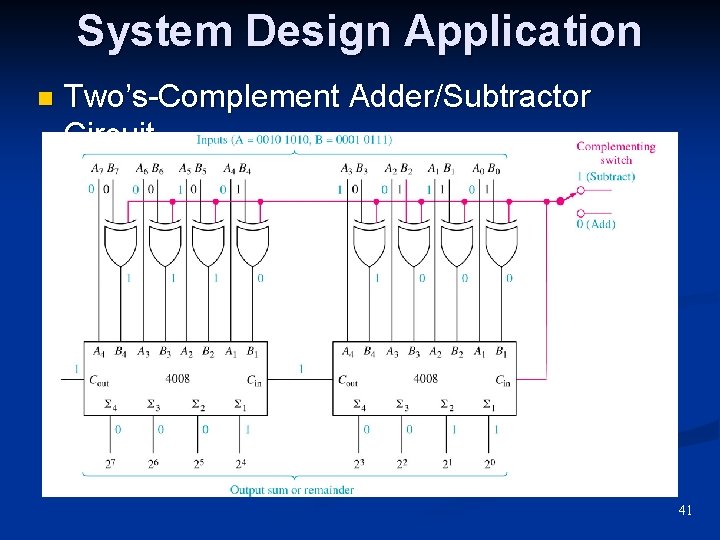
System Design Application n Two’s-Complement Adder/Subtractor Circuit 41

System Design Application n BCD Adder Circuit 42
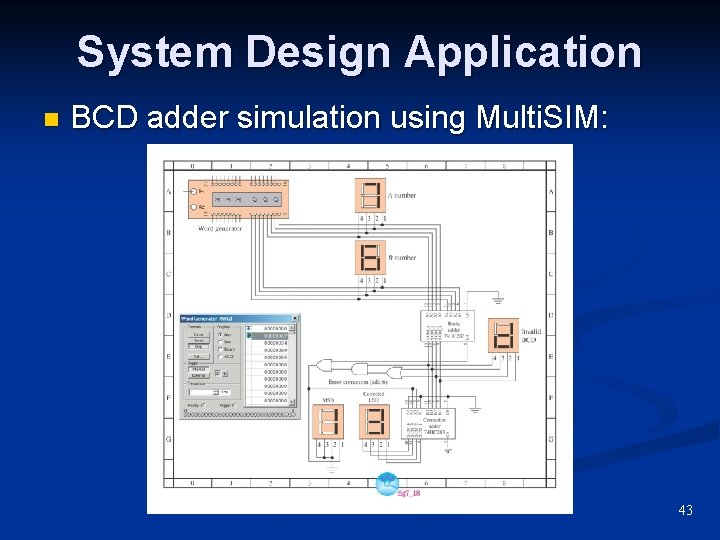
System Design Application n BCD adder simulation using Multi. SIM: 43

Arithmetic/Logic Units n n n The ALU is a multipurpose device Available in LSI package 74181 (TTL) 74 HC 181 (CMOS) Mode Control input n n Arithmetic (M = L) Logic (M = H) 44
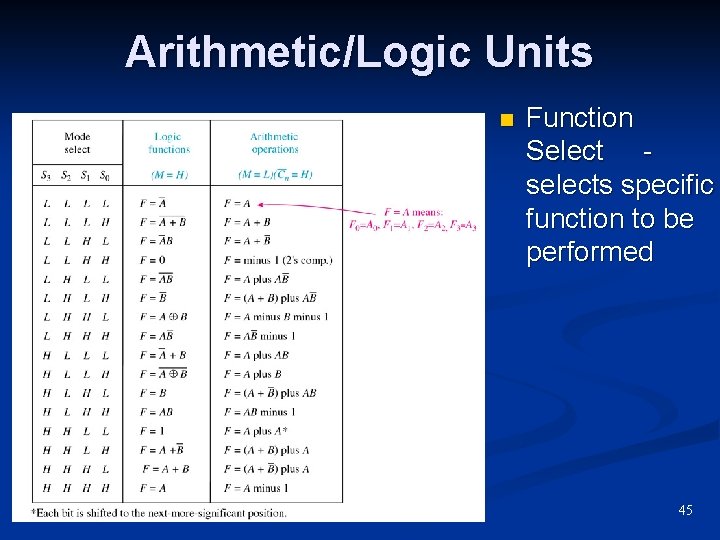
Arithmetic/Logic Units n Function Select selects specific function to be performed 45

FPGA Applications with VHDL and LPMs FPGA implementation using macrofunctions, VHDL, and LPMs. n Library of Parameterized Modules (LPMs) are a new form of design entry in Quarus II. n n Simplifies the design process for common systems like adders and ALUs. 46
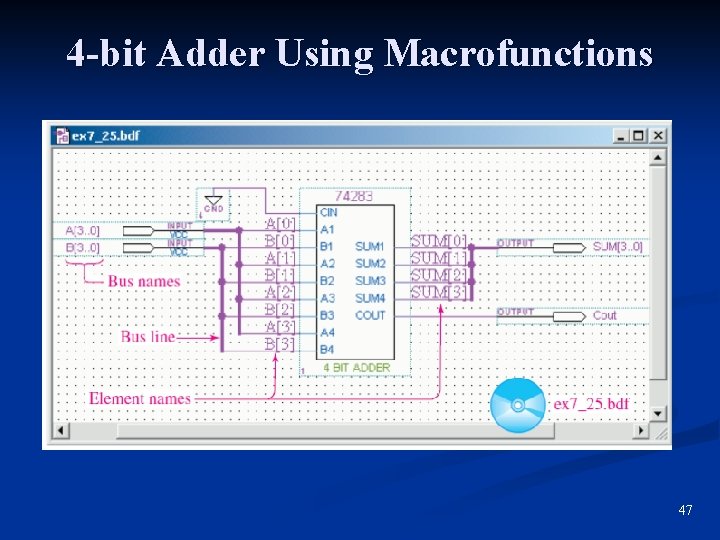
4 -bit Adder Using Macrofunctions 47
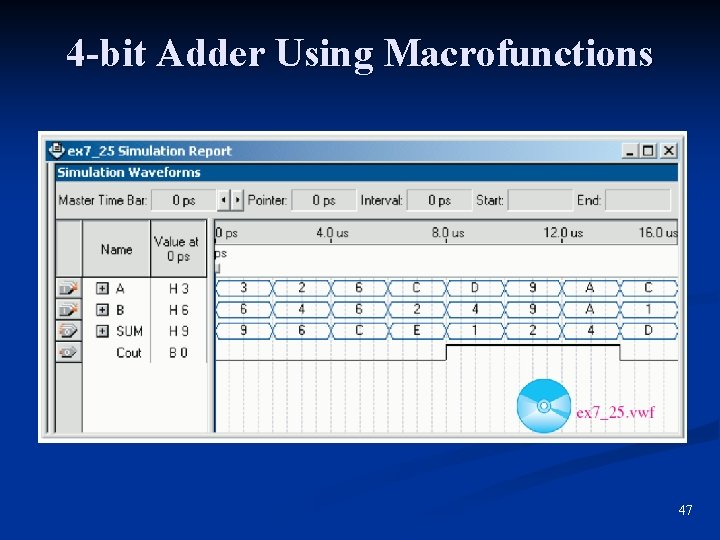
4 -bit Adder Using Macrofunctions 47

8 -Bit Adder/Subtractor in VHDL 47
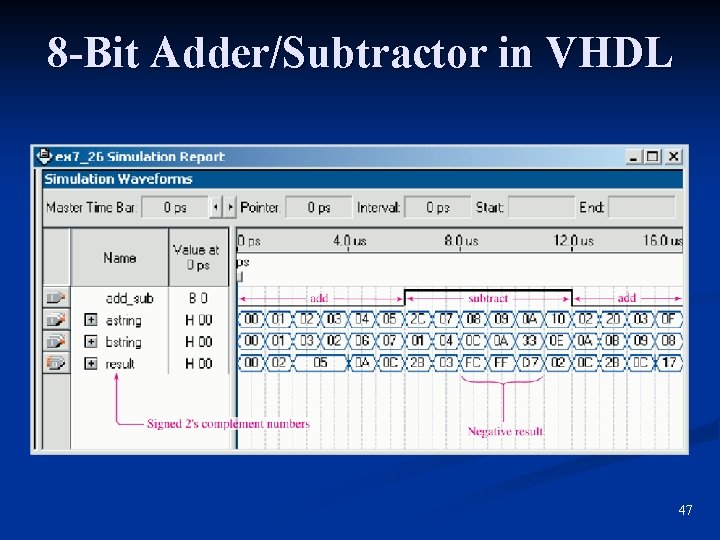
8 -Bit Adder/Subtractor in VHDL 47

BCD Correction Adder using IF-THEN-ELSE 47
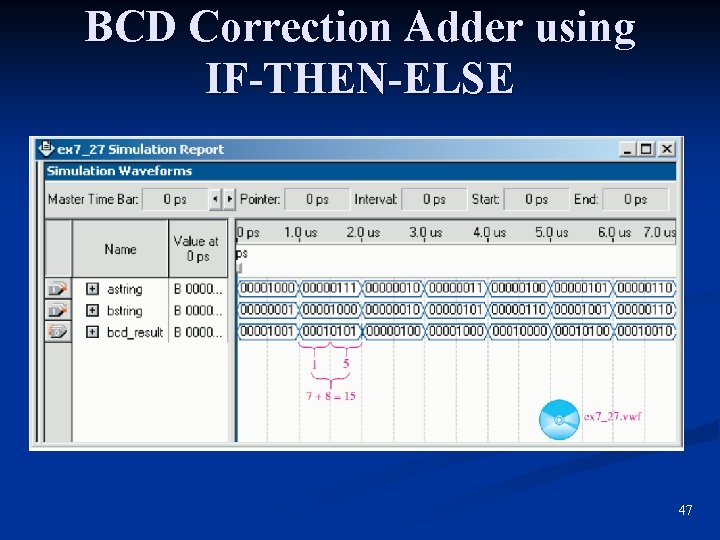
BCD Correction Adder using IF-THEN-ELSE 47
LPM Adder/Subtractor 47
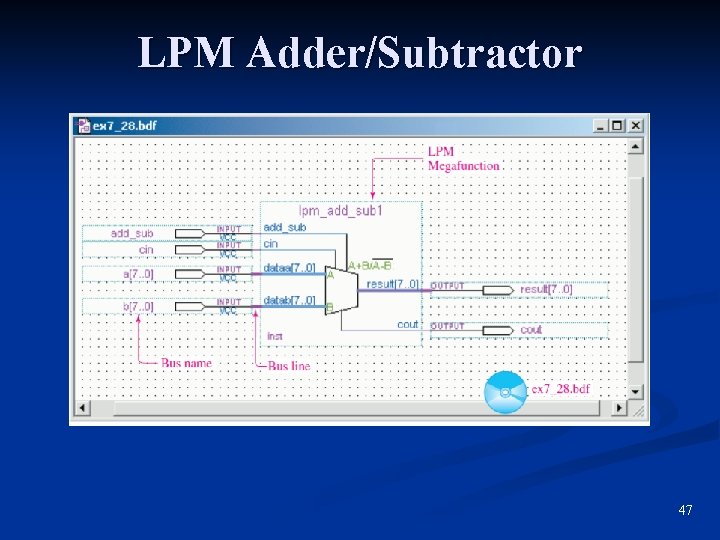
LPM Adder/Subtractor 47

LPM Adder/Subtractor 47

Summary The binary arithmetic functions of addition, subtraction, multiplication, and division can be performed bit-by-bit using several of the same rules of regular base 10 arithmetic. n The two’s-complement representation of binary numbers is commonly used by computer systems for representing positive and negative numbers. n 48

Summary Two’s-complement arithmetic simplifies the process of subtraction of binary numbers. n Hexadecimal addition and subtraction is often required for determining computer memory space and locations. n When performing BCD addition a correction must be made for sums greater than 9 or when a carry to the next more significant digit occurs. n 49

Summary Binary adders can be built using simple combinational logic circuits. n A half-adder is required for addition of the least significant bits n A full-adder is required for addition of the more significant bits. n 50

Summary Multibit full-adder ICs are commonly used for binary addition and two’s-complement arithmetic. n Arithmetic/logic units are multipurpose ICs capable of providing several different arithmetic and logic functions. n The logic circuits for adders can be described in VHDL using integer arithmetic. n 51

Summary The Quartus II software provides 7400 series macrofunctions and a Library of Parameterized Modules (LPMs) to ease in the design of complex digital systems. n Conditional assignments can be made using the IF-THEN-ELSE VHDL statements. n 51
- Slides: 64