Chapter 7 Angular Motion Things that turn have

Chapter 7 – Angular Motion Things that turn have both a linear velocity and an angular velocity.

Things that Turn - Examples tire on a car or bike film on a projector buckets on a waterwheel blade on a lawnmower teeth on a gear Earth around the sun propeller on an airplane seat on a Ferris wheel earth on its axis rope around a pulley fins on a fan or a windmill record on a record player can on a kitchen cabinet lazy susan drum/barrel in a clothes dryer horse on a Merry-Go-Round wind turbines

Rotational Displacement, Consider a disk that rotates from A to B: B Angular displacement : A can be measured in 1 rev = The best measure for rotation of rigid bodies is the

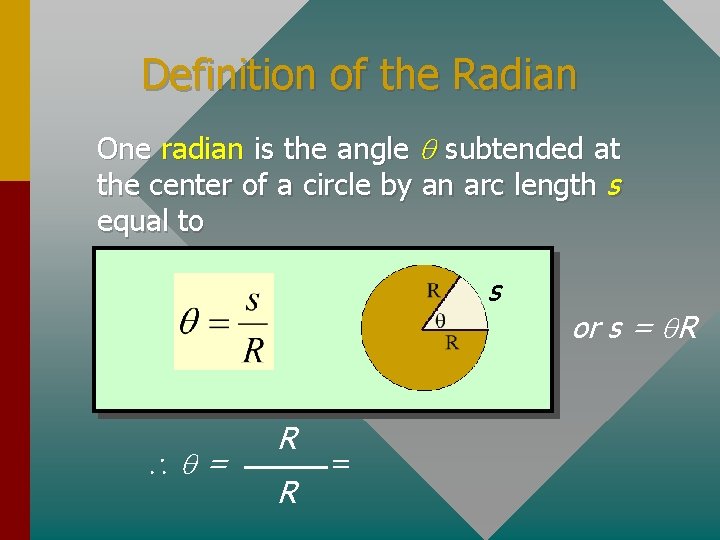
Definition of the Radian One radian is the angle subtended at the center of a circle by an arc length s equal to s = R R = or s = R

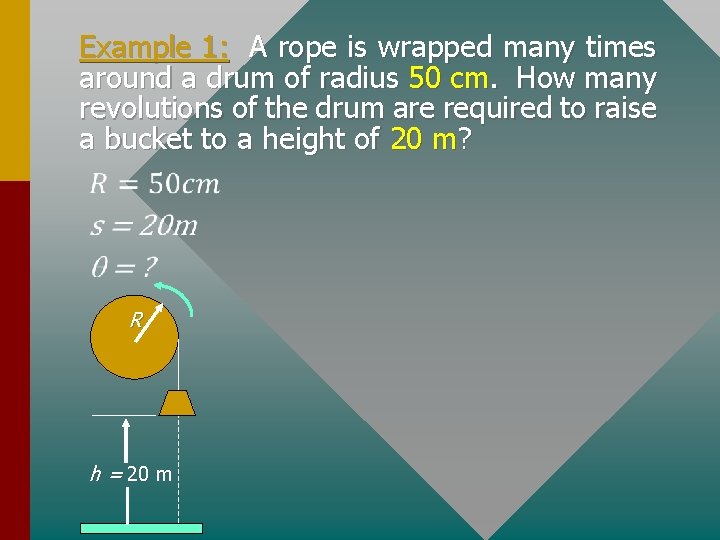
Example 1: A rope is wrapped many times around a drum of radius 50 cm. How many revolutions of the drum are required to raise a bucket to a height of 20 m? R h = 20 m

Example 2: A bicycle tire has a radius of 25 cm. If the wheel makes 400 rev, how far will the bike have traveled? R = 25 cm = 400 rev s=? s = R

Angular Velocity Angular velocity, w, is the rate of change in. (radians per second. ) w= t Angular velocity in rad/s. Angular velocity can also be given as the frequency of revolution, f (rev/s or rpm): w= Angular frequency f (rev/s).

Example 3: A rope is wrapped many times around a drum of radius 20 cm. What is the angular velocity of the drum if it lifts the bucket to 10 m in 5 s? R = 20 cm s = 10 m t = 5 s =? R h = 10 m

Example 4: In the previous example, what is the frequency of revolution (in rpm) for the drum? Recall that w = 10. 0 rad/s. R h = 10 m

Angular Acceleration Angular acceleration is the rate of change in. (Radians per sec. ) The angular acceleration can also be found from the change in frequency, as follows:

Example 5: The block is lifted from rest until the angular velocity of the drum is 16 rad/s after a time of 4 s. What is the average angular acceleration? o = 0 f = 16 rad/s t = 4 s =? R h = 20 m

Angular and Linear Speed From the definition of angular displacement: s = R Linear vs. angular displacement Linear speed = angular speed x radius

Angular and Linear Acceleration: From the velocity relationship we have: v = w. R Linear vs. angular velocity Linear accel. = angular accel. x radius

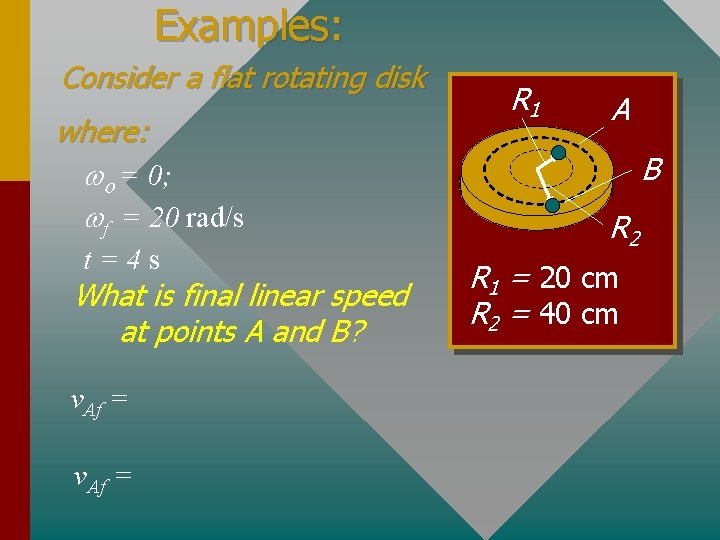
Examples: Consider a flat rotating disk where: wo = 0; wf = 20 rad/s t=4 s What is final linear speed at points A and B? v. Af = R 1 A B R 2 R 1 = 20 cm R 2 = 40 cm

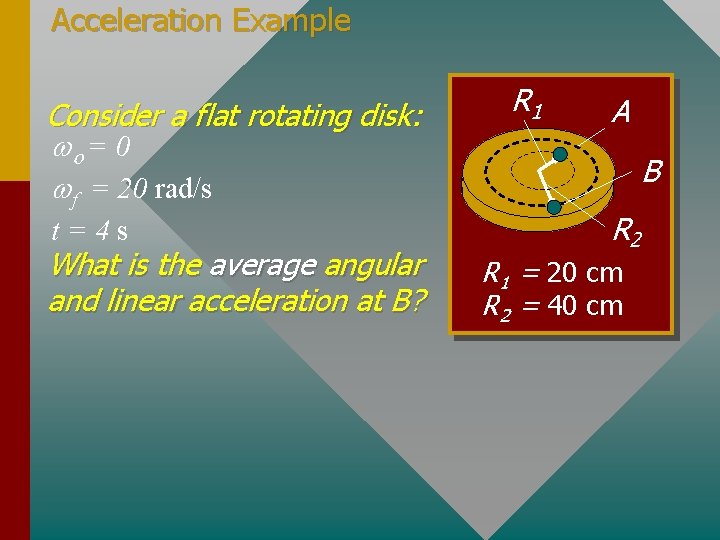
Acceleration Example Consider a flat rotating disk: wo = 0 wf = 20 rad/s t=4 s What is the average angular and linear acceleration at B? R 1 A B R 2 R 1 = 20 cm R 2 = 40 cm

Angular vs. Linear Parameters Recall the definition of linear acceleration a from kinematics. But, a = and v = , so that we may write: becomes Angular acceleration is the time rate of change in angular velocity.

Kinematic Equations: Converting Linear to Angular

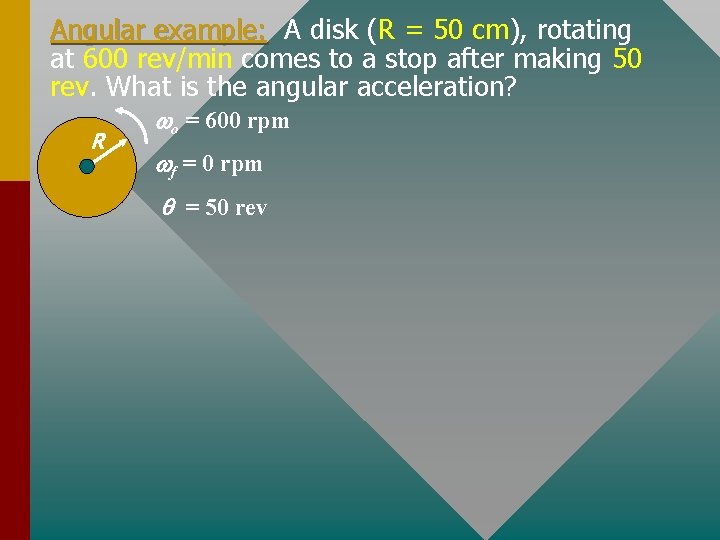
Angular example: A disk (R = 50 cm), rotating at 600 rev/min comes to a stop after making 50 rev. What is the angular acceleration? R wo = 600 rpm wf = 0 rpm q = 50 rev

Example 6: A drum is rotating clockwise initially at 100 rpm and undergoes a constant counterclockwise acceleration of 3 rad/s 2 for 2 s. What is the angular displacement? w = -100 rpm ; o +a t = 2 s R = +3 rad/s 2 =?

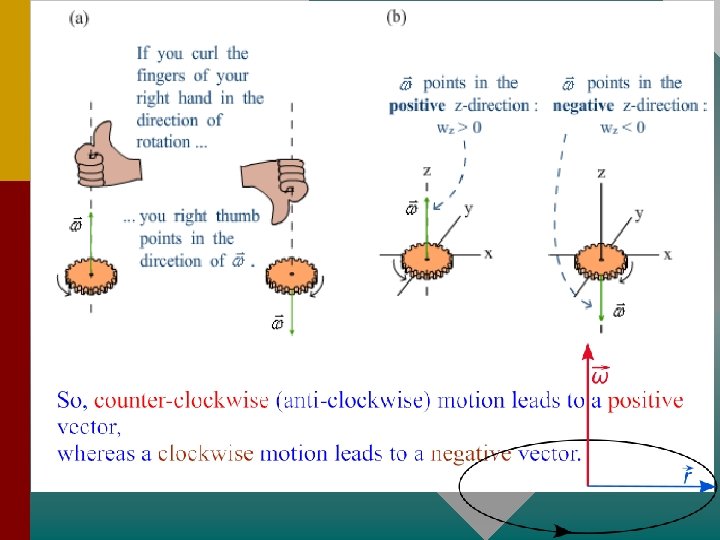
Vectors: θ, ω, & α are all vectors. But they are all going in a circular direction, so what straight line vector can represent their direction? We use the “ ". - Imagine the axis of rotation. - Now "grab" that axis with your fingers going in the same direction of motion. - Your points in the direction of that vector. (Yes, it is to the plane of motion !)

CONCLUSION and SUMMARY: