CHAPTER 7 Alternating Current Bridge School of Computer

CHAPTER 7 Alternating Current Bridge. School of Computer and Communication Engineering, Uni. MAP Prepared By: Amir Razif b. Jamil Abdullah EMT 113: V-2008 1

7. 0 AC Bridge. 7. 1 Introduction to AC Bridge. 7. 2 Similar-Angle Bridge. 7. 3 Maxwell-Wein Bridge. 7. 4 Opposite Angle Bridge. 7. 5 Wein Bridge. 7. 6 Scherning Bridge. 2

7. 1 Introduction to AC Bridge. þ AC bridges are used to measure inductance and capacitance. þ All the AC bridges are based on the Wheatstone bridge. þ In the AC bridge the bridge circuit consists of four impedances and an ac voltage source. þ The impedances can either be pure resistance or complex impedance. þ Other than measurement of unknown impedance, AC bridge are commonly used for shifting phase. Figure 7. 1: General AC Bridge Circuit. 3

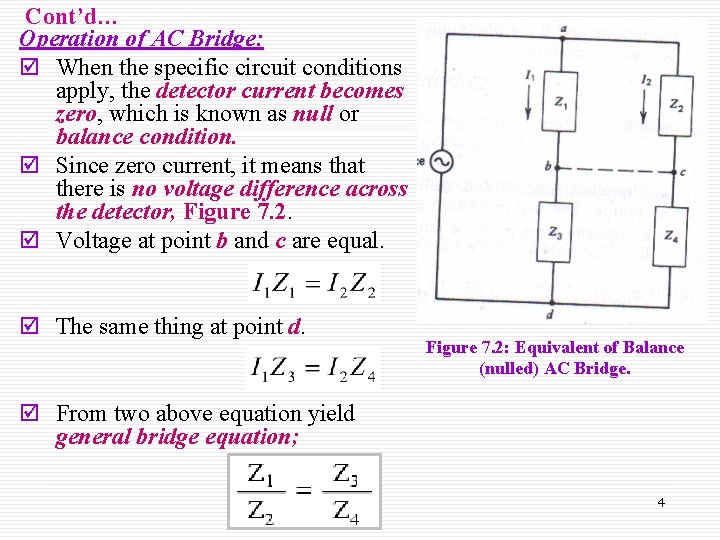
Cont’d… Operation of AC Bridge: þ When the specific circuit conditions apply, the detector current becomes zero, which is known as null or balance condition. þ Since zero current, it means that there is no voltage difference across the detector, Figure 7. 2. þ Voltage at point b and c are equal. þ The same thing at point d. Figure 7. 2: Equivalent of Balance (nulled) AC Bridge. þ From two above equation yield general bridge equation; 4

Cont’d… þ Figure 7. 3(a) and 7. 3 (b) is a simple AC Bridge circuit. Figure 7. 3: (a) and (b) are Simple AC Bridge Circuit. 5

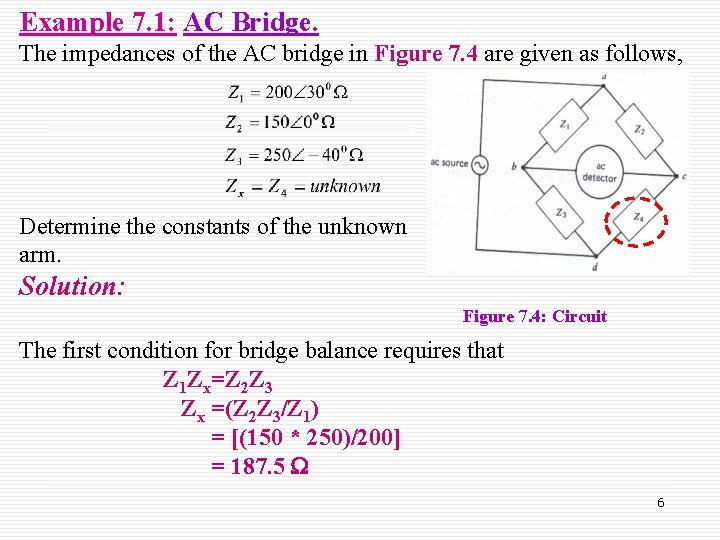
Example 7. 1: AC Bridge. The impedances of the AC bridge in Figure 7. 4 are given as follows, Determine the constants of the unknown arm. Solution: Figure 7. 4: Circuit The first condition for bridge balance requires that Z 1 Zx=Z 2 Z 3 Zx =(Z 2 Z 3/Z 1) = [(150 * 250)/200] = 187. 5 6

Cont’d… þ The secondition for balance requires that the sums of the phase angles of opposite arms be equal, equal þ 1+ x = 2 + 3 - 1 = 0 + (-40 o) – 30 o = -70 o The unknown impedance Zx, can be written as, þ This indicate that we are dealing with a capacitive element, possibly consisting of a series resistor and a capacitor. 7

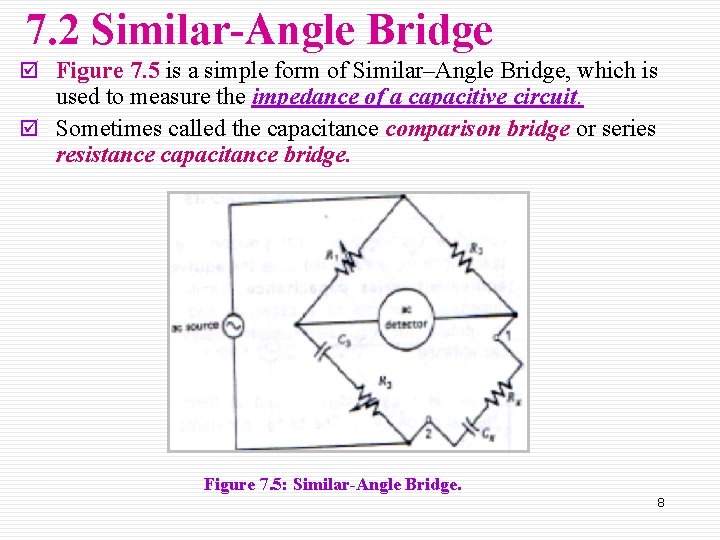
7. 2 Similar-Angle Bridge þ Figure 7. 5 is a simple form of Similar–Angle Bridge, which is used to measure the impedance of a capacitive circuit. þ Sometimes called the capacitance comparison bridge or series resistance capacitance bridge. Figure 7. 5: Similar-Angle Bridge. 8

Cont’d… þ The impedance of the arm can be written, þ Substitute in the balance equation, equation þ Further simplification, 9

7. 3 Maxwell-Wein Bridge þ It is used to measure unknown inductances with capacitance standard. þ Because the phase shifts of inductors and capacitors are exactly opposite each other, a capacitive impedance can balance out an inductive impedance if they are located in opposite legs of a bridge þ Figure 7. 6 is the Maxwell-Wein Bridge or sometimes called a Maxwell bridge. Figure 7. 6: Maxwell-Wein Bridge. 10

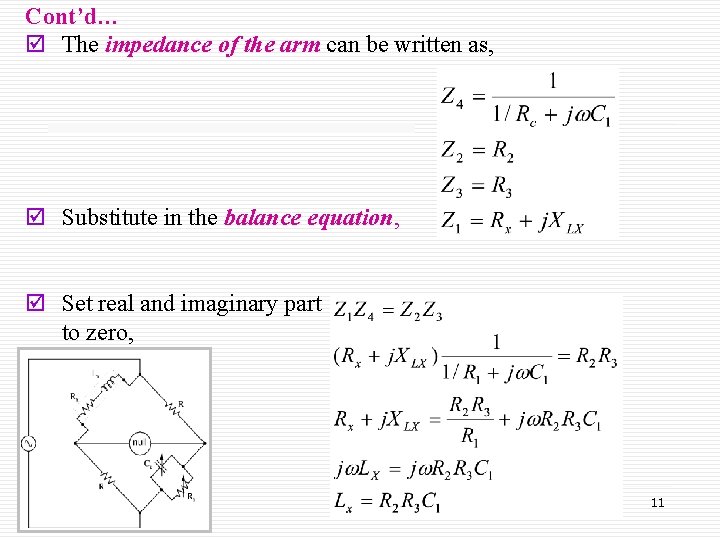
Cont’d… þ The impedance of the arm can be written as, þ Substitute in the balance equation, equation þ Set real and imaginary part to zero, 11

7. 4 Opposite-Angle Bridge þ This bridge is from Similar-Angle Bridge but the capacitance is replace with the inductance, inductance Figure 7. 7. þ It is used to measure inductance. þ Sometimes called a Hay bridge. Figure 7. 7: Opposite-Angle Bridge. 12

Cont’d… þ Equivalent series of inductance, þ Equivalent series of resistance, þ For the opposite angle bridge, it can be seen that the balance conditions depend on the frequency at which the measurement is 13 made.

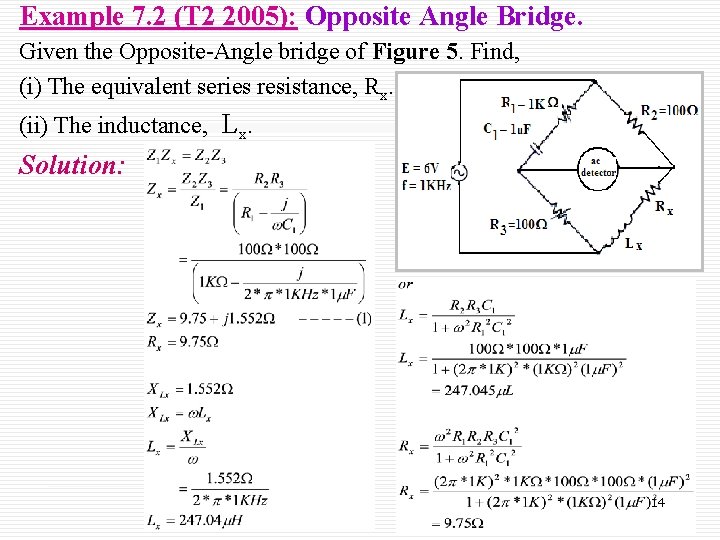
Example 7. 2 (T 2 2005): Opposite Angle Bridge. Given the Opposite-Angle bridge of Figure 5. Find, (i) The equivalent series resistance, Rx. (ii) The inductance, Lx. Solution: 14

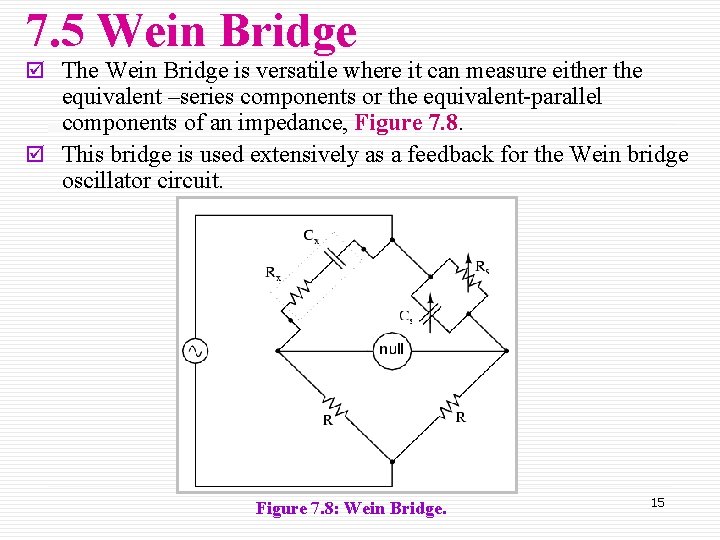
7. 5 Wein Bridge þ The Wein Bridge is versatile where it can measure either the equivalent –series components or the equivalent-parallel components of an impedance, Figure 7. 8. þ This bridge is used extensively as a feedback for the Wein bridge oscillator circuit. Figure 7. 8: Wein Bridge. 15

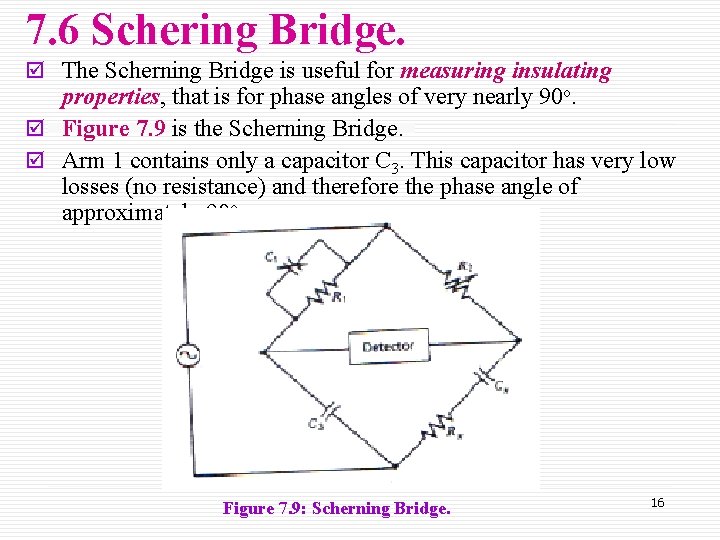
7. 6 Schering Bridge. þ The Scherning Bridge is useful for measuring insulating properties, that is for phase angles of very nearly 90 o. þ Figure 7. 9 is the Scherning Bridge. þ Arm 1 contains only a capacitor C 3. This capacitor has very low losses (no resistance) and therefore the phase angle of approximately 90 o. Figure 7. 9: Scherning Bridge. 16

Cont’d… þ The impedance of the arm of the Schering bridge is, þ Substitute the value, þ Expand, þ Equating the real and imaginary terms, 17

Example 7. 3: Schering Bridge. Find the equivalent series element for the unknown impedance of the Schering bridge network whose impedance measurements are to be made at null. R 1 = 470 k C 1 = 0. 01 m. F R 2 = 100 k C 3 = 0. 1 m. F Solution: Find Rx and Cx , q. 18