CHAPTER 7 Algebra Graphs Functions and Linear Systems

CHAPTER 7 Algebra: Graphs, Functions, and Linear Systems Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 7. 4, Slide 1

7. 4 Linear Inequalities in Two Variables Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 7. 4, Slide 2

Objectives 1. Graph a linear inequality in two variables. 2. Use mathematical models involving linear inequalities. 3. Graph a system of linear inequalities. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 7. 4, Slide 3

Linear Inequalities in Two Variables and Their Solutions If we change the symbol = in the equation Ax + By = C to >, <, ≥, or ≤, we obtain a linear inequality in two variables. For example, x + y < 2 and 3 x – 5 y ≥ 15 are linear inequalities in two variables. A solution of an inequality in two variables, x and y, is an ordered pair of real numbers such that when the xcoordinate is substituted for x and the y-coordinate is substituted for y in the inequality and we obtain a true statement. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 7. 4, Slide 4

The Graph of a Linear Inequality in Two Variables The graph of an inequality in two variables is the set of all points whose coordinates satisfy the inequality. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 7. 4, Slide 5

Example: Graphing a Linear Inequality in Two Variables Graph: 3 x – 5 y ≥ 15. Solution: Step 1 We need to graph 3 x – 5 y = 15. We can use intercepts to graph this line. We set y = 0 to find the x-intercept. We set x = 0 to find the y-intercept. 3 x – 5 y = 15 3 x – 5 · 0 = 15 3 x = 15 x=5 Copyright © 2015, 2011, 2007 Pearson Education, Inc. 3 x – 5 y = 15 3 · 0 – 5 y = 15 − 5 y = 15 y = − 3 Section 7. 4, Slide 6

Example continued The x-intercept is 5, so the line passes through (5, 0). The y-intercept is − 3, so the line passes through (0, − 3). Step 2 We choose (0, 0) as a test point. 3 x – 5 y ≥ 15 3 · 0 – 5 · 0 ≥ 15 0 – 0 ≥ 15 NOT TRUE! Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 7. 4, Slide 7
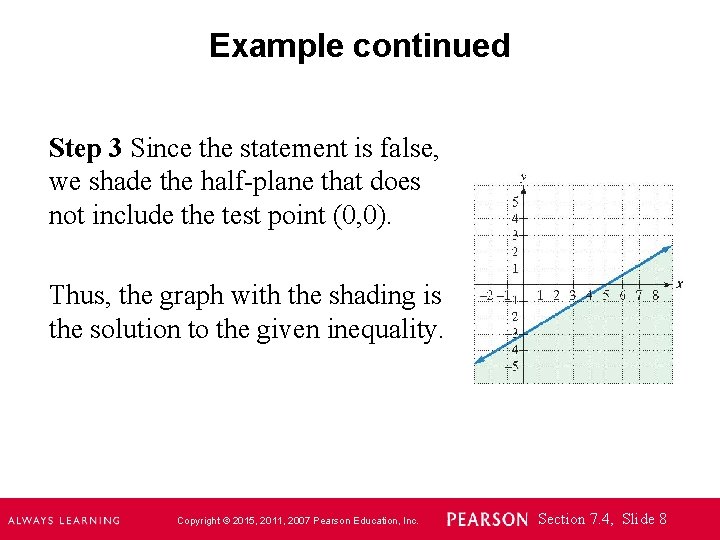
Example continued Step 3 Since the statement is false, we shade the half-plane that does not include the test point (0, 0). Thus, the graph with the shading is the solution to the given inequality. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 7. 4, Slide 8
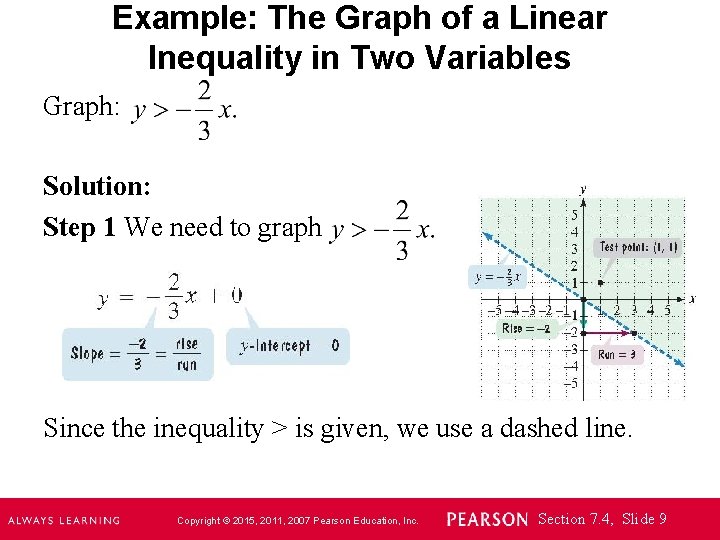
Example: The Graph of a Linear Inequality in Two Variables Graph: Solution: Step 1 We need to graph Since the inequality > is given, we use a dashed line. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 7. 4, Slide 9

Example continued Step 2 We choose a test point not on the line, (1, 1), which lies in the half-plane above the line. TRUE! Step 3 Since the statement is true, then we shade the half-plane that includes the test point (1, 1). Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 7. 4, Slide 10
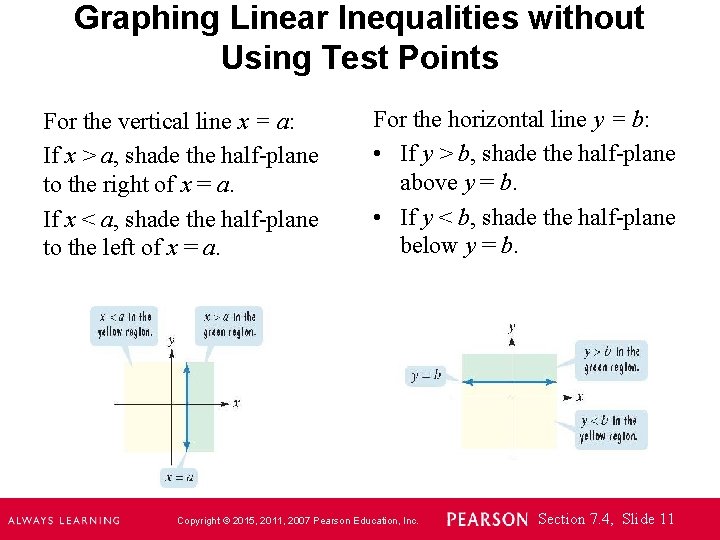
Graphing Linear Inequalities without Using Test Points For the vertical line x = a: If x > a, shade the half-plane to the right of x = a. If x < a, shade the half-plane to the left of x = a. For the horizontal line y = b: • If y > b, shade the half-plane above y = b. • If y < b, shade the half-plane below y = b. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 7. 4, Slide 11
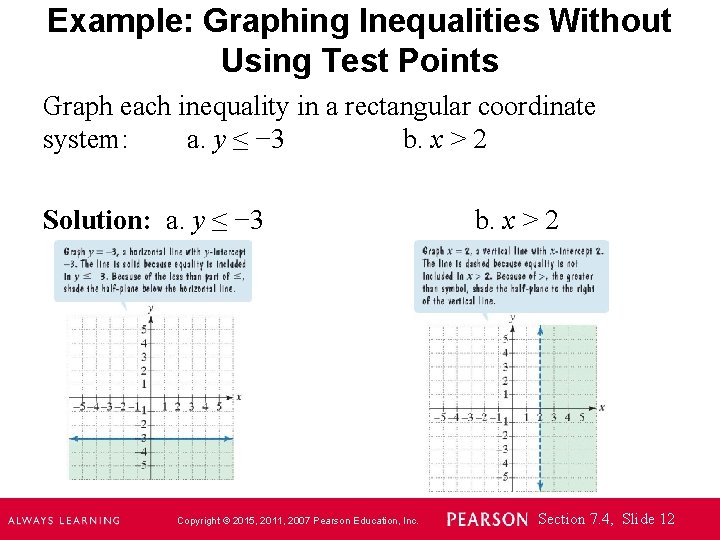
Example: Graphing Inequalities Without Using Test Points Graph each inequality in a rectangular coordinate system: a. y ≤ − 3 b. x > 2 Solution: a. y ≤ − 3 Copyright © 2015, 2011, 2007 Pearson Education, Inc. b. x > 2 Section 7. 4, Slide 12

Modeling with Systems of Linear Inequalities Just as two or more linear equations make up a system of linear equations, two or more linear inequalities make up a system of linear inequalities. A solution of a system of linear inequalities in two variables is an ordered pair that satisfies each inequalities in the system. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 7. 4, Slide 13

Graphing Systems of Linear Inequalities The solution set of a system of linear inequalities in two variables is the set of all ordered pairs that satisfy each inequality in the system. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 7. 4, Slide 14
Example: Graphing a System of Linear Inequalities Graph the solution set of the system: x–y<1 2 x + 3 y ≥ 12. Copyright © 2015, 2011, 2007 Pearson Education, Inc. Section 7. 4, Slide 15
- Slides: 15