Chapter 6 Vector Analysis April 16 Triple product

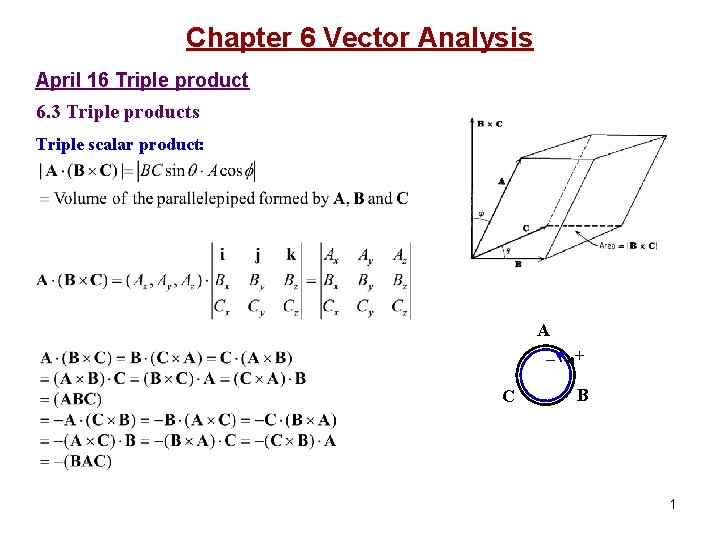
Chapter 6 Vector Analysis April 16 Triple product 6. 3 Triple products Triple scalar product: A _ C + B 1

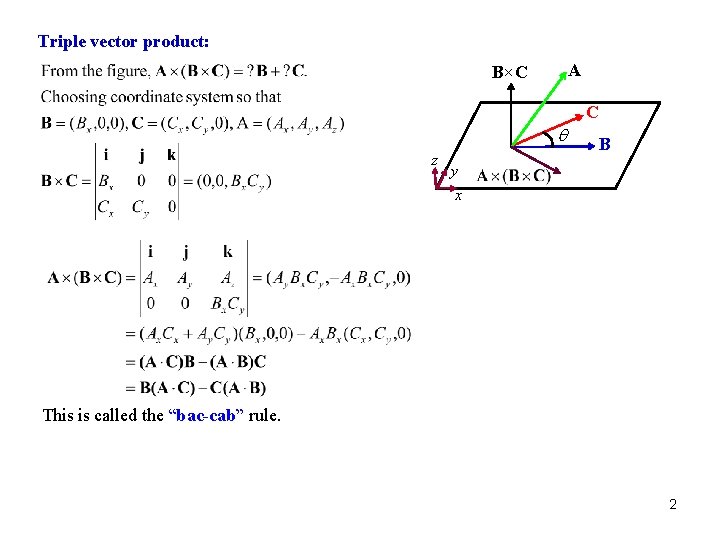
Triple vector product: A B×C C q z B y x This is called the “bac-cab” rule. 2

Example p 282. 1. Problems 3. 12 b. 3

Read: Chapter 6: 3 Homework: 6. 3. 9, 12, 19. Due: April 27 4

April 20 Gradient 6. 4 Differentiation of vectors Derivative of a vector: Derivative of vector products: y x Derivative in polar coordinates: 5

6. 6 Directional derivative; Gradient Directional derivative: The changing rate of a field along a certain direction. us r r 0 Gradient: 1. The gradient is in the direction along which the field increases the fastest. 2. The gradient is perpendicular to the equipotential surface f =constant. Examples p 292. 1, 3. 6

Read: Chapter 6: 4 -6 Homework: 6. 4. 2, 8; 6. 6. 1, 6, 7, 9. Due: April 27 7

April 23 Divergence and curl 6. 7 Some other expressions involving The operator: Vector function: Divergence: Curl: Laplacian: Vector identities involving : p 339. Examples p 297. 1, 2. 8

Physical meaning of divergence: Let V be the flux density (particles across a unit area in a unit time). x 0+dx is the net outflow flux per unit volume. Physical meaning of curl: Set the coordinate system so that z is along direction at the point (x 0, y 0, z 0 ). is the total circulation of V per unit area. 9

Read: Chapter 6: 7 Homework: 6. 7. 6, 7, 9, 13, 18. Due: May 4 10

April 25 Line integrals 6. 8 Line integrals B Line integral: Circulation: A Examples p 300. 1, 2 Conservative field: A field is said to be conservative if the path in the calculation. does not depend on Theorem: If F and its first partial derivatives are continuous in a simply connected region, then the following five statements are equivalent to each other. 1) 2) does not depend on the path. 3) is an exact differential. 4) 5) 11

Examples p 304. 3, 5. Examples p 306. 6. 12

Read: Chapter 6: 8 Homework: 6. 8. 9, 15, 17. Due: May 4 13

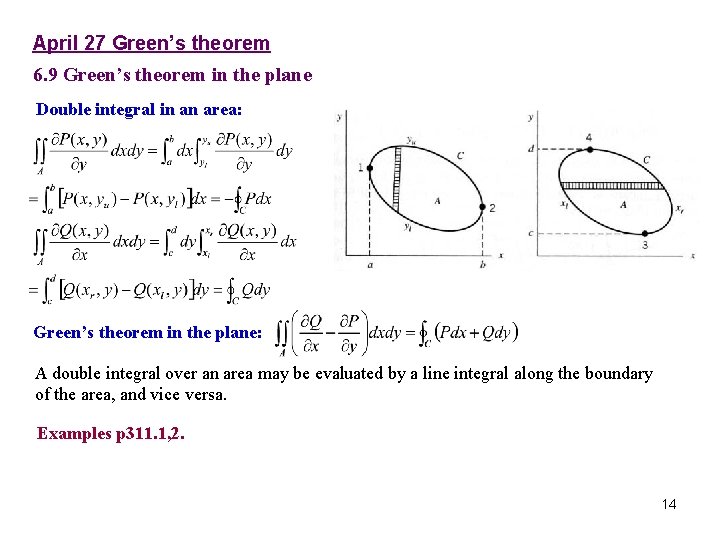
April 27 Green’s theorem 6. 9 Green’s theorem in the plane Double integral in an area: Green’s theorem in the plane: A double integral over an area may be evaluated by a line integral along the boundary of the area, and vice versa. Examples p 311. 1, 2. 14

Examples p 312. 3: Divergence theorem in two dimension: Examples p 312. 4: Stokes’ theorem in two dimension: 15

Read: Chapter 6: 9 Homework: 6. 9. 2, 3, 8, 10. Due: May 4 16

April 30 Gauss’ theorem 6. 10 The divergence and the divergence theorem Let r be the density, v be the velocity of water. The water flow in a unit time through a unit area that is perpendicular to v is given by V= r v, which is called flux density. The water flow rate through a surface with unit normal n is given by V·n. Physical meaning of divergence: Let V be the flux density. x 0+dx is the net rate of outflow flux per unit volume. 17

Time rate of the increase of mass per unit volume: Equation of continuity (when there is no sources): The divergence theorem (Gauss’ theorem): (Over a simply connected region. ) A volume integral may be evaluated by a closed surface integral on its boundary, and vice versa. Proof: For a differential cube, Sum over all differential cubes, at all interior surfaces will cancel, only the contributions from the exterior surfaces remain. Examples p 319. 18

Gauss’ law of electric field: For a single charge, For any charge distribution, From the divergence theorem, 19

Read: Chapter 6: 10 Homework: 6. 10. 3, 6, 7, 9. Due: May 9 20

May 2 Stokes’ theorem 6. 11 The curl and Stokes’ theorem Physical meaning of curl: Set the coordinate system so that z is along at the point (x 0, y 0, z 0 ). is the total circulation of V per unit area. 21

Stokes’ theorem: (Over a simply connected region. The surface does not need to be flat. ) A surface integral may be evaluated by a closed line integral at its boundary, and vice versa. Proof: Set the coordinate system so that x is along nds at an arbitrarily chosen point on the surface. Suppose the coordinates of that point is (x 0, y 0, z 0 ). Sum over all differential squares, at all interior lines will cancel, only the contributions from the exterior lines remain. Corollary: Examples p 328. 1. 22

Ampere’s law: 23

Read: Chapter 6: 11 Homework: 6. 11. 6, 10, 12, 14. Due: May 9 24