Chapter 6 Units Dimensions Objectives z Know the

Chapter 6 Units & Dimensions

Objectives z Know the difference between units and dimensions z Understand the SI, USCS (U. S. Customary System, or British Gravitational System), and AES (American Engineering) systems of units z Know the SI prefixes from nano- to gigaz Understand apply the concept of dimensional homogeneity

Objectives z. What is the difference between an absolute and a gravitational system of units? z. What is a coherent system of units? z. Apply dimensional homogeneity to constants and equations.

Introduction z. France in 1840 legislated official adoption of the metric system and made its use be mandatory z. In U. S. , in 1866, the metric system was made legal, but its use was not compulsory

Engineering Metrology z. Measurement of dimensions y. Length y. Thickness y. Diameter y. Taper y. Angle y. Flatness yprofiles

Measurement Standard z. Inch, foot; based on human body z 4000 B. C. Egypt; King’s Elbow=0. 4633 m, 1. 5 ft, 2 handspans, 6 hand-widths, 24 finger-thickness z. AD 1101 King Henry I yard (0. 9144 m) from his nose to the tip of his thumb z 1528 French physician J. Fernel distance between Paris and Amiens

Measurement Standard z 1872, Meter (in Greek, metron to measure)- 1/10 of a millionth of the distance between the North Pole and the equator z. Platinum (90%)-iridium (10%) X-shaped bar kept in controlled condition in Paris 39. 37 in z. In 1960, 1, 650, 763. 73 wave length in vacuum of the orange light given off by electrically excited krypton 86.

Dimensions & Units z Dimension - abstract quantity (e. g. length) y Dimensions are used to describe physical quantities y Dimensions are independent of units z Unit - a specific definition of a dimension based upon a physical reference (e. g. meter)

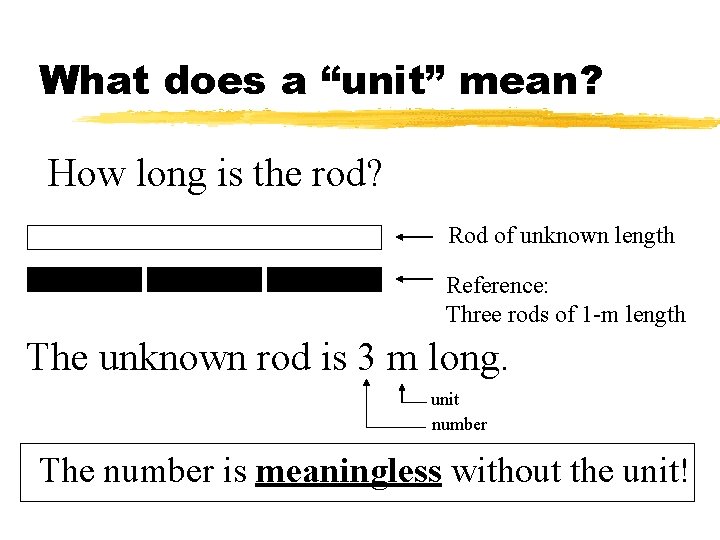
What does a “unit” mean? How long is the rod? Rod of unknown length Reference: Three rods of 1 -m length The unknown rod is 3 m long. unit number The number is meaningless without the unit!

How do dimensions behave in mathematical formulae? Rule 1 - All terms that are added or subtracted must have same dimensions All have identical dimensions

How do dimensions behave in mathematical formulae? Rule 2 - Dimensions obey rules of multiplication and division

How do dimensions behave in mathematical formulae? Rule 3 - In scientific equations, the arguments of “transcendental functions” must be dimensionless. x must be dimensionless Exception - In engineering correlations, the argument may have dimensions Transcendental Function - Cannot be given by algebraic expressions consisting only of the argument and constants. Requires an infinite series

Dimensionally Homogeneous Equations An equation is said to be dimensionally homogeneous if the dimensions on both sides of the equal sign are the same.

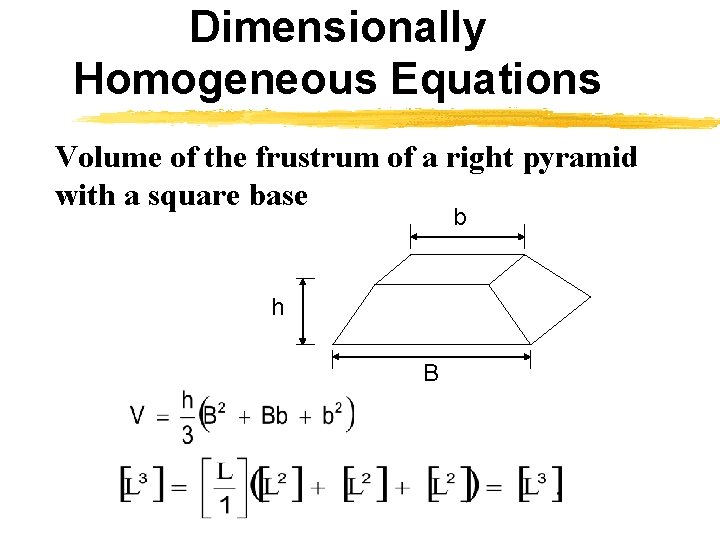
Dimensionally Homogeneous Equations Volume of the frustrum of a right pyramid with a square base b h B

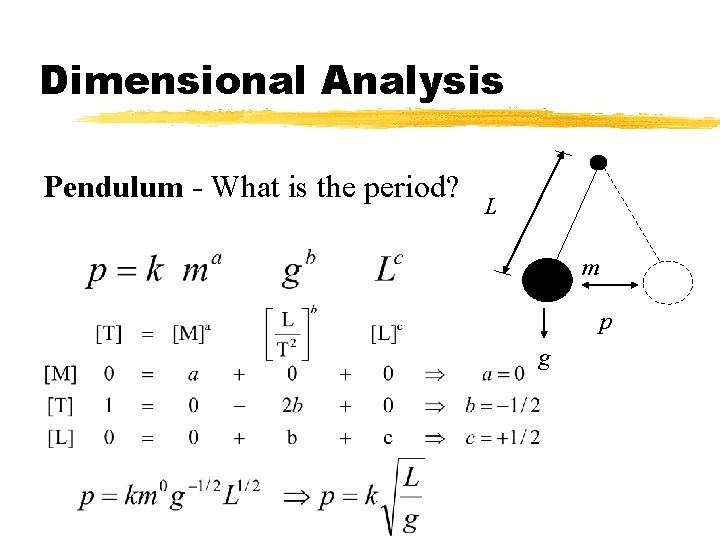
Dimensional Analysis Pendulum - What is the period? L m p g

Absolute and Gravitational Unit Systems z. Absolute system y. Dimensions used are not affected by gravity y. Fundamental dimensions L, T, M z. Gravitational System y. Widely used in engineering y. Fundamental dimensions L, T, F

Absolute and Gravitational Unit Systems [F] [M] [L] [T] Absolute — × × × Gravitational × — × × × = defined unit — = derived unit

Coherent and Noncoherent Unit Systems Coherent Systems - equations can be written without needing additional conversion factors Noncoherent Systems - equations need additional conversion factors Conversion Factor

Noncoherent Unit Systems z. One pound-force (lbf) is the effort required to hold a one pound-mass elevated in a gravitational field where the local acceleration of gravity is 32. 147 ft/s 2 z. Constant of proportionality gc should be used if slug is not used for mass zgc=32. 147 lbm. ft/lbf. s 2

Example of Noncoherent Unit Systems z. If a child weighs 50 pounds, we normally say its weight is 50. 0 lbm

Example of Noncoherent Unit Systems z. If a child weighs 50 pounds, on a planet where the local acceleration of gravity is 8. 72 ft/s 2

Noncoherent Systems Noncoherent [F] [M] [L] [T] × × × = defined unit — = derived unit The noncoherent system results when all four quantities are defined in a way that is not internally consistent (both mass and weight are defined historically)

Coherent System z. F=ma/gc; if we use slug for mass ygc= 1. 0 slug/lbf*1. 0 ft/s 2 z 1 z 1 slug=32. 147 lbm slug times 1 ft/ s 2 gives 1 lbf lbm times 32. 147 ft/ s 2 gives 1 lbf kg times 1 m/ s 2 gives 1 N ygc= 1. 0 kg/N*1. 0 m/s 2

The International System of Units (SI) Fundamental Dimension Base Unit length [L] meter (m) mass [M] kilogram (kg) time [T] second (s) electric current [A] ampere (A) absolute temperature [q] luminous intensity [l] amount of substance [n] kelvin (K) candela (cd) mole (mol)

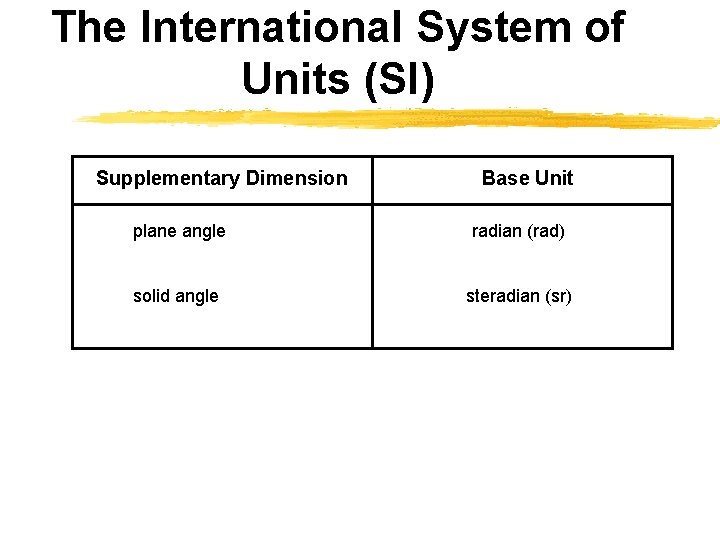
The International System of Units (SI) Supplementary Dimension Base Unit plane angle radian (rad) solid angle steradian (sr)

Fundamental Units (SI) Mass: “a cylinder of platinum-iridium (kilogram) alloy maintained under vacuum conditions by the International Bureau of Weights and Measures in Paris”

Fundamental Units (SI) Time: “the duration of 9, 192, 631, 770 periods (second) of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium-133 atom”

Fundamental Units (SI) Length or Distance: (meter) “the length of the path traveled by light in vacuum during a time interval of 1/299792458 seconds” photon Laser t=0 s 1 m t = 1/299792458 s

Fundamental Units (SI) Electric Current: (ampere) “that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross section, and placed one meter apart in a vacuum, would produce between these conductors a force equal to 2 × 10 -7 newtons per meter of length”

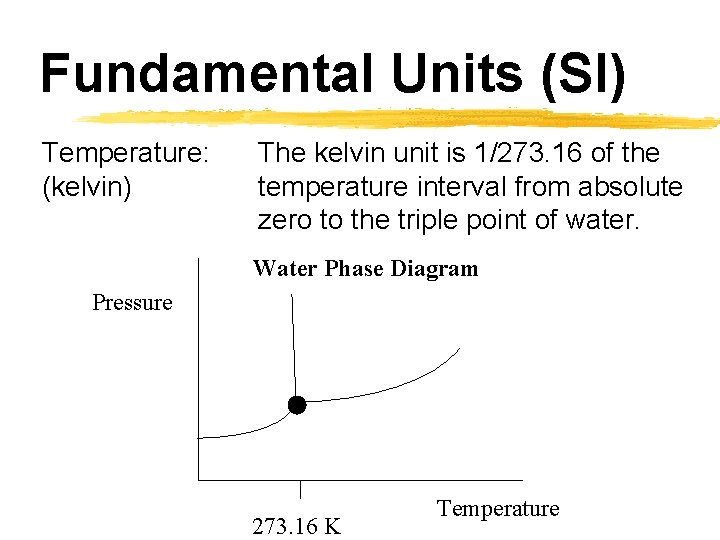
Fundamental Units (SI) Temperature: (kelvin) The kelvin unit is 1/273. 16 of the temperature interval from absolute zero to the triple point of water. Water Phase Diagram Pressure 273. 16 K Temperature

Fundamental Units (SI) AMOUNT OF “the amount of a substance that SUBSTANCE: contains as many elementary enti(mole) ties as there atoms in 0. 012 kilograms of carbon 12”

Fundamental Units (SI) LIGHT OR LUMINOUS INTENSITY: (candela) “the candela is the luminous intensity of a source that emits monochromatic radiation of frequency 540 × 1012 Hz and that has a radiant intensity of 1/683 watt per steradian. “ See Figure 13. 5 in Foundations of Engineering

Supplementary Units (SI) PLANE ANGLE: (radian) “the plane angle between two radii of a circle which cut off on the circumference an arc equal in length to the radius:

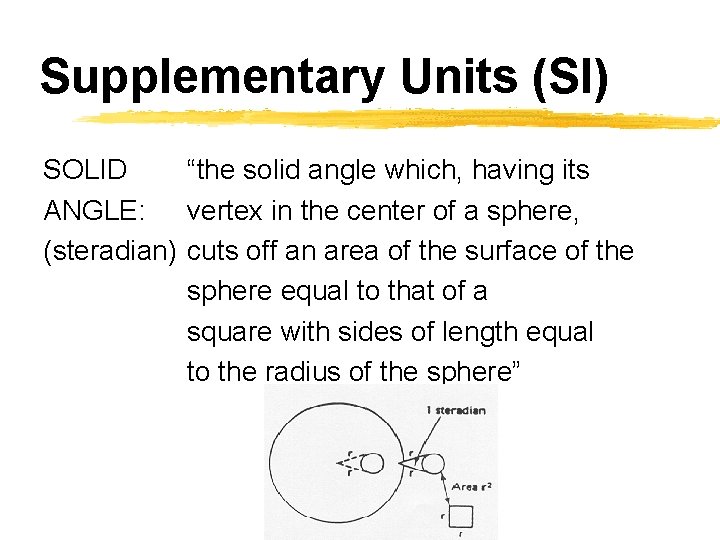
Supplementary Units (SI) SOLID “the solid angle which, having its ANGLE: vertex in the center of a sphere, (steradian) cuts off an area of the surface of the sphere equal to that of a square with sides of length equal to the radius of the sphere”

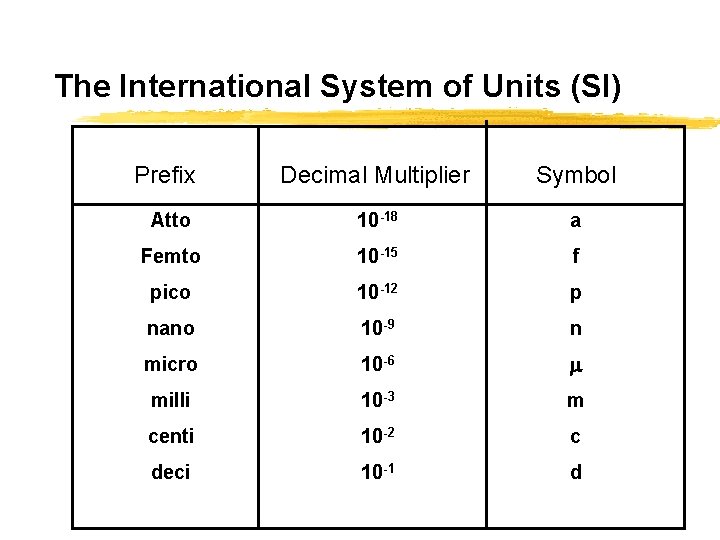
The International System of Units (SI) Prefix Decimal Multiplier Symbol Atto 10 -18 a Femto 10 -15 f pico 10 -12 p nano 10 -9 n micro 10 -6 m milli 10 -3 m centi 10 -2 c deci 10 -1 d

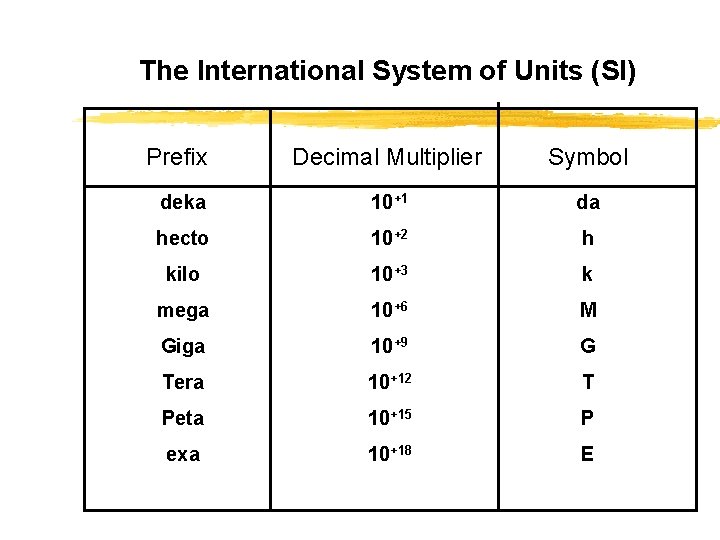
The International System of Units (SI) Prefix Decimal Multiplier Symbol deka 10+1 da hecto 10+2 h kilo 10+3 k mega 10+6 M Giga 10+9 G Tera 10+12 T Peta 10+15 P exa 10+18 E

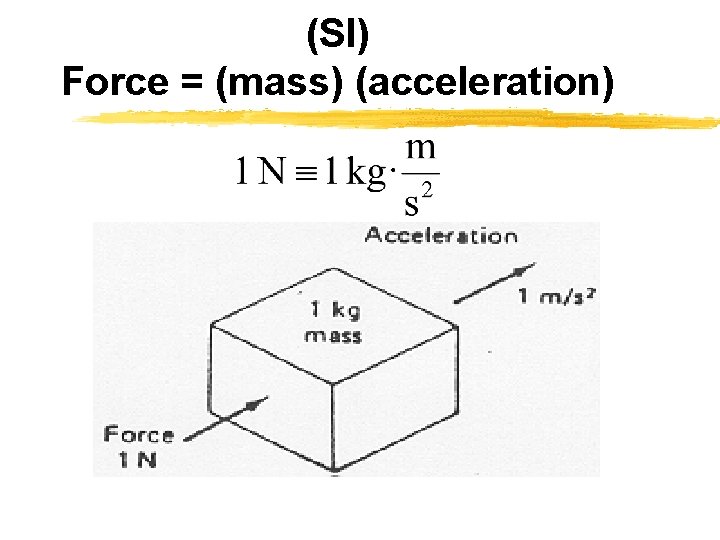
(SI) Force = (mass) (acceleration)

U. S. Customary System of Units (USCS) Fundamenal Dimension length [L] foot (ft) force [F] pound (lb) time [T] second (s) Derived Dimension mass [FT 2/L] Base Unit slug Definition

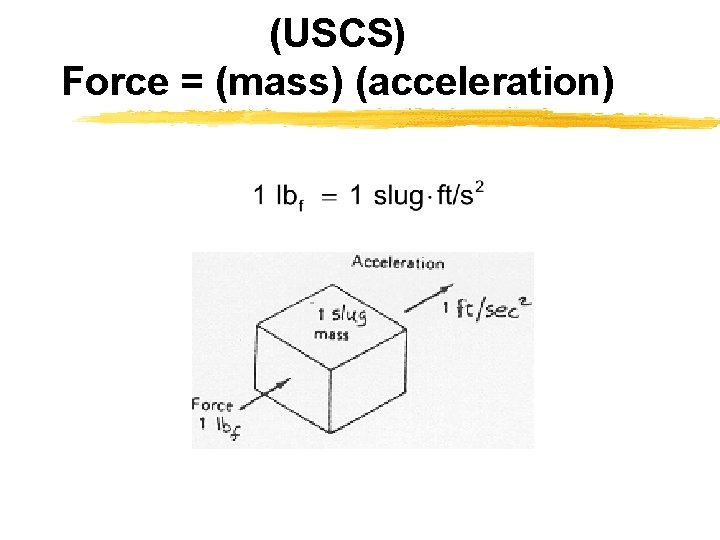
(USCS) Force = (mass) (acceleration)

American Engineering System of Units (AES) Fundamenal Dimension Base Unit length [L] foot (ft) mass [m] pound (lbm) force [F] pound (lbf) time [T] second (sec) electric change [Q] coulomb (C) absolute temperature [q] degree Rankine (o. R) luminous intensity [l] candela (cd) amount of substance [n] mole (mol)

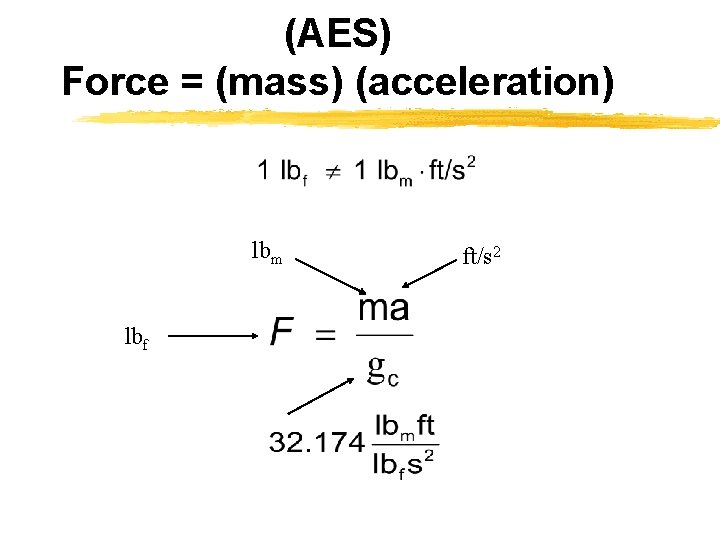
(AES) Force = (mass) (acceleration) lbm lbf ft/s 2

Rules for Using SI Units z. Periods are never used after symbols y. Unless at the end of the sentence y. SI symbols are not abbreviations z. In lowercase letter unless the symbol derives from a proper name ym, kg, s, mol, cd (candela) y. A, K, Hz, Pa (Pascal), C (Celsius)

Rules for Using SI Units z Symbols rather than self-styles abbreviations always should be used y. A (not amp), s (not sec) z An s is never added to the symbol to denote plural z A space is always left between the numerical value and the unit symbol y 43. 7 km (not 43. 7 km) y 0. 25 Pa (not 0. 25 Pa) y. Exception; 50 C, 5’ 6”

Rules for Using SI Units z There should be no space between the prefix and the unit symbols y. Km (not k m) ym. F (not m F) z When writing unit names, lowercase all letters except at the beginning of a sentence, even if the unit is derived from a proper name y. Farad, hertz, ampere

Rules for Using SI Units z. Plurals are used as required when writing unit names y. Henries (H; henry) y. Exceptions; lux, hertz, siemens z. No hyphen or space should be left between a prefix and the unit name y. Megapascal (not mega-pascal) y. Exceptions; megohm, kilohm, hetare

Rules for Using SI Units z. The symbol should be used in preference to the unit name because unit symbols are standardized y. Exceptions; ten meters (not ten m) y 10 m (not 10 meters)

Rules for Using SI Units z When writing unit names as a product, always use a space (preferred) or a hyphen ynewton meter or newton-meter z When expressing a quotient using unit names, always use the word per and not a solidus (slash mark /), which is reserved for use with symbols ymeter per second (not meter/second)

Rules for Using SI Units z. When writing a unit name that requires a power, use a modifier, such as squared or cubed, after the unit name ymillimeter squared (not square millimeter) z. When expressing products using unit symbols, the center dot is preferred y. N. m for newton meter

Rules for Using SI Units z When denoting a quotient by unit symbols, any of the follow methods are accepted form ym/s ym. s-1 yor y. M/s 2 is good but m/s/s is not y. Kg. m 2/(s 3. A) or kg. m 2. s-3. A-1 is good, not kg. m 2/s 3/A

Rules for Using SI Units z. To denote a decimal point, use a period on the line. When expressing numbers less than 1, a zero should be written before the decimal y 15. 6 y 0. 93

Rules for Using SI Units z. Separate the digits into groups of three, counting from the decimal to the left or right, and using a small space to separate the groups y 6. 513 824 y 76 851 y 7 434 y 0. 187 62

Conversions Between Systems of Units

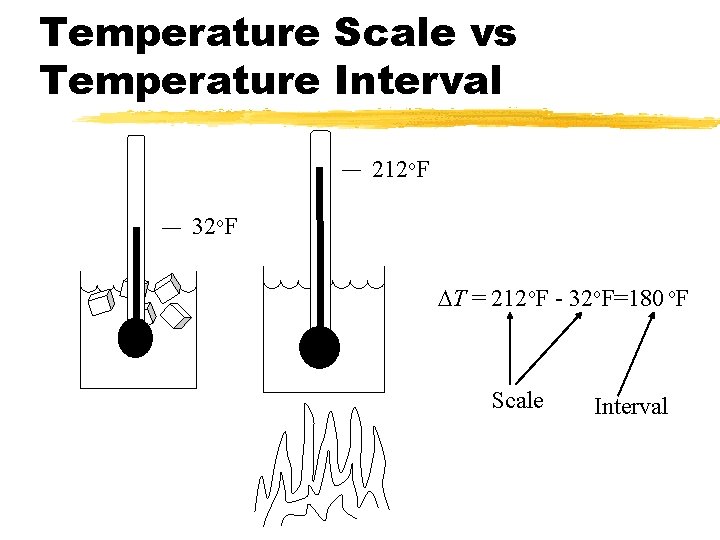
Temperature Scale vs Temperature Interval 212 o. F 32 o. F DT = 212 o. F - 32 o. F=180 o. F Scale Interval

Temperature Conversion Temperature Scale Temperature Interval Conversion Factors

Team Exercise 1 z The force of wind acting on a body can be computed by the formula: F = 0. 00256 Cd V 2 A where: F = wind force (lbf) Cd= drag coefficient (no units) V = wind velocity (mi/h) A = projected area(ft 2) z To keep the equation dimensionally homogeneous, what are the units of 0. 00256?

Team Exercise 2 Pressure loss due to pipe friction Dp = pressure loss (Pa) d = pipe diameter (m) f = friction factor (dimensionless) r = fluid density (kg/m 3) L = pipe length (m) v = fluid velocity (m/s) (1) Show equation is dimensionally homogeneous

Team Exercise 2 (con’t) (2) Find Dp (Pa) for d = 2 in, f = 0. 02, r = 1 g/cm 3, L = 20 ft, & v = 200 ft/min (3) Using AES units, find Dp (lbf/ft 2) for d = 2 in, f = 0. 02, r = 1 g/cm 3, L = 20 ft, & v = 200 ft/min

Formula Conversions Some formulas have numeric constants that are not dimensionless, i. e. units are hidden in the constant. As an example, the velocity of sound is expressed by the relation, where c = speed of sound (ft/s) T = temperature (o. R)

Formula Conversions Convert this relationship so that c is in meters per second and T is in kelvin. Step 1 - Solve for the constant Step 2 - Units on left and right must be the same

Formula Conversions Step 3 - Convert the units So where c = speed of sound (m/s) T = temperature (K) F

Team Exercise 3 The flow of water over a weir can be computed by: Q = 5. 35 LH 3/2 where: Q = volume of water (ft 3/s) L = length of weir(ft) H = height of water over weir (ft) Convert the formula so that Q is in gallons/min and L and H are measured in inches.