Chapter 6 Turing Machine Definition of the Turing

  • Slides: 12
Download presentation
Chapter 6 Turing Machine

Chapter 6 Turing Machine

Definition of the Turing Machine n There are some specific problems that cannot be

Definition of the Turing Machine n There are some specific problems that cannot be solved using a computer called undecidable or infractable problems n As a result, we use the TM to develop a theory of “undecidable” problems. n A very simple model of a computer called the TM, which is an abstract computing machine/device. This device is essentially a FA that has a single cells or squares on which it may read and write data and a finite state control.

Definition of the Turing Machine Finite State Control B B X 1 X 2

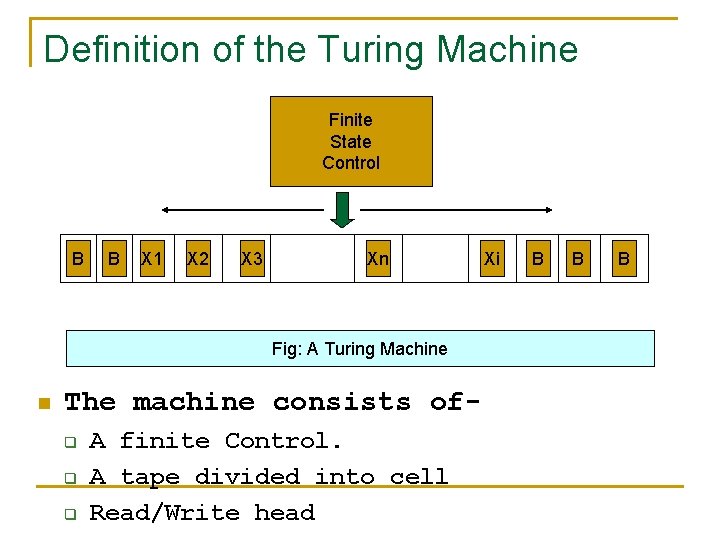
Definition of the Turing Machine Finite State Control B B X 1 X 2 X 3 Xn Fig: A Turing Machine n The machine consists ofq q q A finite Control. A tape divided into cell Read/Write head Xi B B B

Definition of the Turing Machine n Initially the input is placed on the tape,

Definition of the Turing Machine n Initially the input is placed on the tape, All other tape cells to the left and right initially hold a special symbol, not an input symbol blank (B). n The blank is a tape symbol. n Initially the tape head is at the following cell that holds the input. n A move of the TM meansq q q Change state Write a tape symbol in the cell scanned. Move the tape head left or right.

The formal notation of Turing Machine M=(Q, ∑, Γ, ∂, q 0, B, F)

The formal notation of Turing Machine M=(Q, ∑, Γ, ∂, q 0, B, F) Q ∑ Γ ∂ : A finite set of states of the finite control. : A finite set of input symbols. : A complete set of tape symbols. : The transition function. Here ∂ takes as arguments ∂(q, X) are a state q and a tape symbol X, The value of ∂(q, X) is a triple (p, Y, D), where p next state in Q Y is the symbol in Γ, replacing whatever symbol was there D direction either L(Left) or R(Right). q 0 : The start state, member of Q. B : The Blank symbol. F : The set of accepting states, subset of Q.

Example of Turing Machine n Design a TM which accept the language L(M)={0 n

Example of Turing Machine n Design a TM which accept the language L(M)={0 n 1 n|n>=1} Initially it is given a finite sequence of 0’s and 1’s on its tape, preceded and followed by an infinity of blanks. The TM will change a 0 to an x and then 1 to a Y until all 0’s and 1’s have been matched. The formal specification of the TM is – M=({q 0, q 1, q 2, q 3, q 4}, {0, 1, X, Y, B}, ∂, q 0, B, {q 4})

Transition table for L(M)={0 n 1 n|n>=1} State 0 1 X Y B q

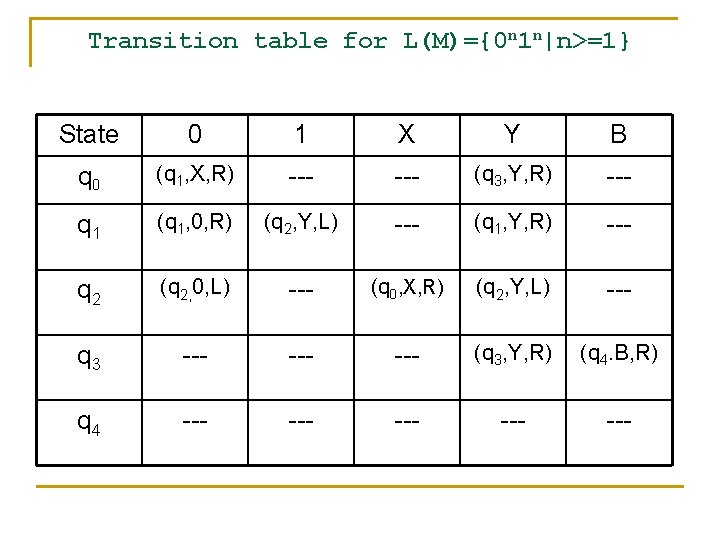
Transition table for L(M)={0 n 1 n|n>=1} State 0 1 X Y B q 0 (q 1, X, R) --- (q 3, Y, R) --- q 1 (q 1, 0, R) (q 2, Y, L) --- (q 1, Y, R) --- q 2 (q 2, 0, L) --- (q 0, X, R) (q 2, Y, L) --- q 3 --- --- (q 3, Y, R) (q 4. B, R) q 4 --- --- ---

Transition Diagram for L(M)={0 n 1 n|n>=1} Y/Y 0/0 0/X Start q 0 1/Y

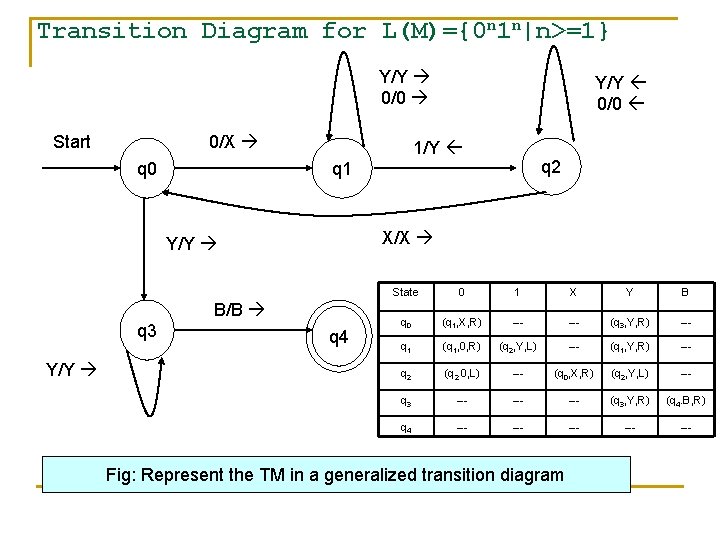
Transition Diagram for L(M)={0 n 1 n|n>=1} Y/Y 0/0 0/X Start q 0 1/Y X/X B/B Y/Y q 2 q 1 Y/Y q 3 Y/Y 0/0 q 4 State 0 1 X Y B q 0 (q 1, X, R) --- (q 3, Y, R) --- q 1 (q 1, 0, R) (q 2, Y, L) --- (q 1, Y, R) --- q 2 (q 2, 0, L) --- (q 0, X, R) (q 2, Y, L) --- q 3 --- --- (q 3, Y, R) (q 4. B, R) q 4 --- --- --- Fig: Represent the TM in a generalized transition diagram

Instantaneous Description of PDA n 1. 2. 3. The string X 1 X 2.

Instantaneous Description of PDA n 1. 2. 3. The string X 1 X 2. . Xi-1 q Xi Xi+1. . Xn is used to represent an ID in whichq is the state of a TM The tape head is scanning the ith symbol from the left. X 1 X 2. . . Xn is the portion of the tape between the leftmost and rightmost nonblank. Suppose ∂(q, Xi)=(p, Y, L), the next move is leftward, then X 1 X 2. . . Xi-1 q. Xi+1. . . Xn |- X 1 X 2. . . Xi-2 p. Xi-1 YXi. . . Xn More details follow book. . execeptions

Instantaneous Description of PDA n Here is an example of an accepting computation by

Instantaneous Description of PDA n Here is an example of an accepting computation by M, It’s input is 0011. Initially M is in state q 0, scanning the first 0, M’s initial ID is q 00011. The entire sequence of moves of M is: q 00011|-Xq 1011|-X 0 q 111|-Xq 20 Y 1|-q 2 X 0 Y 1|Xq 00 Y 1|-XXq 1 Y 1|- XXYq 11|- XXq 1 YY|- Xq 2 XYY|XXq 0 YY |- XXYq 3 Y|- XXYYq 3 B|-XXYYBq 4 B (accepted) State 0 1 X Y B q 0 (q 1, X, R) --- (q 3, Y, R) --- q 1 (q 1, 0, R) (q 2, Y, L) --- (q 1, Y, R) --- q 2 (q 2, 0, L) --- (q 0, X, R) (q 2, Y, L) --- q 3 --- --- (q 3, Y, R) (q 4. B, R) q 4 --- --- ---

Self Study for Exam n n Example-8. 4 Design a TM that compute the

Self Study for Exam n n Example-8. 4 Design a TM that compute the function (Proper Subtraction) Fig 8. 11, 8. 12 self

The Language of a TM n n Let M=(Q, ∑, Γ, ∂, q 0,

The Language of a TM n n Let M=(Q, ∑, Γ, ∂, q 0, B, F)be a TM, The L(M) is the set of strings w in ∑* Such that q 0 w|-αpβ for some state p in F and tape strings α and β The set of languages that are accepted using TM RE language (Recursively Enumerable). 8. 2. 6 TM and Halting A TM halts if it enters a state q scanning a tape symbol X, and there is no more on this situation is defined. Exercise 8. 2. 1, 8. 2. 2, 8. 2. 5 self (Important)