Chapter 6 Transportation Assignment and Transshipment Problems A

Chapter 6: Transportation, Assignment, and Transshipment Problems A network model is one which can be represented by a set of nodes, a set of arcs, and functions (e. g. costs, supplies, demands, etc. ) associated with the arcs and/or nodes. Examples include transportation, assignment, transshipment as well as shortest-route, maximal flow problems, minimal spanning tree and PERT/CPM problems. All network problems can be formulated as linear programs. However, there are many computer packages that contain separate computer codes for these problems which take advantage of their network structure. If the right-hand side of the linear programming formulations are all integers, then optimal solution of the decision variables will also be integers. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 1

Transportation Problem The transportation problem seeks to minimize the total shipping costs of transporting goods from m origins (each with a supply si) to n destinations (each with a demand dj), when the unit shipping cost from an origin, i, to a destination, j, is cij. The network representation for a transportation problem with two sources and three destinations is given on the next slide. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 2
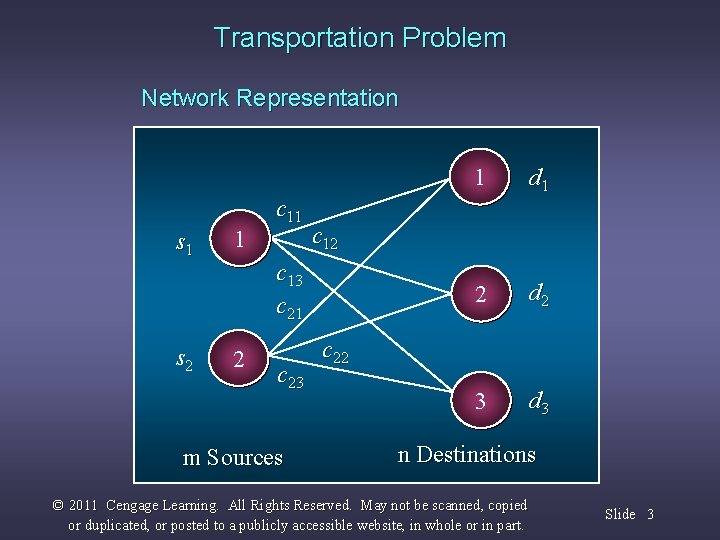
Transportation Problem Network Representation s 1 s 2 1 c 11 c 23 m Sources d 1 2 d 2 3 d 3 c 12 c 13 c 21 2 1 c 22 n Destinations © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 3

Transportation Problem Linear Programming Formulation Using the notation: xij = number of units shipped from origin i to destination j cij = cost per unit of shipping from origin i to destination j si = supply or capacity in units at origin i dj = demand in units at destination j continued © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 4

Transportation Problem Linear Programming Formulation (continued) xij > 0 for all i and j © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 5

Example: Transportation Problem The Navy has depots in Albany, Ben. Salem, and Winchester. Each of these three depots has 3, 000 pounds of materials which the Navy wishes to ship to three installations, namely, San Diego, Norfolk, and Pensacola. These installations require 4, 000, 2, 500, and 2, 500 pounds, respectively. The shipping costs per pound for are shown on the next slide. Formulate and solve a linear program to determine the shipping arrangements that will minimize the total shipping cost. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 6
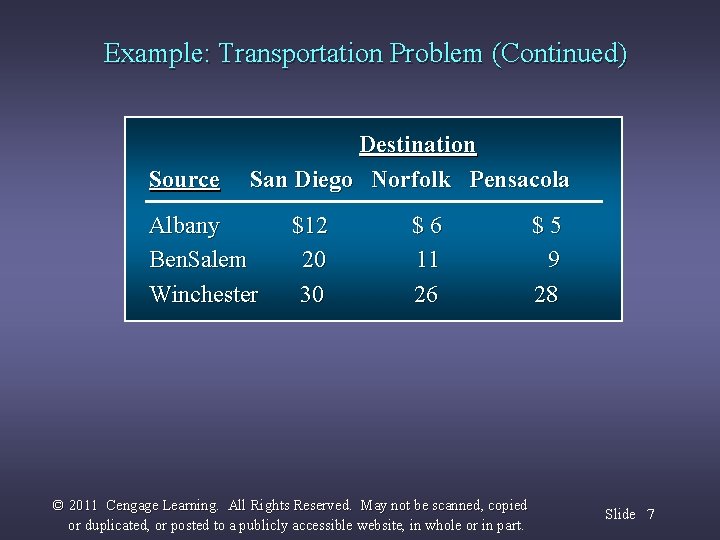
Example: Transportation Problem (Continued) Source Destination San Diego Norfolk Pensacola Albany Ben. Salem Winchester $12 20 30 $6 11 26 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. $5 9 28 Slide 7
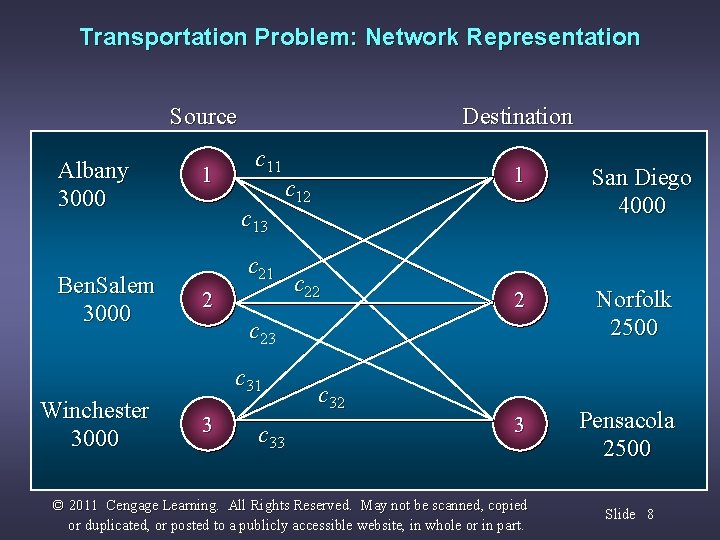
Transportation Problem: Network Representation Source Albany 3000 Ben. Salem 3000 1 Destination c 11 c 13 c 12 c 21 2 San Diego 4000 2 Norfolk 2500 3 Pensacola 2500 c 23 c 31 Winchester 3000 c 22 1 3 c 32 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 8

Example: Transportation Problem (Continued) Define the Decision Variables We want to determine the pounds of material, xij , to be shipped by mode i to destination j. The following table summarizes the decision variables: Albany Ben. Salem Winchester San Diego Norfolk Pensacola x 11 x 12 x 13 x 21 x 22 x 23 x 31 x 32 x 33 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 9

Example: Transportation Problem (Continued) Define the Objective Function Minimize the total shipping cost. Min: (shipping cost per pound for each mode per destination pairing) x (number of pounds shipped by mode per destination pairing). Min: 12 x 11 + 6 x 12 + 5 x 13 + 20 x 21 + 11 x 22 + 9 x 23 + 30 x 31 + 26 x 32 + 28 x 33 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 10

Transportation Problem: Example #2 Define the Constraints Source availability: (1) x 11 + x 12 + x 13 = 3000 (2) x 21 + x 22 + x 23 = 3000 (3) x 31 + x 32 + x 33 = 3000 Destination material requirements: (4) x 11 + x 21 + x 31 = 4000 (5) x 12 + x 22 + x 32 = 2500 (6) x 13 + x 23 + x 33 = 2500 Non-negativity of variables: xij > 0, i = 1, 2, 3 and j = 1, 2, 3 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 11

Example: Transportation Problem (Continued) Computer Output OBJECTIVE FUNCTION VALUE = 142000. 000 Variable Value Reduced Cost x 11 1000. 000 x 12 2000. 000 x 13 0. 000 1. 000 x 21 0. 000 3. 000 x 22 500. 000 x 23 2500. 000 x 31 3000. 000 x 32 0. 000 2. 000 x 33 0. 000 6. 000 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 12

Transportation Problem: Example #2 Solution Summary • San Diego will receive 1000 lbs. from Albany and 3000 lbs. from Winchester. • Norfolk will receive 2000 lbs. from Albany and 500 lbs. from Ben. Salem. • Pensacola will receive 2500 lbs. from Ben. Salem. • The total shipping cost will be $142, 000. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 13

Transportation Problem LP Formulation Special Cases • Total supply exceeds total demand: No modification of LP formulation is necessary. • Total demand exceeds total supply: Add a dummy origin with supply equal to the shortage amount. Assign a zero shipping cost per unit. The amount “shipped” from the dummy origin (in the solution) will not actually be shipped. Assign a zero shipping cost per unit • Maximum route capacity from i to j: © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 14

Transportation Problem LP Formulation Special Cases (continued) • The objective is maximizing profit or revenue: Solve as a maximization problem. • Minimum shipping guarantee from i to j: xij > Lij • Maximum route capacity from i to j: xij < Lij • Unacceptable route: Remove the corresponding decision variable. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 15

Assignment Problem An assignment problem seeks to minimize the total cost assignment of m workers to m jobs, given that the cost of worker i performing job j is cij. It assumes all workers are assigned and each job is performed. An assignment problem is a special case of a transportation problem in which all supplies and all demands are equal to 1; hence assignment problems may be solved as linear programs. The network representation of an assignment problem with three workers and three jobs is shown on the next slide. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 16
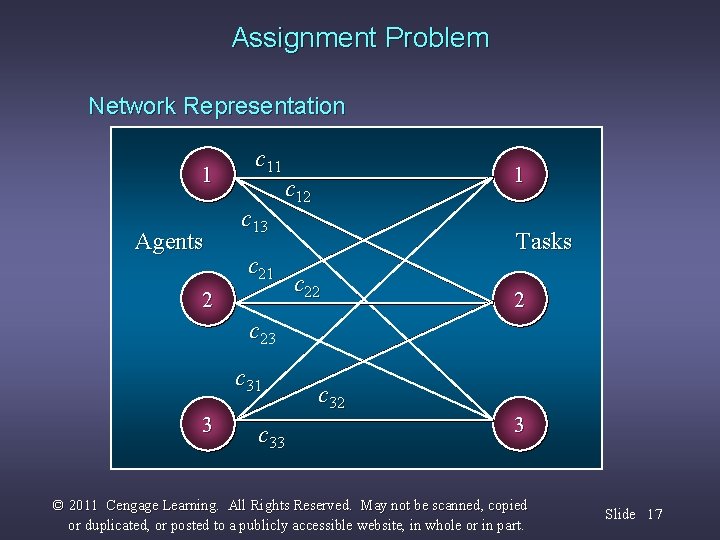
Assignment Problem Network Representation 1 Agents c 11 c 13 1 c 12 c 21 2 Tasks c 22 2 c 23 c 31 3 c 32 3 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 17

Assignment Problem Linear Programming Formulation Using the notation: xij = 1 if agent i is assigned to task j 0 otherwise cij = cost of assigning agent i to task j continued © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 18

Assignment Problem Linear Programming Formulation (continued) xij > 0 for all i and j © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 19

Example: Assignment Problem An electrical contractor pays his subcontractors a fixed fee plus mileage for work performed. On a given day the contractor is faced with three electrical jobs associated with various projects. Given below are the distances between the subcontractors and the projects. Projects Subcontractor A B C Westside 50 36 16 Federated 28 30 18 Goliath 35 32 20 Universal 25 25 14 How should the contractors be assigned so that total mileage is minimized? © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 20
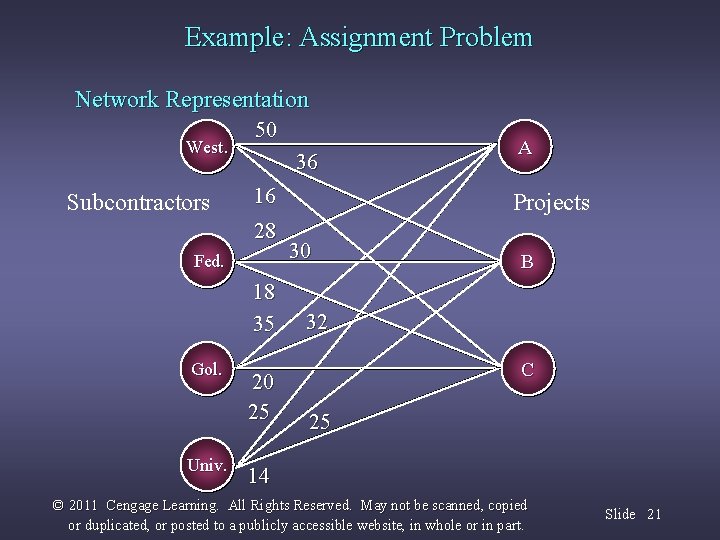
Example: Assignment Problem Network Representation West. Subcontractors 50 36 16 28 Fed. 18 35 Gol. Univ. 20 25 A Projects 30 B 32 C 25 14 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 21

Assignment Problem: Example Linear Programming Formulation Min 50 x 11+36 x 12+16 x 13+28 x 21+30 x 22+18 x 23 +35 x 31+32 x 32+20 x 33+25 x 41+25 x 42+14 x 43 s. t. x 11+x 12+x 13 < 1 x 21+x 22+x 23 < 1 Agents x 31+x 32+x 33 < 1 x 41+x 42+x 43 < 1 x 11+x 21+x 31+x 41 = 1 x 12+x 22+x 32+x 42 = 1 Tasks x 13+x 23+x 33+x 43 = 1 xij = 0 or 1 for all i and j © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 22

Assignment Problem: Example The optimal assignment is: Subcontractor Project Distance Westside C 16 Federated A 28 Goliath (unassigned) Universal B 25 Total Distance = 69 miles © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 23

Assignment Problem LP Formulation Special Cases • Number of agents exceeds the number of tasks: Extra agents simply remain unassigned. • Number of tasks exceeds the number of agents: Add enough dummy agents to equalize the number of agents and the number of tasks. The objective function coefficients for these new variable would be zero. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 24

Assignment Problem LP Formulation Special Cases (continued) • The assignment alternatives are evaluated in terms of revenue or profit: Solve as a maximization problem. • An assignment is unacceptable: Remove the corresponding decision variable. • An agent is permitted to work t tasks: © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 25

Transshipment Problem Transshipment problems are transportation problems in which a shipment may move through intermediate nodes (transshipment nodes)before reaching a particular destination node. Transshipment problems can be converted to larger transportation problems and solved by a special transportation program. Transshipment problems can also be solved by general purpose linear programming codes. The network representation for a transshipment problem with two sources, three intermediate nodes, and two destinations is shown on the next slide. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 26
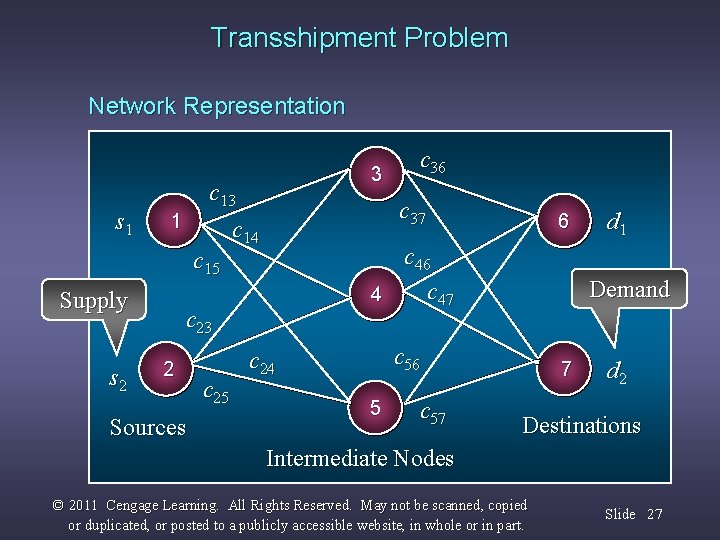
Transshipment Problem Network Representation s 1 c 13 1 c 15 Supply s 2 3 c 37 c 14 Sources c 25 6 c 47 4 c 23 2 c 36 Demand c 56 c 24 5 c 57 d 1 7 d 2 Destinations Intermediate Nodes © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 27

Transshipment Problem Linear Programming Formulation Using the notation: xij = number of units shipped from node i to node j cij = cost per unit of shipping from node i to node j si = supply at origin node i dj = demand at destination node j continued © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 28

Transshipment Problem Linear Programming Formulation (continued) xij > 0 for all i and j continued © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 29

Transshipment Problem LP Formulation Special Cases • Total supply not equal to total demand • Maximization objective function • Route capacities or route minimums • Unacceptable routes The LP model modifications required here are identical to those required for the special cases in the transportation problem. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 30

Transshipment Problem Example The Northside and Southside facilities of Zeron Industries supply three firms (Zrox, Hewes, Rockrite) with customized shelving for its offices. They both order shelving from the same two manufacturers, Arnold Manufacturers and Supershelf, Inc. Currently weekly demands by the users are 50 for Zrox, 60 for Hewes, and 40 for Rockrite. Both Arnold and Supershelf can supply at most 75 units to its customers. Additional data is shown on the next slide. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 31

Transshipment Problem Example Because of long standing contracts based on past orders, unit costs from the manufacturers to the suppliers are: Zeron N Zeron S Arnold 5 8 Supershelf 7 4 The costs to install the shelving at the various locations are: Zrox Hewes Rockrite Thomas 1 5 8 Washburn 3 4 4 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 32
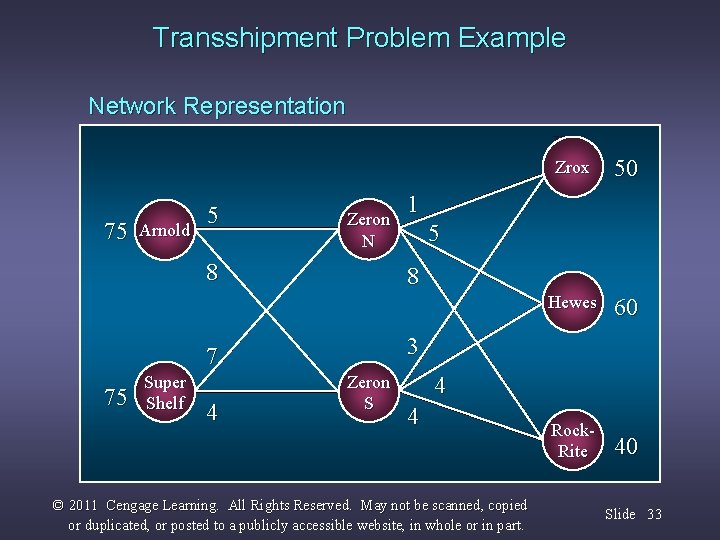
Transshipment Problem Example Network Representation ZROX 75 ARNOLD Arnold 5 Zeron N 8 75 Hewes HEWES 60 Rock. Rite 40 1 5 3 Zeron 4 50 8 7 Super Shelf Zrox Zeron WASH BURN S 4 4 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 33

Transshipment Problem: Example Linear Programming Formulation • Decision Variables Defined xij = amount shipped from manufacturer i to supplier j xjk = amount shipped from supplier j to customer k where i = 1 (Arnold), 2 (Supershelf) j = 3 (Zeron N), 4 (Zeron S) k = 5 (Zrox), 6 (Hewes), 7 (Rockrite) • Objective Function Defined Minimize Overall Shipping Costs: Min 5 x 13 + 8 x 14 + 7 x 23 + 4 x 24 + 1 x 35 + 5 x 36 + 8 x 37 + 3 x 45 + 4 x 46 + 4 x 47 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 34

Transshipment Problem: Example Constraints Defined Amount Out of Arnold: Amount Out of Supershelf: Amount Through Zeron N: 0 Amount Through Zeron S: 0 Amount Into Zrox: Amount Into Hewes: Amount Into Rockrite: x 13 + x 14 < 75 x 23 + x 24 < 75 x 13 + x 23 - x 35 - x 36 - x 37 = x 14 + x 24 - x 45 - x 46 - x 47 = x 35 + x 45 x 36 + x 46 x 37 + x 47 = = = 50 60 40 Non-negativity of Variables: xij > 0, for all i and j. © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 35
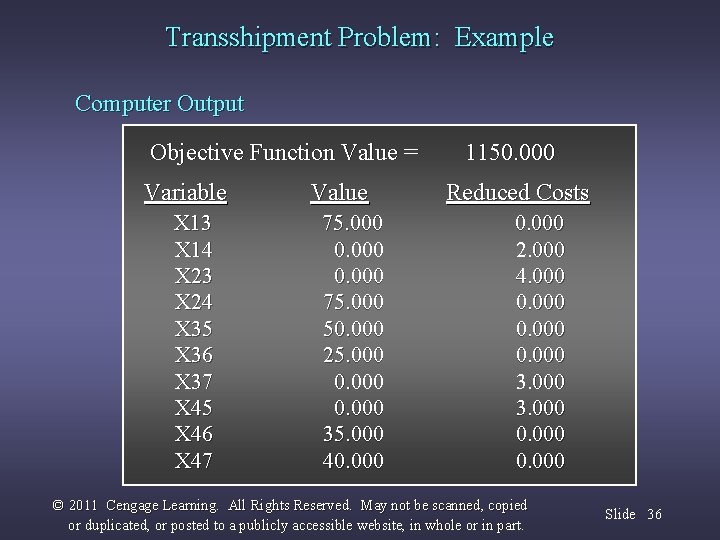
Transshipment Problem: Example Computer Output Objective Function Value = Variable X 13 X 14 X 23 X 24 X 35 X 36 X 37 X 45 X 46 X 47 Value 75. 000 0. 000 75. 000 50. 000 25. 000 0. 000 35. 000 40. 000 1150. 000 Reduced Costs 0. 000 2. 000 4. 000 0. 000 3. 000 0. 000 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 36
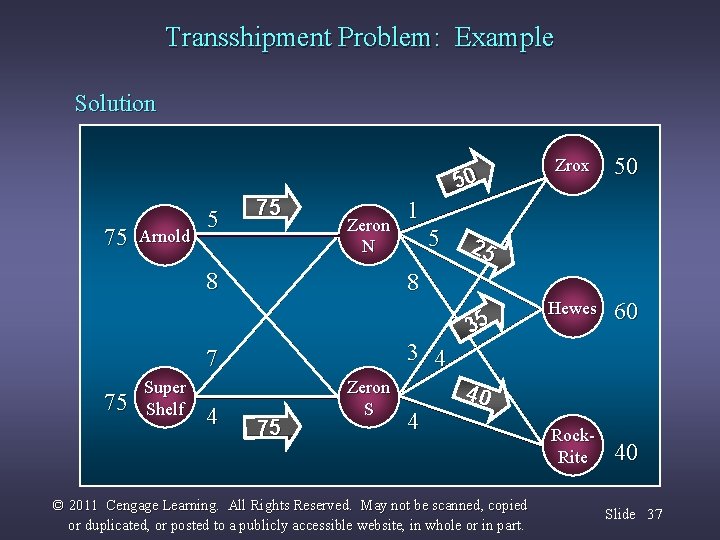
Transshipment Problem: Example Solution ZROX 50 75 ARNOLD Arnold 5 75 Zeron N 8 75 Hewes HEWES 60 Rock. Rite 40 1 5 3 4 Zeron 4 50 25 8 7 Super Shelf Zrox 75 Zeron WASH BURN S 4 35 40 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 37

Transshipment Problem: Example Computer Output (continued) Constraint 1 2 3 4 5 6 7 Slack/Surplus 0. 000 0. 000 Dual Values 0. 000 2. 000 -5. 000 -6. 000 -10. 000 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 38
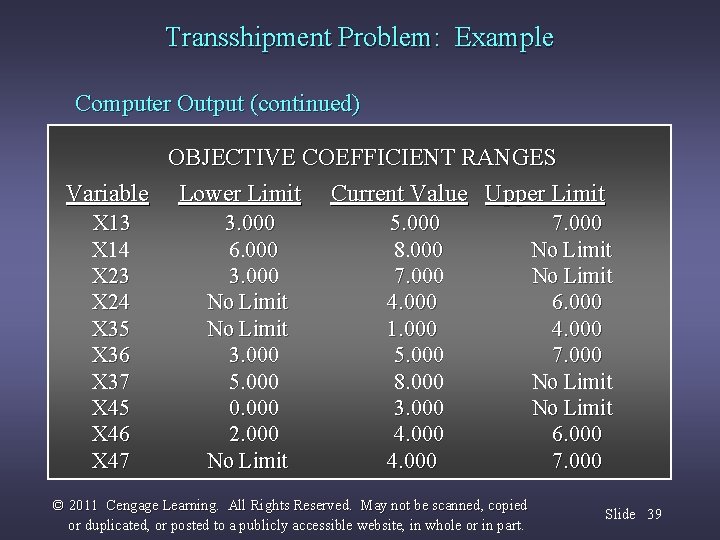
Transshipment Problem: Example Computer Output (continued) OBJECTIVE COEFFICIENT RANGES Variable Lower Limit Current Value Upper Limit X 13 X 14 X 23 X 24 X 35 X 36 X 37 X 45 X 46 X 47 3. 000 6. 000 3. 000 No Limit 3. 000 5. 000 0. 000 2. 000 No Limit 5. 000 8. 000 7. 000 4. 000 1. 000 5. 000 8. 000 3. 000 4. 000 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 7. 000 No Limit 6. 000 4. 000 7. 000 No Limit 6. 000 7. 000 Slide 39
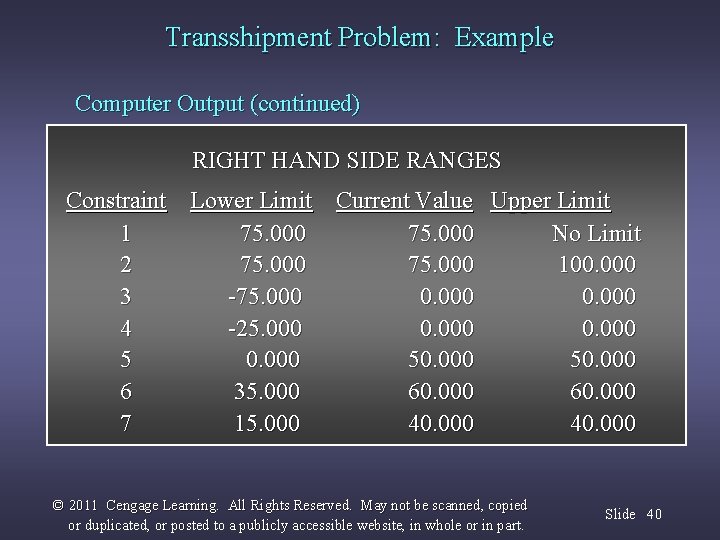
Transshipment Problem: Example Computer Output (continued) RIGHT HAND SIDE RANGES Constraint Lower Limit Current Value Upper Limit 1 75. 000 No Limit 2 75. 000 100. 000 3 -75. 000 0. 000 4 -25. 000 0. 000 50. 000 6 35. 000 60. 000 7 15. 000 40. 000 © 2011 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Slide 40
- Slides: 40