Chapter 6 The Normal Distribution and Other Continuous

Chapter 6 The Normal Distribution and Other Continuous Distributions Yandell – Econ 216 Chap 6 -1

Chapter Goals After completing this chapter, you should be able to: n n n Describe the characteristics of the normal distribution Translate normal distribution problems into standard normal distribution problems Find probabilities using a normal distribution table and apply the normal distribution to business situations Use PHStat to obtain normal probabilities Recognize when to apply the uniform and exponential distributions Yandell – Econ 216 Chap 6 -2

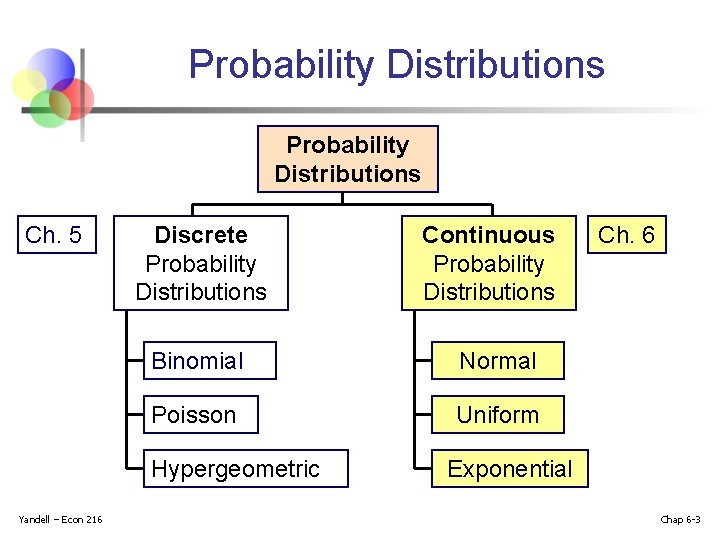
Probability Distributions Ch. 5 Discrete Probability Distributions Binomial Normal Poisson Uniform Hypergeometric Yandell – Econ 216 Continuous Probability Distributions Ch. 6 Exponential Chap 6 -3

Continuous Probability Distributions n A continuous random variable is a variable that can assume any value on a continuum (can assume an uncountable number of values) n n n Yandell – Econ 216 thickness of an item time required to complete a task temperature of a solution height, in inches These can potentially take on any value, depending only on the ability to measure accurately. Chap 6 -4

The Normal Distribution Probability Distributions Continuous Probability Distributions Normal Uniform Exponential Yandell – Econ 216 Chap 6 -5

The Normal Distribution ‘Bell Shaped’ n Symmetrical n Mean, Median and Mode are Equal Location is determined by the mean, μ n Spread is determined by the standard deviation, σ The random variable has an infinite theoretical range: + to Yandell – Econ 216 f(X) σ X μ Mean = Median = Mode Chap 6 -6

Many Normal Distributions listen By varying the parameters μ and σ, we obtain different normal distributions Yandell – Econ 216 Chap 6 -7

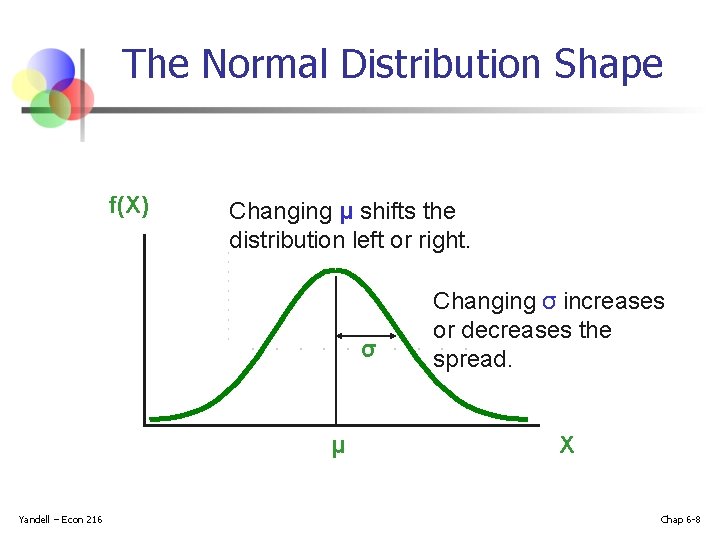
The Normal Distribution Shape f(X) Changing μ shifts the distribution left or right. σ μ Yandell – Econ 216 Changing σ increases or decreases the spread. X Chap 6 -8

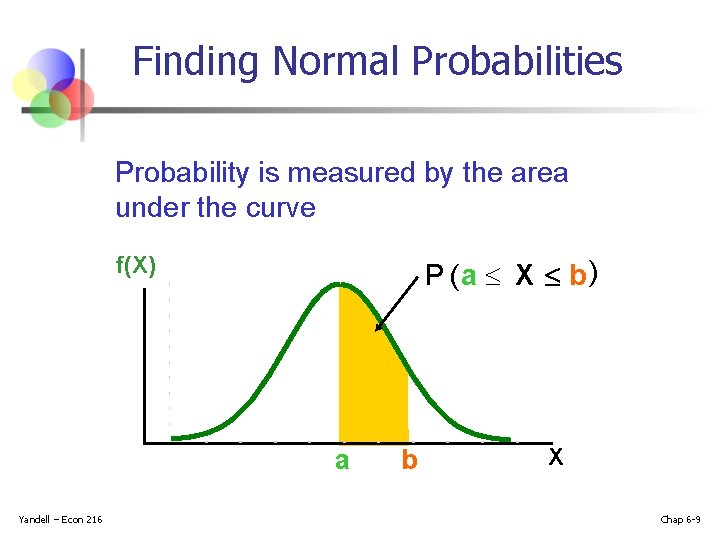
Finding Normal Probabilities Probability is the Probability is measured area under the curve! under the curve f(X) P (a X b) a Yandell – Econ 216 by the area b X Chap 6 -9

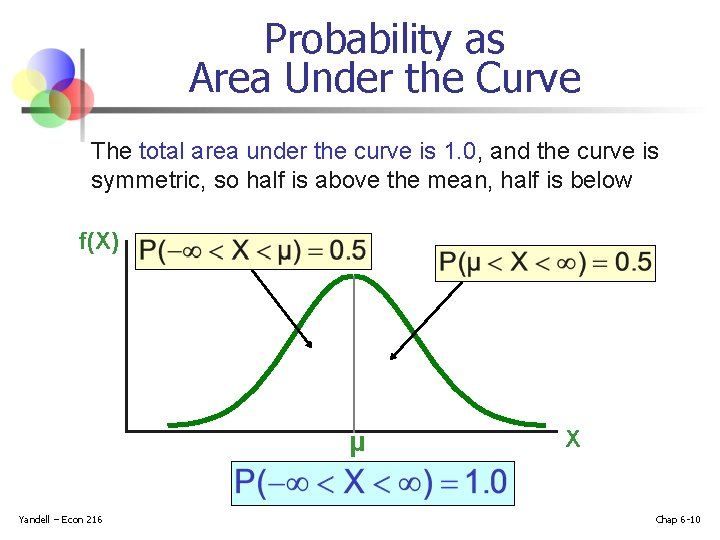
Probability as Area Under the Curve The total area under the curve is 1. 0, and the curve is symmetric, so half is above the mean, half is below f(X) 0. 5 μ Yandell – Econ 216 X Chap 6 -10

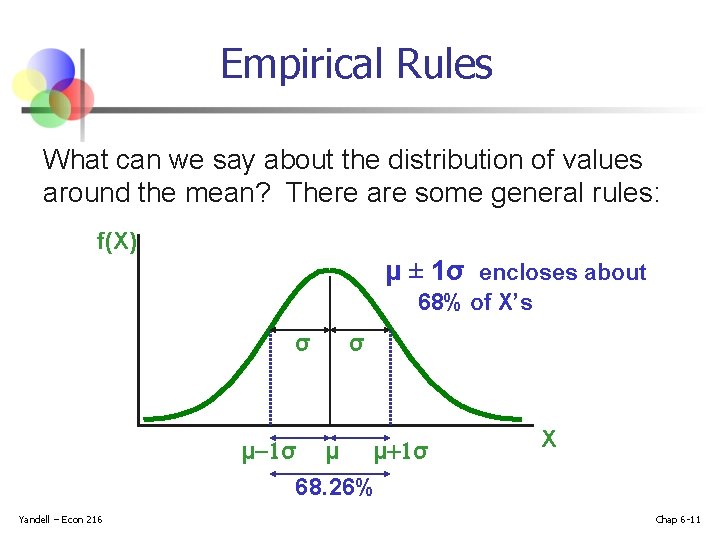
Empirical Rules What can we say about the distribution of values around the mean? There are some general rules: f(X) μ ± 1σ encloses about 68% of X’s σ μ 1σ σ μ μ+1σ X 68. 26% Yandell – Econ 216 Chap 6 -11

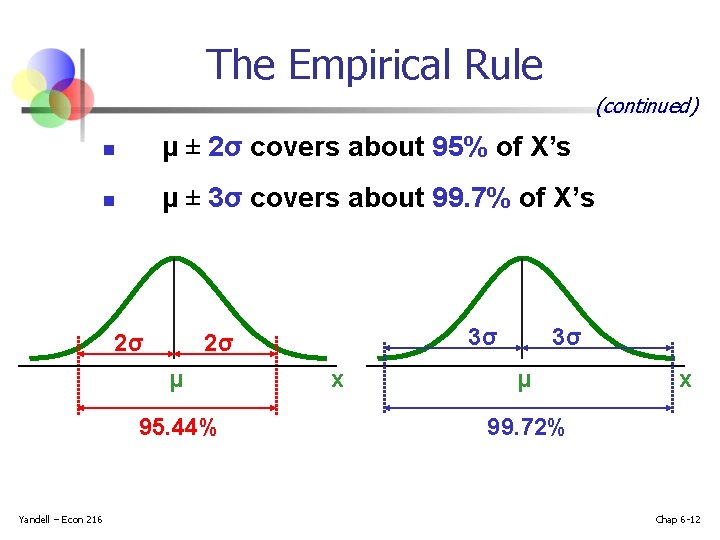
The Empirical Rule (continued) n μ ± 2σ covers about 95% of X’s n μ ± 3σ covers about 99. 7% of X’s 2σ μ 95. 44% Yandell – Econ 216 3σ 2σ x 3σ μ x 99. 72% Chap 6 -12

Importance of the Rule n n If a value is about 2 or more standard deviations away from the mean in a normal distribution, then it is far from the mean The chance that a value that far or farther away from the mean is highly unlikely, given that particular mean and standard deviation Yandell – Econ 216 Chap 6 -13

Inference n n Yandell – Econ 216 Put another way, when a value of X is observed that is far from a hypothesized value for the mean, because this observation is so unlikely if the hypothesis is true, it casts strong doubt on the claim about the mean. (More in Chapters 7 and 8) Chap 6 -14

The Standard Normal Distribution n Also known as the “Z” distribution Mean is defined to be 0 Standard Deviation is 1 f(Z) 1 0 Z Values above the mean have positive Z-values, values below the mean have negative Z-values Yandell – Econ 216 Chap 6 -15

The Standard Normal n n Yandell – Econ 216 Any normal distribution (with any mean and standard deviation combination) can be transformed into the standard normal distribution (Z) Need to transform X units into Z units Chap 6 -16

Translation to the Standard Normal Distribution n Yandell – Econ 216 Translate from X to the standard normal (the “Z” distribution) by subtracting the mean of X and dividing by its standard deviation: Chap 6 -17

Example n n If X is distributed normally with mean of 100 and standard deviation of 50, the Z value for X = 200 is This says that X = 200 is two standard deviations (2 increments of 50 units) above the mean of 100. Yandell – Econ 216 Chap 6 -18

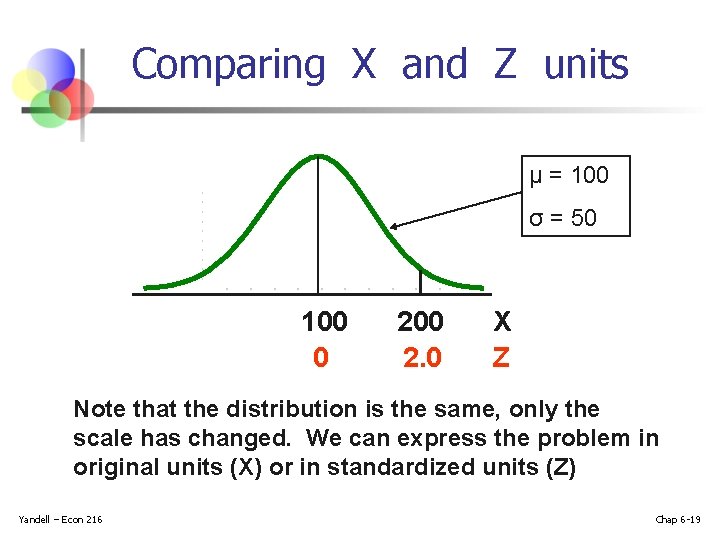
Comparing X and Z units μ = 100 σ = 50 100 0 200 2. 0 X Z Note that the distribution is the same, only the scale has changed. We can express the problem in original units (X) or in standardized units (Z) Yandell – Econ 216 Chap 6 -19

The Standard Normal Table n The Standard Normal table in the textbook (Appendix table E. 2) gives the probability less than a desired value for Z (i. e. , from negative infinity to Z). 9772 Example: P(Z < 2. 00) =. 9772 0 Yandell – Econ 216 2. 00 Z Chap 6 -20

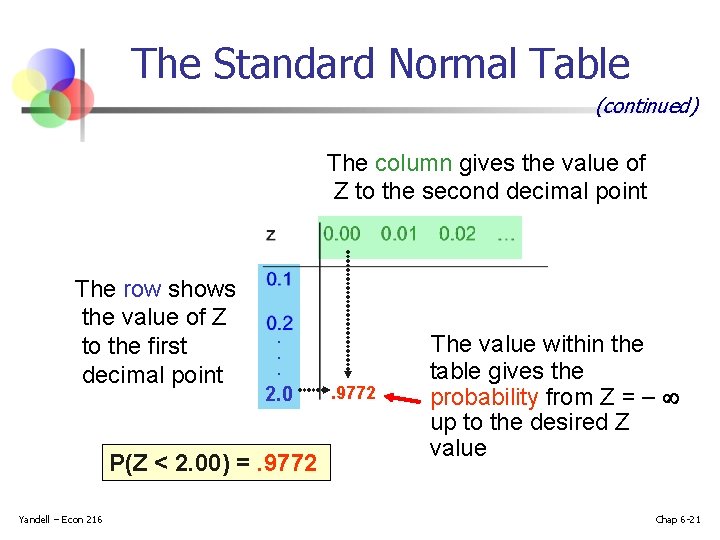
The Standard Normal Table (continued) The column gives the value of Z to the second decimal point The row shows the value of Z to the first decimal point . . . 2. 0 P(Z < 2. 00) =. 9772 Yandell – Econ 216 . 9772 The value within the table gives the probability from Z = up to the desired Z value Chap 6 -21

General Procedure for Finding Probabilities To find P(a < X < b) when X is distributed normally: n Draw the normal curve for the problem in terms of X n Translate X-values to Z-values n Use the Standard Normal Table Yandell – Econ 216 Chap 6 -22

Finding Normal Probabilities Suppose X is normal with mean 8. 0 and standard deviation 5. 0 n Find P(X < 8. 6) n X 8. 0 8. 6 Yandell – Econ 216 Chap 6 -23

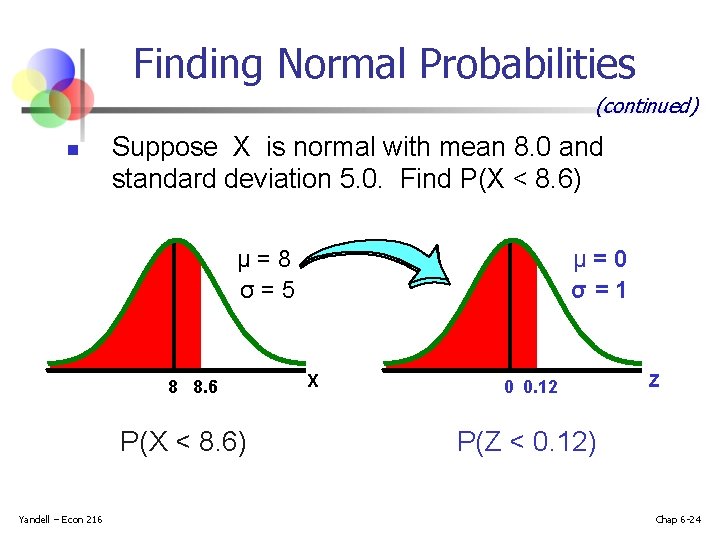
Finding Normal Probabilities (continued) n Suppose X is normal with mean 8. 0 and standard deviation 5. 0. Find P(X < 8. 6) μ=8 σ=5 8 8. 6 P(X < 8. 6) Yandell – Econ 216 μ=0 σ=1 X 0 0. 12 Z P(Z < 0. 12) Chap 6 -24

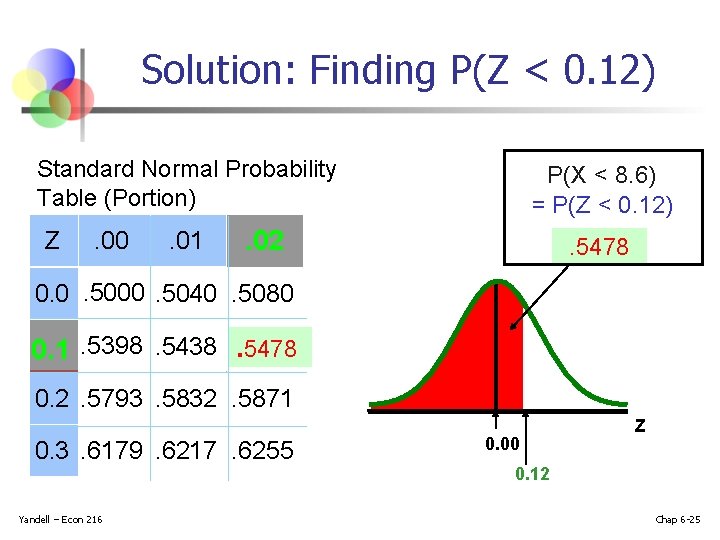
Solution: Finding P(Z < 0. 12) Standard Normal Probability Table (Portion) Z . 00 . 01 P(X < 8. 6) = P(Z < 0. 12) . 02 . 5478 0. 0. 5000. 5040. 5080 0. 1. 5398. 5438. 5478 0. 2. 5793. 5832. 5871 0. 3. 6179. 6217. 6255 Yandell – Econ 216 0. 00 Z 0. 12 Chap 6 -25

Upper Tail Probabilities Suppose X is normal with mean 8. 0 and standard deviation 5. 0. n Now Find P(X > 8. 6) n X 8. 0 8. 6 Yandell – Econ 216 Chap 6 -26

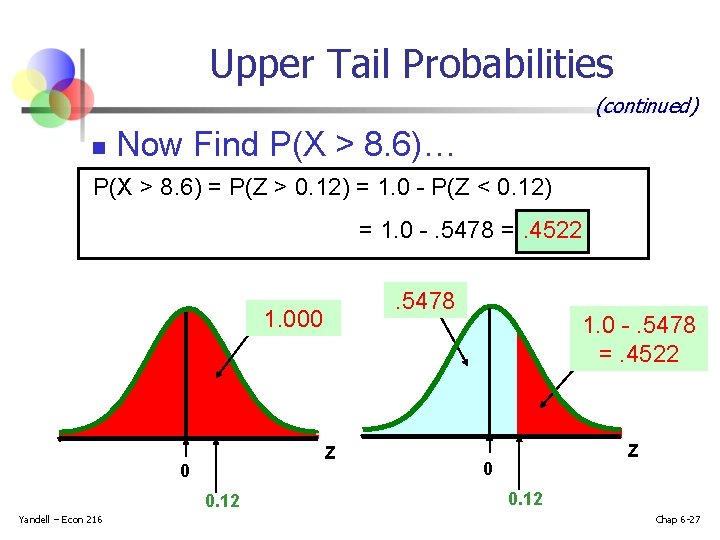
Upper Tail Probabilities (continued) n Now Find P(X > 8. 6)… P(X > 8. 6) = P(Z > 0. 12) = 1. 0 - P(Z < 0. 12) = 1. 0 -. 5478 =. 4522. 5478 1. 000 Z 0 0. 12 Yandell – Econ 216 1. 0 -. 5478 =. 4522 Z 0 0. 12 Chap 6 -27

Probability Between Two Values n Suppose X is normal with mean 8. 0 and standard deviation 5. 0. Find P(8 < X < 8. 6) Calculate Z-values: 8 8. 6 X 0 0. 12 Z P(8 < X < 8. 6) = P(0 < Z < 0. 12) Yandell – Econ 216 Chap 6 -28

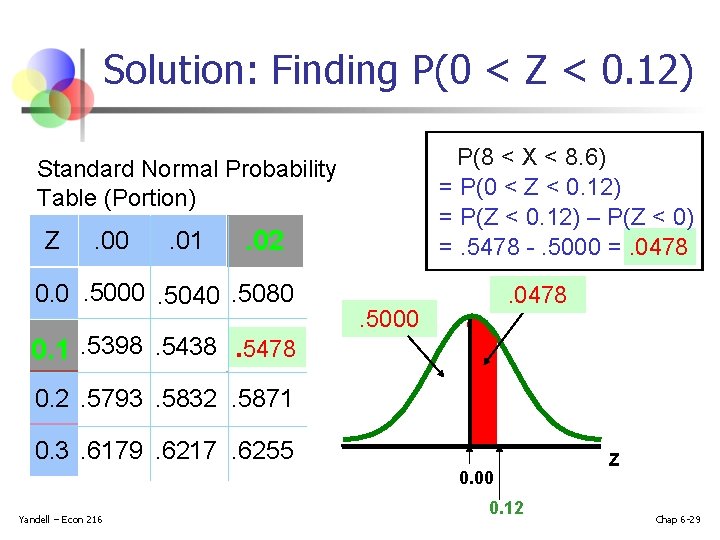
Solution: Finding P(0 < Z < 0. 12) P(8 < X < 8. 6) = P(0 < Z < 0. 12) = P(Z < 0. 12) – P(Z < 0) =. 5478 -. 5000 =. 0478 Standard Normal Probability Table (Portion) Z . 00 . 01 . 02 0. 0. 5000. 5040. 5080 0. 1. 5398. 5438. 5478 . 0478 . 5000 0. 2. 5793. 5832. 5871 0. 3. 6179. 6217. 6255 0. 00 Yandell – Econ 216 0. 12 Z Chap 6 -29

Lower Tail Probabilities Suppose X is normal with mean 8. 0 and standard deviation 5. 0. n Now Find P(7. 4 < X < 8) n 7. 4 Yandell – Econ 216 8. 0 X Chap 6 -30

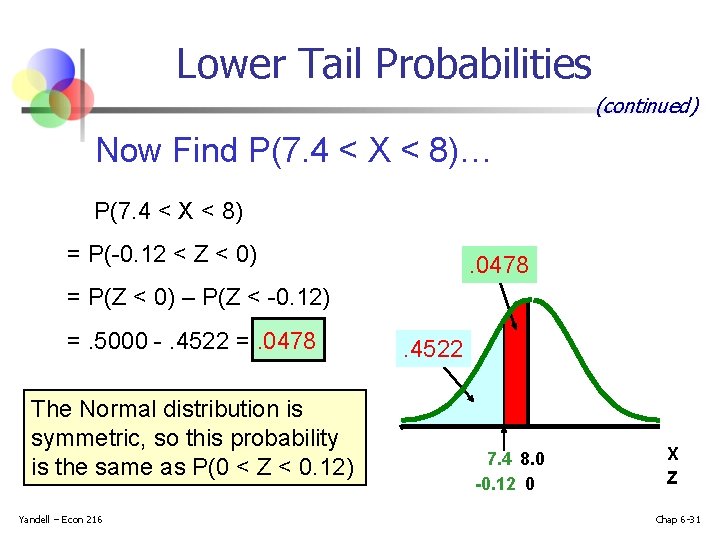
Lower Tail Probabilities (continued) Now Find P(7. 4 < X < 8)… P(7. 4 < X < 8) = P(-0. 12 < Z < 0) . 0478 = P(Z < 0) – P(Z < -0. 12) =. 5000 -. 4522 =. 0478 The Normal distribution is symmetric, so this probability is the same as P(0 < Z < 0. 12) Yandell – Econ 216 . 4522 7. 4 8. 0 -0. 12 0 X Z Chap 6 -31

Normal Probabilities in PHStat n n Yandell – Econ 216 We can use Excel and PHStat to quickly generate probabilities for any normal distribution We will find P(8 < X < 8. 6) when X is normally distributed with mean 8 and standard deviation 5 Chap 6 -32

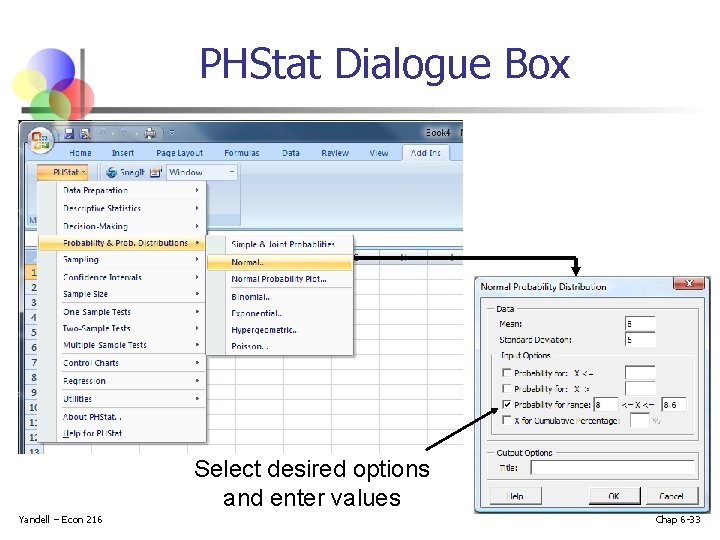
PHStat Dialogue Box Select desired options and enter values Yandell – Econ 216 Chap 6 -33

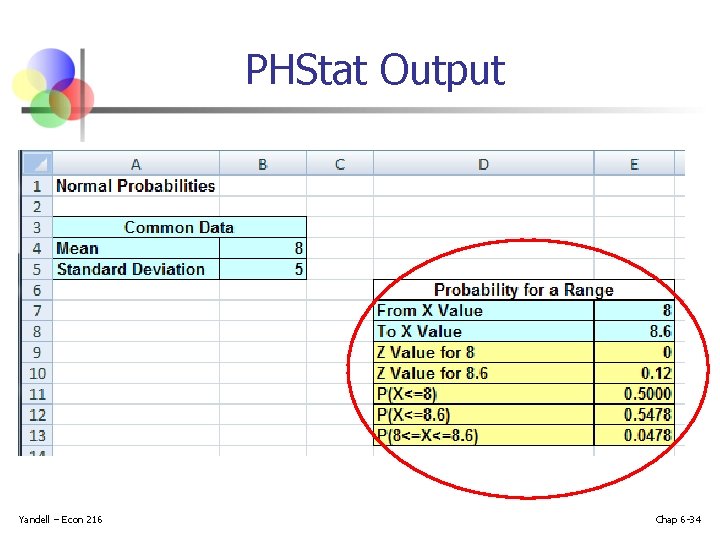
PHStat Output Yandell – Econ 216 Chap 6 -34

PHStat Demo n Click below to view a Ph. Stat demo to see how to get P(5 < X < 6. 2) , if μ = 5 and σ = 10: Click here to view normal distribution demo Yandell – Econ 216 Chap 6 -35

Upper Tail Practice Problem What value c from a standard normal distribution cuts off 5% in the upper tail? n i. e. , what is c so that P(Z > c) =. 05 ? n . 05 Z 0 C Yandell – Econ 216 Chap 6 -36

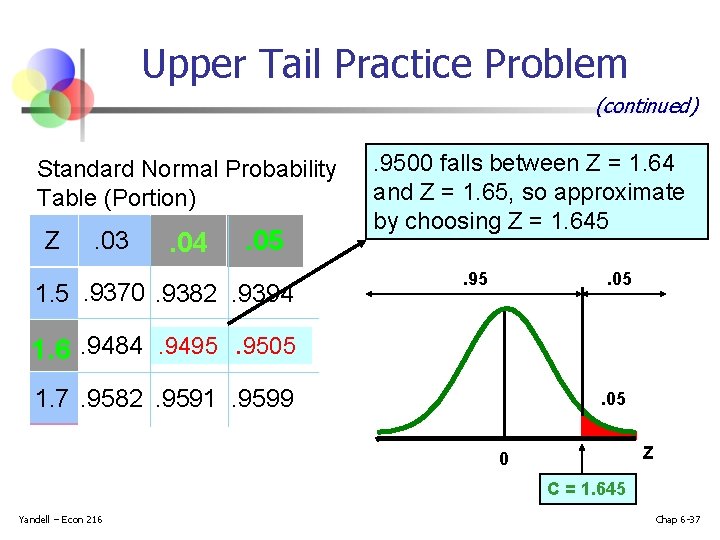
Upper Tail Practice Problem (continued) Standard Normal Probability Table (Portion) Z . 03 . 04 . 05 1. 5. 9370. 9382. 9394 . 9500 falls between Z = 1. 64 and Z = 1. 65, so approximate by choosing Z = 1. 645. 95 . 05 1. 6. 9484. 9495. 9505 1. 7. 9582. 9591. 9599 . 05 Z 0 C = 1. 645 Yandell – Econ 216 Chap 6 -37

Practice Problem Demo Click here to view the demonstration Click here to open the excel sheet to see the details (Z_table_upper 5 pct. xls) Yandell – Econ 216 Chap 6 -38

The Uniform Distribution Probability Distributions Continuous Probability Distributions Normal Uniform Exponential Yandell – Econ 216 Chap 6 -39

The Uniform Distribution n Yandell – Econ 216 The uniform distribution is a probability distribution that has equal probabilities for all possible outcomes of the random variable Chap 6 -40

The Uniform Distribution (continued) The Continuous Uniform Distribution: f(X) = where f(X) = value of the density function at any X value a = lower limit of the interval b = upper limit of the interval Yandell – Econ 216 Chap 6 -41

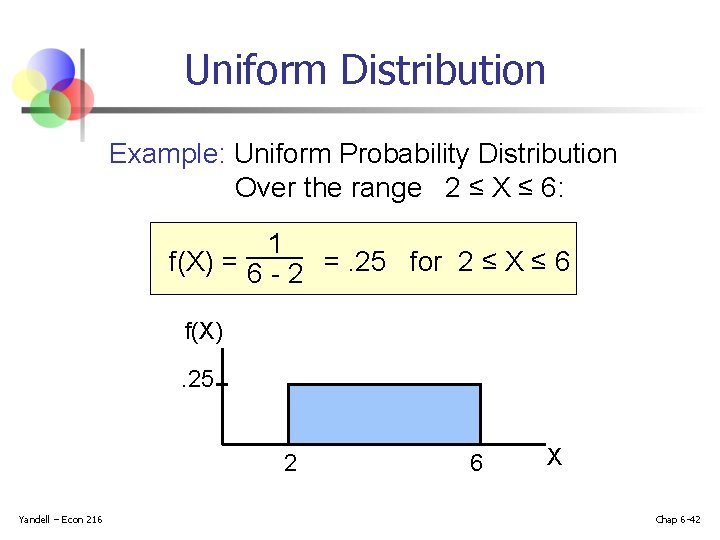
Uniform Distribution Example: Uniform Probability Distribution Over the range 2 ≤ X ≤ 6: 1 f(X) = 6 - 2 =. 25 for 2 ≤ X ≤ 6 f(X). 25 2 Yandell – Econ 216 6 X Chap 6 -42

The Exponential Distribution Probability Distributions Continuous Probability Distributions Normal Uniform Exponential Yandell – Econ 216 Chap 6 -43

The Exponential Distribution n Used to measure the time that elapses between two occurrences of an event (the time between arrivals) n Yandell – Econ 216 Examples: n Time between trucks arriving at an unloading dock n Time between transactions at an ATM Machine n Time between phone calls to the main operator Chap 6 -44

The Exponential Distribution n The probability that an arrival time is equal to or less than some specified time a is where 1/ is the mean time between events Note that if the number of occurrences per time period is Poisson with mean , then the time between occurrences is exponential with mean time 1/ Yandell – Econ 216 Chap 6 -45

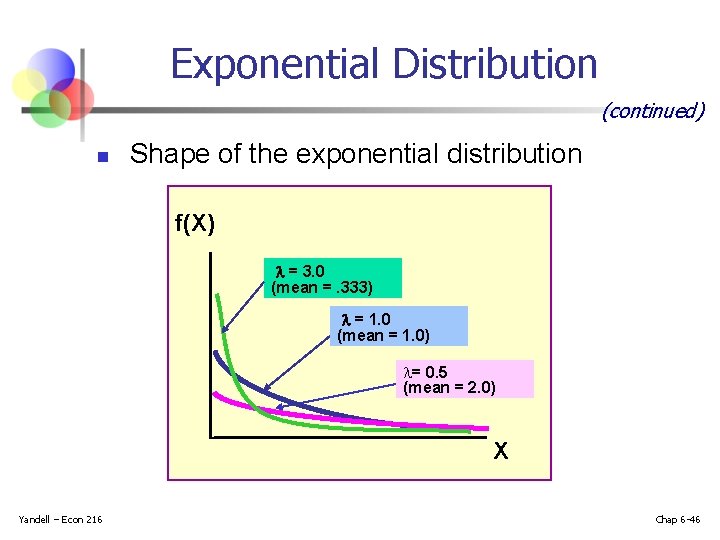
Exponential Distribution (continued) n Shape of the exponential distribution f(X) = 3. 0 (mean =. 333) = 1. 0 (mean = 1. 0) = 0. 5 (mean = 2. 0) X Yandell – Econ 216 Chap 6 -46

Example: Customers arrive at the claims counter at the rate of 15 per hour (Poisson distributed). What is the probability that the arrival time between consecutive customers is less than five minutes? Yandell – Econ 216 § Time between arrivals is exponentially distributed with mean time between arrivals of 4 minutes (15 per 60 minutes, on average) § 1/ = 4. 0, so =. 25 § P(x < 5) = 1 - e- a = 1 – e-(. 25)(5) =. 7135 Chap 6 -47

Chapter Summary n Introduced the Normal probability distribution n Found probabilities using formulas and tables n Discussed the Standard Normal Distribution and applied it to decision problems n Reviewed other continuous distributions n Yandell – Econ 216 uniform, exponential Chap 6 -48