Chapter 6 The Binomial Probability Distribution and Related

Chapter 6 The Binomial Probability Distribution and Related Topics Understanding Basic Statistics Fifth Edition By Brase and Brase Prepared by Jon Booze

Statistical Experiments and Random Variables • Statistical Experiments – any process by which measurements are obtained. • A quantitative variable, x, is a random variable if its value is determined by the outcome of a random experiment. • Random variables can be discrete or continuous. Copyright © Cengage Learning. All rights reserved. 6 | 2

Random Variables and Their Probability Distributions • Discrete random variables – can take on only a countable or finite number of values. • Continuous random variables – can take on countless values in an interval on the real line • Probability distributions of random variables – An assignment of probabilities to the specific values or a range of values for a random variable. Copyright © Cengage Learning. All rights reserved. 6 | 3

Random Variables and Their Probability Distributions Which measurement involves a discrete random variable? a). Determine the mass of a randomly-selected penny b). Assess customer satisfaction rated from 1 (completely satisfied) to 5 (completely dissatisfied). c). Find the rate of occurrence of a genetic disorder in a given sample of persons. d). Measure the percentage of light bulbs with lifetimes less than 400 hours. Copyright © Cengage Learning. All rights reserved. 6 | 4

Random Variables and Their Probability Distributions Which measurement involves a discrete random variable? a). Determine the mass of a randomly-selected penny b). Assess customer satisfaction rated from 1 (completely satisfied) to 5 (completely dissatisfied). c). Find the rate of occurrence of a genetic disorder in a given sample of persons. d). Measure the percentage of light bulbs with lifetimes less than 400 hours. Copyright © Cengage Learning. All rights reserved. 6 | 5

Discrete Probability Distributions 1) Each value of the random variable has an assigned probability. 2) The sum of all the assigned probabilities must equal 1. Copyright © Cengage Learning. All rights reserved. 6 | 6

Probability Distribution Features • Since a probability distribution can be thought of as a relative-frequency distribution for a very large n, we can find the mean and the standard deviation. • When viewing the distribution in terms of the population, use µ for the mean and σ for the standard deviation. Copyright © Cengage Learning. All rights reserved. 6 | 7

Means and Standard Deviations for Discrete Probability Distributions Copyright © Cengage Learning. All rights reserved. 6 | 8

Binomial Experiments 1) There a fixed number of trials. This is denoted by n. 2) The n trials are independent and repeated under identical conditions. 3) Each trial has two outcomes: S = success Copyright © Cengage Learning. All rights reserved. F = failure 6 | 9

Binomial Experiments Which of the following does not involve binomial trials? a). A recyclable item is placed into a bin meant for paper, plastic, or glass. b). A randomly-selected student passes a statistics course. c). A electronic power supply is rejected if it delivers less than 300 milliamps of current. d). A given concept is classified as “traditional” or “modern”. Copyright © Cengage Learning. All rights reserved. 6 | 10

Binomial Experiments Which of the following does not involve binomial trials? a). A recyclable item is placed into a bin meant for paper, plastic, or glass. b). A randomly-selected student passes a statistics course. c). A electronic power supply is rejected if it delivers less than 300 milliamps of current. d). A given concept is classified as “traditional” or “modern”. Copyright © Cengage Learning. All rights reserved. 6 | 11

Binomial Experiments 4) For each trial, the probability of success, p, remains the same. Thus, the probability of failure is 1 – p = q. 5) The central problem is to determine the probability of r successes out of n trials. Copyright © Cengage Learning. All rights reserved. 6 | 12

Determining Binomial Probabilities 1) Use the Binomial Probability Formula. 2) Use Table 2 of the appendix. 3) Use technology. Copyright © Cengage Learning. All rights reserved. 6 | 13

Binomial Probability Formula Copyright © Cengage Learning. All rights reserved. 6 | 14

Binomial Probability Formula Find the probability of observing 6 successes in 10 trials if the probability of success is p = 0. 4. a). 0. 111 b). 0. 251 Copyright © Cengage Learning. All rights reserved. c). 0. 0002 d). 0. 022 6 | 15

Binomial Probability Formula Find the probability of observing 6 successes in 10 trials if the probability of success is p = 0. 4. a). 0. 111 b). 0. 251 Copyright © Cengage Learning. All rights reserved. c). 0. 0002 d). 0. 022 6 | 16

Using the Binomial Table 1) Locate the number of trials, n. 2) Locate the number of successes, r. 3) Follow that row to the right to the corresponding p column. Copyright © Cengage Learning. All rights reserved. 6 | 17
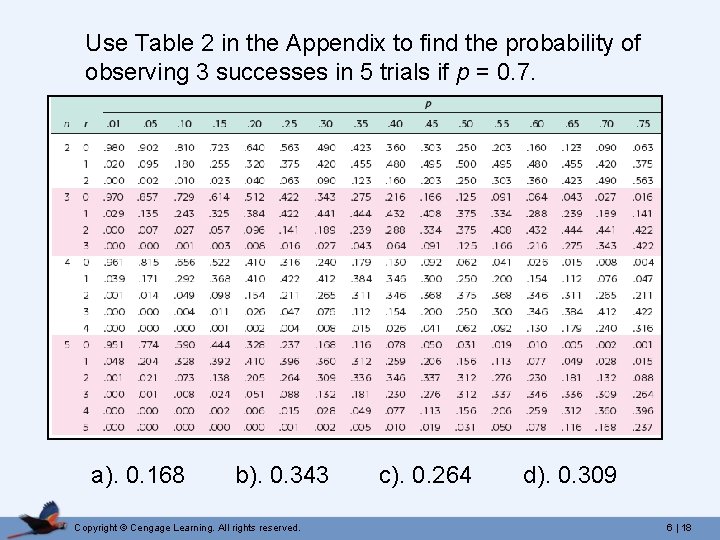
Use Table 2 in the Appendix to find the probability of observing 3 successes in 5 trials if p = 0. 7. a). 0. 168 b). 0. 343 Copyright © Cengage Learning. All rights reserved. c). 0. 264 d). 0. 309 6 | 18
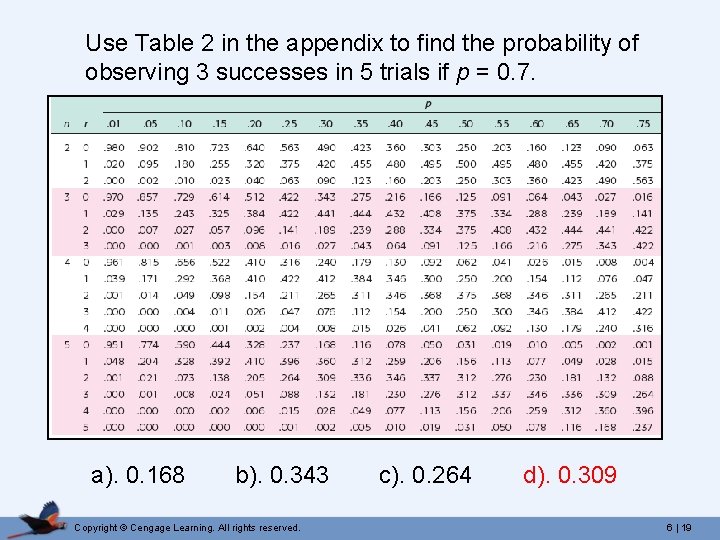
Use Table 2 in the appendix to find the probability of observing 3 successes in 5 trials if p = 0. 7. a). 0. 168 b). 0. 343 Copyright © Cengage Learning. All rights reserved. c). 0. 264 d). 0. 309 6 | 19

Binomial Probabilities • At times, we will need to calculate other probabilities: • P(r < k) • P(r ≤ k) • P(r > k) • P(r ≥ k) where k is a specified value less than or equal to the number of trials, n. Copyright © Cengage Learning. All rights reserved. 6 | 20

Graphing a Binomial Distribution Copyright © Cengage Learning. All rights reserved. 6 | 21

Mean and Standard Deviation of a Binomial Distribution Copyright © Cengage Learning. All rights reserved. 6 | 22

Mean and Standard Deviation of a Binomial Distribution Calculate the standard deviation of a binomial population with n = 100 and p = 0. 3. a). 21 b). 9 Copyright © Cengage Learning. All rights reserved. c). 4. 5825 d). 4. 41 6 | 23

Mean and Standard Deviation of a Binomial Distribution Calculate the standard deviation of a binomial population with n = 100 and p = 0. 3. a). 21 b). 9 Copyright © Cengage Learning. All rights reserved. c). 4. 5826 d). 4. 41 6 | 24

Critical Thinking • Unusual values – For a binomial distribution, it is unusual for the number of successes r to be more than 2. 5 standard deviations from the mean. – This can be used as an indicator to determine whether a specified number of r out of n trials in a binomial experiment is unusual. Copyright © Cengage Learning. All rights reserved. 6 | 25

Critical Thinking • Unusual values – For a binomial distribution, it is unusual for the number of successes r to be more than 2. 5 standard deviations from the mean. A particular binomial experiment has a mean of 14 and a standard deviation of 2. Which of the following is not an unusual number of successes? a). 16 c). 10 b). 17 d). None of these are unusual. Copyright © Cengage Learning. All rights reserved. 6 | 26

Critical Thinking • Unusual values – For a binomial distribution, it is unusual for the number of successes r to be more than 2. 5 standard deviations from the mean. A particular binomial experiment has a mean of 14 and a standard deviation of 2. Which of the following is not an unusual number of successes? a). 16 c). 10 b). 17 d). None of these are unusual. Copyright © Cengage Learning. All rights reserved. 6 | 27
- Slides: 27