Chapter 6 Stacks The stack abstract data type

Chapter 6 Stacks The stack abstract data type is essentially a list using the LIFO (last-in-first-out) policy for adding and removing elements. The principal stack operations: Ø Create an empty stack. Ø Copy an existing stack. Ø Destroy a stack. Ø Determine whether a stack is empty. Ø Add a new element to a stack. Ø Remove the most recently added element from a stack. Ø Retrieve the most recently added element from a stack. CS 240 Chapter 6 - Stacks Page 21

Example Stack Application #1: The Run-Time Stack When running a program that uses functions, a stack is used to keep track of the function calls, including the status of the variables in each function. CS 240 void swap(int &u, int &v) { int temp = u; u = v; v = temp; } u: 20 30 10 v: 30 10 20 temp: ? temp: 30 20 void reorder(int &a, int &b, int &c) { 10 a: 20 if ((b <= a) && (b <= c)) swap(a, b); 20 b: 30 else if ((c <= a) && (c <= b)) swap(a, c); if (b <= c) 20 30 c: 10 swap(b, c); } void main() { int x = 20; int y = 30; int z = 10; if ((x > y) || (y > z)) reorder(x, y, z); cout << x << y << z; } Chapter 6 - Stacks x: x: 10 20 ? x: 20 10 y: y: 30 30 20 ? 20 y: 10 z: z: 30 ? z: 10 20 30 Page 22

Example Stack Application #2: Converting Infix To Postfix When this is found in the infix expression. . . … do this! The beginning of the infix expression Start reading the expression An operand Append it to the postfix expression A right parenthesis Repeatedly pop the stack, appending each entry to the postfix expression, until a left parenthesis is popped (but not output) The end of the infix expression Repeatedly pop the stack, appending each entry to the postfix expression A left parenthesis Push it onto the stack A * or / operator Repeatedly pop the stack, appending all popped * and / operators to the end of the postfix expression, until something else is popped; push this last item back onto the stack, followed by the new * or / that was encountered A + or - operator Repeatedly pop the stack, appending all popped +, -, *, and / operators to the end of the postfix expression, until something else is popped; push this last item back onto the stack, followed by the new + or - that was encountered Following these rules, then, the infix expression 7 + 6 - 3 * ( 5 + 8 / 2 ) is converted into the postfix expression 7 6 + 3 5 8 2 / + * CS 240 Chapter 6 - Stacks Page 23

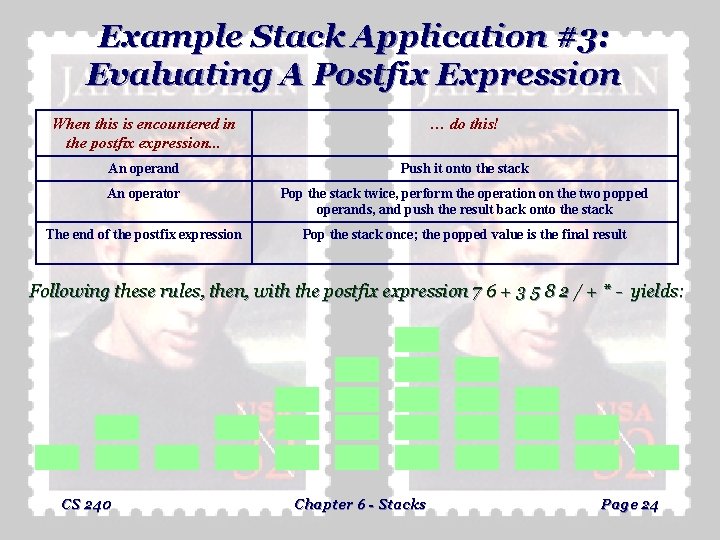
Example Stack Application #3: Evaluating A Postfix Expression When this is encountered in the postfix expression. . . … do this! An operand Push it onto the stack An operator Pop the stack twice, perform the operation on the two popped operands, and push the result back onto the stack The end of the postfix expression Pop the stack once; the popped value is the final result Following these rules, then, with the postfix expression 7 6 + 3 5 8 2 / + * - yields: 2 6 7 7 CS 240 13 8 8 4 5 5 9 3 3 3 27 13 13 Chapter 6 - Stacks -14 Page 24

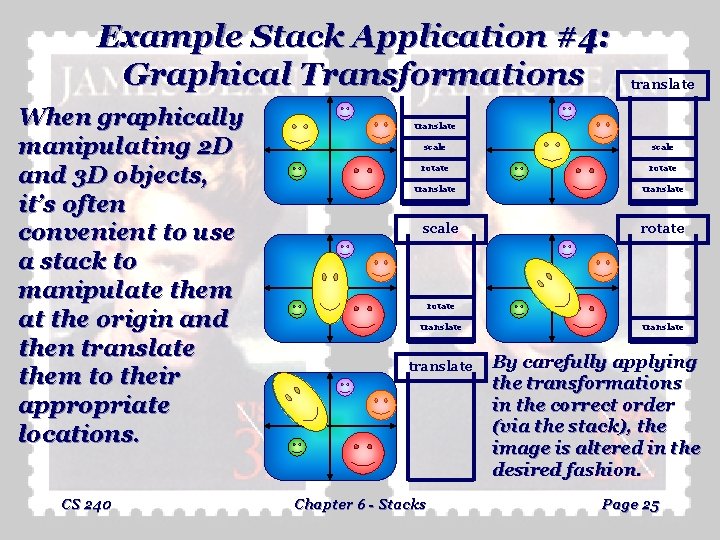
Example Stack Application #4: Graphical Transformations When graphically manipulating 2 D and 3 D objects, it’s often convenient to use a stack to manipulate them at the origin and then translate them to their appropriate locations. CS 240 translate scale rotate translate Chapter 6 - Stacks translate By carefully applying the transformations in the correct order (via the stack), the image is altered in the desired fashion. Page 25

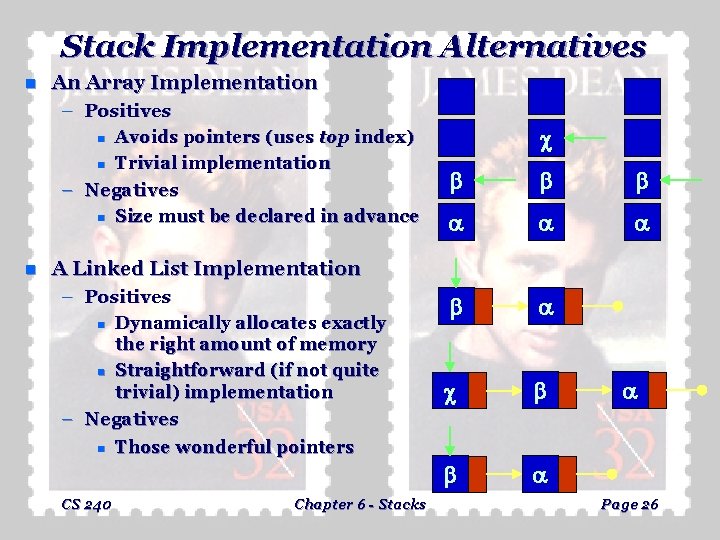
Stack Implementation Alternatives n An Array Implementation – Positives n n Avoids pointers (uses top index) Trivial implementation – Negatives n n Size must be declared in advance A Linked List Implementation – Positives n n Dynamically allocates exactly the right amount of memory Straightforward (if not quite trivial) implementation c b b b a a a b a c b b a a – Negatives n CS 240 Those wonderful pointers Chapter 6 - Stacks Page 26

Linked List Implementation of Stack // Class declaration file: stack. h // Linked List implementation of the // stack ADT – inherits from Linked. List. #ifndef STACK_H #include "linked. List. h" #include <iostream> using namespace std; class stack : protected Linked. List { public: // Class constructors stack(); stack(const stack &s); The stack class “inherits” from the Linked. List class, so all Linked. List members are accessible to any stack. This derived class has a “protected” access specifier, indicating that the public and protected members of Linked. List are considered protected in the stack class. If the access specifier were “private”, then the public and protected members of Linked. List are considered private in // Member functions the derived class. bool is. Empty(); If the access specifier were “public”, void push(const element. Type &item); then the public and protected members element. Type pop(); of Linked. List are considered public and element. Type retrieve(); protected (respectively) in the derived }; class. #define STACK_H Let’s assume that the get. Node and head members in #endif Linked. List were declared protected, not private! Let’s also assume that the element. Type typedef occurred in the Linked. List definition! CS 240 Chapter 6 - Stacks Page 27

// Class implementation file: stack. cpp // Linked List implementation of the // stack ADT – inherits from Linked. List. #include "stack. h" #include "linked. List. h" #include <cassert> #include <cstdlib> using namespace std; // Default constructor: // // Inherited from Linked. List. // stack: : stack(): Linked. List() {} // Copy constructor: // // Inherited from Linked. List. // stack: : stack(const stack &s): Linked. List(s) {} // Empty function: returns a boolean // // value that indicates whether or // // not the stack is empty. // bool stack: : is. Empty() { return head == NULL; } CS 240 // Push function: inserts item at // // the top of the stack. // void stack: : push(const element. Type &elt) { node. Ptr new. Head = get. Node(elt); assert(new. Head != NULL); new. Head->next = head; head = new. Head; return; } // Pop function: removes and returns the // top stack entry (if there is one). element. Type stack: : pop() { element. Type elt; node. Ptr old. Head; assert(head != NULL); old. Head = head; elt = head->item; head = head->next; delete old. Head; return elt; } // // // On_top function: returns (w/o removing) // // the top stack entry (if there is one). // element. Type stack: : retrieve() { element. Type elt; assert(head != NULL); elt = head->item; return elt; } Chapter 6 - Stacks Page 28