Chapter 6 Stability Analysis of Linear Systems REFERENCES

Chapter 6 Stability Analysis of Linear Systems

REFERENCES 1. La. Salle, J. P. , Stability by Lyapunov direct method, New York: Academic Press, 1961. 2. Hahn, W. , Stability of motion, New York, Springer. Verlag, 1967. 3. Desoer, C. A. and Vidyasagar, M. , Feedback systems: Input-output properties, New York: Academic Press, 1975.

The actual systems always work in an environment with various chanciness and continuous disturbance. In addition, the mathematical model used to describe a system is always an approximate one, which results from measure error or omission of some factors. Therefore, stability analysis is a very important research topic for linear systems.

Preliminary knowledge: condition of existence and uniqueness of the solution of differential equation; continuous dependence of solution on initial values. 1. Solutions of differential equations. Consider the following differential equation: Its solution is a function of t and changes with different t 0 and x 0. Hence, it can be expressed as

2. Lipschitz condition: f(x, t) is defined on that . If there exists a constant L such for all , then f is said to satisfy the Lipschitz condition on. This definition can be used in any finite dimensional space. Remark: The Lipschitz condition can guarantee the existence and uniqueness of the solution of a large class of 5 differential equations.

3. The existence, uniqueness and dependence on continuity of initial value of the solution Theorem 1 (existence and uniqueness theorem): Consider the following differential equation Suppose f (x, t) is continuous on W I and satisfies Lipschitz condition, then for any initial condition (x 0, t 0) W I， there always exists a constant a>0 such that there is a unique solution on [t 0 a, t 0+a], which is continuous in t and satisfies the initial condition x(t 0)=x 0.

Theorem 2 (continuous dependence on initial value of solution): Under the condition of Theorem 1, if f (x, t) is continuous and satisfies Lipschitz condition, then the solution of differential equation x(t, t 0, x 0) as a function of t, t 0, x 0, is continuous in its existence region, i. e. , 0, 0, such that, when ‖x (t 0)‖ , we have ‖x(t, t 0, x(t 0)) (t, t 0, (t 0))‖ , a≤t≤b , a≤ t 0 ≤b The above theorem says that: If at the primary instant t 0, x (t 0) is close to (t 0), then x(t) will be close to (t) in [a, b].

§ 6 -1 Lyapunov Stability Lyapunov stability is a generalization of the concept of continuous dependence on initial value of differential equations in the infinite time interval. Hence, we always assume that the differential equation has solution on [t 0, + ). 1. Stability of equilibrium state 1). Equilibrium Consider the following system

If the state x=xe does not change with time (i. e. it is a constant), then the state is said to be an equilibrium of the system. Since an equilibrium is a state of system, it is also a solution of the above differential equation, i. e. a solution of. Example: Consider the differential equation. It is clear that is one of its solutions and it is also an equilibrium.

2. Definition of Lyapunov stability Definition 6 -1 The equilibrium state is said to be stable (Lyapunov stability) if for any ＞ 0 there exists a (t 0, ) 0 such that ‖x(t, t 0, x 0) 0‖＜ ‖x(t 0) 0‖ ‖x(t, t 0, x 0) ‖＜ t≥ t 0 when‖x(t 0) ‖＜ (t 0, ). Definition 6 -2 If in Definition 6 -1, = ( ), i. e. is independent of t 0 (it is uniform in t 0)，then the equilibrium is said to be uniformly stable.

Figure expression of Definition 6 -1(in the sense of Lyapunov) For any ＞ 0, there exists a (t 0, ) 0 such that ‖x(t, t 0, x 0) ‖＜ t≥ t 0 for any ‖x(t 0) ‖＜ (t 0, ). x(t 0 t 1. change with and t 0 at here; ) 2. ‖x(t, t 0, x 0) ‖＜ t≥ t 0 The change of the solution can be arbitrarily small (not no change) when the change of initial value is sufficiently small; 3. It is clear that (t , )< . t 0

Stability in the sense of Lyapunov x(t) x 0 (t 0 , ) Definition 6 -1 For any ＞ 0 there exists a (t 0, ) 0 such that ‖x(t, t 0, x 0) ‖＜ t≥ t 0 when‖x(t 0) ‖＜ (t 0, ). 12

Example: Consider the stability and uniform stability of the following system Its solution is It is clear that

Hence, for any given and satisfy , let (independent of t 0), when we have Hence, the system is stable (in the sense of Lyapunov). Because i. e. it is independent of t 0, the system is also uniformly stable. Here, denotes the 1 -norm of a vector. 14

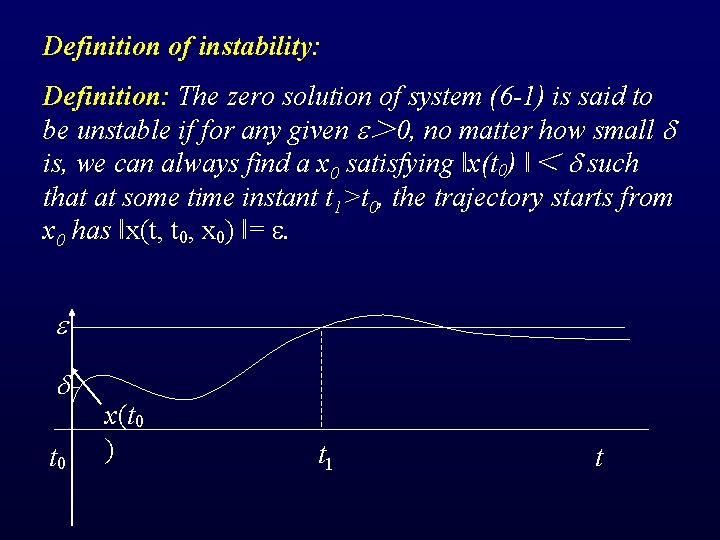
Definition of instability: Definition: The zero solution of system (6 -1) is said to be unstable if for any given ＞ 0, no matter how small is, we can always find a x 0 satisfying ‖x(t 0) ‖＜ such that at some time instant t 1>t 0, the trajectory starts from x 0 has ‖x(t, t 0, x 0) ‖= . t 0 x(t 0 ) t 1 t

Definition 6 -3 x=0 is said to be asymptotically stable if (a) x=0 is stable; (b) there exists a (t 0) 0 and for any ＞ 0 there exists T( , t 0, x 0) such that ‖x(t 0) ‖＜ (t 0) and t t 0 + T( , t 0, x 0) imply ‖x(t, t 0, x 0) ‖＜ . (t 0) (a) x=0 is stable, and the state of x at t t 0 is determined; (b) It is the property when t is sufficiently large. t 0 + T( , t 0, x 0) 1. (t 0) is a fixed region called attraction region and it is not arbitrarily small; T is said to be attraction time or decay time;

2. ‖x(t, t 0, x 0) ‖＜ ，t t 0 + T( , t 0, x 0). Remark: 1) The second part (b) of Definition is said to be attractive about zero solution, which reflects the convergence property of solutions. It also can be rewritten as (t 0) 0, such that ‖x(t 0) ‖＜ (t 0) implies 2) Stability (a) and attraction (b) are two different concepts. For a general system, the two properties have no relationship with each other. A popular counterexample indicates that its solution of differential equation is attractive but not stable.

3) The positive number (t 0) is said to be asymptotic attraction region. If the attraction region is the whole space, then the system is said to be globally asymptotically stable about origin. Definition 6 -4 x=0 is said to be uniformly asymptotically stable if a) x=0 is uniformly stable; b) for every >0 there exists a 0 0 and a T( ) such that ‖x(t, t 0, x 0) ‖＜ for all ‖x(t 0) ‖＜ 0 and t t 0 + T( ), i. e. where the uniformity means that 0 is independent of t 0 and T is independent of t 0 and x 0.

Definition 6 -5 x=0 is exponentially stable if for any ＞ 0, there exists a ＞ 0 and a ( )＞ 0 such that‖x(t 0)‖＜ ( ) implies ‖x(t, t 0, x 0) ‖＜ e (t t 0) t≥ t 0. It is clear that the above definition is uniform in t 0 and x 0. The definitions of stability, uniform stability, asymptotic stability, uniform asymptotic stability and exponential stability here all local concepts, i. e. the conditions of those definitions can only hold near x=0. In engineering, especially in control systems, the initial errors are not always arbitrarily small, but bounded or arbitrarily large. Fortunately, there is no effect on the linear systems we study.

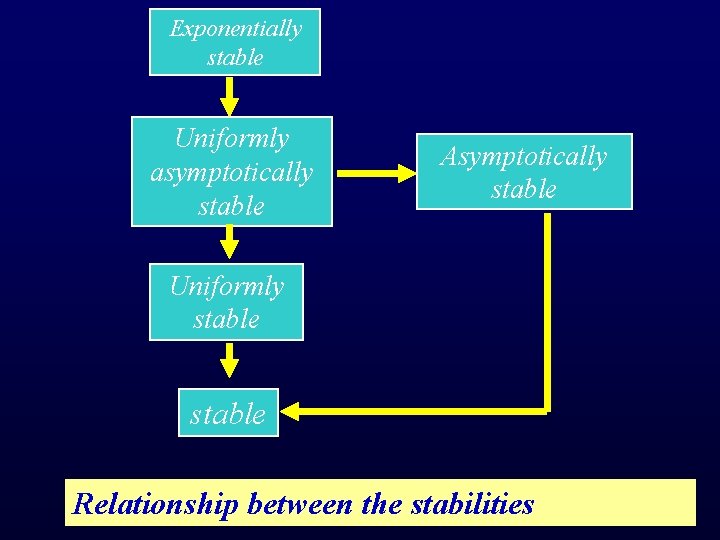
Exponentially stable Uniformly asymptotically stable Asymptotically stable Uniformly stable Relationship between the stabilities

Example: Determine the stability the following system Because it is a time-invariant system, from the Laplace transformation, it is easy to compute. Note that It is clear that for any implies , if we choose , then . Hence, the system is stable in the sense of Lyapunov. Because independent of t 0, the system is also uniformly is

stable. Due to the system is not asymptotically stable, where denotes the 2 -norm of a vector. Example: Which stability the following system is? We can easily figure out that For any Because , if we choose , then implies , hence, the zero-solution is uniformly stable.

the zero-solution is asymptotically stable. On the other hand, when , if for all , the equation holds, then the following equation must hold. This means that T is dependent of t 0 and therefore, the system is not uniformly asymptotically stable.

2. Stability of trajectory In the forgoing sector, we have introduced the stability of equilibrium. Now, let us consider the stability of any trajectory of the following system (6 -1) We know that the solution is uniquely determined by the initial condition. A system may have different trajectories under different conditions. Now, consider the stability of a trajectory of (6 -1): which is said to be a given motion or undisturbed motion.

Example: Consider the following differential equation If we are interested in the motion with initial condition x 10=0. 5: then it is said to be a given motion or undisturbed motion. Compared with the given motion, other motions are all said to be disturbed motions. 25

Example: Consider the system Suppose the given motion is the response of the system with initial condition x(0)=0: then the responses of the system with non-zero initial condition are all said to be disturbed motion. It is clear that the given motion can be considered as a forgoing studied “zero-solution”. 26

Suppose at the initial time t 0, the system is disturbed and the sate x 10 is transformed into x 10+y 0 the motion with that initial condition i. e. the solution of is said to be disturbed motion. Same as the stability of equilibrium (stability in the sense of Lyapunov, uniform stability, asymptotic stability and so on), we can also define the stability of a given motion (stability in the sense of Lyapunov, uniform stability, asymptotic stability and so on).

Definition The trajectory x 1(t, t 0, x 10) is said to be stable (in the sense of Lyapunov) if for any ＞ 0 there exists a (t 0, ) 0 such that‖x(t 0) –x 1(t 0) ‖＜ (t 0, ) implies ‖x(t, t 0, x 0) – x 1(t, t 0, x 10) ‖＜ t≥ t 0 It need to be pointed that the definition of the given motion can be transformed into the problem of stability of equilibrium and therefore, the above definition is unnecessary. 28

Consider the transformation y=x –x 1, then the equation of the disturbance is defined as: It is clear that which means that the problem of stability of the given motion can be transformed into a problem of stability of zero solution of (6 -3), i. e. , when we study the stability of a motion, we can write out its disturbance equation and then study the stability of the zero-solution of disturbance equation (6 -3) and it is not necessary to give the definition of stability of motion.

3. Properties of stability of linear systems Because the corresponding homogeneous equation of the differential equation (6 -4) has a simple structure, it has simple properties in stability. Theorem 6 -1 Consider the linear system (6 -4), if one of its motion is stable, then all the motions are stable. Therefore, in general, we can say ’the system is stable’ for linear systems, while nonlinear systems do not have this property.

Proof 1) Suppose the motion x 1(t) of (6 -4) is stable, i. e. for any ＞ 0, the motions of system (6 -4) making ‖x(t 0) – x 1(t 0) ‖＜ (t 0, ) hold satisfy ‖x(t)– x 1(t) ‖＜ ， t≥ t 0 hand, Let (A-1) On the other . The related equation (disturbance equation) is equivalent to@p 38

upon that, from expression, stability of motions about x 1 is equivalent to the zero-solution stability of ‖x 0(t 0) ‖＜ (t 0, ) ‖x(t 0) – x 1(t 0) ‖＜ (t 0, )， ‖x 0(t) ‖＜ ‖x(t)– x 1(t) ‖＜ ， t≥ t 0 2) Now, let y 1(t) be another motion of system (6 -4), y(t) be an arbitrary motion of (6 -4). Because 32

‖y(t 0) y 1(t 0) ‖＜ (t 0, ), implies ‖ y(t 0) y 1(t 0) ‖＜ ， t≥ t 0 where, is the same as it is in Equation (A-1). By comparing Equations (A-2) @p 36 and (A-3), it is clear that they have the same form and therefore, their stabilities are same too. Q. E. D

Conclusion From the above analysis, the study of stability of linear system at arbitrary initial condition and u is equivalent to the study of stability of zero-solution of the corresponding homogeneous equation

Example: Consider the stability of the following system From the above conclusion, we only need to study the stability of zero-solution of the corresponding homogeneous equation. Because the homogeneous equation is asymptotically stable, the original system is asymptotically stable. In addition, noting that the response of the system is unbounded that is because the input of the system is unbounded, it is not the same concept with the stability of the system.

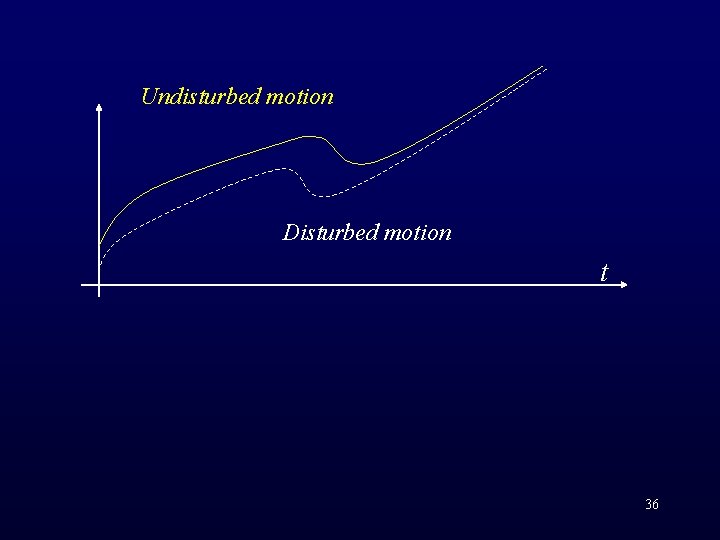
Undisturbed motion Disturbed motion t 36

4. Criterion of stability of linear system Because the stability of linear dynamic system is equivalent to the stability of zero-solution of the corresponding homogeneous equation, we only study the stability of zero-solution of homogeneous equation: Note that A(t) is not a constant matrix. Therefore, we study the stability of motion by using the state transition matrix Φ(t, t 0) but not the eigenvalue. Example 6 -2 consider the following homogeneous equation

The eigenvalues of A are 1, 1. As long as x 2(0) 0, ‖x(t)‖diverges to infinity as t . Hence, the zero-solution is unstable. Therefore, it is incorrect to check the stability from the eigenvalues, which may result in a wrong conclusion.

Theorem 6 -2 Suppose A(t) is a continuous or piecewise continuous function matrix, then the following sufficient and necessary condition holds: 1) ((6 -5)) is stable there exists some constant N(t 0) such that for any t 0 and t≥ t 0, ‖ Φ(t, t 0) ‖≤ N(t 0) （6 -6） 2) （6 -5）is uniformly stable N(t 0) is independent of t 0 in 1). 3) （6 -5) is asymptotically stable 4) (6 -5) is uniformly asymptotically stable there exist N and C >0 such that for any t 0 and t≥ t 0,

Definition: The zero solution of is said to be globally (uniformly) asymptotically stable if the zero solution is (uniformly) asymptotically stable and for any initial condition. Example: The system is globally stable. The properties (3) and (4) in theorem 6 -2 indicate that for the linear system , if its zero-solution is (uniformly) asymptotically stable, then the motion trajectory with any initial condition will converge to the origin, i. e. the attraction region of the origin is the whole state space. 40

Proof of Theorem 6 -2: 1) dx/dt=A(t)x(t) (6 -5) is stable there exists some constant N(t 0) such that the following inequality holds for any t 0 and t≥ t 0, ‖ Φ(t, t 0) ‖≤ N(t 0) Sufficiency: Note that If then (6 -6)

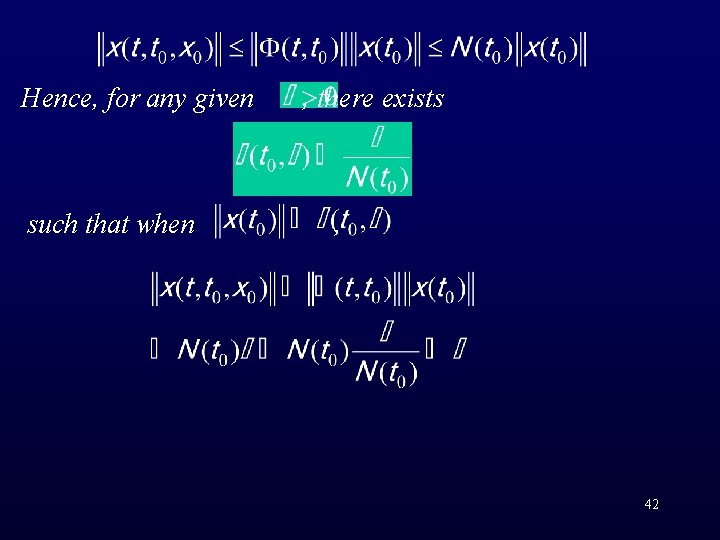
Hence, for any given such that when , there exists , 42

Necessity: Because the zero-solution x=0 is stable, for any given >0, there exists a (t 0, )>0 such that ‖ x(t 0)‖< implies ‖ Φ(t, t 0)x 0‖< t≥ t 0 Let It is clear that ‖ x 0‖ /2< . The jth column of Φ(t, t 0) is Hence, is bounded. Following the same method, we can prove that all the columns are bounded, which implies that Φ(t, t 0) is 43 bounded. Q. E. D

2) dx/dt=A(t)x(t) （6 -5）is uniformly stable in 1), N(t 0) is independent of t 0: ‖ Φ(t, t 0) ‖≤ N （6 -6） Proof: Refer to 1). 3) (6 -5) is asymptotically stable Sufficiency: Because Φ(t, t 0) 0 (t ) there exists a constant N(t 0) such that ‖ Φ(t, t 0) ‖≤ N(t 0) ， t≥ t 0 44

It is known from 1) that the zero-solution x=0 is stable. Using the relationship x(t)= Φ(t, t 0)x 0 from Φ(t, t 0) 0 (t ), we have x(t )=x(t, t 0, x 0) =Φ(t, t 0)x 0 0 (t ) i. e. the zero solution has attraction region. Necessity: Because the zero-solution x=0 has attraction region, there exists a (t 0) such that ‖ x(t 0)‖< (t 0) implies Let x(t)=Φ(t, t 0)x 0 0 (t ) 45

(x(t) is linearly independent of x 0, which indicates that is independent of x 0, i. e. the system is globally asymptotically stable. ) Let 46

(4) is uniformly asymptotically stable there exist N and C >0 such that for any t 0 and t≥ t 0 Sufficiency: Suppose the following condition holds For any given and , there exists which is independent of t 0, such that

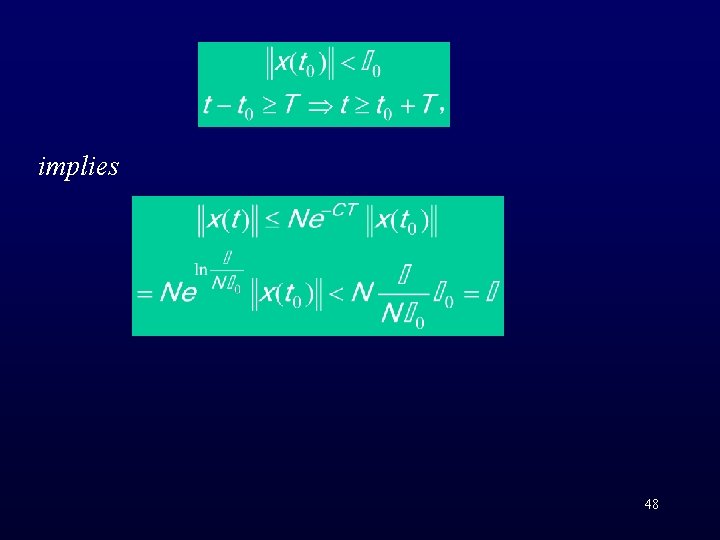
implies 48

Necessity: Suppose the system is uniformly asymptotically stable, we shall prove that Because the system is uniformly stable, it is uniform in t 0 that From the definition of uniform asymptotic stability, is uniform in t 0 and x 0, and

is uniform in t 0. Then, there exists a T ( )>0, such that holds for any t 0. Hence, 50

Form the equation (s-1): we can obtain the first one. Form the equation (*): we can obtain the last one. 2) From Equation (s-1), for any positive integer n, More generally, we have

where Equation (*) has been used repeatedly. For , we have where the former equation has used Equation (s-2) and the later equation has used Equation(s-3).

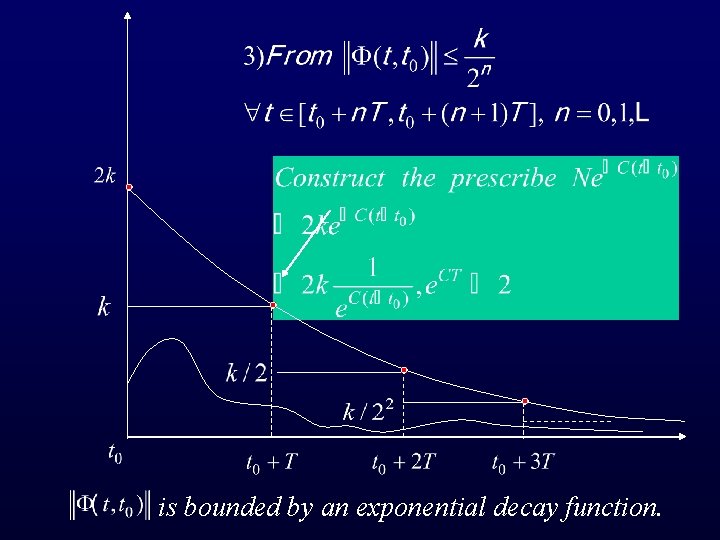
is bounded by an exponential decay function.

In general, we introduce the following positive numbers N and C From the above figure, it is easy to get the inequality Q. E. D

Example: Consider the stability of the following system From the above equation, we have According to Theorem 6 -2, the stability can be checked by the state transition matrix: 55