Chapter 6 Sorting 1 Sorting n A file

Chapter 6 Sorting 1

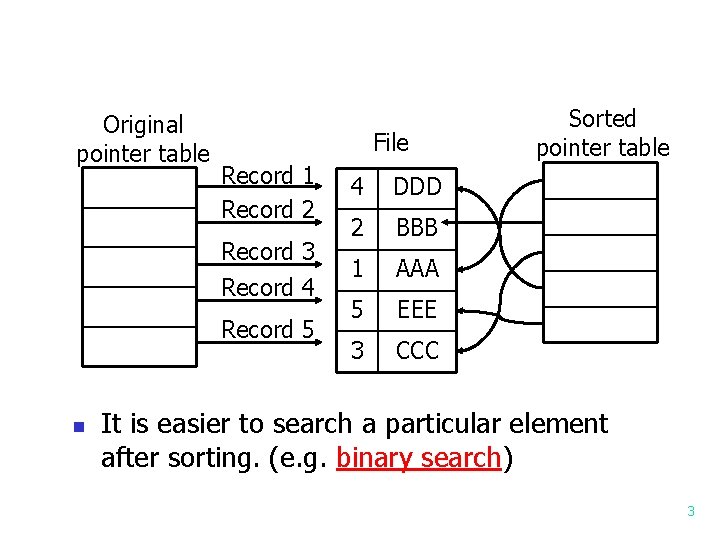
Sorting n A file of size n is a sequence of n items. Each item in the file is called a record. Record 1 Record 2 Record 3 Record 4 Record 5 Key 4 2 1 Other fields DDD BBB AAA 5 EEE 3 CCC original file 1 2 3 4 AAA BBB CCC DDD 5 EEE sorted file 2

Original pointer table File Record 1 Record 2 4 DDD Record 3 Record 4 2 BBB 1 AAA 5 EEE 3 CCC Record 5 n Sorted pointer table It is easier to search a particular element after sorting. (e. g. binary search) 3

Types of sorting n n n internal sorting: data stored in main memory ( more than 20 algorithms ) external sorting: data stored in auxiliary storage. stable sorting : the records with the same key have the same relative order as they have before sorting. 4

Time and space efficiency n 10 50 100 500 1, 000 5, 000 10, 000 50, 000 100, 000 500, 000 a = 0. 01 n 2 1 25 100 2, 500 10, 000 250, 000 1, 000 25, 000 100, 000 2, 5000, 000 b = 10 n 100 500 1, 000 5, 000 10, 000 50, 000 100, 000 500, 000 1, 000 5, 000 a+b 101 525 1, 100 7, 500 20, 000 300, 000 1, 100, 000 25, 500, 000 101, 000 2, 505, 000 (a+b) n 2 1. 01 0. 21 0. 11 0. 03 0. 02 0. 01 5

O notation f(n) is O(g(n)) if there exist positive integers a and b such that f(n) ≦a． g(n) for all n ≧b e. g. 4 n 2 + 100 n = O(n 2) ∵ n ≧ 100, 4 n 2+100 n ≦ 5 n 2 4 n 2 + 100 n = O(n 3) ∵ n ≧ 10, 4 n 2+100 n ≦ 2 n 3 f(n)= c 1 nk + c 2 nk-1 +…+ ckn + ck+1 = O(nk+j), for any j ≧ 0 f(n)= c = O(1), c is a constant logmn = logmk． logkn , for some constants m and k logmn = O(logkn) = O(log n) 6

Time complexity n n polynomial order: O(nk), for some constant k. exponential order: O(dn), for some d >1. NP-complete(intractable) problem: requiring exponential time algorithms. best sorting algorithm with comparisons: O(nlogn) 7

nlog 10 n and n 2 1 5 1 5 1 5 1 n × 101 × 102 × 103 × 104 × 105 × 106 × 107 nlog 10 n 1. 0 × 101 8. 5 × 101 2. 0 × 102 1. 3 × 103 3. 0 × 103 1. 8 × 104 4. 0 × 104 2. 3 × 105 5. 0 × 105 2. 8 × 106 6. 0 × 106 3. 3 × 107 7. 0 × 107 1. 0 2. 5 1. 0 n 2 × × × × 102 103 104 105 106 107 108 109 1010 1011 1012 1013 1014 8

Bubble sort n 相鄰兩個資料相比, 若未符合順序, 則對調 (exchange)之. e. g. 8 8 8 9 9 9 2 2 9 9 9 8 8 8 9 9 2 5 5 6 6 6 5 5 5 2 6 6 6 5 5 5 6 6 2 2 2 pass 1 (由大而小sort) decreasing order nonincreasing order pass 2 pass 3 9

Time complexity of bubble sort n 如果在某一個pass中，沒有任何相鄰兩項資料對調， 表示已經sort完畢 n best case : 未sort之前, 已按順序排好, 需 1 pass worst case: 需 n-1 個 pass ( n 為資料量) n 比較(comparison)次數最多為: n n(n-1)+(n-2)+. . . +1 = 2 = O(n 2) Time complexity: O(n 2) 10

void bubble(int x[], int n) { int hold, j, pass; int switched = TRUE; for (pass=0; pass < n-1 && switched == TRUE; pass++){ /*outer loop controls the number of passes */ switched = FALSE; /* initially no interchanges have */ /* been made on this pass */ for (j = 0; j < n-pass-1; j++) /* inner loop governs each individual pass */ if (x[j] > x[j+1]){ /* elements out of order */ /* an interchange is necessary */ switched = TRUE; hold = x[j]; x[j] = x[j+1]; x[j+1] = hold; } /* end if */ } /* end for */ } /* end bubble */ 11

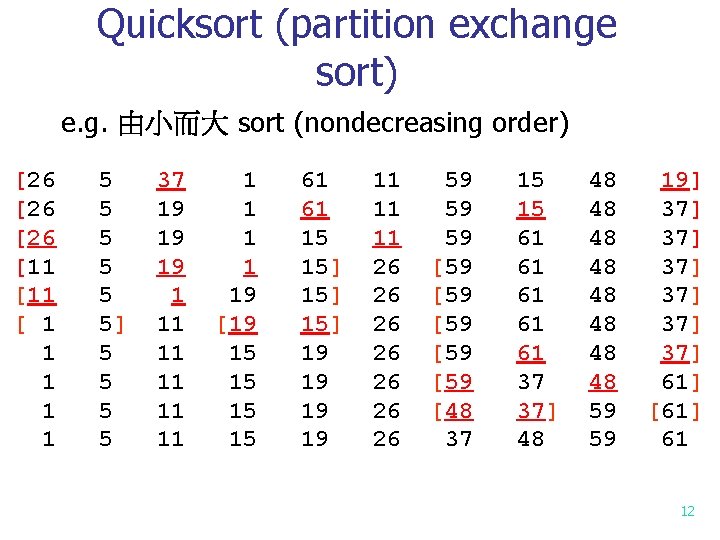
Quicksort (partition exchange sort) e. g. 由小而大 sort (nondecreasing order) [26 [26 [11 [ 1 1 1 5 5 5] 5 5 37 19 19 19 1 11 11 1 1 19 [19 15 15 61 61 15 15] 15] 19 19 11 11 11 26 26 59 59 59 [59 [59 [48 37 15 15 61 61 61 37 37] 48 48 48 59 59 19] 37] 37] 37] 61] [61] 61 12

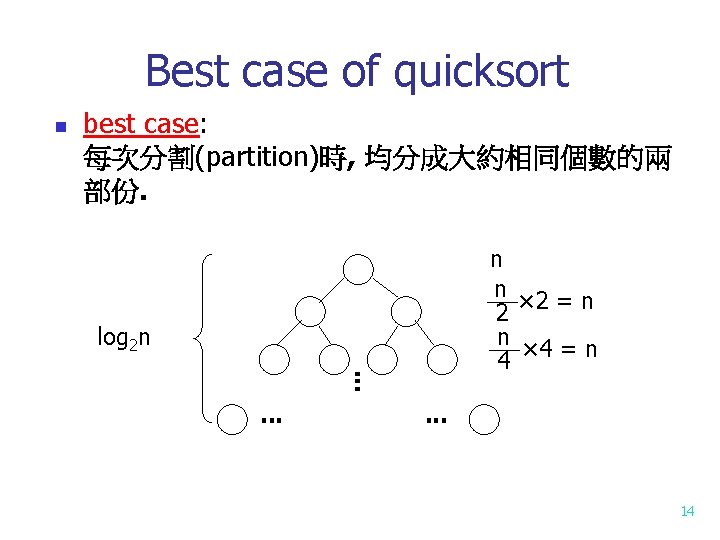
Best case of quicksort n best case: 每次分割(partition)時, 均分成大約相同個數的兩 部份. n n × 2 = n 2 n × 4 = n 4 log 2 n. . 14

Mathematical analysis of best case n T(n): n 個資料所需時間 T(n)≦ cn+2 T(n/2), for some constant c. ≦ cn+2(c．n/2 + 2 T(n/4)) ≦ 2 cn + 4 T(n/4). . . ≦ cnlog 2 n + n. T(1) = O(nlogn) 15

void partition(int x[], int lb, int ub, int *pj) { int a, down, temp, up; a = x[lb]; /* a is the element whose final position */ /* is sought */ up = ub; down = lb; while (down < up){ while (x[down] <= a && down < ub) down++; /* move up the array */ while (x[up] > a) up--; /* move down the array */ if (down < up){ /* interchange x[down] and x[up] */ temp = x[down]; x[down] = x[up]; x[up] = temp; } /* end if */ } /* end while */ x[lb] = x[up]; x[up] = a; *pj = up; 16 } /* end partition */

main program: if (lb >= ub) return; // array is sorted partition(x, lb, ub, j); // partition the elements of the // subarray such that one of the // elements(possibly x[lb]) is // now at x[j] (j is an output // parameter) and: // 1. x[i] <= x[j] for lb <= i < j // 2. x[i] >= x[j] for j < i <= ub // x[j] is now at its final position quick(x, lb, j-1); // recursively sort the subarray // between posiitons lb and j-1 quick(x, j+1, ub); // recursively sort the subarray // between positions j+1 and ub 17

Selection sort e. g. 由大而小 sort n n 8 2 9 5 6 9 9 2 8 8 2 6 6 5 5 6 6 2 2 pass 1 pass 2 pass 3 pass 4 方法: 每次均從剩餘未 sort 部份之資料, 找出最大者(或最 小者), 然後對調至其位置 比較次數: (n-1)+(n-2)+. . . +1 = n(n-1) =O(n 2) 2 Time complexity: O(n 2) 18

Binary tree sort 8 e. g. input data: 8, 2, 9, 5, 6 建立 binary search tree: 2 9 5 inorder traversal: output: 2 5 6 8 9 n worst case: input data: 2, 5, 6, 8, 9 比較次數: 6 2 5 6 8 n best case: time complexity: 9 i*2 i = O(nlogn), d log 2 n 19

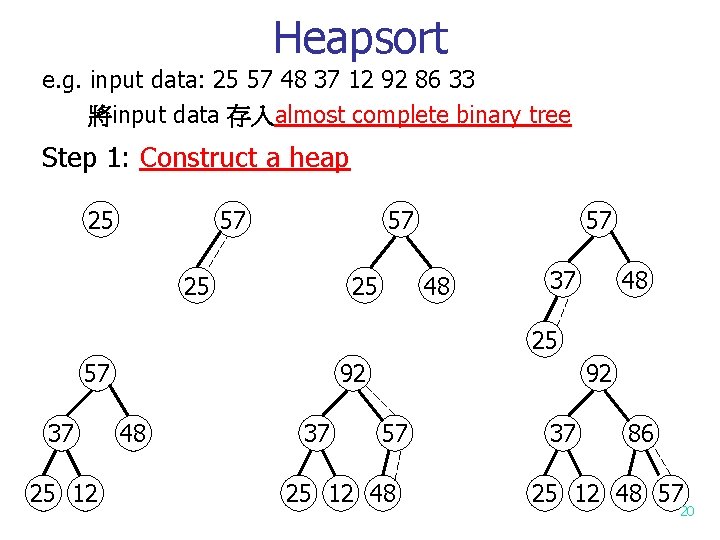
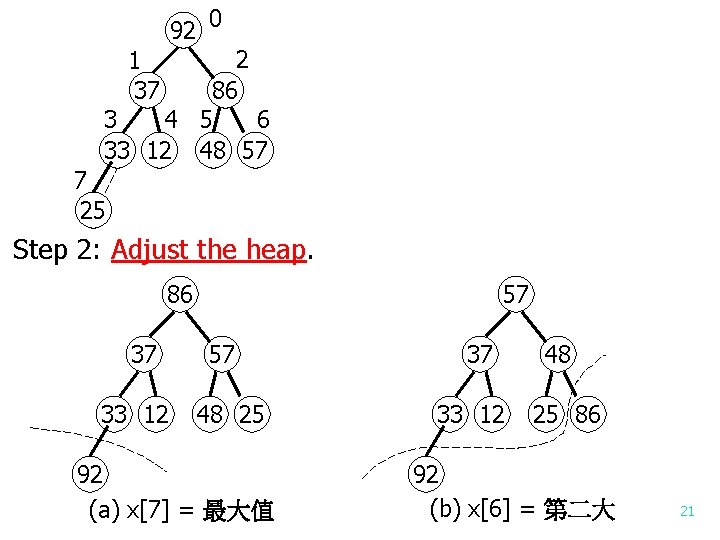
Heapsort e. g. input data: 25 57 48 37 12 92 86 33 將input data 存入almost complete binary tree Step 1: Construct a heap 25 57 57 25 25 57 48 37 48 25 57 37 25 12 92 48 37 92 57 25 12 48 37 86 25 12 48 57 20

92 0 2 86 3 4 5 6 33 12 48 57 1 37 7 25 Step 2: Adjust the heap. 86 37 33 12 57 57 48 25 92 (a) x[7] = 最大值 37 33 12 48 25 86 92 (b) x[6] = 第二大 21

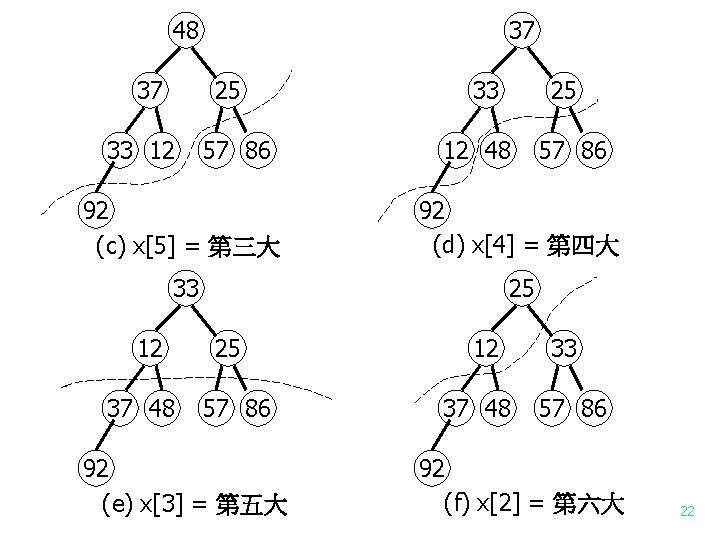
48 37 37 25 33 12 57 86 33 25 12 48 57 86 92 (c) x[5] = 第三大 92 (d) x[4] = 第四大 33 25 12 37 48 25 57 86 92 (e) x[3] = 第五大 12 37 48 33 57 86 92 (f) x[2] = 第六大 22

Final: x[1] x[3] x[7] 37 25 x[0] 12 x[2] 33 x[6] 48 57 86 x[4] x[5] 92 (g) x[1] = 第七大 n n The heapsort should be implemented by an array, not by a binary tree time complexity: O(nlogn) (in the worst case) 23

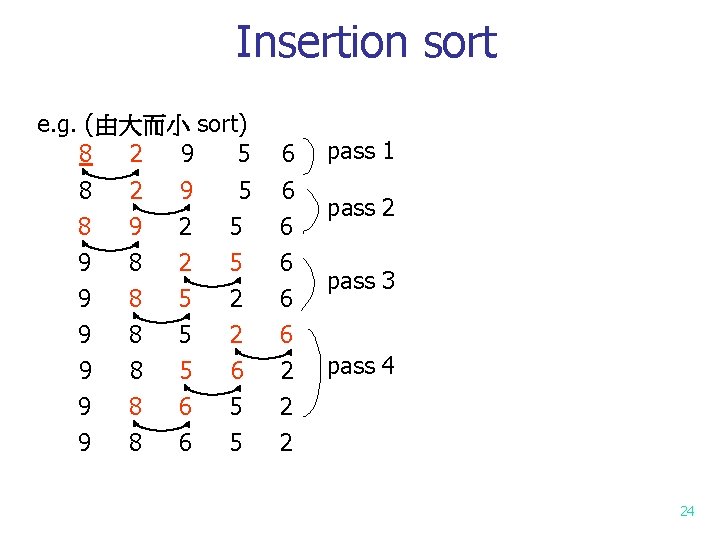
Insertion sort e. g. (由大而小 sort) 8 2 9 5 6 pass 1 pass 2 8 8 2 9 9 2 5 5 6 6 9 9 9 8 8 8 2 5 5 5 6 6 5 2 2 6 5 5 6 6 6 2 2 2 pass 3 pass 4 24

void insertsort(int x[], int n) { int i, k, y; //initially x[0] may be thought of as a sorted //file of one element. After each repetition of //the following loop, the elements x[0] through //x[k] are in order for (k = 1; k < n; k++){ /* Insert x[k] into the sorted file */ y = x[k]; /* Move down 1 position all elements greater*/ /* than y */ for (i = k-1; i >= 0 && y < x[i]; i--) x[i+1] = x[i]; /* Insert y at proper position */ x[i+1] = y; } /* end for */ } /* end insertsort */ 26

e. g. 由大到小 sort 21 11 09 02 16 31 26 01 27 05 13 19 12+1 pass 1: d 1 = =6 2 d 1 26 11 27 05 16 31 21 01 09 02 13 19 d +1 6+1 pass 2: d 2 = 1 = =3 2 2 d 2 26 16 31 21 13 27 05 11 19 02 01 09 d 2+1 pass 3: d 3 = = 3+1 =2 2 2 d 3 31 27 26 21 19 16 13 11 05 09 01 02 d 3+1 2+1 pass 4: d 4 = = 2 =1 2 d 4 31 27 26 21 19 16 13 11 09 05 02 01 28

n 每個 pass 均進行多組的insertion sort. 若一開始 d=1, 則與 insertion sort 完全一樣 Knuth 證明: di-1 = 3 di+1, 即 di= di-1 -1 3 為最好 time complexity: O(nlog 2 n)~O(n 3/2) n 適合數百個資料之 sorting 29

void shellsort (int x[], int n, int incrmnts[], int numinc) { int incr, j, k, span, y; for (incr = 0; incr < numic; incr++){ /* span is the size of the increment */ span = incrmnts[incr]; for (j = span; j< n; j++){ /* Insert element x[j] into its proper */ /* position within its subfile */ y = x[j]; for (k = j-span; k >= 0 && y < x[k]; k -= span) x[k+span] = x[k]; x[k+span] = y; } /* end for */ 30 } /* end shellsort */

address caculation sort (sorting by hashing) . . . e. g. 由小到大 sort input data: 19 13 05 27 01 26 31 16 02 09 11 21 分成 10 個 subfile, 每個 subfile 是一個 linked list, 其資料由小而大排列 01 02 05 09 11 13 16 19 21 26 27 31 假設有 n 個資料, m 個 subfile n ～ best case: 1, 且 uniform distribution ～ m time complexity: O(n) n worst case: >>1, 或 not uniform distribution m time complexity: O(n 2) 31

Two-way merge n n Merge two sorted sequences into a single one. e. g. [25 37 48 57][12 33 86 92] merge [12 25 33 37 48 57 86 92] 設兩個 sorted lists 長度各為 m, n time complexity: O(m+n) 32

Merge sort n e. g. (由小而大) [25] [57] [48] [37] [12] [92] [86] [33] pass 1 [25 57] [37 48] [12 92] [33 86] pass 2 [25 37 48 57] [12 33 86 92] pass 3 [12 25 33 37 48 57 86 92] n n n 需要 log 2 n 個 pass time complexity: O(nlogn) It can be implemented by a recursive function. 33

Radix sort e. g. 由小到大的 sort input data 19 13 05 27 01 26 31 16 02 09 11 21 pass 1 0) 1) 2) 3) 4) 5) 6) 7) 8) 9) merge 01, 31, 11, 21 02 13 05 26, 16 27 19, 09 01 31 11 21 02 13 05 26 16 27 19 09 pass 2 0) 1) 2) 3) 4) 5) 6) 7) 8) 9) 01, 02, 05, 09 11, 13, 16, 19 21, 26, 27 31 merge 01 02 05 09 11 13 16 19 21 26 27 31 34