Chapter 6 SeriesParallel Circuits Topics Covered in Chapter

Chapter 6 Series-Parallel Circuits Topics Covered in Chapter 6 6 -1: Finding RT for Series-Parallel Resistances 6 -2: Resistance Strings in Parallel 6 -3: Resistance Banks in Series 6 -4: Resistance Banks and Strings in Series-Parallel © 2007 The Mc. Graw-Hill Companies, Inc. All rights reserved.

Topics Covered in Chapter 6 § 6 -5: Analyzing Series-Parallel Circuits with Random Unknowns § 6 -6: The Wheatstone Bridge § 6 -7: Troubleshooting: Opens and Shorts in Series. Parallel Circuits Mc. Graw-Hill © 2007 The Mc. Graw-Hill Companies, Inc. All rights reserved.

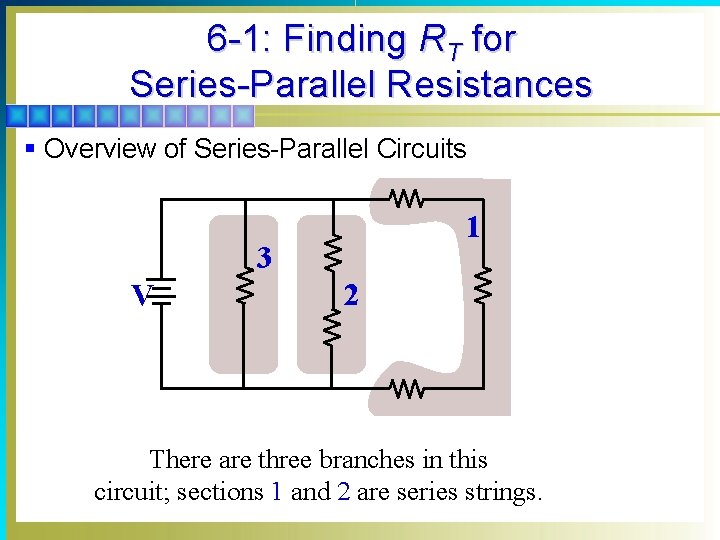
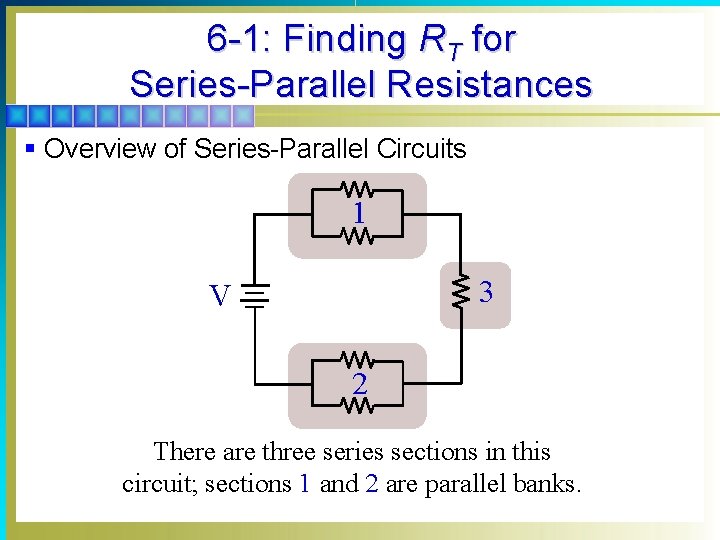
6 -1: Finding RT for Series-Parallel Resistances § Overview of Series-Parallel Circuits § A series-parallel circuit, or combination circuit, combines both series and parallel connections. § Most electronic circuits fall into this category. Series-parallel circuits are typically used when different voltage and current values are required from the same voltage source. § Series components form a series string. § Parallel components form a parallel bank.

6 -1: Finding RT for Series-Parallel Resistances § Overview of Series-Parallel Circuits 1 3 V 2 There are three branches in this circuit; sections 1 and 2 are series strings.

6 -1: Finding RT for Series-Parallel Resistances § Overview of Series-Parallel Circuits 1 3 V 2 There are three series sections in this circuit; sections 1 and 2 are parallel banks.

6 -1: Finding RT for Series-Parallel Resistances § To find RT for a series-parallel circuit, add the series resistances and combine the parallel resistances. § In this diagram, R 1 and R 2 are in series, and R 3 and R 4 are in parallel. However, R 2 is not in series with the parallel resistances: Resistances in series have the same current, but the current in R 2 is equal to the sum of the branch currents I 3 and I 4. Fig. 6 -1 b: Schematic diagram of a seriesparallel circuit. Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

6 -1: Finding RT for Series-Parallel Resistances § For Fig. 6 -1 b, § The series resistances are: 0. 5 kΩ + 0. 5 kΩ = 1 kΩ § The parallel resistances are: 1 kΩ / 2 = 0. 5 kΩ § The series and parallel values are then added for the value of RT: 1 kΩ + 0. 5 kΩ = 1. 5 kΩ

6 -2: Resistance Strings in Parallel § In this figure, branch 1 has two resistances in series; branch 2 has only one resistance. § Ohm’s Law can be applied to each branch, using the same rules for the series and parallel components that were discussed in Chapters 4 and 5. Fig. 6 -3 a: Series string in parallel with another branch (schematic diagram). Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

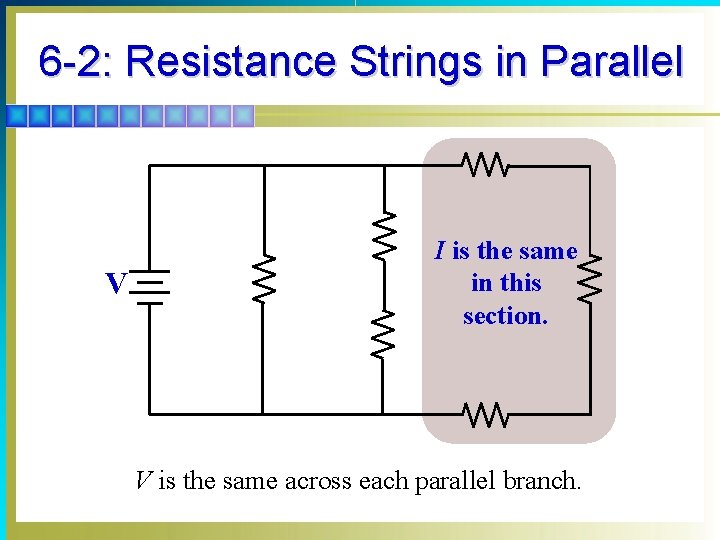
6 -2: Resistance Strings in Parallel § Series Circuit § Current is the same in all components. § V across each series R is I × R. § VT = V 1 + V 2 + V 3 +. . . + etc. § Parallel Circuit § Voltage is the same across all branches. § I in each branch R is V/R. § IT = I 1 + I 2 + I 3 +. . . + etc.

6 -2: Resistance Strings in Parallel V I is the same in this section. V is the same across each parallel branch.

6 -2: Resistance Strings in Parallel § The current in each branch equals the voltage applied across the branch divided by the branch RT. § The total line current equals the sum of the branch currents for all parallel strings. § The RT for the entire circuit equals the applied voltage divided by the total line current. § For any resistance in a series string, the IR voltage drop across that resistance equals the string’s current multiplied by the resistance. § The sum of the voltage drops in the series string equals the voltage across the entire string.

6 -3: Resistance Banks in Series § In this figure, R 2 and R 3 are parallel resistances in a bank. The parallel bank is in series with R 1. § There may be more than two parallel resistances in a bank, and any number of banks in series. § Ohm’s Law is applied to the series and parallel components as seen previously. Fig. 6 -4 a: Parallel bank of R 2 and R 3 in series with R 1 (Original circuit). Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

6 -3: Resistance Banks in Series § To find the total resistance of this type of circuit, combine the parallel resistances in each bank and add the series resistances. R= V I 24 V R= 4 A 24 V 6Ω = 4 A 10 Ω (of R 2 + R 3) + 1Ω (R 1) 6Ω = 2 branches 6Ω = 5Ω + 1Ω

6 -4: Resistance Banks and Strings in Series-Parallel § To solve series-parallel (combination) circuits, it is important to know which components are in series with one another and which components are in parallel. § Series components must be in one current path without any branch points. § To find particular values for this type of circuit, § Reduce and combine the components using the rules for individual series and parallel circuits. § Reduce the circuit to its simplest possible form. § Then solve for the needed values using Ohm’s Law.

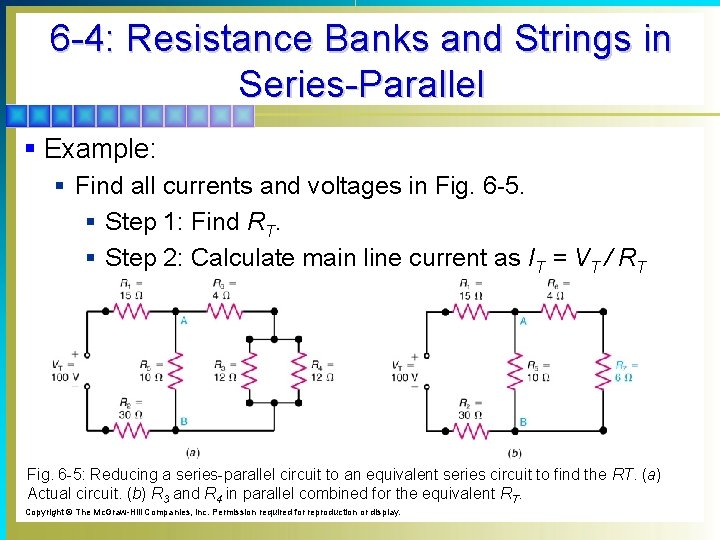
6 -4: Resistance Banks and Strings in Series-Parallel § Example: § Find all currents and voltages in Fig. 6 -5. § Step 1: Find RT. § Step 2: Calculate main line current as IT = VT / RT Fig. 6 -5: Reducing a series-parallel circuit to an equivalent series circuit to find the RT. (a) Actual circuit. (b) R 3 and R 4 in parallel combined for the equivalent RT. Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

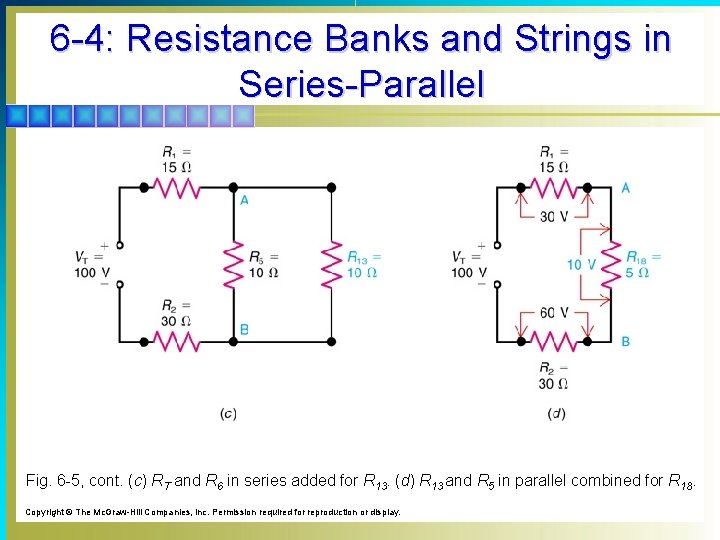
6 -4: Resistance Banks and Strings in Series-Parallel Fig. 6 -5, cont. (c) RT and R 6 in series added for R 13. (d) R 13 and R 5 in parallel combined for R 18. Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

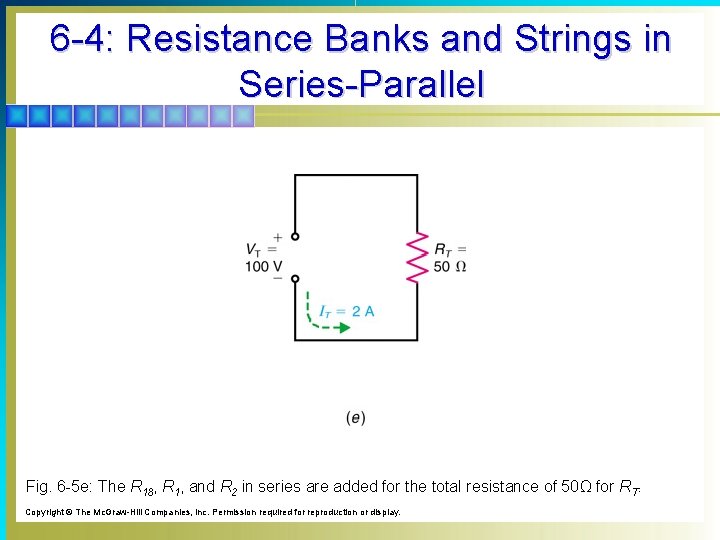
6 -4: Resistance Banks and Strings in Series-Parallel Fig. 6 -5 e: The R 18, R 1, and R 2 in series are added for the total resistance of 50Ω for RT. Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

6 -5: Analyzing Series-Parallel Circuits with Random Unknowns § In solving such circuits, apply the same principles as before: § Reduce the circuit to its simplest possible form. § Apply Ohm’s Law.

6 -5: Analyzing Series-Parallel Circuits with Random Unknowns § Example: § In Fig. 6 -6, we can find branch currents I 1 and I 2 -3, and IT, and voltage drops V 1, V 2, and V 3, without knowing the value of RT. Fig. 6 -6: Finding all the currents and voltages by calculating the branch currents first. Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

6 -5: Analyzing Series-Parallel Circuits with Random Unknowns § Find I 1, I 2 -3, and IT. I 1 = V R 90 V (parallel branches have the same voltage) I 1= 30Ω I 1= 3 A

6 -5: Analyzing Series-Parallel Circuits with Random Unknowns I 2 -3 = V R 90 V I 2 -3 = 20Ω + 25Ω 90 V I 2 -3 = 45Ω I 2 -3 = 2 A IT = I 1 + I 2 -3 IT = 3 A + 2 A IT = 5 A

6 -5: Analyzing Series-Parallel Circuits with Random Unknowns § Find voltage drops V 1, V 2, and V 3: Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

6 -5: Analyzing Series-Parallel Circuits with Random Unknowns V 1 = VA (parallel branches have the same voltage) V 1 = 90 V or V 1 = I 1 R 1 V 2 = I 2 -3 R 2 V 3 = I 2 -3 R 3 V 1 = 3 A × 30Ω V 2 = 2 A(20 Ω) V 3 = 2 A(25 Ω) V 1 = 90 V V 2 = 40 V V 3 = 50 V Note: V 2 + V 3 = VA 40 V + 50 V = 90 V

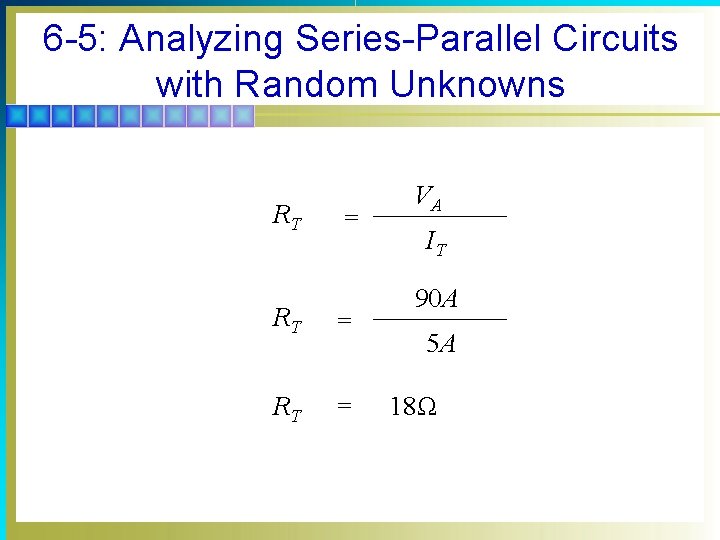
6 -5: Analyzing Series-Parallel Circuits with Random Unknowns RT = VA IT 90 A 5 A 18Ω

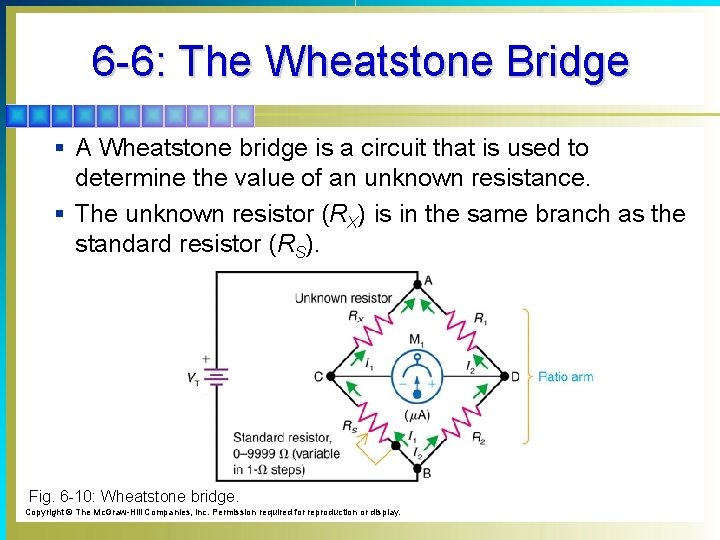
6 -6: The Wheatstone Bridge § A Wheatstone bridge is a circuit that is used to determine the value of an unknown resistance. § The unknown resistor (RX) is in the same branch as the standard resistor (RS). Fig. 6 -10: Wheatstone bridge. Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

6 -6: The Wheatstone Bridge § Resistors R 1 and R 2 form the ratio arm; they have very tight resistance tolerances. § The galvanometer (M 1), a sensitive current meter, is connected between the output terminals C and D. § When R 1 / R 2 = R 3 / R 4, the bridge is balanced. § When the bridge is balanced, the current in M 1 is zero.

6 -6: The Wheatstone Bridge § Using a Wheatstone Bridge to Measure an Unknown Resistance § RS is adjusted for zero current in M 1. . § When the current in M 1 = 0 A, the voltage division between RX and RS is equal to that between R 1 and R 2. Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

6 -6: The Wheatstone Bridge Note: When the Wheatstone bridge is balanced, it can be analyzed as two series strings in parallel. Note the following relationship: R 1 RX = RS R 2 RX R 1 = RS × R 2

6 -7: Troubleshooting: Opens and Shorts in Series-Parallel Circuits § In series-parallel circuits, an open or short in one part of the circuit changes the values in the entire circuit. § When troubleshooting series-parallel circuits, combine the techniques used when troubleshooting individual series and parallel circuits.

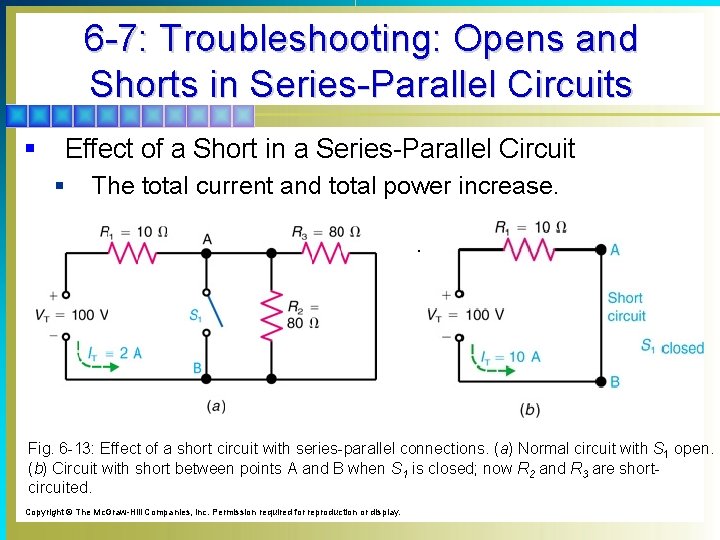
6 -7: Troubleshooting: Opens and Shorts in Series-Parallel Circuits § Effect of a Short in a Series-Parallel Circuit § The total current and total power increase. . Fig. 6 -13: Effect of a short circuit with series-parallel connections. (a) Normal circuit with S 1 open. (b) Circuit with short between points A and B when S 1 is closed; now R 2 and R 3 are shortcircuited. Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

6 -7: Troubleshooting: Opens and Shorts in Series-Parallel Circuits § Effect of a Short in a Series-Parallel Circuit The total current increases from 2 A with S 1 open to 10 A with S 1 closed. Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display. With S 1 closed, R 2 and R 3 are shorted out.

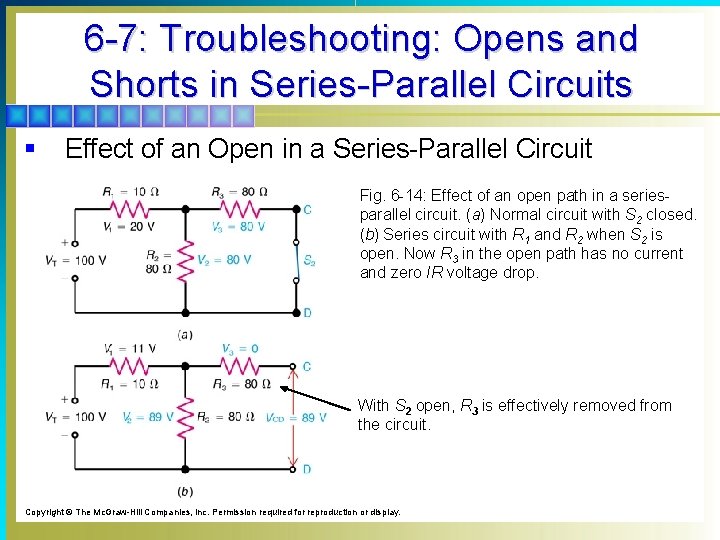
6 -7: Troubleshooting: Opens and Shorts in Series-Parallel Circuits § Effect of an Open in a Series-Parallel Circuit Fig. 6 -14: Effect of an open path in a seriesparallel circuit. (a) Normal circuit with S 2 closed. (b) Series circuit with R 1 and R 2 when S 2 is open. Now R 3 in the open path has no current and zero IR voltage drop. With S 2 open, R 3 is effectively removed from the circuit. Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.

6 -7: Troubleshooting: Opens and Shorts in Series-Parallel Circuits § Effect of an Open in a Series-Parallel Circuit With S 2 open the voltage across points C and D equals the voltage across R 2, which is 89 V. The voltage across R 3 is zero. Copyright © The Mc. Graw-Hill Companies, Inc. Permission required for reproduction or display.