Chapter 6 Rules of Probability 6 1 Sample

Chapter 6 Rules of Probability ¨ 6. 1 Sample spaces and events ¨ 6. 2 Postulates of probabilities ¨ 6. 4 Additive rules ¨ 6. 5 Conditional probability ¨ 6. 6 Multiplication rules ¨ 6. 7 Bayes theorem

6. 1 Sample Spaces and Events ¨ In a probability experiment the possible outcomes form the samples space, S 1. Pick a card and note the suit S={spade, club, heart, diamond} 2. Pick a card and note the color S={red, black} 3. Pick a card and note if it is an ace S={ace, not ace}

More examples 4. Roll a die and note the dots S={1, 2, 3, 4, 5, 6} 5. Roll 2 dice and note the sum S={2, 3, 4, … …, 11, 12}

Event ¨ A subset of a sample space is called an event For example, roll one die. Even={2, 4, 6} Odd= {1, 3, 5} Greater than 6=empty set=

Operations ¨ Union A∪B=all outcomes in A or B ¨ Intersection A∩B=all outcomes in both A and B ¨ Complement A’=all outcomes not in A (like S-A)

Operations of Events ¨ If two events have no outcomes in common they are mutually exclusive (or disjoint) i. e. , A∩ B= S={1, 2, 3, 4, 5, 6} Odd ={1, 3, 5}=A Even={2, 4, 6}=B more than 2={3, 4, 5, 6}=C ‘Odd’ and ‘Even’ are mutually exclusive; ‘Even’ and ‘C’ are not mutually exclusive.

Example 6. 1 ¨ Roll a red die and a white die S= {(i, j): i, j=1, 2, …, 6} A={(i, j): i+j=7}={sum=7} B={(3, j): j=1, . . , 6}={red=3} Get A∪B A∩B A’

Another example ¨ S={52 cards in deck} Club ∪Spade = Black Club ∩Spade= Red Ace= {Ace of hearts, ace of diamond} Red’= Black
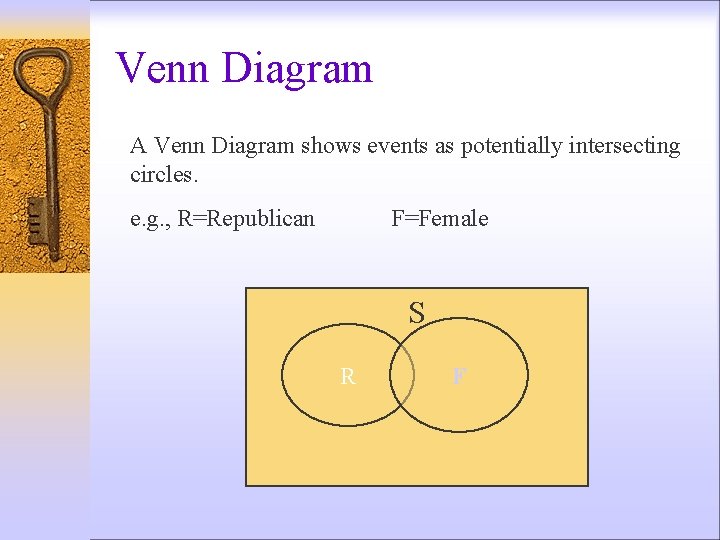
Venn Diagram A Venn Diagram shows events as potentially intersecting circles. e. g. , R=Republican F=Female S R F
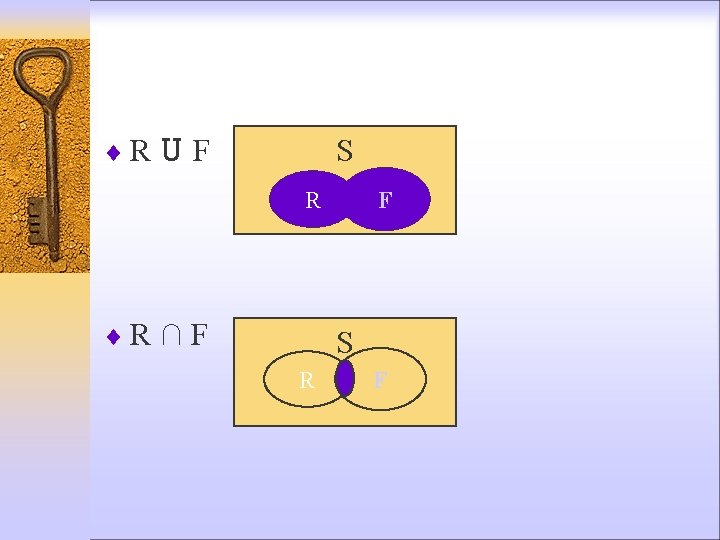
¨R U F S F R ¨R ∩ F S R F

6. 2 Postulates of probabilities ¨ Roll a die S={1, 2, 3, 4, 5, 6} ¨ P(1)=P(2)=…=P(6)=1/6 For any event A: 0 P(A) 1 P(S)=1 P(A’)=1 -P(A)

Example 6. 2 ¨ A={1, 2}, B={ 3, 4} A and B are disjoint. (or mutually exclusive) P(A∪B)=2/6+2/6=2/3 3, 4 B 1, 2 A 5, 6 P(A∪B)=P(A)+P(B) if A and B are mutually exclusive

Example 6. 3 ¨ S={52 cards} P(ace ∪ king)=P(ace or king) =4/52+4/52=2/13 ¨ P(rain)=0. 7 then P(not rain)=1 -0. 7=0. 3

Exercise ¨ Which of the following pairs of events are mutually exclusive? Explain. – A driver getting a ticket for speeding and a ticket for going through a red light. – Being foreign-born and being President of the United States. – A person wearing black shoes and green socks. – Having rain and sunshine on the 4 th of July, 2005.

Exercise ¨ If A and B are the events that Consumer Union will rate a car stereo good or poor, P(A)=0. 24 and P(B)=0. 35, determine the following probabilities: – P(A’) – P(AUB) – P(A ∩B)

Exercise ¨ Let E, T, and N be the events that a car brought to a garage needs an engine overhaul, transmission repairs, or new tires. Draw a Venn diagram for the following –EUTUN – E ∩T ∩N’

6. 3. Probability and odds-skip

6. 4 Addition Rules ¨ For mutually exclusive events P(A 1∪A 2 ∪ • • • ∪Ak)=P(A 1)+P(A 2)+ • • • +P(Ak) P(ace or king or queen) =P(ace)+P(king)+P(queen) =4/52+4/52=3/13

When individual outcomes are mutually exclusive, The probability of an event A is the sum of the probabilities for all outcomes in A For a dice, S={1, 2, 3, 4, 5, 6} P(even)=P(2)+P(4)+P(6)=1/6+1/6=1/2

General Addition Rule ¨ For any two events A and B P(A∪B)=P(A)+P(B)–P(A∩B) A A∩B B

Example 6. 4 ¨ Draw a card from a deck. What is the probability of getting an ace or a spade? U P(ace or spade) =P(ace)+P(spade) – P(ace and spade) =4/52+13/52 – 1/52 =16/52

6. 5 Conditional Probability ¨ Roll a die. The probability of getting any number in the set of {1, 2, 3, 4, 5, 6} is 1/6 ! Try to predict the outcome when I roll the die. We predict that any number will have the same probability of showing up. ¨ How about if you know some prior information?

If you know the number is even ¨ Re-evaluate the probabilities: 0 probabilities for all 3 odd numbers equal probabilities for 3 even numbers (each even number has a probability of 1/3) This is called the conditional probability.

Notation: P(A|B) ¨ The conditional probability of event A, given event B (occurs) P(1|even)=P(3|even)=P(5|even)=0 P(2|even)=P(4|even)=P(6|even)=1/3

Conditional Probability ¨ S={1, 2, 3, 4, 5, 6} ¨ E=even ¨ L=less than or equal to 3 ¨ P(E|L) is the probability of “E given L”. ¨ P(even given that point total≤ 3) =P(E|L)=1/3. E L 4, 6, 2 1, 3 5

Conditional Probability ¨ Verify: P(1|even)=0 P(2|even)=1/3

Example 6. 5 ¨ Hair Eye Probability brown blue 0. 3 brown 0. 4 blond blue 0. 2 blond brown 0. 1 ----------------------P(blue eyes|blond hair) =P(blue eyes and blond hair)/P(blond hair) =0. 2/(0. 2+0. 1)=2/3=0. 67 P(blond hair|blue eyes) = P(blond hair and blue eyes)/P(blue eyes) =0. 2/(0. 3+0. 2)=2/5=0. 40

A simpler way: tabulate the probabilities Hair brown blond Subtotal Eye blue 0. 3 0. 2 0. 5 brown 0. 4 0. 1 0. 5 Subtotal 0. 7 0. 3 1. 0 P(blue eyes|blond hair) =0. 2/0. 3

Exercise ¨ Candidates for a committee of 3 people include 6 women and 4 men. What is the probability that the # of women chosen is 2?

Exercise ¨ Sometimes a laboratory assistant has lunch at the cafeteria where she works, sometimes she brings her own lunch, sometimes she has lunch at a nearby restaurant, sometimes she goes home for lunch, and sometimes she skips lunch to lose weight. If the corresponding probabilities are 0. 23, 0. 31, 0. 15, 0. 24 and 0. 07, find the probabilities that she will – – Have lunch at the cafeteria or the nearby restaurant; Bring her own lunch, go home for lunch, or skip lunch altogether; Have lunch at the cafeteria or go home for lunch; Not skip lunch to lose weight.

Exercise ¨ The probability that it will rain in Tucson, Arizona, on a day in mid-August, that there will be a thunderstorm on that day, and that there will be rain as well as a thunderstorm are 0. 27, 0. 24 and 0. 15. What is the probability that there will be rain and /or a thunderstorm in Tucson on such a day?

Exercise ¨ Roll a die. What is the probability of getting a number less than 5 if we know that it is an even number?

Exercise ¨ The probability that Henry will like a new movie is 0. 70 and the probability that Jane, his girlfriend, will like it is 0. 60. If the probability is 0. 28 that he will like it and she will dislike it, what is the probability that he will like it given that she is not going to like it?

6. 6 Multiplication Rules ¨ Conditional probability formula ¨ This is equivalent to P(A∩B)=P(A|B)P(B) Similarly P(A∩B)=P(B|A)P(A)

Example 6. 6 Pick up two cards from a deck without replacement What is the probability of getting two aces?

Method 1: like in Example 5. 13

Method 2 ¨ A=first card is an ace ¨ B=second card is an ace P(A)=4/52 P(B|A)=3/51

¨ Toss 2 dice ¨ A= 6 first die ¨ B= 6 second die

For more than 2 events multiply conditional probabilities in a similar way ¨ P(A∩B∩C)=P(A)P(B|A)P(C|A∩B )

Example 6. 7 ¨ Pick up 3 cards without replacement. Find the probability of getting 3 aces. A=1 st card is an ace; B=2 nd card is an ace; C=3 rd card is an ace. P(A)=4/52 P(B|A)=3/51 P(C|A∩B)=2/50 P(A∩B∩C)=(4/52)(3/51)(2/50)

Example 6. 8 ¨ Probability of getting 4 aces in 4 cards

Independent events vs Dependent events ¨ Roll a red die and white die. A=red is a 6; B= white is a 6 Then P(A)=P(B)=1/6; P(A∩B)=1/36; P(B|A)=P(A∩B )/P(A)=1/6 =P(B) P(white is 6|red is 6) = P(white is 6) The probability that white is a 6 is independent of whether red is a 6. “red is a 6” and “white is 6” are independent events.

Independence If the conditional probability of B given A is equal to the unconditional probability of B P(B|A)=P(B) then, A and B are said to be independent This is equivalent to P(A|B)=P(A) Or P(A∩B )=P(B)P(A|B)=P(B)*P(A) O. W. , A and B are independent

For independent events A and B P(A∩B )=P(A)*P(B) P(A|B)=P(A) P(B|A)=P(B) If any of these 3 conditions holds, then A & B are independent. If any of these 3 conditions does not hold, then A & B are dependent.

Example 6. 9 ¨ Flip two fair coins. Probability of getting two heads? Method 1: Sample space: {HH, HT, TH, TT} P(HH)=1/4 Method 2: A=head on 1 st flip={HH, HT} B=head on 2 nd flip={HH, TH} Show P(B|A)=P(B) P(HH)=P(A∩B)=P(A)P(B)=(1/2)=1/4

Example 6. 10 ¨ Pick a card, set H=heart A=ace K=king P(H)=13/52=1/4 P(H|K)=1/4 H and K are independent P(A)=4/52 P(A|K)=0 A and K are dependent

Independent and mutually exclusive ¨ They are totally different concepts! Do not mix these up. ¨ Difference?

How to get the probability? ¨ The solutions of most probability problems use the following facts. ¨ For equally likely outcomes #of outcomes in A P(A)=—————— total # of possible outcomes ¨ P(not A)=1–P(A)

More ¨ For mutually exclusive events P(A 1 or A 2 or … or Ak)= P(A 1)+P(A 2)+… P(Ak) ¨ For any two events P(A or B)=P(A∪B)=P(A)+P(B)–P(A∩B) ¨ P(A|B)=P(A∩ B)/P(B)

More ¨ P(A and B)=P(A∩B)=P(A)P(B|A) or P(B)P(A|B) ¨ For independent events P(A|B)=P(A); P(B|A)=P(B); P(A∩B)=P(A)P(B) ¨ For independent events A 1, A 2, …, Ak P(A 1∩ A 2 ∩ …∩ Ak)=P(A 1)…P(Ak)

More ¨ For any events P(A 1∩ A 2 ∩ …∩ Ak) =P(A 1)P(A 2|A 1)…P(Ak|A 1∩…∩Ak-1)

Example 6. 11 Toss a coin 3 times. Find P(2 heads)=? HHT (½)(½)(½)=1/8 HTH (½)(½)(½)=1/8 THH (½)(½)(½)=1/8 P(2 heads)=P(HHT∪HTH∪THH)=P(HHT)+P(HTH)+P(THH)=3/8 P(at least one head)=? =1–P(no head)=1–P(TTT) =1 -1/2*1/2 =1 -1/8 =7/8

Example 6. 12 Pick 5 cards P(2 aces|1 king)= P(2 aces and 1 king)/P(1 king) #of ways to pick up 2 aces and 1 king #of ways to pick up 1 king

Example 6. 13 ¨ Deal 5 cards. What is the probability that you get 5 face cards? (J, Q, or K) Method 1: Method 2: multiply conditional probability

Example 6. 14 ¨ Deal 5 cards, what is the probability of getting 4 aces?

Exercise ¨ Suppose that the probability is 0. 45 that a rare tropical disease is diagnosed correctly and, if diagnosed correctly, the probability is 0. 60 that the patient will be cured. What is the probability that a person who has the disease will be diagnosed correctly and cured?

Exercise ¨ The probability that Henry will like a new movie is 0. 70 and the probability that Jane, his girlfriend, will like it is 0. 60. If the probability is 0. 28 that he will like it and she will dislike it, what is the probability that he will like it given that she is not going to like it? ¨ Are the two events (Henry likes the movie and Jane likes it) independent?

6. 7 Bayes Theorem ¨ A test for cancer has the following properties: C = a patient has cancer + = test is positive, claiming patient has cancer P(C)=0. 001 P(+|C) =0. 98 P(+|C’)= 0. 01 Question 1: what % of patients test positive?
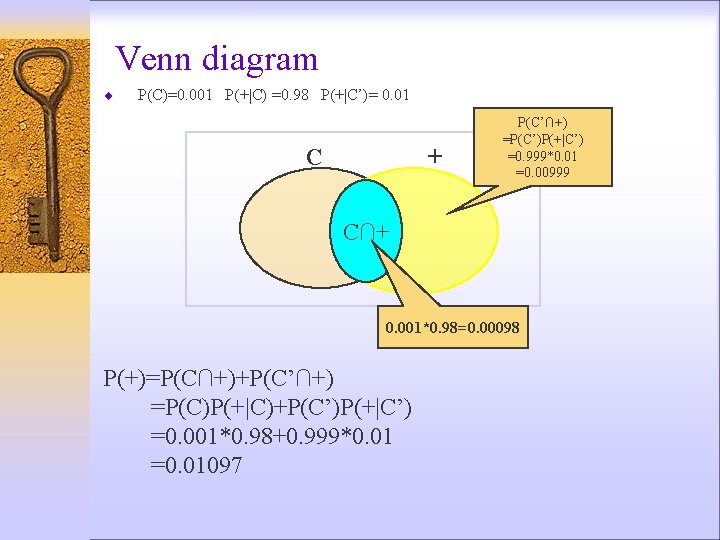
Venn diagram ¨ P(C)=0. 001 P(+|C) =0. 98 P(+|C’)= 0. 01 C + P(C’∩+) =P(C’)P(+|C’) =0. 999*0. 01 =0. 00999 C∩+ 0. 001*0. 98=0. 00098 P(+)=P(C∩+)+P(C’∩+) =P(C)P(+|C)+P(C’)P(+|C’) =0. 001*0. 98+0. 999*0. 01 =0. 01097
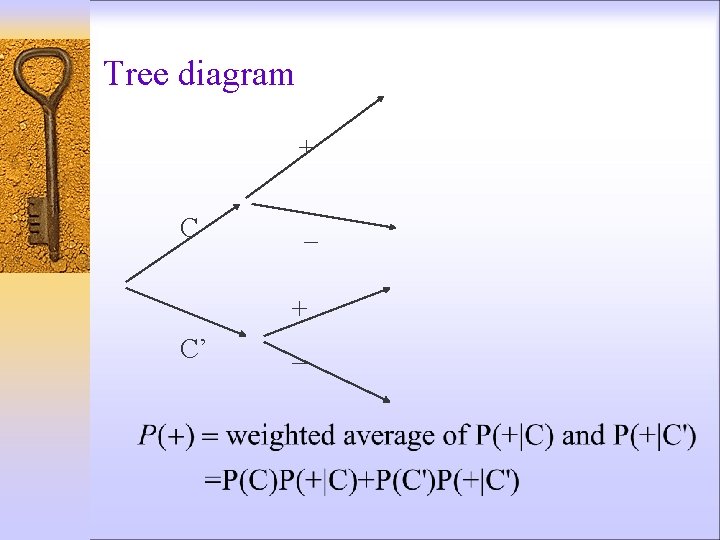
Tree diagram + C C’ _ + _

Q 2: What is the probability a patient has cancer given that patient tests positive? P(C∩+) 0. 00098 ———— =0. 089 P(+) 0. 01097 Most of + cases are from C’ !!! A tree diagram helps!

Rule of total probability P(A)=P(B)P(A|B)+P(B')P(A|B') Weighted average of P(A|B) & P(A|B’) P(B)P(A|B) A P(A|B) B P( B) B’ P( B’) A P(B')P(A|B') P(A|B’) Generalization: B 1, B 2, B 3 Use this formula when Given: P(A|B) P(A|B’) Need: P(A) P(B)

Bayes’ Theorem Use this when Given: P(A|B) P(A|B’) Need: P(B|A) P(B)

Example: Insurance Company figures A=accident in a year AP=accident prone Given: P(A|AP)=0. 10 P(A|AP’)=0. 05 P(AP)=0. 2 Find P(A) Find P(AP|A)

Bayes’ Theorem If B 1, B 2, …, and Bk are mutually excusive events of which one must occur, then

Exercise ¨ In a cannery, assembly lines I, II, and III account for 50%, 30%, and 20% of total output. If 0. 4% of the cans from assembly line I are improperly sealed, and the corresponding percentages for assembly lines II and III are 0. 6% and 1. 2%. Q 1: Probability of a can being improperly sealed. Q 2: Probability of a can being sealed from line I if it is found to be improperly sealed
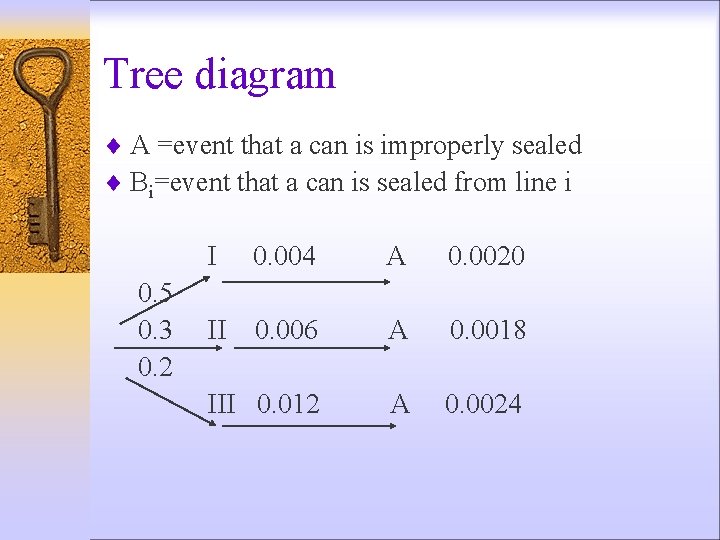
Tree diagram ¨ A =event that a can is improperly sealed ¨ Bi=event that a can is sealed from line i I 0. 5 0. 3 0. 2 0. 004 A 0. 0020 II 0. 006 A 0. 0018 III 0. 012 A 0. 0024

Solutions: ¨ Answer #1: ¨ Answer #2:

Exercise ¨ Imagine that the probability is 0. 95 that a certain test will correctly diagnose a person with diabetes as being diabetic, and that it is 0. 05 that the test will incorrectly diagnose a person without diabetes as being diabetic. Given that roughly 10% of the population is diabetic, what is the probability that a person diagnosed as being diabetic actually has diabetes?

Homework on 6. 7 (not to be turned in) 6. 70*, 6. 71*, 6. 72*, 6. 73*, 6. 78 For the problems marked *, write down what is given and what you need to find in symbolic notation.
- Slides: 70