CHAPTER 6 Risk Aversion and Capital Allocation to










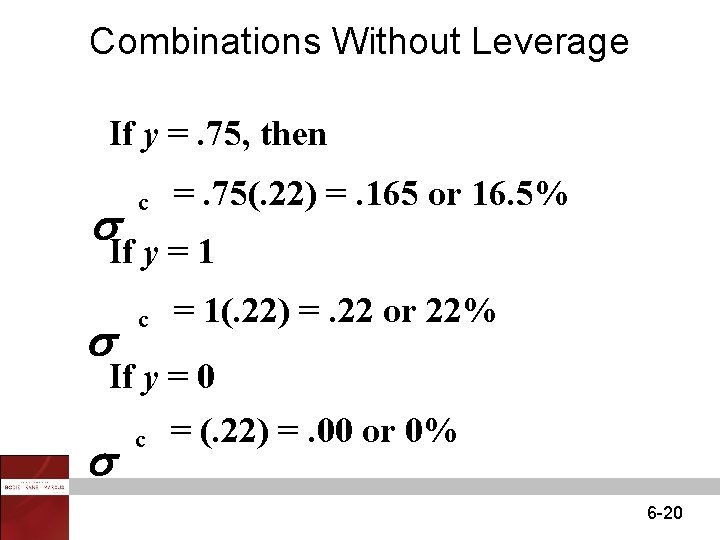





- Slides: 33

CHAPTER 6 Risk Aversion and Capital Allocation to Risky Assets Investments, 8 th edition Bodie, Kane and Marcus Slides by Susan Hine Mc. Graw-Hill/Irwin Copyright © 2009 by The Mc. Graw-Hill Companies, Inc. All rights reserved.

Risk and Risk Aversion • Speculation – Considerable risk • Sufficient to affect the decision – Commensurate gain • Gamble – Bet or wager on an uncertain outcome 6 -2

Risk Aversion and Utility Values • Risk averse investors reject investment portfolios that are fair games or worse • These investors are willing to consider only risk-free or speculative prospects with positive risk premiums • Intuitively one would rank those portfolios as more attractive with higher expected returns 6 -3

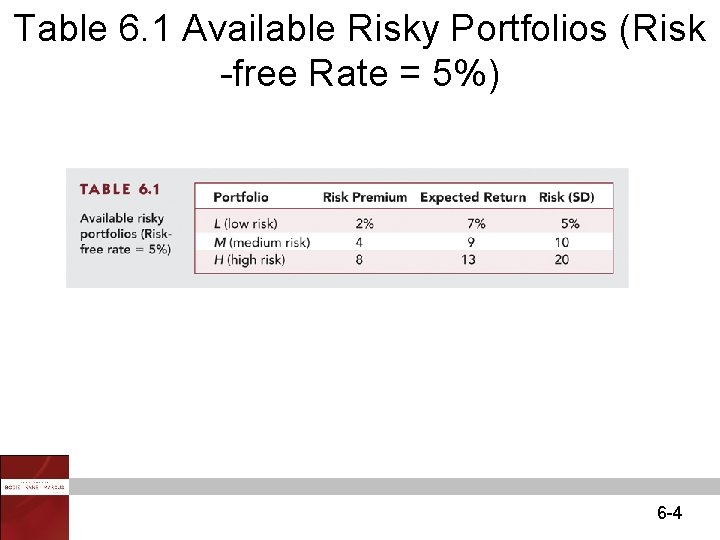
Table 6. 1 Available Risky Portfolios (Risk -free Rate = 5%) 6 -4

Utility Function Where U = utility E ( r ) = expected return on the asset or portfolio A = coefficient of risk aversion s 2 = variance of returns 6 -5

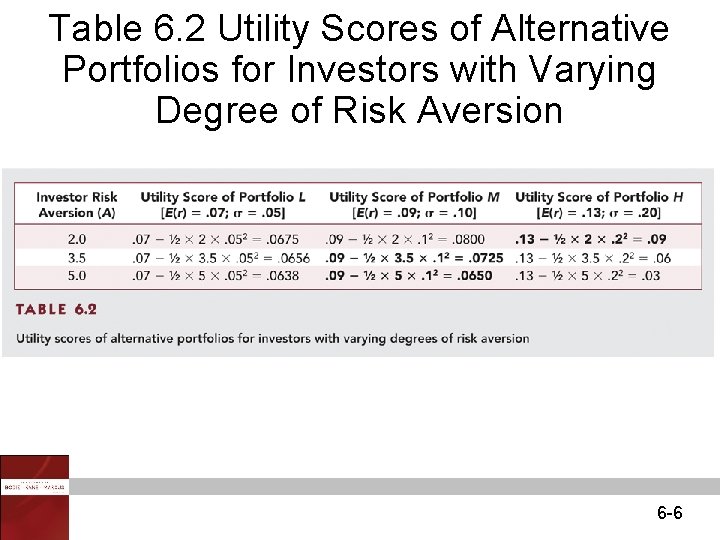
Table 6. 2 Utility Scores of Alternative Portfolios for Investors with Varying Degree of Risk Aversion 6 -6

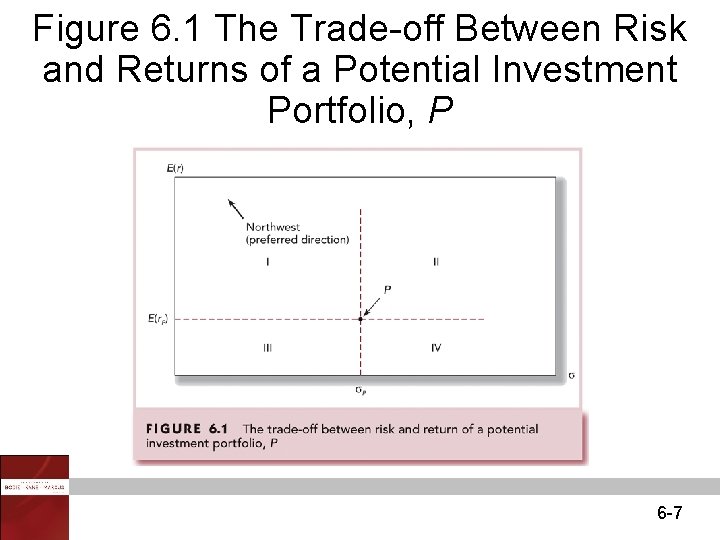
Figure 6. 1 The Trade-off Between Risk and Returns of a Potential Investment Portfolio, P 6 -7

Estimating Risk Aversion • Observe individuals’ decisions when confronted with risk • Observe how much people are willing to pay to avoid risk – Insurance against large losses 6 -8

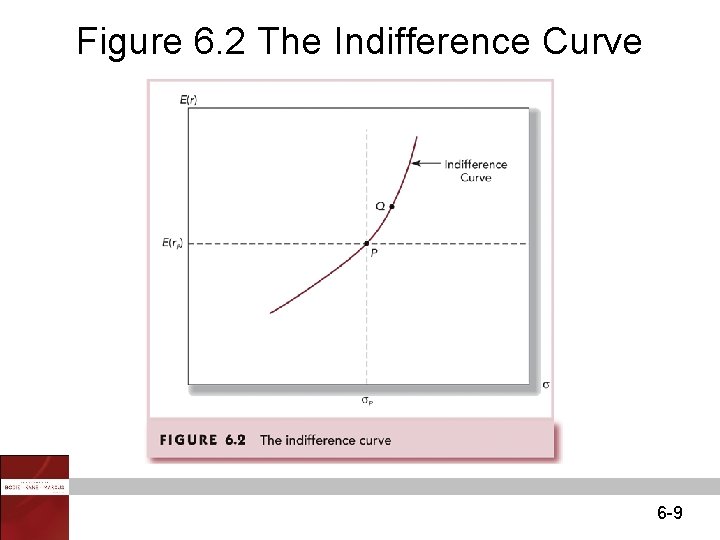
Figure 6. 2 The Indifference Curve 6 -9

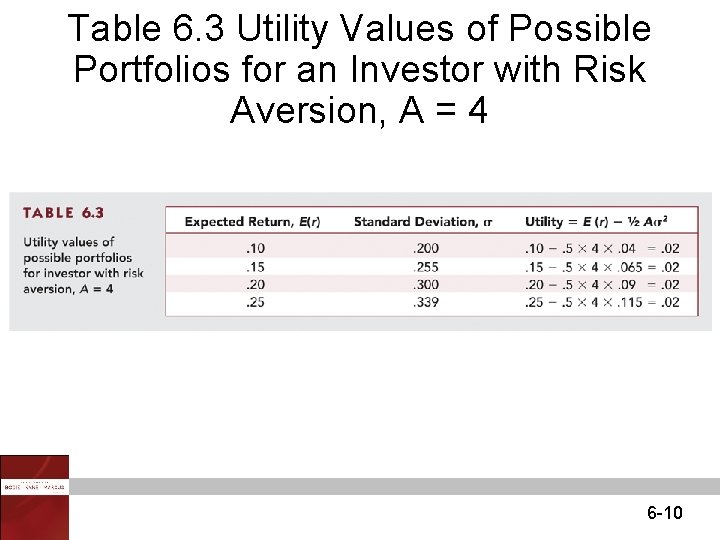
Table 6. 3 Utility Values of Possible Portfolios for an Investor with Risk Aversion, A = 4 6 -10

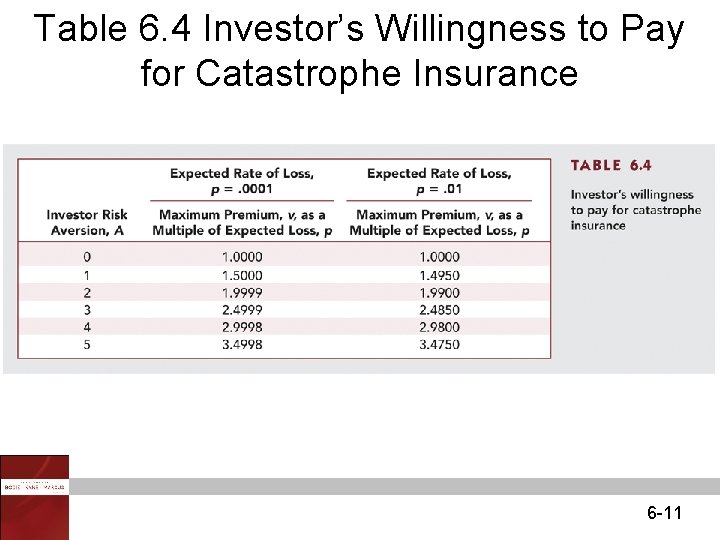
Table 6. 4 Investor’s Willingness to Pay for Catastrophe Insurance 6 -11

Capital Allocation Across Risky and Risk. Free Portfolios • Control risk – Asset allocation choice • Fraction of the portfolio invested in Treasury bills or other safe money market securities 6 -12

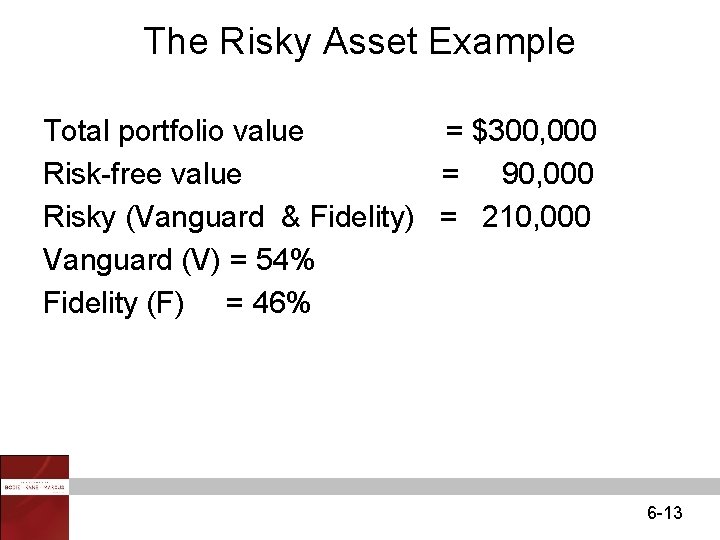
The Risky Asset Example Total portfolio value = $300, 000 Risk-free value = 90, 000 Risky (Vanguard & Fidelity) = 210, 000 Vanguard (V) = 54% Fidelity (F) = 46% 6 -13

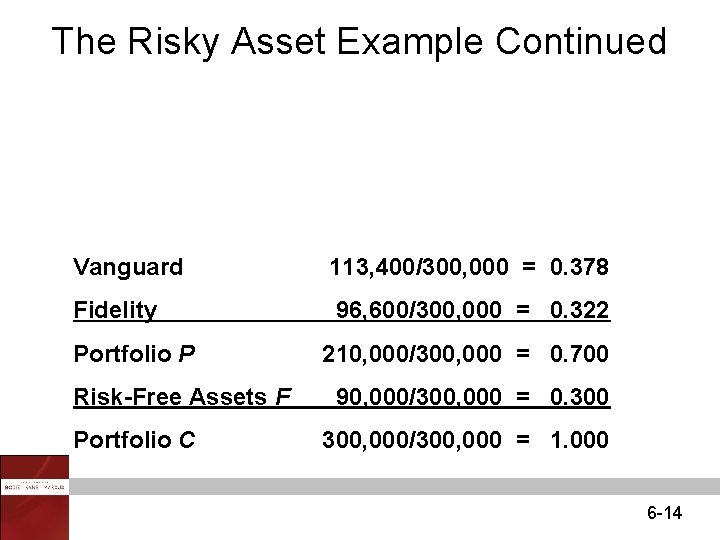
The Risky Asset Example Continued Vanguard 113, 400/300, 000 = 0. 378 Fidelity 96, 600/300, 000 = 0. 322 Portfolio P Risk-Free Assets F Portfolio C 210, 000/300, 000 = 0. 700 90, 000/300, 000 = 0. 300, 000/300, 000 = 1. 000 6 -14

The Risk-Free Asset • Only the government can issue default-free bonds – Guaranteed real rate only if the duration of the bond is identical to the investor’s desire holding period • T-bills viewed as the risk-free asset – Less sensitive to interest rate fluctuations 6 -15

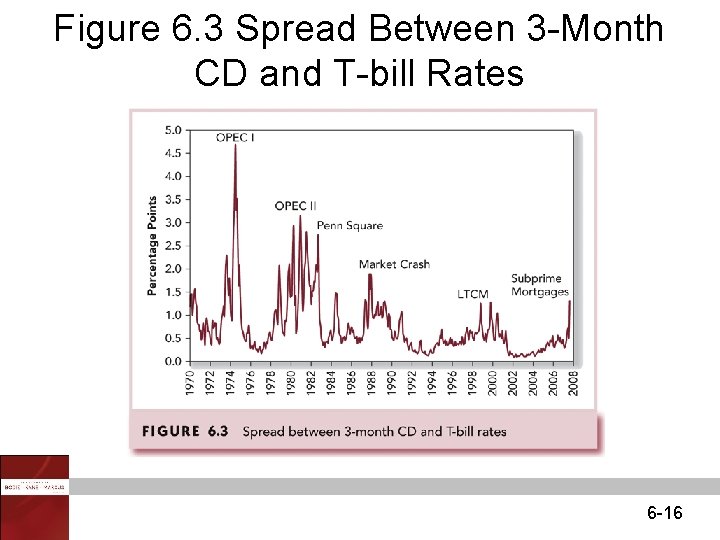
Figure 6. 3 Spread Between 3 -Month CD and T-bill Rates 6 -16

Portfolios of One Risky Asset and a Risk. Free Asset • It’s possible to split investment funds between safe and risky assets. • Risk free asset: proxy; T-bills • Risky asset: stock (or a portfolio) 6 -17

Example Using Chapter 6. 4 Numbers rf = 7% rf = 0% E(rp) = 15% p = 22% y = % in p (1 -y) = % in rf 6 -18

Expected Returns for Combinations rc = complete or combined portfolio For example, y =. 75 E(rc) =. 75(. 15) +. 25(. 07) =. 13 or 13% 6 -19
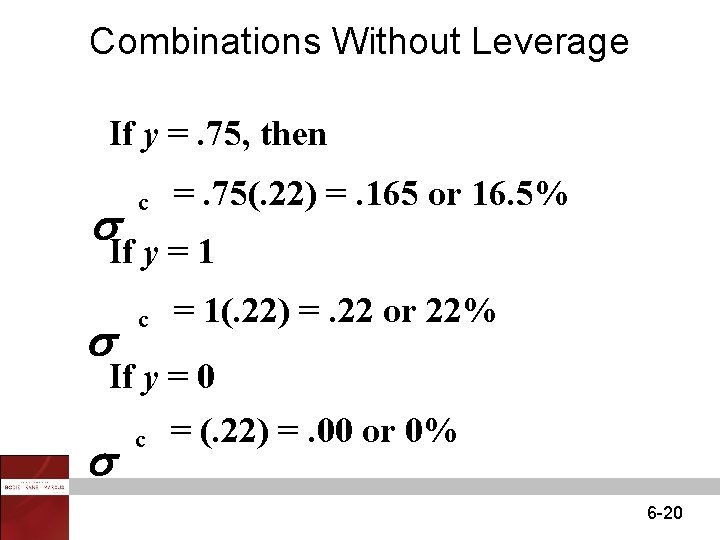
Combinations Without Leverage If y =. 75, then c c =. 75(. 22) =. 165 or 16. 5% If y = 1(. 22) =. 22 or 22% If y = 0 c = (. 22) =. 00 or 0% 6 -20

Capital Allocation Line with Leverage Borrow at the Risk-Free Rate and invest in stock. Using 50% Leverage, rc = (-. 5) (. 07) + (1. 5) (. 15) =. 19 c = (1. 5) (. 22) =. 33 6 -21

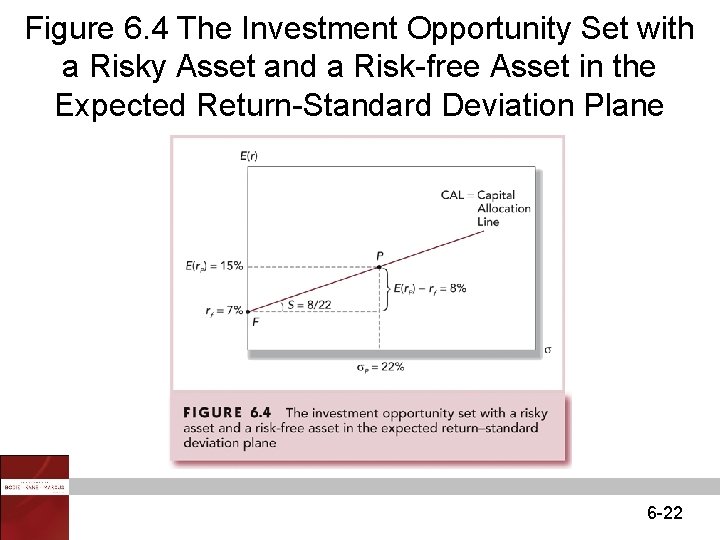
Figure 6. 4 The Investment Opportunity Set with a Risky Asset and a Risk-free Asset in the Expected Return-Standard Deviation Plane 6 -22

Figure 6. 5 The Opportunity Set with Differential Borrowing and Lending Rates 6 -23

Risk Tolerance and Asset Allocation • The investor must choose one optimal portfolio, C, from the set of feasible choices – Trade-off between risk and return – Expected return of the complete portfolio is given by: – Variance is: 6 -24

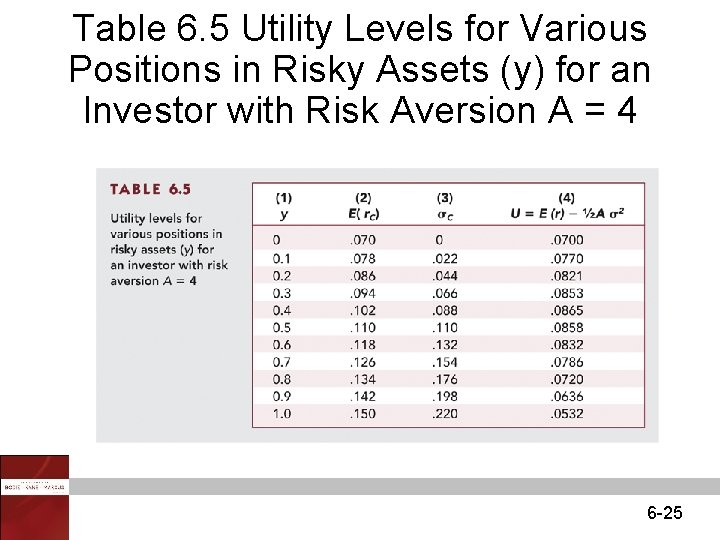
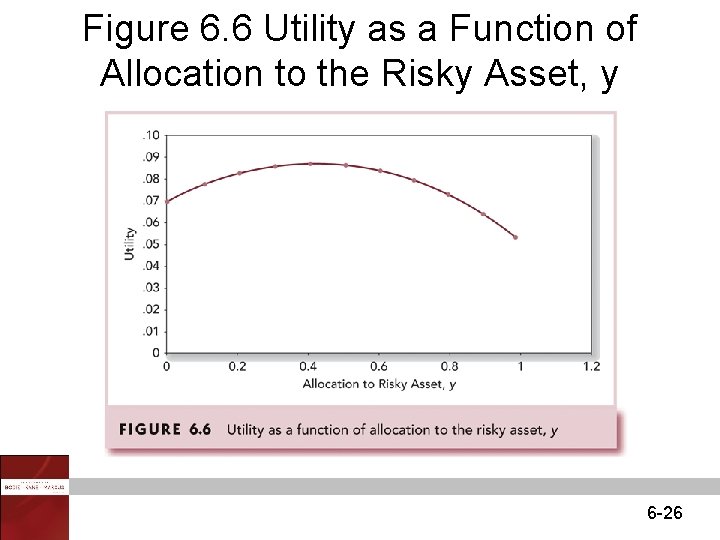
Table 6. 5 Utility Levels for Various Positions in Risky Assets (y) for an Investor with Risk Aversion A = 4 6 -25

Figure 6. 6 Utility as a Function of Allocation to the Risky Asset, y 6 -26

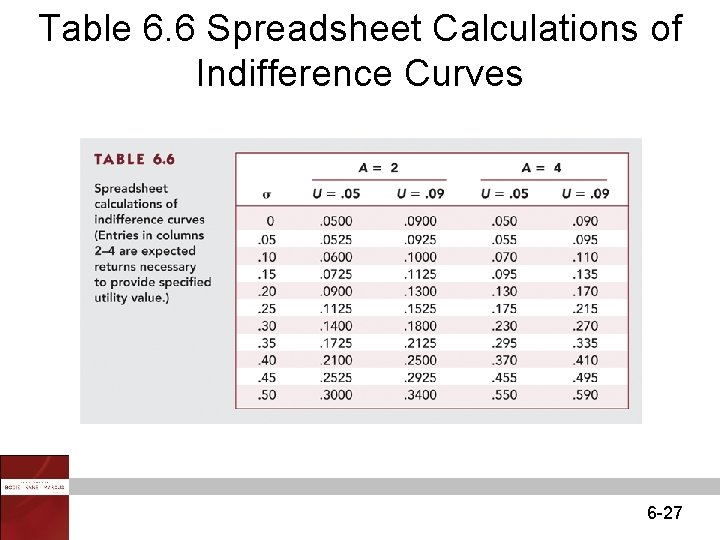
Table 6. 6 Spreadsheet Calculations of Indifference Curves 6 -27

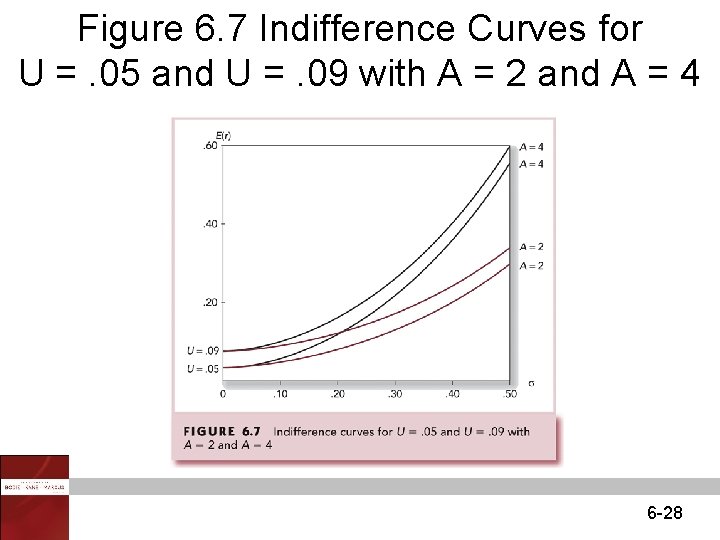
Figure 6. 7 Indifference Curves for U =. 05 and U =. 09 with A = 2 and A = 4 6 -28

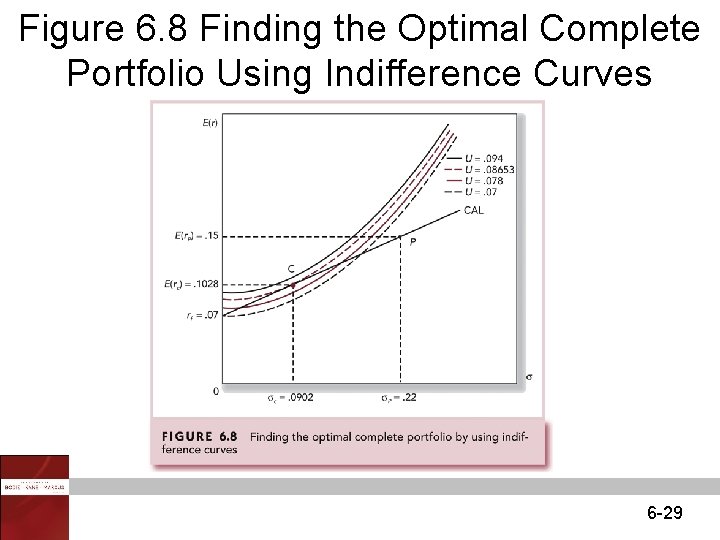
Figure 6. 8 Finding the Optimal Complete Portfolio Using Indifference Curves 6 -29

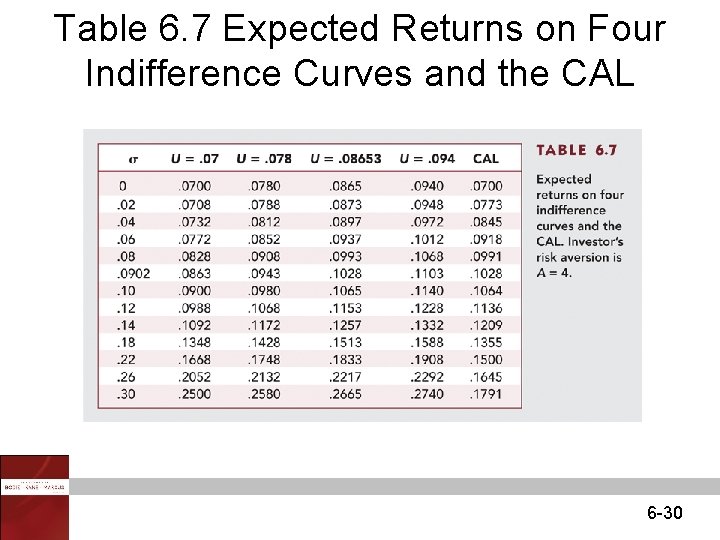
Table 6. 7 Expected Returns on Four Indifference Curves and the CAL 6 -30

Passive Strategies: The Capital Market Line • Passive strategy involves a decision that avoids any direct or indirect security analysis • Supply and demand forces may make such a strategy a reasonable choice for many investors 6 -31

Passive Strategies: The Capital Market Line Continued • A natural candidate for a passively held risky asset would be a well-diversified portfolio of common stocks • Because a passive strategy requires devoting no resources to acquiring information on any individual stock or group we must follow a “neutral” diversification strategy 6 -32

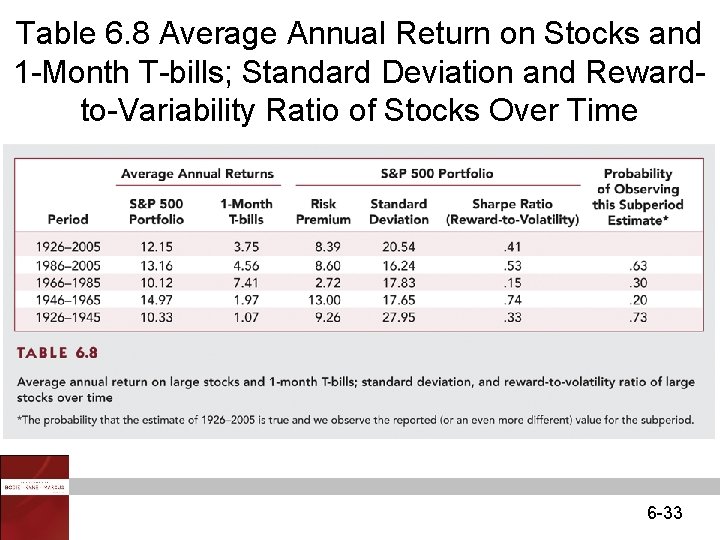
Table 6. 8 Average Annual Return on Stocks and 1 -Month T-bills; Standard Deviation and Rewardto-Variability Ratio of Stocks Over Time 6 -33