Chapter 6 Probability Distributions Probability Distribution Describes possible

Chapter 6 Probability Distributions

Probability Distribution • Describes possible numerical outcomes of a chance process

Probability Distribution • Describes possible numerical outcomes of a chance process • Allows you to find probability of any set of possible outcomes
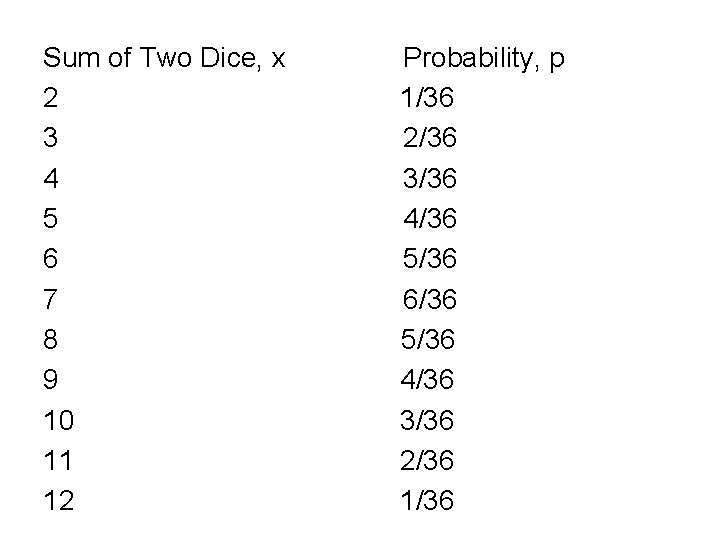
Sum of Two Dice, x 2 3 4 5 6 7 8 9 10 11 12 Probability, p 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36

Section 6. 1 Random Variables and Expected Value

Sampling and Probability Connection between these?

Sampling and Probability Connection between these? Sampling: Estimates a parameter (characteristic) of a population by selecting data (taking random sample) from that population

Sampling and Probability Sampling: Estimates a parameter (characteristic) of a population by selecting data (taking random sample) from that population Probability: Deals with chance of getting a specified outcome in a sample when you know about the population

Important Statistical Question What might an unknown population look like?

Important Statistical Question What might an unknown population look like? Why not conduct a census to determine this?

Important Statistical Question What might an unknown population look like? Why not conduct a census to determine this? • May be impossible or impractical – Cost too much – Take too much time – Destructive data collection

What might an unknown population look like? 1) Use probability to learn what samples from known populations tend to look like

What might an unknown population look like? 1) Use probability to learn what samples from known populations tend to look like

What might an unknown population look like? 1) Use probability to learn what samples from known populations tend to look like 2) Take sample from unknown population & compare results to samples from known populations

What might an unknown population look like? 3) Populations which your sample appears to fit right in are the plausible homes for your sample
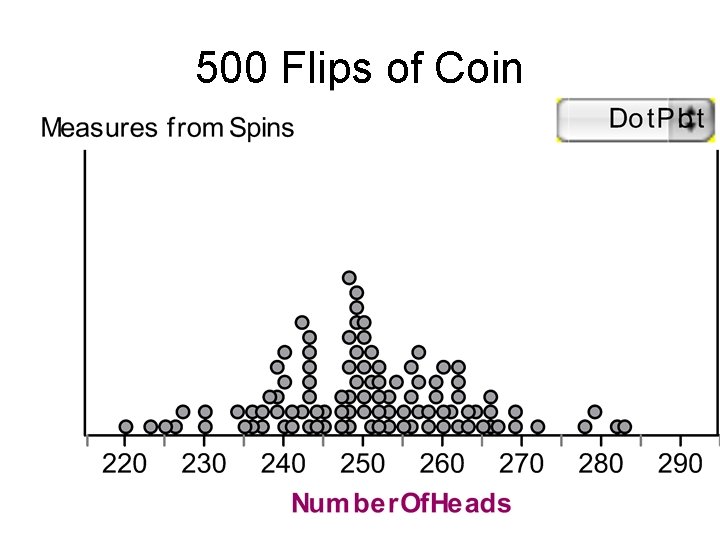
500 Flips of Coin

Probability Distributions Probability distributions mainly result from two different ways: 1) through data collection

Probability Distributions Probability distributions mainly result from two different ways: 1) through data collection 2) through theory

Probability Distributions from Data Suppose you are working for a contractor who is building 500 new single-family houses. Your boss wants to know how many parking spaces will be needed per house.

Probability Distributions from Data Suppose you are working for a contractor who is building 500 new single-family houses. Your boss wants to know how many parking spaces will be needed per house. What might happen if too few parking spaces are provided? Too many?

Probability Distributions from Data Suppose you are working for a contractor who is building 500 new single-family houses. Your boss wants to know how many parking spaces will be needed per house. So how do you proceed?

Probability Distributions from Data One method is to take a random sample of 500 households to estimate number of vehicles per household

Probability Distributions from Data One method is to take a random sample of 500 households to estimate number of vehicles per household -- takes time and money for this

Probability Distributions from Data Second method is to search for existing data that you can reasonably assume represent your situation

Probability Distributions from Data Second method is to search for existing data that you can reasonably assume represent your situation • Need reliable source of data – Not Wikipedia
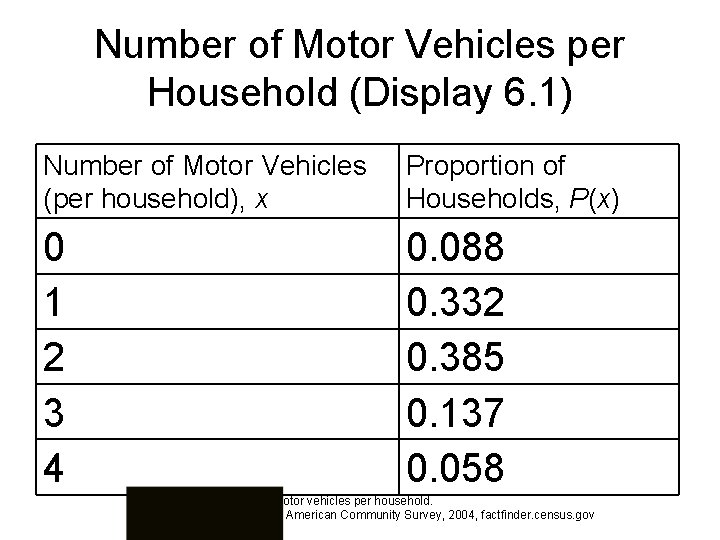
Number of Motor Vehicles per Household (Display 6. 1) Number of Motor Vehicles (per household), x Proportion of Households, P(x) 0 1 2 3 4 0. 088 0. 332 0. 385 0. 137 0. 058 Display 6. 1: The number of motor vehicles per household. Source: U. S. Census Bureau, American Community Survey, 2004, factfinder. census. gov
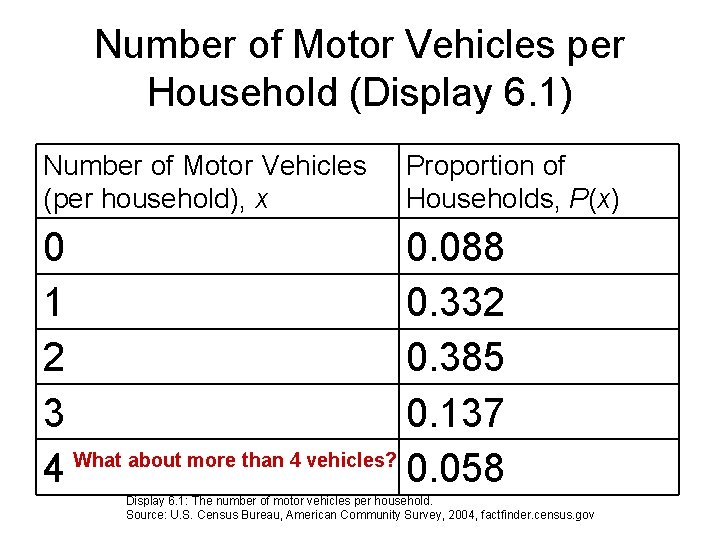
Number of Motor Vehicles per Household (Display 6. 1) Number of Motor Vehicles (per household), x Proportion of Households, P(x) 0 0. 088 1 0. 332 2 0. 385 3 0. 137 What about more than 4 vehicles? 4 0. 058 Display 6. 1: The number of motor vehicles per household. Source: U. S. Census Bureau, American Community Survey, 2004, factfinder. census. gov
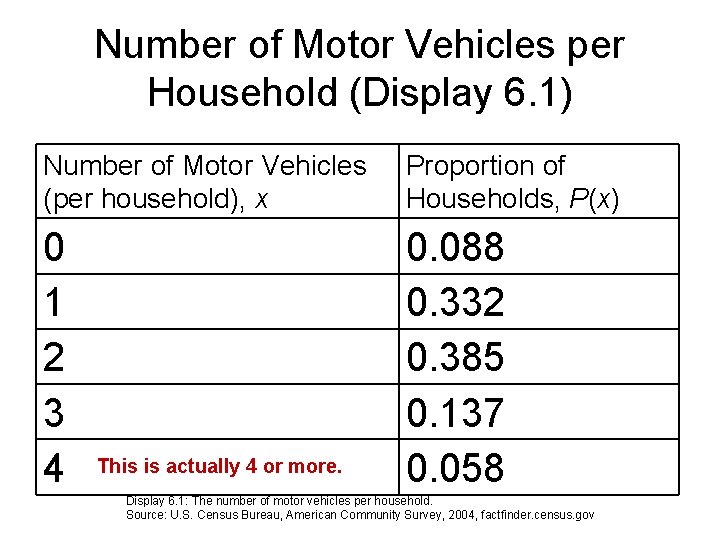
Number of Motor Vehicles per Household (Display 6. 1) Number of Motor Vehicles (per household), x Proportion of Households, P(x) 0 1 2 3 4 0. 088 0. 332 0. 385 0. 137 0. 058 This is actually 4 or more. Display 6. 1: The number of motor vehicles per household. Source: U. S. Census Bureau, American Community Survey, 2004, factfinder. census. gov
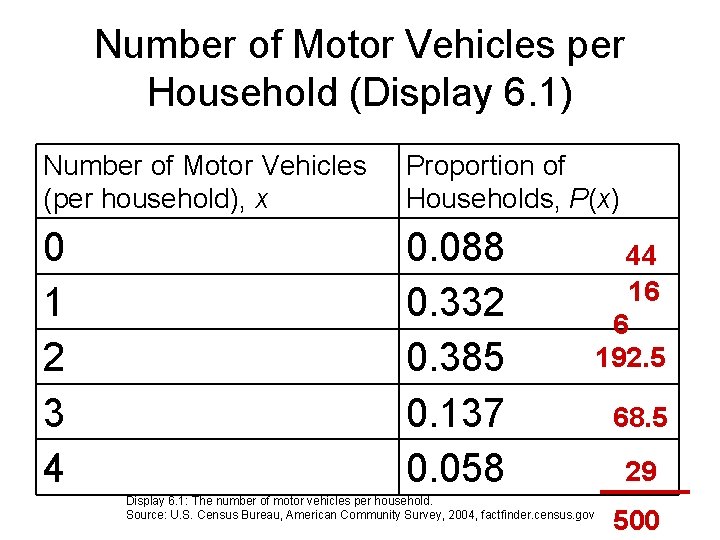
Number of Motor Vehicles per Household (Display 6. 1) Number of Motor Vehicles (per household), x Proportion of Households, P(x) 0 1 2 3 4 0. 088 0. 332 0. 385 0. 137 0. 058 Display 6. 1: The number of motor vehicles per household. Source: U. S. Census Bureau, American Community Survey, 2004, factfinder. census. gov 44 16 6 192. 5 68. 5 29 500

Good News & Bad News Your boss is so pleased with your work, he gives you a bonus!

Good News & Bad News Your boss is so pleased with your work, he gives you a bonus! Alas, he now knows you are a skilled statistician so you get a new project.

New Project 500 duplexes are also being built, so your boss wants to know something about the number of vehicles that will be parked by the two households occupying a duplex. What do you do?

Way Ahead You can take two households at random from the distribution in Display 6. 1 and add their numbers.

Way Ahead You can take two households at random from the distribution in Display 6. 1 and add their numbers. If you replicate this 500 times, you’ll have an approximation of the distribution your boss wants concerning duplex parking.

Way Ahead As typical for all modeling problems, accuracy of result depends on appropriateness of model used. What assumptions do you make?

Assumptions 1) Households living in duplexes mirror households in general with respect to vehicles per household

Assumptions 1) Households living in duplexes mirror households in general with respect to vehicles per household 2) Number of vehicles in one household is independent of the number of vehicles in the neighboring household How do you proceed selecting two households at random to represent a duplex?

Assigning Random Digits Number of Motor Vehicles (per household), x Proportion of Households, P(x) 0 1 2 3 4 0. 088 0. 332 0. 385 0. 137 0. 058 Display 6. 1: The number of motor vehicles per household. Source: U. S. Census Bureau, American Community Survey, 2004, factfinder. census. gov

Assigning Random Digits Number of Motor Vehicles (per household), x Proportion of Households, P(x) 0 1 2 3 4 0. 088 0. 332 0. 385 0. 137 0. 058 001 - 088 Display 6. 1: The number of motor vehicles per household. Source: U. S. Census Bureau, American Community Survey, 2004, factfinder. census. gov
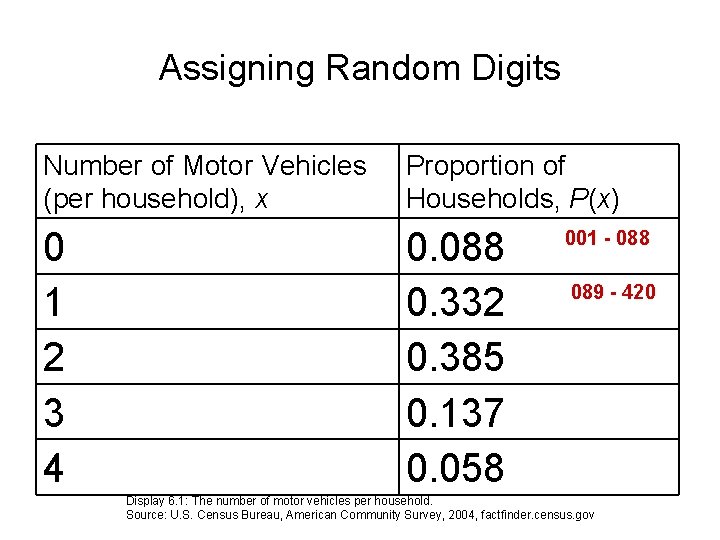
Assigning Random Digits Number of Motor Vehicles (per household), x Proportion of Households, P(x) 0 1 2 3 4 0. 088 0. 332 0. 385 0. 137 0. 058 001 - 088 089 - 420 Display 6. 1: The number of motor vehicles per household. Source: U. S. Census Bureau, American Community Survey, 2004, factfinder. census. gov
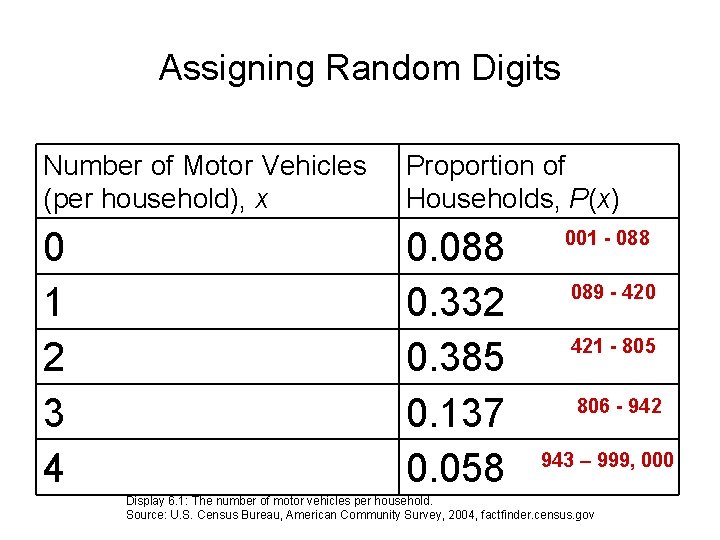
Assigning Random Digits Number of Motor Vehicles (per household), x Proportion of Households, P(x) 0 1 2 3 4 0. 088 0. 332 0. 385 0. 137 0. 058 001 - 088 089 - 420 421 - 805 806 - 942 943 – 999, 000 Display 6. 1: The number of motor vehicles per household. Source: U. S. Census Bureau, American Community Survey, 2004, factfinder. census. gov
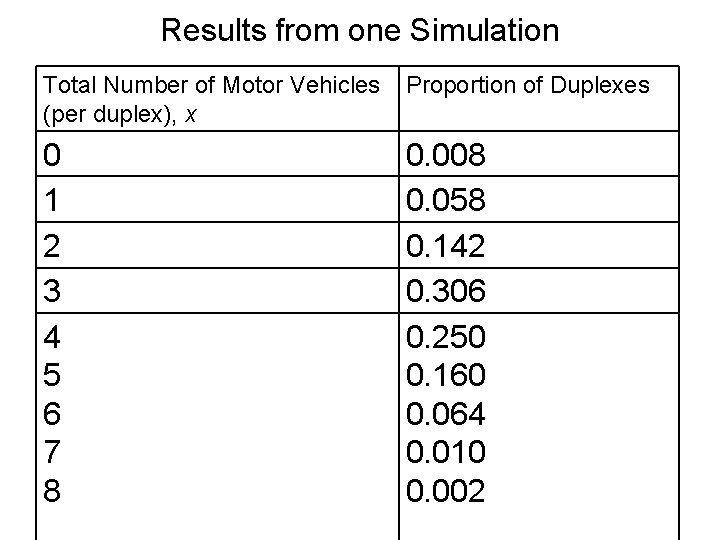
Results from one Simulation Total Number of Motor Vehicles (per duplex), x Proportion of Duplexes 0 1 2 3 4 5 6 7 8 0. 008 0. 058 0. 142 0. 306 0. 250 0. 160 0. 064 0. 010 0. 002

Question When you sample from distributions like the one in Display 6. 1 using random digits, why should repeated random digits be used again rather than discarded?

A triple of random digits doesn’t represent an individual household but, along with other triples in its category, represents the many households in its category.

Probability Distributions from Data You now have two ways to establish probability distributions from data:

Probability Distributions from Data You now have two ways to establish probability distributions from data: 1) Use relative frequencies from data already collected to study a future random variable

Probability Distributions from Data You now have two ways to establish probability distributions from data: 1) Use relative frequencies from data already collected to study a future random variable 2) Use simulation to build approximate probability distribution

Probability Distribution from Theory Use rules of theoretical probability to build a probability distribution from basic principles and assumptions

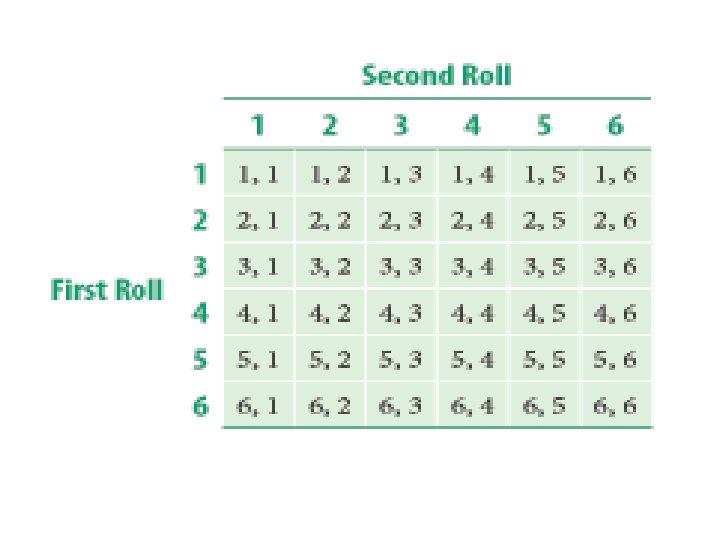
Rolling Two Dice 1) What is the total number of possible outcomes when you roll a pair of dice?

Rolling Two Dice 1) What is the total number of possible outcomes when you roll a pair of dice? 36 2) How do you know this?

Rolling Two Dice 1) What is the total number of possible outcomes when you roll a pair of dice? 36 2) How do you know this? Fundamental Principle of Counting (multiply outcomes of each stage)

Construct Probability Distributions Construct two probability distributions: (1) sum of the two dice, (2) larger number of the two dice (in case of doubles, the larger and smaller number are the same).
Construct Probability Distributions

Sum of Two Dice, x 2 3 4 5 6 7 8 9 10 11 12 Probability, p
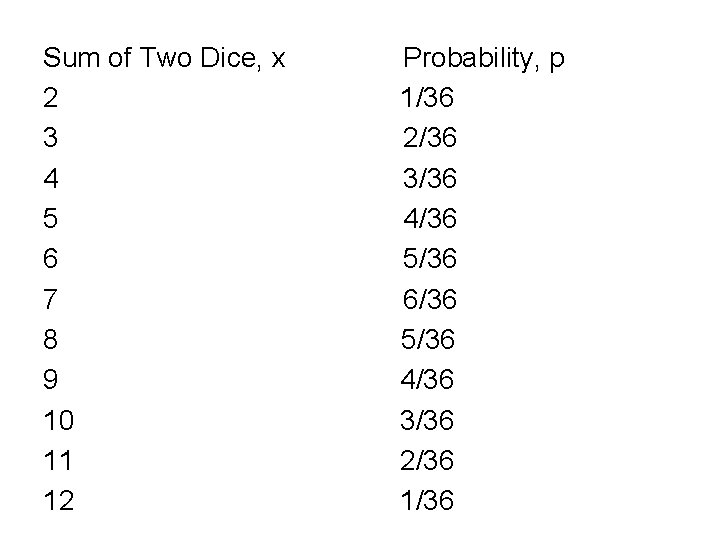
Sum of Two Dice, x 2 3 4 5 6 7 8 9 10 11 12 Probability, p 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36

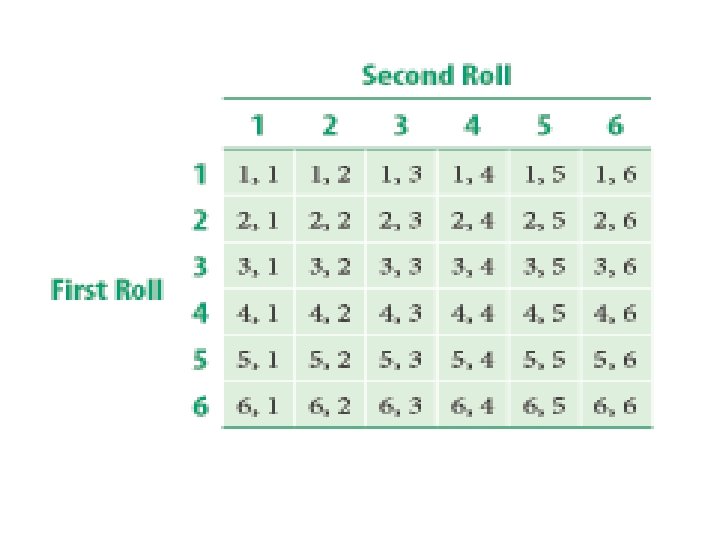
Larger Number Probability Distribution Larger Number, x Probability, p

Larger Number, x 1 2 3 4 5 6 Probability, p

Larger Number, x 1 2 3 4 5 6 Probability, p 1/36
Construct Probability Distributions

Larger Number, x 1 2 3 4 5 6 Total Probability, p 1/36 3/36 5/36 7/36 9/36 11/36 1

Sampling Lung Cancer Patients Suppose two lung cancer patients are randomly selected from the large population of people with that disease. Construct the probability distribution of X, the number of patients with lung cancer caused by smoking.

Sampling Lung Cancer Patients Suppose two lung cancer patients are randomly selected from the large population of people with that disease. Construct the probability distribution of X, the number of patients with lung cancer caused by smoking. Lung Cancer Cases Proportion Smoking responsible 0. 9 Smoking not responsible 0. 1

Sampling Lung Cancer Patients Lung Cancer Cases Smoking responsible Smoking not responsible Proportion 0. 9 0. 1 How many possible outcomes are there for the two patients?

Sampling Lung Cancer Patients Lung Cancer Cases Smoking responsible Smoking not responsible Proportion 0. 9 0. 1 How many possible outcomes are there for the two patients? 2● 2 = 4

Sampling Lung Cancer Patients Lung Cancer Cases Smoking responsible Smoking not responsible Proportion 0. 9 0. 1 What are the 4 possible outcomes for the two patients?

Sampling Lung Cancer Patients Lung Cancer Cases Proportion Smoking responsible 0. 9 Smoking not responsible 0. 1 What are the possible outcomes for the two patients? 4 possible outcomes No for 1 st patient and no for 2 nd patient No for 1 st patient and yes for 2 nd patient Yes for 1 st patient and no for 2 nd patient Yes for 1 st patient and yes for 2 nd patient

Sampling Lung Cancer Patients Lung Cancer Cases Proportion Smoking responsible 0. 9 Smoking not responsible 0. 1 P(No for 1 st patient and no for 2 nd patient) = P(no for 1 st) P( no for 2 nd) = (0. 1) = 0. 01 No for 1 st patient and yes for 2 nd patient Yes for 1 st patient and no for 2 nd patient Yes for 1 st patient and yes for 2 nd patient

Sampling Lung Cancer Patients Lung Cancer Cases Proportion Smoking responsible 0. 9 Smoking not responsible 0. 1 P(No for 1 st patient and no for 2 nd patient) = P(no for 1 st) P( no for 2 nd) = (0. 1) = 0. 01 P(No, yes) = (0. 1)(0. 9) = 0. 09 P(Yes, no) = (0. 9)(0. 1) = 0. 09 P(Yes, yes) = (0. 9) = 0. 81

Sampling Lung Cancer Patients Probability distribution of X, the number of patients with lung cancer, is: x Probability of x 0 1 2

Sampling Lung Cancer Patients Probability distribution of X, the number of patients with lung cancer, is: x Probability of x 0 0. 01 1 0. 09 + 0. 09 = 0. 18 2 0. 81

Sampling Lung Cancer Patients Probability distribution of X, the number of patients with lung cancer, is: x Probability of x 0 0. 01 1 0. 18 2 0. 81

Questions?
- Slides: 72