Chapter 6 Polygons and Quadrilaterals Standard G4 The

Chapter 6 Polygons and Quadrilaterals Standard G-4: The student will demonstrate an understanding of quadrilaterals and other polygons, their properties, and relationships between or among them.

§ Objectives: § Introduction to polygons § To find the sum of the measures of interior angles of a polygon § To find the sum of the measures of exterior angles of a polygon

Key terms � Polygon � Convex polygon � Concave polygon � Equilateral polygon � Equiangular polygon � Regular polygon � Interior angles � Exterior angles

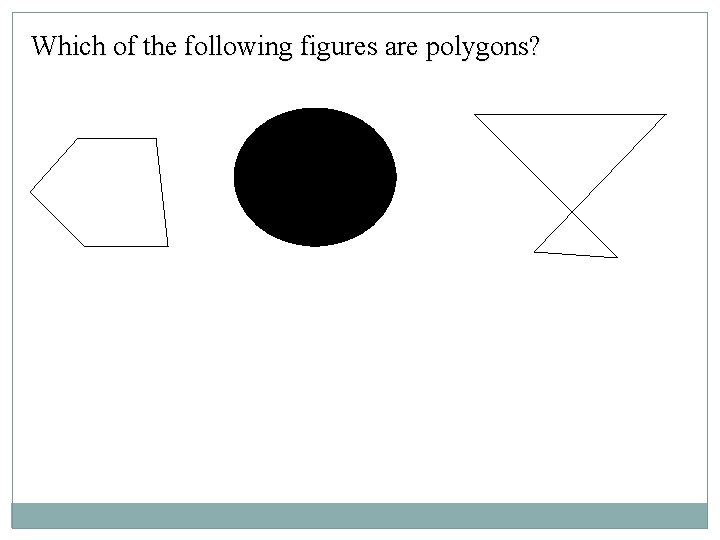
A polygon is a closed plane figure with 3 or more sides (all straight lines, no curves).

Which of the following figures are polygons?

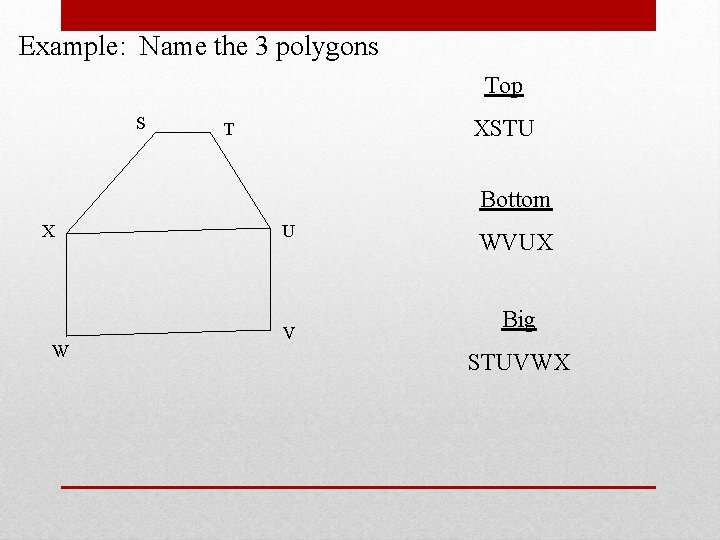
Example: Name the 3 polygons Top S XSTU T Bottom X W U V WVUX Big STUVWX

Two Types of Polygons Convex – all vertices point outward Concave – at least one vertex points inward towards the center of the polygon (The side looks like it “caved” in)

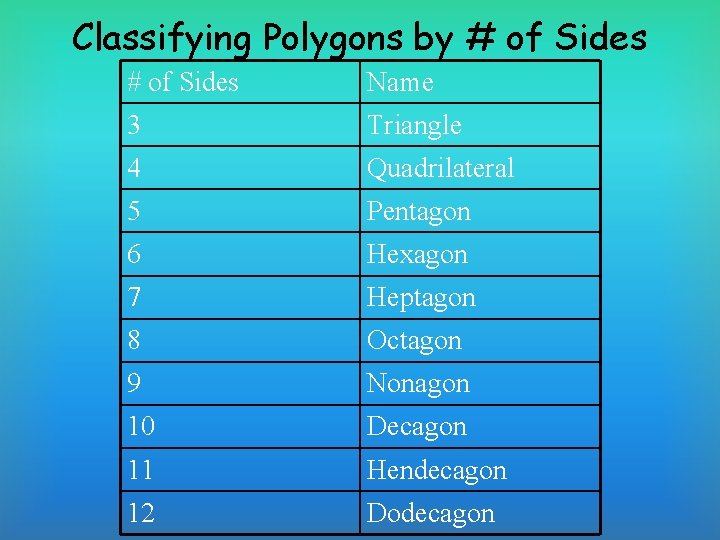
Classifying Polygons by # of Sides 3 sided Polygon = Triangle Hint: Think “Tri”cycle, “tri”pod, “Tri”lateration (Tri means 3)

Classifying Polygons by # of Sides 4 sided Polygon = Quadrilateral Hint: Think “Quad”rant, “Quad”ruple, “Quad” (AKA 4 Wheeler)

Classifying Polygons by # of Sides 5 sided Polygon = Pentagon Hint: Think “Pent”athalon, or the government building “The Pentagon”

Classifying Polygons by # of Sides 6 sided Polygon = Hexagon Hint: Both “Hexagon” and “Six” have an ‘x’ in them

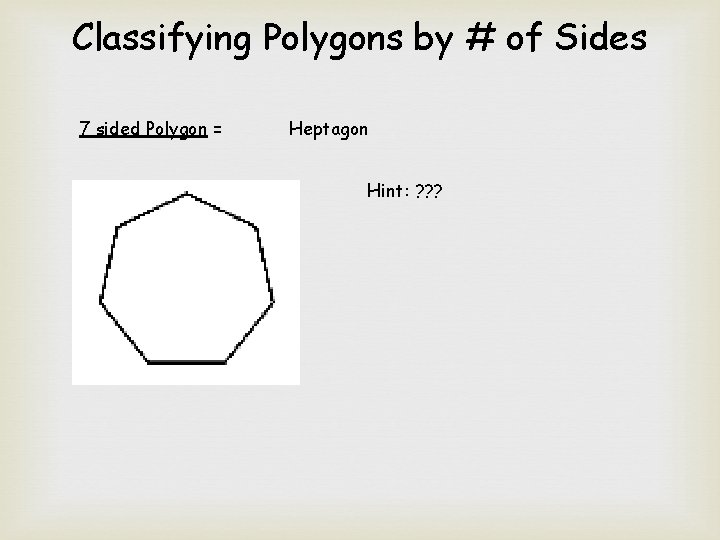
Classifying Polygons by # of Sides 7 sided Polygon = Heptagon Hint: ? ? ?

Classifying Polygons by # of Sides 8 sided Polygon = Octagon Hint: “oct”opus – 8 legs

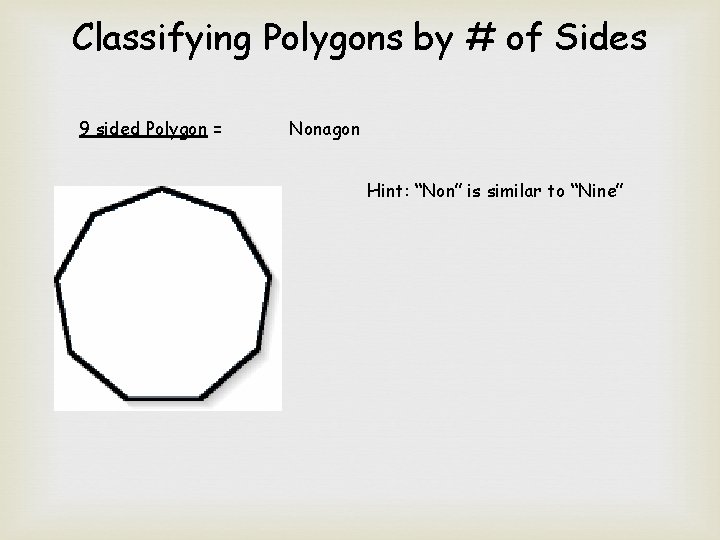
Classifying Polygons by # of Sides 9 sided Polygon = Nonagon Hint: “Non” is similar to “Nine”

Classifying Polygons by # of Sides 10 sided Polygon = Decagon Hint: Think “Dec”ade (10 years)

Classifying Polygons by # of Sides 11 sided Polygon = Hendecagon Hint: ? ? ?

Classifying Polygons by # of Sides 12 sided Polygon = Dodecagon Hint: ? ? ?

Classifying Polygons by # of Sides Q: What do we call a polygon with more than 12 sides? A: An ‘n’-gon where ‘n’ is the number of sides Ex: a 20 sided polygon is a 20 -gon

Classifying Polygons by # of Sides Name 3 Triangle 4 Quadrilateral 5 Pentagon 6 Hexagon 7 Heptagon 8 Octagon 9 Nonagon 10 Decagon 11 Hendecagon 12 Dodecagon

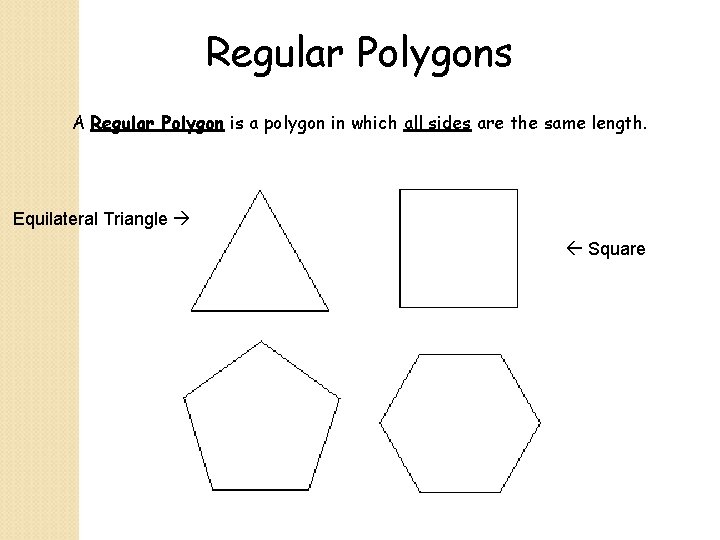
Regular Polygons A Regular Polygon is a polygon in which all sides are the same length. Equilateral Triangle Square

Polygon Angle-Sum Theorem 1

Example: Solve for x in the following example. x 100

Example: Find the measure of one interior of a regular hexagon.

Polygon Angle-Sum Theorem 2

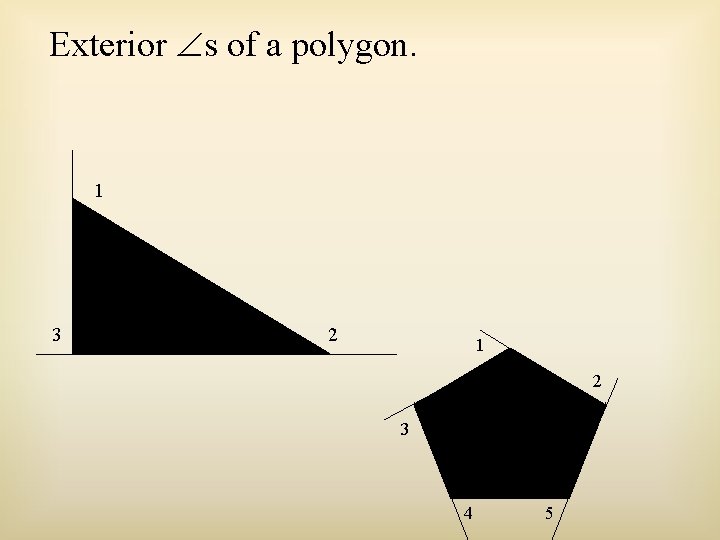
Exterior s of a polygon. 1 3 2 1 2 3 4 5

Example: How many sides does a regular polygon have if it has an exterior measure of 36°.

Example: Find the sum of the interior s of a regular polygon if it has one exterior measure of 24.

Real world connections A company is manufacturing a gear that has the shape of a regular polygon. The measure of each angle of the gear is 162. How many sides does the gear have?

Real world connections The car at each vertex of a Ferris wheel holds a maximum of 5 people. The sum of the measures of the angles of the Ferris wheel is 7740. What is the maximum number of people that the Ferris wheel can hold?

Practice/Homework Textbook: page #356 Problems: 1 -25 all problems and 29 -35 Show your work.