Chapter 6 Part A Surface analysis geometrical methods

Chapter 6 Part A: Surface analysis – geometrical methods www. spatialanalysisonline. com

Surface analysis – geometrical methods l Modelling surfaces - surfaces and fields ¡ Surfaces – typically scalar fields: l l l ¡ Surfaces - vector fields: l 3 rd edition Continuous - z-values (magnitude) assumed to exist for every (x, y) coordinate pair Real valued (may be integer coded, e. g. remote sensing data) and generally positive (may be negative) Single valued (open or 2 D manifold) – multiple values treated as separate surfaces or layers Magnitude and direction assumed to exist for every (x, y) coordinate pair www. spatialanalysisonline. com 2

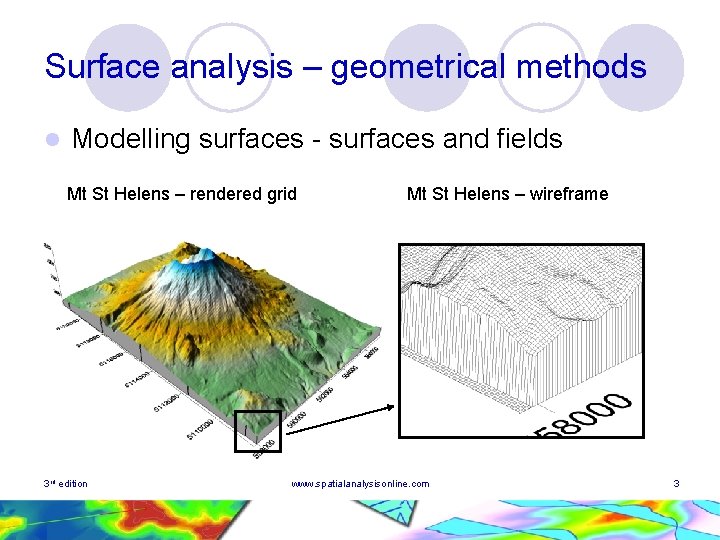
Surface analysis – geometrical methods l Modelling surfaces - surfaces and fields Mt St Helens – rendered grid 3 rd edition Mt St Helens – wireframe www. spatialanalysisonline. com 3

Surface analysis – geometrical methods l Modelling ¡ Surfaces surfaces - surfaces and fields - Data sources: • Physical surfaces – national mapping agencies, field surveys. DEM, contour, TIN or raster (image) models plus associated attribute data • Sample surveys – point/block samples converted to grids using interpolation procedures • Remote sensing – satellite, aerial • Vector data – e. g. wind strength/direction, magnetic survey data • Programmatically derived surfaces (theoretical models and best fits) 3 rd edition www. spatialanalysisonline. com 4

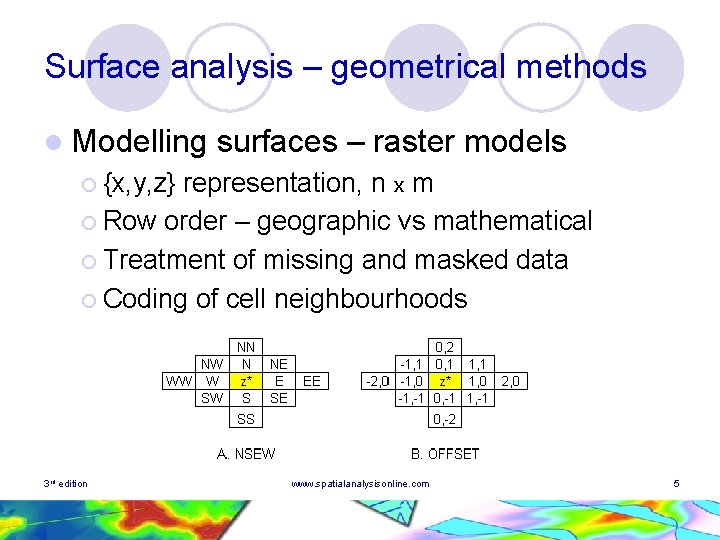
Surface analysis – geometrical methods l Modelling surfaces – raster models ¡ {x, y, z} representation, n x m ¡ Row order – geographic vs mathematical ¡ Treatment of missing and masked data ¡ Coding of cell neighbourhoods 3 rd edition www. spatialanalysisonline. com 5

Surface analysis – geometrical methods l Modelling surfaces – raster models ¡ Advantages: l l ¡ Disadvantages l l 3 rd edition Computationally very convenient Easy to display visually (2 D image and 3 D models) Aligns with some data capture (remote sensing) techniques Readily available for physical surfaces (DEM) Very large storage requirement Computation can be processor intensive Fixed grid size, shape, orientation Representation of certain objects (e. g. lines) may be poor www. spatialanalysisonline. com 6

Surface analysis – geometrical methods l Modelling ¡ Cell 3 rd edition surfaces – raster models neighbourhoods and derivatives l First order partial derivatives – finite difference model l Second order partial derivatives (simple version) www. spatialanalysisonline. com 7

Surface analysis – geometrical methods l Modelling ¡ Cell l 3 rd edition surfaces – raster models neighbourhoods and derivatives Second order partial derivatives (8 -cell finite difference version) www. spatialanalysisonline. com 8

Surface analysis – geometrical methods l Modelling surfaces – raster models ¡ Cell neighbourhoods and derivatives l Local surface models • Fit quadratic polynomial to local neighbourhood (OLS) z=ax 2+by 2+cxy+dx+ey+f (6 parameters) • Analytically differentiate • Aspect: A=tan‑ 1(e/d) • Slope: St=tan‑ 1(e 2+d 2) • Curvatures: see later slides OR • Fit partial quartic polynomial to local neighbourhood (exactly) z=ax 2 y 2+bx 2 y+cxy 2+dx 2+ey 2+fxy+gx+hy+i (9 parameters) • Curvatures: see later slides 3 rd edition www. spatialanalysisonline. com 9

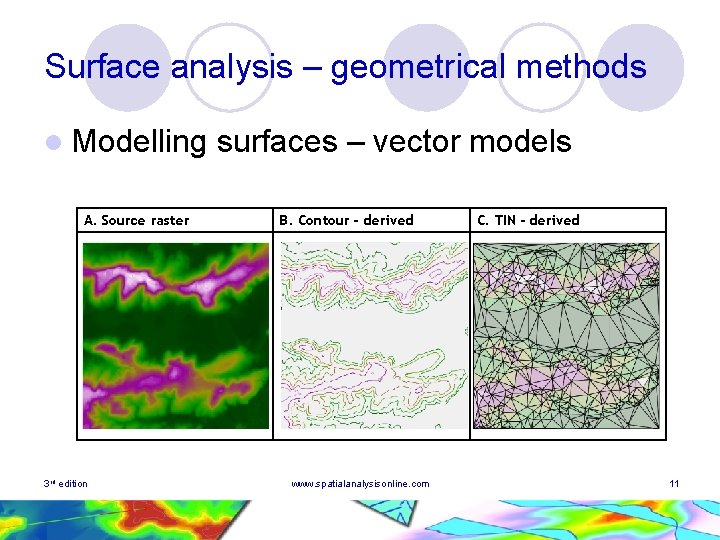
Surface analysis – geometrical methods l Modelling ¡ Principal l surfaces – vector models: TIN • Compact, fast to process • Representational detail, complexity of processing Contour – raster DEM datasets often derived from contour source material l Conversion to-from TIN/DEM l 3 rd edition www. spatialanalysisonline. com 10

Surface analysis – geometrical methods l Modelling A. Source raster 3 rd edition surfaces – vector models B. Contour - derived www. spatialanalysisonline. com C. TIN - derived 11

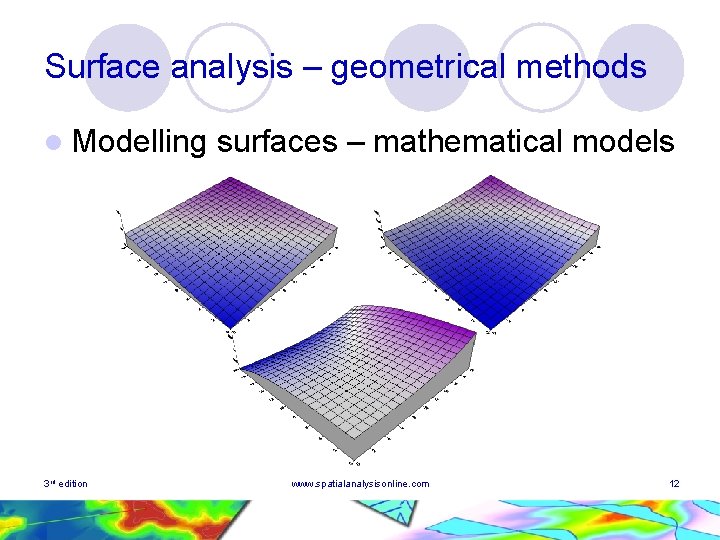
Surface analysis – geometrical methods l Modelling 3 rd edition surfaces – mathematical models www. spatialanalysisonline. com 12

Surface analysis – geometrical methods l Modelling surfaces – statistical and fractal models A. Random uniform 3 rd edition B. Random Normal www. spatialanalysisonline. com C. Ridged multi-fractal 13

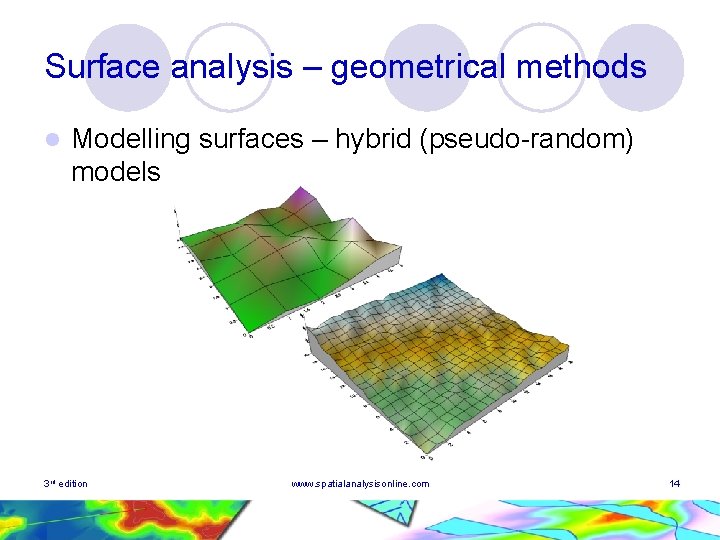
Surface analysis – geometrical methods l Modelling surfaces – hybrid (pseudo-random) models 3 rd edition www. spatialanalysisonline. com 14

Surface analysis – geometrical methods l Surface geometry – gradient, slope, aspect ¡ Gradient: vector measure – 2 components: Slope – often computed as rise over run (tan) – varies by direction. Usually defined as maximum value at a given point (magnitude component) l Aspect – direction of maximum slope (direction component) l 3 rd edition www. spatialanalysisonline. com 15

Surface analysis – geometrical methods l Surface geometry – slope models ¡ Rise over run (tan) Rise over surface distance (sin) Surface z=F(x, y) analytical differential ¡ Surface – grid differential ¡ Surface – averaging algorithms (D-infinity, 8 -point etc. ) TIN model – direct computation or conversion to grid Slope – resolution, orientation effects ¡ ¡ 3 rd edition www. spatialanalysisonline. com 16

Surface analysis – geometrical methods l Surface geometry – aspect ¡ Direction in degrees from North ¡ Directional bias from grid orientation ¡ Classified aspect – gradation, 8 -way, 4 -way ¡ Aspect and lighting/thermal modelling 3 rd edition www. spatialanalysisonline. com 17

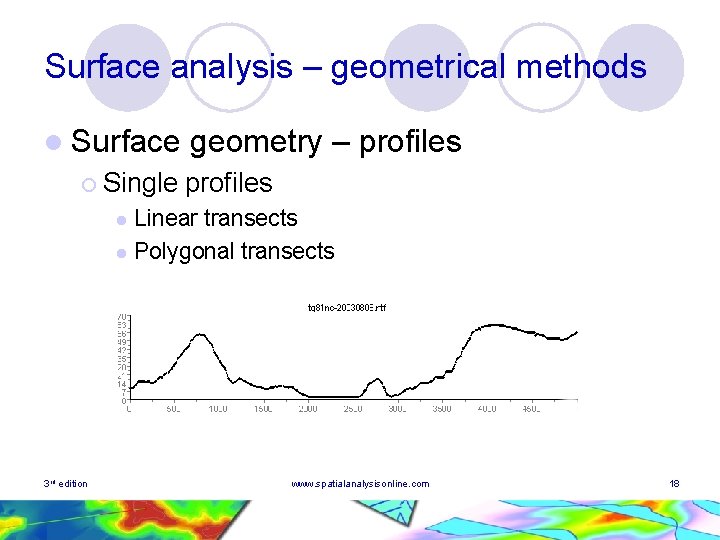
Surface analysis – geometrical methods l Surface ¡ Single geometry – profiles Linear transects l Polygonal transects l 3 rd edition www. spatialanalysisonline. com 18

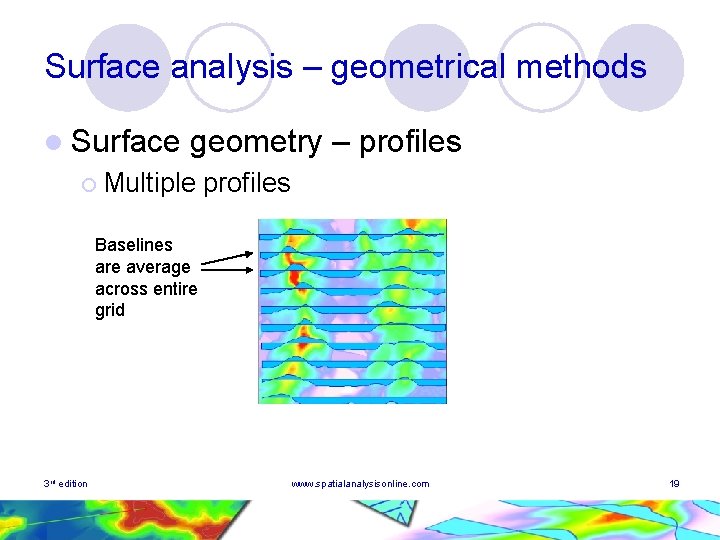
Surface analysis – geometrical methods l Surface geometry – profiles ¡ Multiple profiles Baselines are average across entire grid 3 rd edition www. spatialanalysisonline. com 19

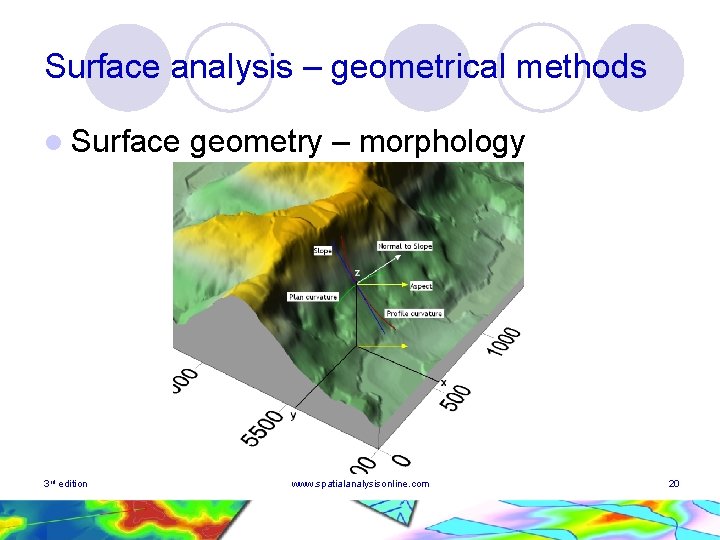
Surface analysis – geometrical methods l Surface 3 rd edition geometry – morphology www. spatialanalysisonline. com 20

Surface analysis – geometrical methods Surface geometry – curvature l ¡ Coordinate systems 1. 2. 3. ¡ 3 rd edition Original grid coordinates (x, y, z) Rotated grid coordinates (x-rot, y-rot, z) in direction of aspect Tangential coordinates (surface normal, surface tangential plane) Curvature computation and naming wrt alternative coordinate systems www. spatialanalysisonline. com 21

Surface analysis – geometrical methods l Surface ¡ Math geometry – profile curvature model: ¡ Quadratic ¡ Quartic 3 rd edition model: www. spatialanalysisonline. com 22

Surface analysis – geometrical methods l Surface ¡ Math geometry – plan curvature model: ¡ Quadratic ¡ Quartic 3 rd edition model: www. spatialanalysisonline. com 23

Surface analysis – geometrical methods l Surface 3 rd edition geometry – tangential curvature www. spatialanalysisonline. com 24

Surface analysis – geometrical methods l Surface geometry – additional quadratic curvatures ¡ Longitudinal: ¡ Cross-sectional: ¡ Min, 3 rd edition Max and mean: www. spatialanalysisonline. com 25

Surface analysis – geometrical methods l Surface geometry – directional derivatives ¡ Computed 3 rd edition for direction : l First derivative: l Second derivative: www. spatialanalysisonline. com 26

Surface analysis – geometrical methods l Surface geometry – paths ¡ Paths as plane curves ¡ Paths as space curves ¡ Parametric specification ¡ Path curvature: of curvature: 1/path curvature=1/ ¡ Smoothing ¡ Radius 3 rd edition www. spatialanalysisonline. com 27

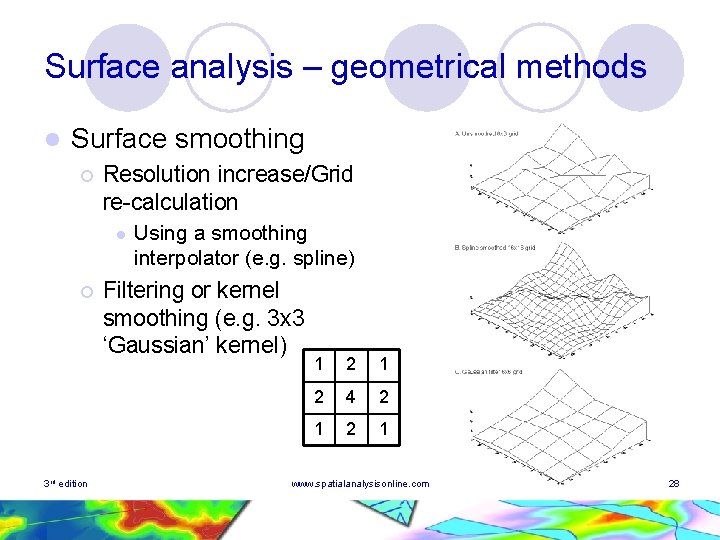
Surface analysis – geometrical methods l Surface smoothing ¡ Resolution increase/Grid re-calculation l ¡ 3 rd edition Using a smoothing interpolator (e. g. spline) Filtering or kernel smoothing (e. g. 3 x 3 ‘Gaussian’ kernel) 1 2 4 2 1 www. spatialanalysisonline. com 28

Surface analysis – geometrical methods l Surface geometry – pit filling ¡ Hydrographic modelling Prior to flow modelling l 8 -cell model and other rules l Masked fill l Depression-depth based filling l ¡ Error correction Arising from data collection l Arising from data processing (e. g. interpolation) l 3 rd edition www. spatialanalysisonline. com 29

Surface analysis – geometrical methods l Surface geometry – volumetric analysis ¡ Profiles – simple cut and fill computations ¡ Surfaces: Single grid vs reference (base) surface (e. g. z=0) l Grid pairs – grid 1 (upper), grid 2 (lower) l Result – estimate positive or negative volume (relative, and/or wrt base) l ¡ Computational procedures Numerical integration (trapezoidal rule) l Exact computation from TIN l Indirect computation from point or profile data l 3 rd edition www. spatialanalysisonline. com 30

Surface analysis – geometrical methods l Visibility – Overview ¡ Application areas ¡ Line of sight modelling ¡ Viewshed (visible areas) modelling Single and multi-point problems l Static vs dynamic problems l ¡ Optical vs radio path visibility Euclidean model l Earth curvature model l Propagation modelling l 3 rd edition www. spatialanalysisonline. com 31

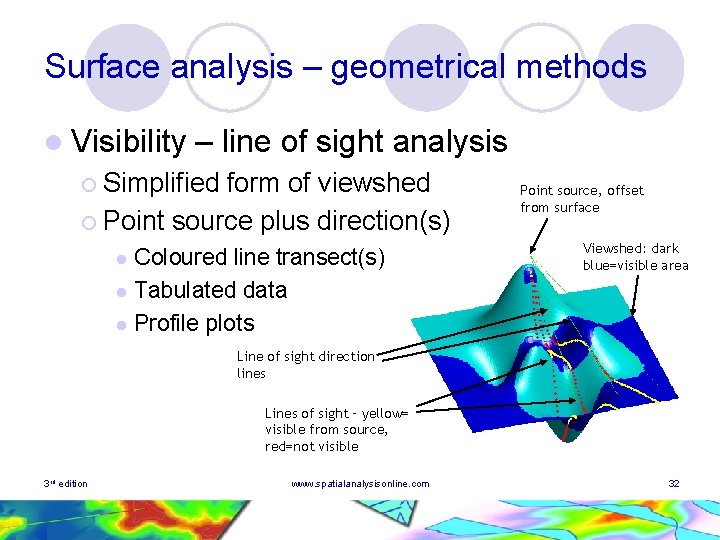
Surface analysis – geometrical methods l Visibility – line of sight analysis ¡ Simplified form of viewshed ¡ Point source plus direction(s) Coloured line transect(s) l Tabulated data l Profile plots l Point source, offset from surface Viewshed: dark blue=visible area Line of sight direction lines Lines of sight – yellow= visible from source, red=not visible 3 rd edition www. spatialanalysisonline. com 32

Surface analysis – geometrical methods l Visibility – viewsheds and RF propagation ¡ Viewshed (visible areas) modelling Input surface raster l Point set raster – single, multi-point, zones etc l Offsets for observation and target points l Range (distance and angular) constraints l Output – binary or multi-coded raster l RF – selection of propagation model, parameters (e. g. frequency, gain) and clutter modelling (typically surface offsets and obstacles) l 3 rd edition www. spatialanalysisonline. com 33

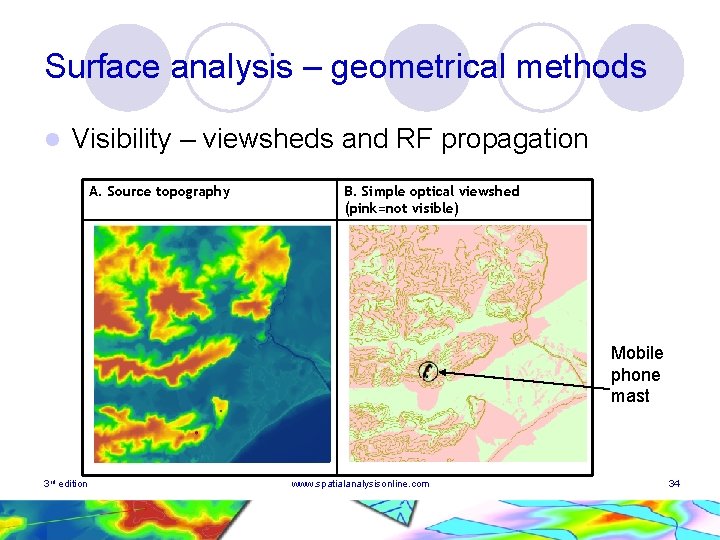
Surface analysis – geometrical methods l Visibility – viewsheds and RF propagation A. Source topography B. Simple optical viewshed (pink=not visible) Mobile phone mast 3 rd edition www. spatialanalysisonline. com 34

Surface analysis – geometrical methods l Visibility ¡ ¡ ¡ – Isovist analysis Analysis of visibility in the plane One or more source points Complex optimisation problem Near optimal locations for cameras providing full coverage of streets Sample point – green areas show visible street areas 3 rd edition www. spatialanalysisonline. com 35

Surface analysis – geometrical methods l Visibility ¡ 3 rd edition – Space syntax Analysis of visibility in the built environment www. spatialanalysisonline. com 36

Surface analysis – geometrical methods l Watersheds and drainage – assumptions ¡ Uniform precipitation ¡ Flows take place entirely across surfaces which they do not alter; unaffected by absorption or groundwater ¡ Flows grow as a linear function with distance; not altered by slope values, just by direction ¡ No barriers to flow ¡ Study region is complete and meaningful in the context of the analysis 3 rd edition www. spatialanalysisonline. com 37

Surface analysis – geometrical methods l Watersheds and drainage – modelling steps ¡ Input (complete/mosaic-ed) DEM ¡ Remove pits ¡ Identify flow directions – D-8, D-infinity or MFM ¡ Output ldd grid ¡ Identify flats and extrema ¡ Accumulate hypothetical flows to generate and merge streams – include pour points ¡ Identify watersheds and stream basins 3 rd edition www. spatialanalysisonline. com 38

Surface analysis – geometrical methods l Watersheds and drainage – D-infinity ¡ Max gradient of 8 facets identified ¡ Flows assigned to cells (pixels) in proportions: 3 rd edition www. spatialanalysisonline. com 39

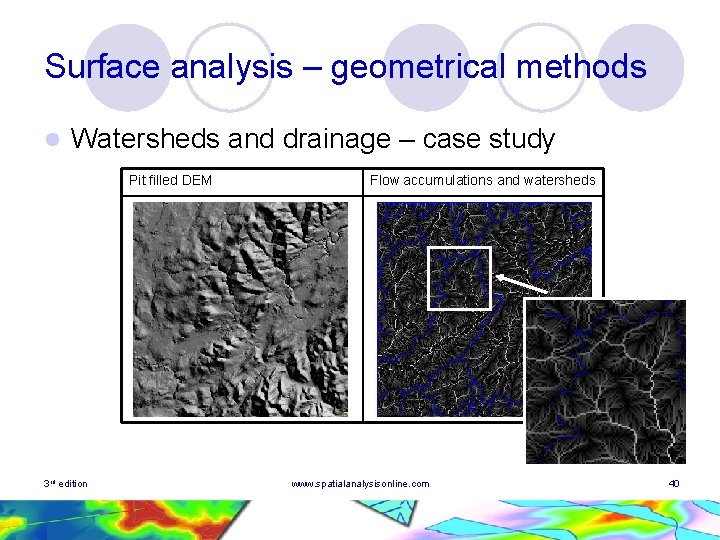
Surface analysis – geometrical methods l Watersheds and drainage – case study Pit filled DEM 3 rd edition Flow accumulations and watersheds www. spatialanalysisonline. com 40

Surface analysis – geometrical methods l Watersheds and drainage – case study Flats and extrema 3 rd edition Stream basins www. spatialanalysisonline. com 41