Chapter 6 Part 1 Array Implementation 1 0

Chapter 6 Part 1

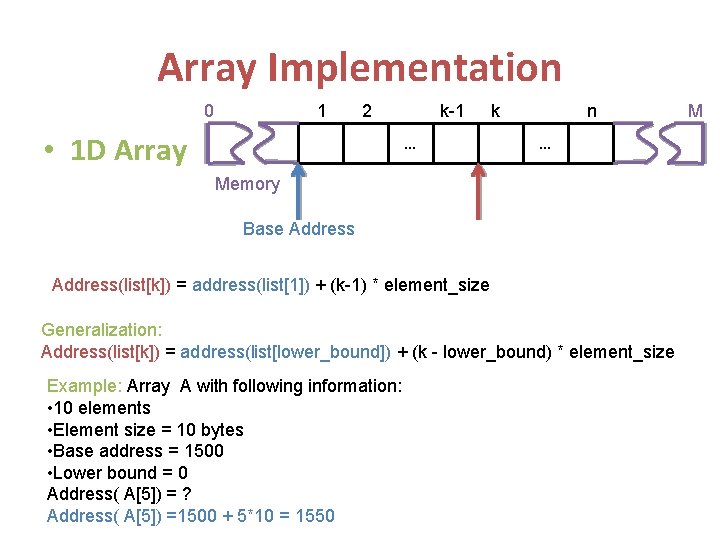
Array Implementation 1 0 2 • 1 D Array k-1 … k n … Memory Base Address(list[k]) = address(list[1]) + (k-1) * element_size Generalization: Address(list[k]) = address(list[lower_bound]) + (k - lower_bound) * element_size Example: Array A with following information: • 10 elements • Element size = 10 bytes • Base address = 1500 • Lower bound = 0 Address( A[5]) = ? Address( A[5]) =1500 + 5*10 = 1550 M

2 D Arrays 2 common ways for mapping 2 D arrays to 1 D: 1) Row Major Order 2) Column Major Order Ex: 3 4 6 2 1 3 7 5 8 Would be stored as 3, 4, 7, 6, 2, 5, 1, 3, 8 7 5 8 Would be stored as 3, 6, 1, 4, 2, 3, 7, 5, 8

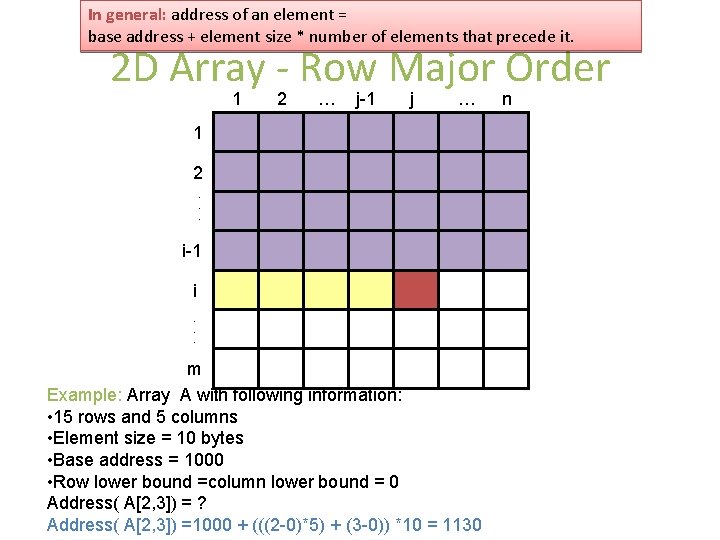
In general: address of an element = base address + element size * number of elements that precede it. 2 D Array - Row Major Order 1 1 2. . . i-1 i. . . m 2 … j-1 j … n

In general: address of an element = base address + element size * number of elements that precede it. 2 D Array - Row Major Order 1 1 2. . . i-1 i. . . m 2 … j-1 j … n

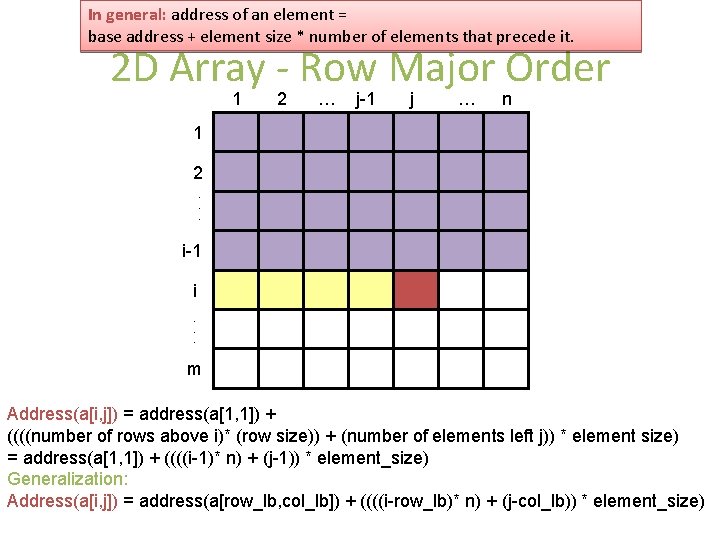
In general: address of an element = base address + element size * number of elements that precede it. 2 D Array - Row Major Order 1 2 … j-1 j … n 1 2. . . i-1 i. . . m Address(a[i, j]) = address(a[1, 1]) + ((((number of rows above i)* (row size)) + (number of elements left j)) * element size) = address(a[1, 1]) + ((((i-1)* n) + (j-1)) * element_size) Generalization: Address(a[i, j]) = address(a[row_lb, col_lb]) + ((((i-row_lb)* n) + (j-col_lb)) * element_size)

In general: address of an element = base address + element size * number of elements that precede it. 2 D Array - Row Major Order 1 2 … j-1 j … 1 2. . . i-1 i. . . m Example: Array A with following information: • 15 rows and 5 columns • Element size = 10 bytes • Base address = 1000 • Row lower bound =column lower bound = 0 Address( A[2, 3]) = ? Address( A[2, 3]) =1000 + (((2 -0)*5) + (3 -0)) *10 = 1130 n

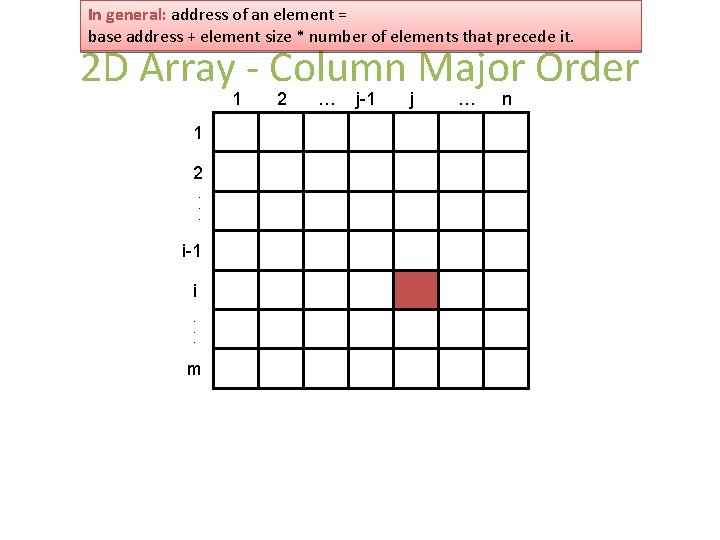
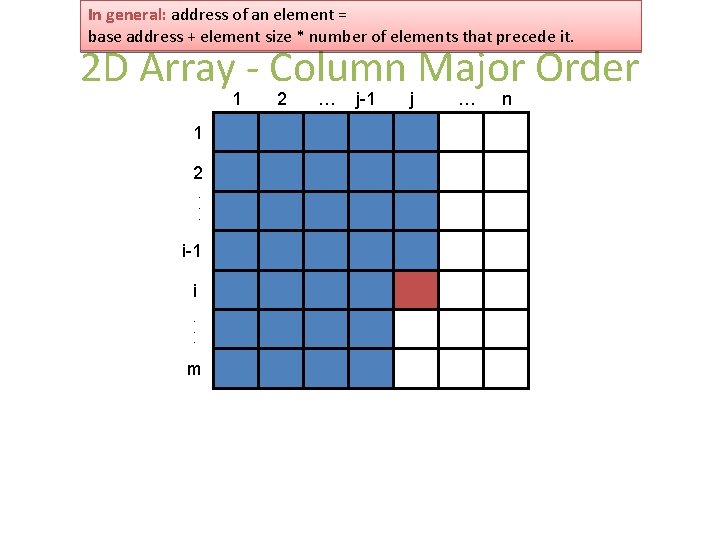
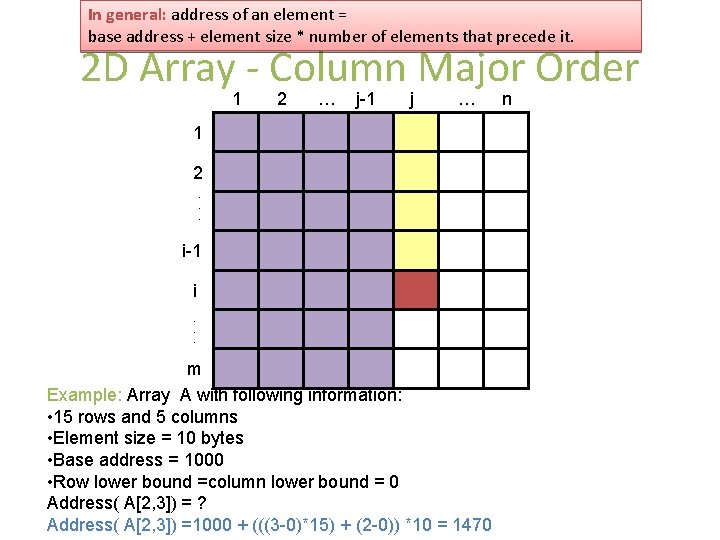
In general: address of an element = base address + element size * number of elements that precede it. 2 D Array - Column Major Order 1 1 2. . . i-1 i. . . m 2 … j-1 j … n

In general: address of an element = base address + element size * number of elements that precede it. 2 D Array - Column Major Order 1 1 2. . . i-1 i. . . m 2 … j-1 j … n

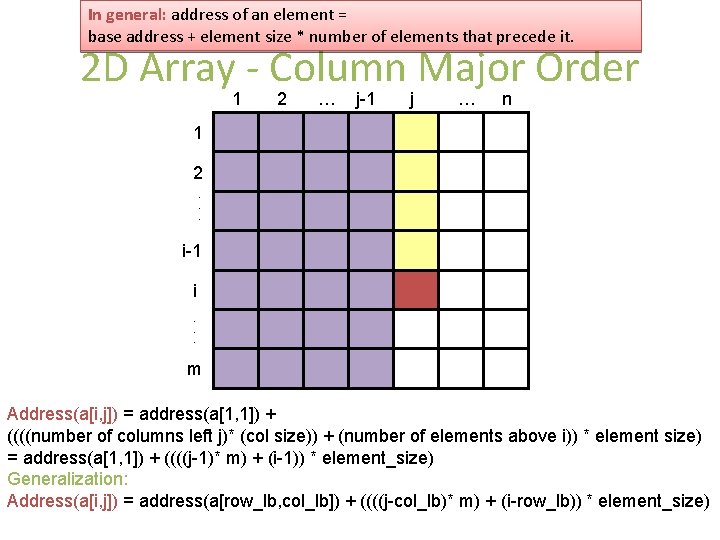
In general: address of an element = base address + element size * number of elements that precede it. 2 D Array - Column Major Order 1 2 … j-1 j … n 1 2. . . i-1 i. . . m Address(a[i, j]) = address(a[1, 1]) + ((((number of columns left j)* (col size)) + (number of elements above i)) * element size) = address(a[1, 1]) + ((((j-1)* m) + (i-1)) * element_size) Generalization: Address(a[i, j]) = address(a[row_lb, col_lb]) + ((((j-col_lb)* m) + (i-row_lb)) * element_size)

In general: address of an element = base address + element size * number of elements that precede it. 2 D Array - Column Major Order 1 2 … j-1 j … 1 2. . . i-1 i. . . m Example: Array A with following information: • 15 rows and 5 columns • Element size = 10 bytes • Base address = 1000 • Row lower bound =column lower bound = 0 Address( A[2, 3]) = ? Address( A[2, 3]) =1000 + (((3 -0)*15) + (2 -0)) *10 = 1470 n

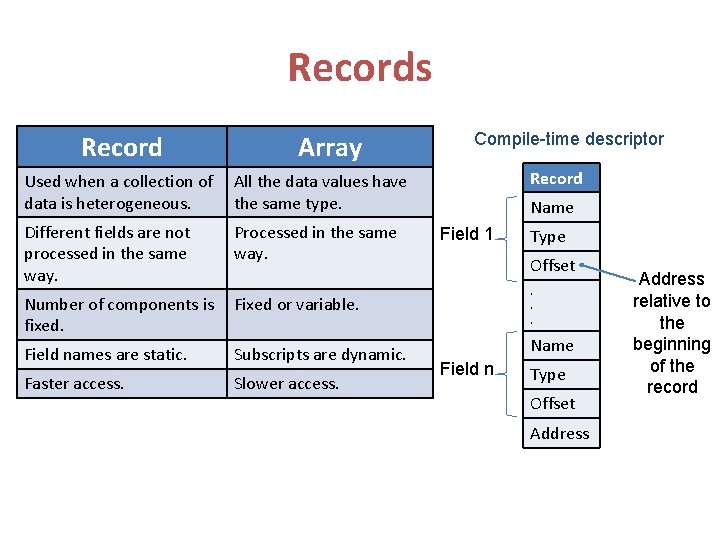
Records Record Array Used when a collection of data is heterogeneous. All the data values have the same type. Different fields are not processed in the same way. Processed in the same way. Number of components is fixed. Fixed or variable. Field names are static. Subscripts are dynamic. Faster access. Slower access. Compile-time descriptor Record Name Field 1 Type Offset. . . Name Field n Type Offset Address relative to the beginning of the record

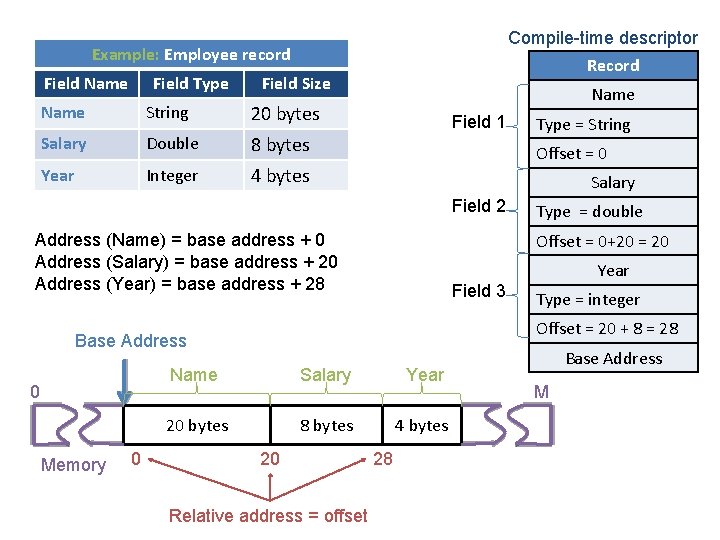
Compile-time descriptor Example: Employee record Field Name Field Type Record Field Size Name String 20 bytes Salary Double 8 bytes Year Integer 4 bytes Name Field 1 Offset = 0 Salary Field 2 Field 3 0 Year Type = integer Offset = 20 + 8 = 28 Base Address Memory Type = double Offset = 0+20 = 20 Address (Name) = base address + 0 Address (Salary) = base address + 20 Address (Year) = base address + 28 0 Type = String Name Salary Year 20 bytes 8 bytes 4 bytes 20 Relative address = offset 28 Base Address M

Union • A union is a type that may store different type values at different times during execution.

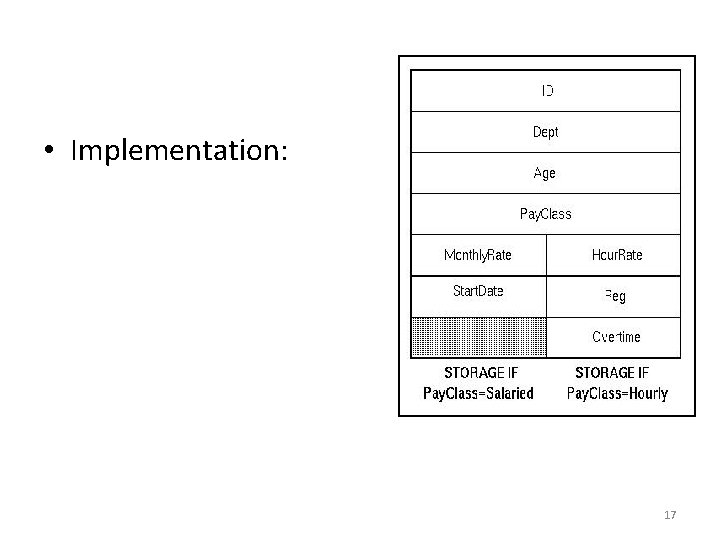
Variant Records • A single record type with several variants. • Specification: – In Pascal: Common part Variant part type Pay. Type=(Salaried, Hourly); var Employee: record ID : integer; Dept: array[1. . 3] of char; Age : integer; case Pay. Class : Pay. Type of Salaried: (Monthly. Rate: real; Start. Date : integer); Hourly : (Hour. Rate: real; Reg : integer; Overtime: integer) end 15

– In C: (use the ‘union’ keyword) Common part Variant part typedef enum {Salaried, Hourly} Pay. Type; typedef struct { int ID; char Dept[3]; int Age; Pay. Type Pay. Class; Pay. Variant pay; } Employee. Record; Employee. Record Employee; typedef struct { float Monthly. Rate; int Start. Date; } Salaried. Type ; typedef struct { float Hour. Rate; int Reg, Overtime; } Hourly. Type ; typedef union { Salaried. Type sal_type; Hourly. Type hour_type; } Pay. Variant ; 16

• Implementation: 17