Chapter 6 Numerical Methods for Ordinary Differential Equations





































































- Slides: 77

Chapter 6 Numerical Methods for Ordinary Differential Equations 1

6. 1 The Initial Value Problem: Background 2

Example 6. 1 3

Example 6. 2 4

Example 6. 3 5

Example 6. 4 6

Methods l To solve differential equation problem: – If f is “smooth enough”, then l l – Two ways of expressing “smooth enough” l l 7 a solution will exist and be unique we will be able to approximate it accurately with a wide variety of method Lipschitz continuity Smooth and uniformly monotone decreasing

Definitions 6. 1 and 6. 2 8

Example 6. 5 9

Example 6. 5 (con. ) 10

Theorem 6. 1 l 11 Proof: See Goldstine’s book

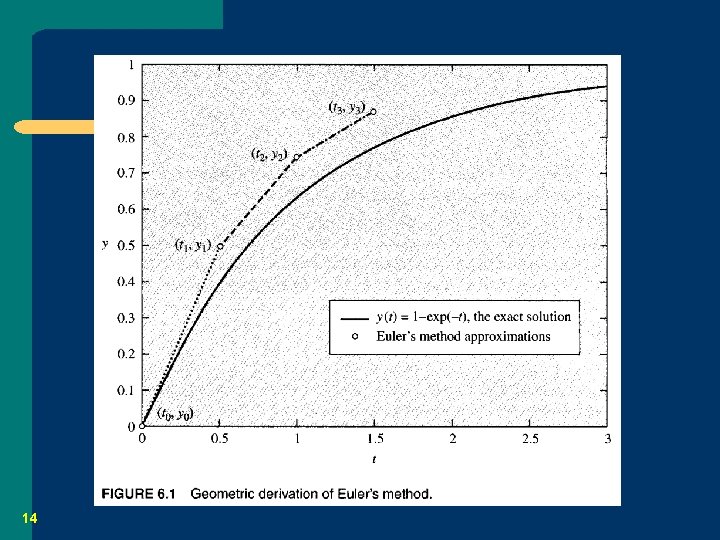
6. 2 Euler’s Method l l We have treated Euler’s method in Chapter 2. There are two main derivations about Euler’s method – – 12 Geometric derivation Analytic derivation

Geometric Derivation 13

14

Analytic Derivation 15

Error Estimation for Euler’s Method 16 l By the analytic derivation, we have l The residual for Euler’s method: l The truncation error:

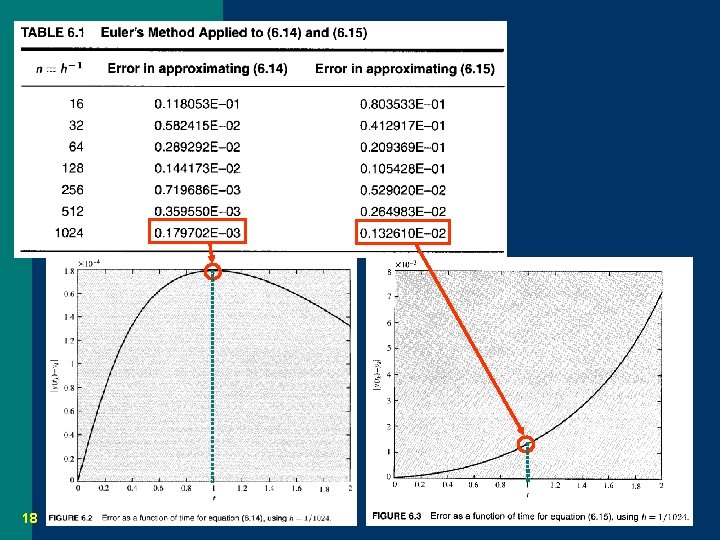
Example 6. 6 17

18

6. 3 Analysis of Euler’s Method O(h) l 19 Proof: pp. 323 -324 (You can study it by yourselves. )

Theorem 6. 4 O(h) l 20 Proof: pp. 324 -325 (You can study it by yourselves. )

Discussion l Both error theorems show that Euler’s method is only first-order accurate (O(h)). – – 21 If f is only Lipschitz continuous, then the constants multiplying the initial error and the mash parameter can be quite large, rapidly growing. If f is smooth and uniformly monotone decreasing in y, then the constants in the error estimate are bounded for all n.

Discussion l How is the initial error affected by f ? – – 22 If f is monotone decreasing in y, then the effect of the initial error decreases rapidly as the computation progresses. If f is only Lipschitz continuous, then any initial error that is made could be amplified to something exponentially large.

6. 4 Variants of Euler’s Method l l 23 Euler’s method is not the only or even the best scheme for approximating solutions to initial value problems. Several ideas can be considered based on some simple extensions of one derivation of Euler’s method.

Variants of Euler’s Method l We start with the differential equation And replace the derivative with the simple difference quotient derived in (2. 1) l 24 What happens if we use other approximations to the derivative?

Variants of Euler’s Method l If we use O(h) then we Method 1 get the backward Euler method l If we use then we 2 get the midpoint method Method 25 O(h 2)

Variants of Euler’s Method l O(h 2) If we use the methods based on interpolation (Section 4. 5) O(h 2) Method 3 then we get two numerical methods Method 4 26

Variants of Euler’s Method l By integrating the differential equation: (6. 23) and apply the trapezoid rule to (6. 23) to get O(h 3) Thus Method 5 27 (6. 25)

Variants of Euler’s Method O(h 3) l We can use a midpoint rule approximation to Method 6 integrating (6. 23) and get 28

Discussion l l What about these method? Are any of them any good? Observations – – – 29 Methods 2, 3, and 4 are all based on derivative approximations that are O(h 2), thus they are more accurate than Euler method and method 1 (O(h)). Similarly, methods 5 and 6 are also more accurate. Methods 2, 3, and 4 are not single-step methods, but multistep methods. They depend on information form more than one previous approximate value of the unknown function.

Discussion l Observations (con. ) – – 30 Concerning methods 1, 4, and 5, all of these formulas involve we cannot explicitly solve for the new approximate values Thus these methods are called implicit methods. Methods 2 and 3 are called explicit methods.

6. 4. 1 The Residual and Truncation Error 31

Definition 6. 3 32

Example 6. 7 33

Example 6. 8 34

Definition 6. 4 35

6. 4. 2 Implicit Methods and Predictor. Corrector Schemes l How to get the value of yn+1? Using Newton’s method or the secant method or a fixed point iteration. Let y = yn+1 36

F(y) F’(y) F(y) h F(y+h)-F(y) 37

Predictor-corrector idea l 38 Can we use a much cruder (coarse) means of estimating yn+1?

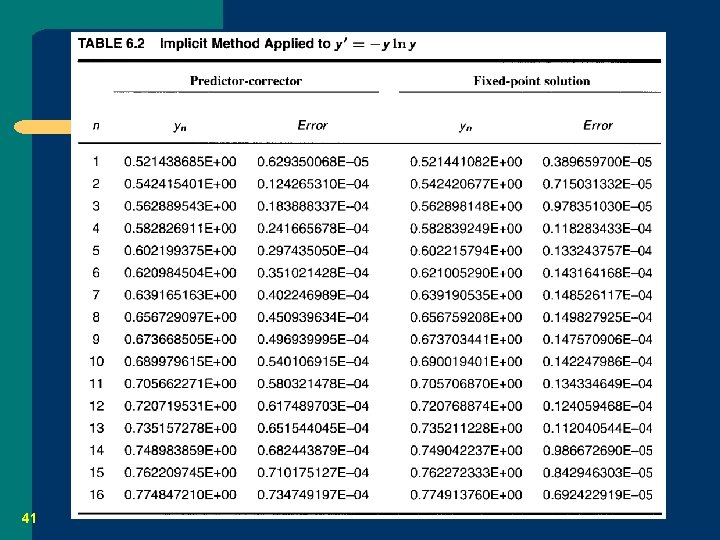
Example 6. 11 39

Example 6. 12 40

41

Discussion l 42 Generally speaking, unless the differential equation is very sensitive to changes in the data, a simple predictor-corrector method will be just as good as the more time-consuming process of solving for the exact values of yn+1 that satisfies the implicit recursion.

Discussion l l 43 If the differential equation is linear, we can entirely avoid the problem of implicitness. Write the general linear ODE as

6. 4. 3 Starting Values and Multistep Method l 44 How to find the starting values?

Example 6. 15 (con. ) 45

Example 6. 15 (con. ) 46

47

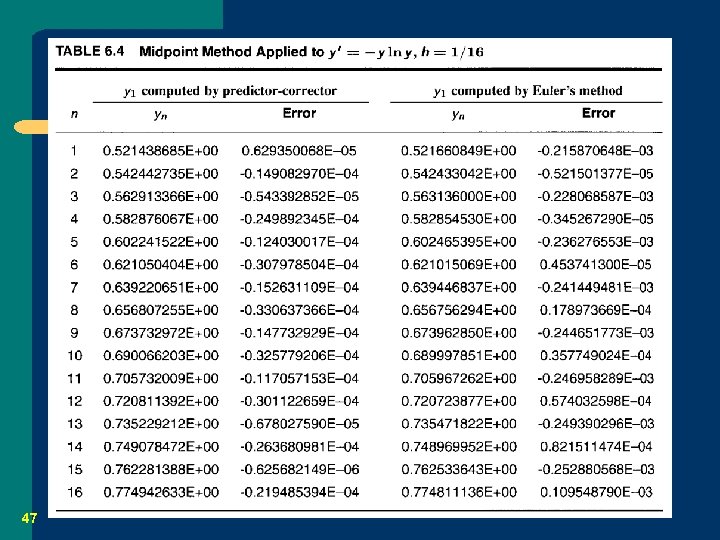
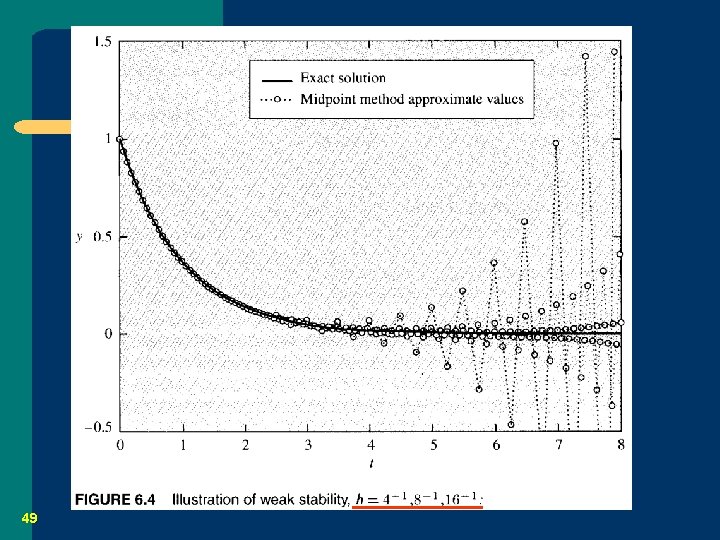
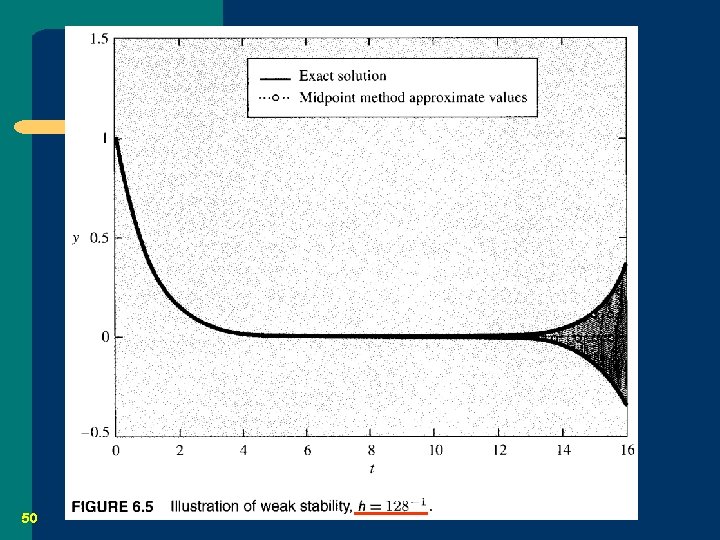
6. 4. 4 The Midpoint Method and Weak Stability 48

49

50

Discussion l What is going on here? – – 51 It is the weakly stability problem. The problem is not caused by rounding error. The problem is inherent in the midpoint method and would occur in exact arithmetic. Why? (pp. 340 -342)

6. 5 Single-step Method: Runge-Kutta l 52 The Runge-Kutta family of methods is one of the most popular families of accurate solvers for initial value problems.

l Consider the more general method: Residual 53

54

l 55 Rewrite the formula of R, we get

Solution 1 Solution 2 56

Solution 3 57

Runge-Kutta Method 58

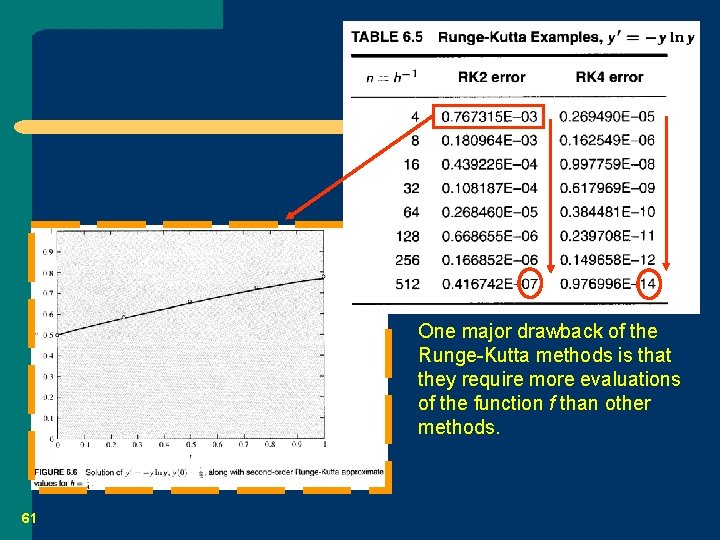
Example 6. 16 59

Example 6. 16 (con. ) 60

One major drawback of the Runge-Kutta methods is that they require more evaluations of the function f than other methods. 61

6. 6 Multistep Methods 6. 6. 1 The Adams families l Adams families include the following most popular ones: – – 62 Explicit methods: Adams-Bashforth families Implicit methods: Adams-Moulton families

Adams-Bashforth Methods 63

64

Discussion l 65 If we assume a uniform grid with mash spacing h, then the formulas for the and simplify substantially, and they are routinely tabulated:

Example 6. 17 Table 6. 6 66

Example 6. 17 (con. ) Table 6. 6 67

Adams-Moulton Methods If k = -1 then tn-k= tn+1 68

Example 6. 18 69

70

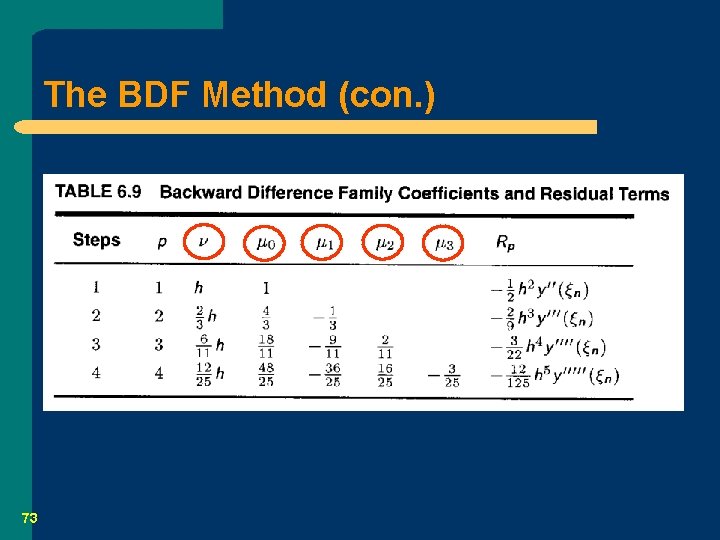
6. 6. 2 The BDF Family l 71 BDF: backward difference formula

The BDF Method (con. ) K = -1 72

The BDF Method (con. ) 73

6. 7 Stability Issues 74

Definition 6. 6 75

Discussion 76

Example 6. 19 77