Chapter 6 Multiple Integrals Chapter Outline Double and

Chapter 6 Multiple Integrals

Chapter Outline Double and Triple Integrals in Cartesian Coordinates q Double Integrals in Polar Coordinates q Triple Integrals in Cylindrical and Spherical Coordinates. q

Double Integral in Cartesian Coordinates Definition: The double integral of f over the rectangle R is if limit exists. The sample point the sub-rectangles. If f is continuous then can be chosen to be any point in

Example: Evaluate the integrals a) Solution: a) b) b)

Fubini’s Theorem:

Properties of Double Integrals:

Triple Integral in Cartesian Coordinates Definiton: The triple integral of f over box D is if limit exists. If f is continuous then, the above can become simple as Fubini’s Theorem for Triple Integrals: If f is continuous on the rectangular box D=[a, b]x[c, d]x[r, s] then

Example: Evaluate the triple integral xyz 2 dv, where D is the Rectangular box given by D={(x, y, z) l 0≤x≤ 1, -1≤y≤ 2, 0≤z≤ 3}. Solution:

Double Integrals in Polar Coorinates: If f is continuous on a Polar rectangle R given by 0≤a≤r≤b , α≤θ≤β where 0≤ β-α≤ 2π, then Example: Evaluate (3 x+4 y 2)d. A, where R is the region in the upper half-plane bounded by the circle x 2+y 2=1 & x 2+y 2=4. Solution: The region R can be described as R={(x, y) l y≥ 0, 1≤x 2+y 2≤ 4} It is the half-ring & in polar-coordinates it is given by 1≤r≤ 2, 0≤ θ≤π.

Triple Integrals in Cylindrical Coordinates: Formula for triple integration in cylindrical coordinates is Example: Evaluate Solution: E={(x, y, z)l-2≤x ≤ 2, ≤y≤ , ≤ z ≤ 2} The projection of E on the xy-plane is the disk x 2+y 2≤ 4. The lower surface of E is the cone z= & its upper surface is the plane z=2.

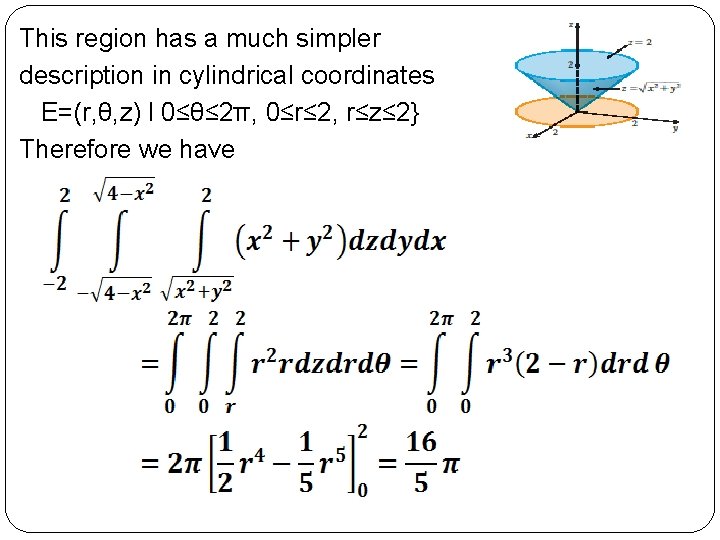
This region has a much simpler description in cylindrical coordinates E=(r, θ, z) l 0≤θ≤ 2π, 0≤r≤ 2, r≤z≤ 2} Therefore we have

Triple Integrals in Spherical Coordinates: Formula for triple integration in spherical coordinates is Where D is a Spherical wedge given by D={(ρ, θ, ϕ) | a≤ρ≤b, α≤θ≤β, c≤ϕ≤d} Example: Evaluate , where D is the unit ball: D={(x, y, z) | x 2+y 2+z 2 ≤ 1} Solution: Since the boundary of D is a sphere, we use spherical coordinates D={(ρ, θ, ϕ) | 0≤ρ≤ 1, 0≤θ≤ 2π, 0≤ϕ≤π}

In addition, spherical coordinates are appropriate because x 2+y 2+z 2 = ρ2.