Chapter 6 Motion in Two Dimensions I Projectile

I. Projectile Motion • Objects shot through the air are called projectiles • Objects

• The only force acting on a projectile, when air resistance is ignored,

• A projectile’s vertical motion increases in downward velocity because of the acceleration

• A projectile’s horizontal motion has constant velocity because there is no horizontal

• A combination of constant horizontal velocity and uniform vertical acceleration produces a

A. Projectiles Launched at an Angle • When a projectile is launched at an

• The projectile will rise with slowing speed, reach the top of its

• Other quantities can be measured such as a projectile’s maximum height, range,

II. Circular Motion • Remember acceleration is a vector and has both magnitude and

• To find the object’s velocity, you need to find its displacement vector,

• The velocity of the object is at right angles to the position

• The acceleration of the object does not change in magnitude and always

A. Centripetal Acceleration • A triangle made from the position vectors and a triangle

• The equation is not changed if both sides are divided by Δt

• Velocity can be measured by calculating how long it takes an object

• Substituting this variable in the acceleration equation (2πr/T)2 4π2 r ac =

B. Centripetal Force • There is always a net force toward the center of

C. Centrifugal Force • According to Newton’s First Law, an object in motion will

III. Relative Velocity • When velocities are along the same line, simple addition or

Slides: 21

Download presentation

Chapter 6 Motion in Two Dimensions

I. Projectile Motion • Objects shot through the air are called projectiles • Objects often follow a curved path like a parabola • An objects path through space is called its trajectory

• The only force acting on a projectile, when air resistance is ignored, is the field force of gravity in the downward direction

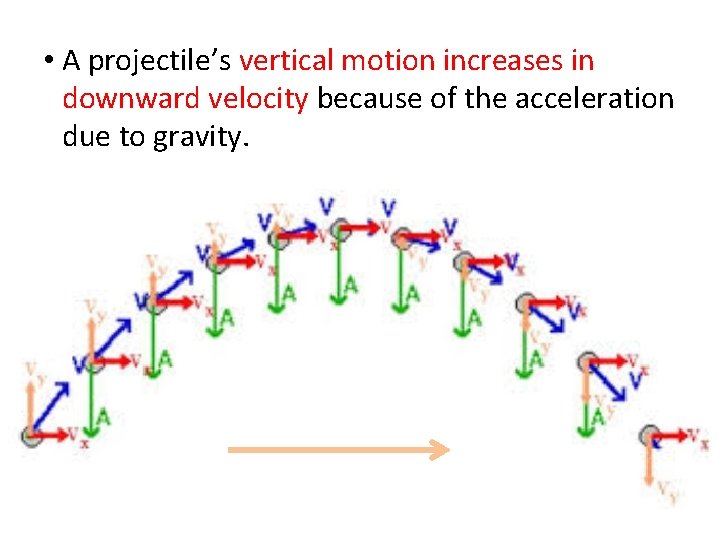
• A projectile’s vertical motion increases in downward velocity because of the acceleration due to gravity.

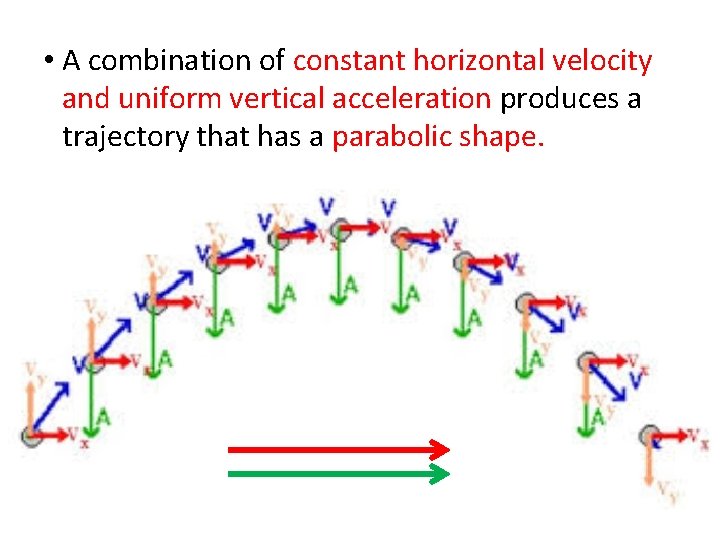
• A projectile’s horizontal motion has constant velocity because there is no horizontal force acting on the ball.

• A combination of constant horizontal velocity and uniform vertical acceleration produces a trajectory that has a parabolic shape.

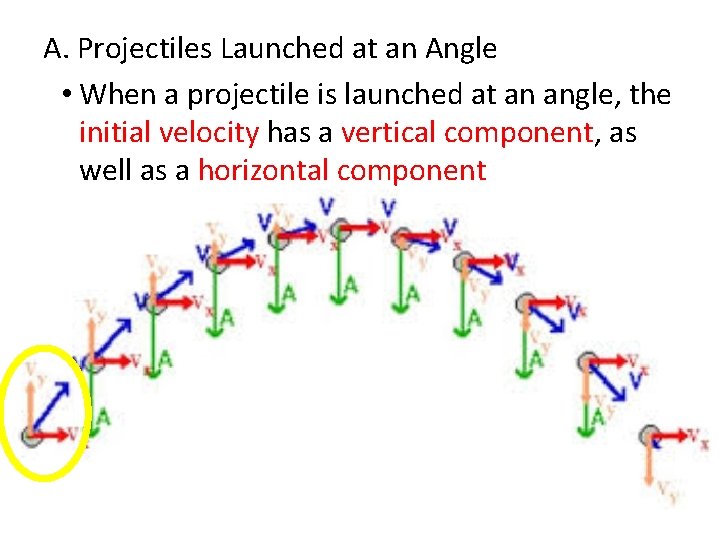
A. Projectiles Launched at an Angle • When a projectile is launched at an angle, the initial velocity has a vertical component, as well as a horizontal component

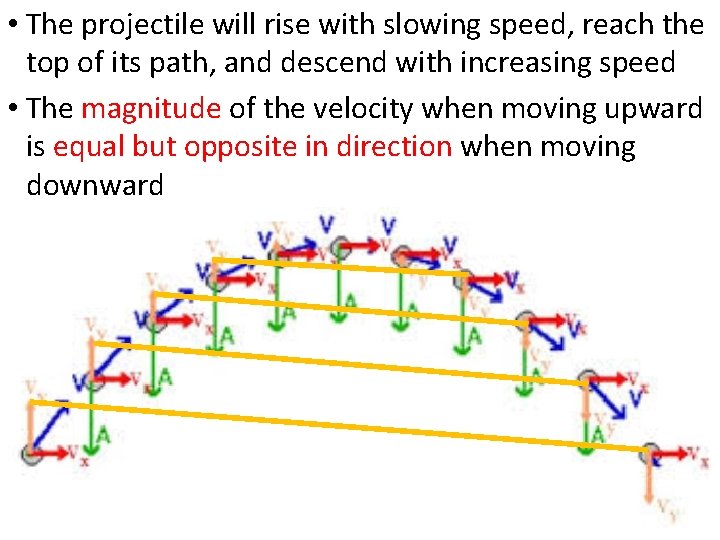
• The projectile will rise with slowing speed, reach the top of its path, and descend with increasing speed • The magnitude of the velocity when moving upward is equal but opposite in direction when moving downward

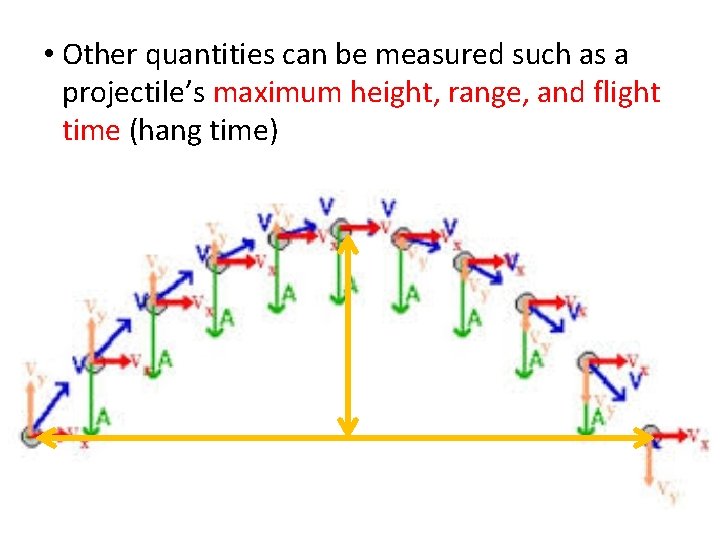
• Other quantities can be measured such as a projectile’s maximum height, range, and flight time (hang time)

II. Circular Motion • Remember acceleration is a vector and has both magnitude and direction • Objects moving in a circle at constant speed are accelerating because they are changing direction, r

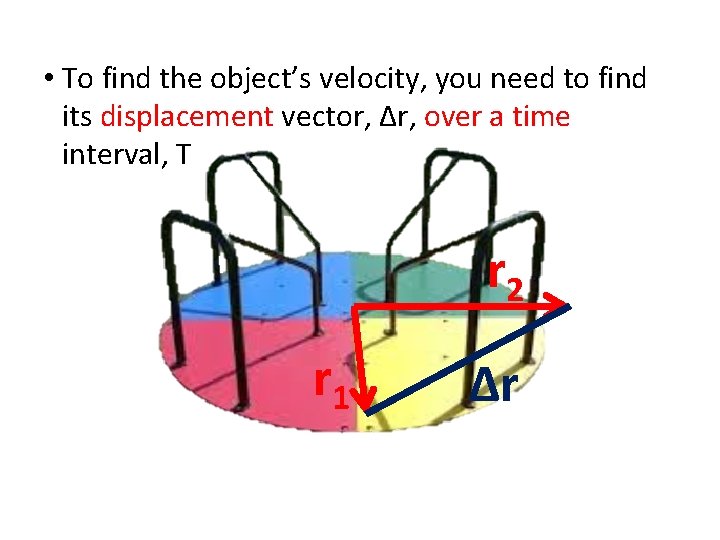
• To find the object’s velocity, you need to find its displacement vector, Δr, over a time interval, T r 2 r 1 Δr

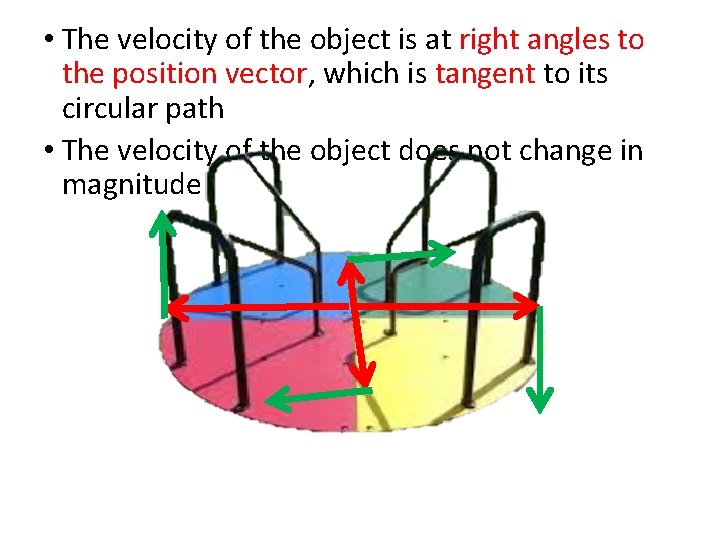
• The velocity of the object is at right angles to the position vector, which is tangent to its circular path • The velocity of the object does not change in magnitude

• The acceleration of the object does not change in magnitude and always points in toward the center of the circle - the acceleration is called center-seeking, or centripetal acceleration

A. Centripetal Acceleration • A triangle made from the position vectors and a triangle made from the velocity vectors are similar triangles • The ratios of the lengths of corresponding sides are equal Δr = Δv r v

• The equation is not changed if both sides are divided by Δt _Δr_ = _Δv_ rΔt vΔt

• Remember: v = Δr / Δt a = Δv / Δt • So: v=a r v • Solving for centripetal acceleration, or ac v 2 ac = r

• Velocity can be measured by calculating how long it takes an object to make one complete revolution in a given time interval, T Circumference of a circle = 2πr v= T

• Substituting this variable in the acceleration equation (2πr/T)2 4π2 r ac = r = T 2

B. Centripetal Force • There is always a net force toward the center of the circle, or centripetal force • Newton’s second law says F = m⋅a Fnet = m⋅ac • When the force of an object is released, it flies off in the direction of its velocity, which is tangent to the circle

C. Centrifugal Force • According to Newton’s First Law, an object in motion will stay in motion unless a net force is acting on the object • A centrifugal force, or outward force, is a fictitious, nonexistent force - Noticed when a passenger, in a car turning left, moves right

III. Relative Velocity • When velocities are along the same line, simple addition or subtraction can be used to determine the relative velocity va/b + vb/c = va/c