Chapter 6 List and Iterators 2004 Goodrich Tamassia

Chapter 6 List and Iterators © 2004 Goodrich, Tamassia Lists and Iterators 1

6. 1 Array Lists (Vectors) © 2004 Goodrich, Tamassia Lists and Iterators 2

Definitions: List (Sequence): - It’s a collection S of n elements stored in a certain linear order, so that we can refer to the elements in S as first, second, third, and so on. - Each element e in S can be uniquely referred to by an integer in the range 0 to n-1. Index of Element: - The index of an element e in S is the number of elements that precede e in S. - First element in S has index 0, last element has index n-1. - Also, if an element in S has index i, its previous element (if it exists) has index (i-1), and its next element (if it exists) has index (i+1). Rank of Element: - The rank of an element in a list is its order in this list. It’s defined to be one more the index of that element. So, the first element is at rank 1, the second is at rank 2, and so on. Array List (Vector): - A list (or Sequence) that supports access to its elements by their indices is called an array-list (or vector). This index concept is used to specify where to insert a new element into a list, or where to remove and old element. © 2004 Goodrich, Tamassia Lists and Iterators 3

6. 1. 1 The Array List (Vector) ADT The Vector ADT extends the notion of array by storing a sequence of arbitrary objects An element can be accessed, inserted or removed by specifying its index (number of elements preceding it) An exception is thrown if an incorrect index is specified (e. g. negative index, or larger than current size) © 2004 Goodrich, Tamassia Main vector operations: n object get (integer i): returns the element of S at index i, without removing it, 0 ≤ i ≤ n-1, otherwise, an error condition occurs. n object set (integer i, object o): replace the element at index i with o and return the old element, 0 ≤ i ≤ n-1 n object add (integer i, object o): insert a new element o to have index i, 0≤i≤n n object remove (integer i): removes and returns the element at index i, 0 ≤ i ≤ n-1 Additional operations size() and is. Empty() Lists and Iterators 4

We do not insist that an array should be used to implement an array list, so that the element at index 0 is stored at index 0 in the array. The index definition offers us a way to refer to the “place” where an element is stored in a sequence, without having to worry about the exact implementation of that sequence. The index of an element may change whenever the sequence (array list) is updated, however, as we illustrate in the following example. © 2004 Goodrich, Tamassia Lists and Iterators 5

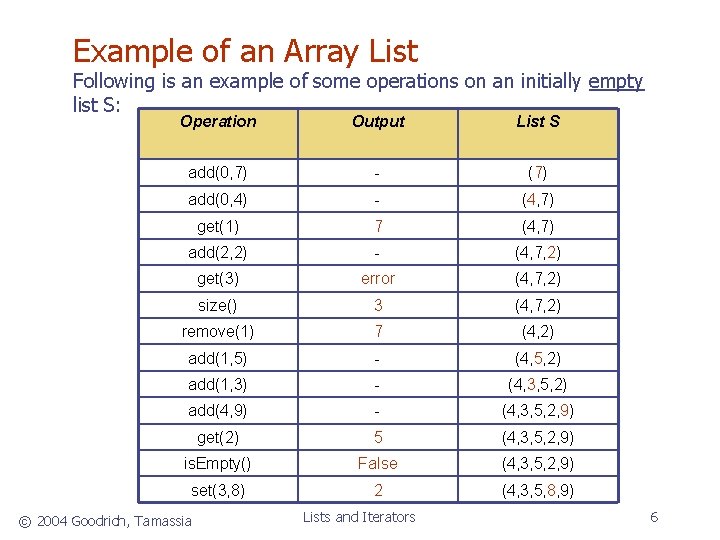
Example of an Array List Following is an example of some operations on an initially empty list S: Operation Output List S add(0, 7) - (7) add(0, 4) - (4, 7) get(1) 7 (4, 7) add(2, 2) - (4, 7, 2) get(3) error (4, 7, 2) size() 3 (4, 7, 2) remove(1) 7 (4, 2) add(1, 5) - (4, 5, 2) add(1, 3) - (4, 3, 5, 2) add(4, 9) - (4, 3, 5, 2, 9) get(2) 5 (4, 3, 5, 2, 9) is. Empty() False (4, 3, 5, 2, 9) set(3, 8) 2 (4, 3, 5, 8, 9) © 2004 Goodrich, Tamassia Lists and Iterators 6

Applications of Vectors Direct applications n Sorted collection of objects (elementary database) Indirect applications n n Auxiliary data structure for algorithms Component of other data structures © 2004 Goodrich, Tamassia Lists and Iterators 7

6. 1. 3 A Simple Array-based Implementation of Vector An obvious choice for implementing the array-list (vector) ADT is to use an array V , where V [i] stores (a reference to) the element with index i. Use an array V of size N, that is sufficiently large. A variable n keeps track of the size of the vector (number of elements stored). Operation get (i) is implemented in O(1) time by returning V [i] Array V 0 1 2 © 2004 Goodrich, Tamassia i Lists and Iterators n 8

Insertion In operation add(i, o), we need to make room for the new element by shifting forward the n i elements V [i], …, V [n 1] In the worst case (i = 0), this takes O(n) time V 0 1 2 i n 0 1 2 o i V V © 2004 Goodrich, Tamassia Lists and Iterators n 9

Insertion Algorithm add(i, o) for j = n-1, n-2, … , i do V [j+1] ← V [j] V [i] ← o n ← n+1 © 2004 Goodrich, Tamassia {make room for the new element} Lists and Iterators 10

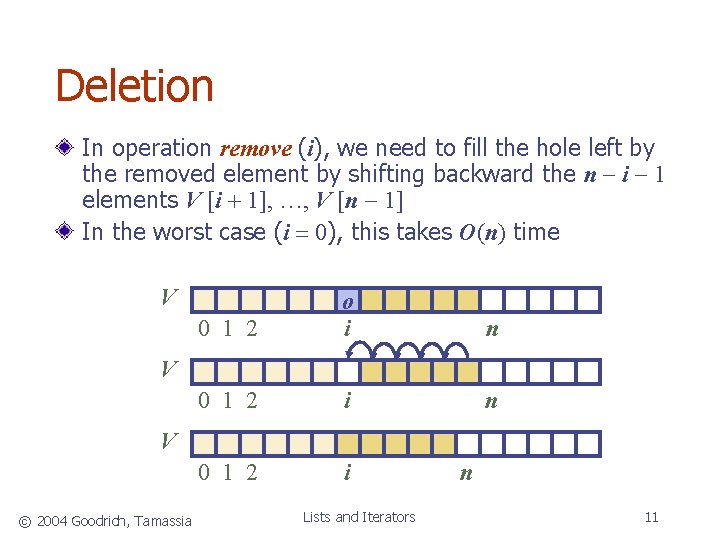
Deletion In operation remove (i), we need to fill the hole left by the removed element by shifting backward the n i 1 elements V [i + 1], …, V [n 1] In the worst case (i = 0), this takes O(n) time V 0 1 2 o i n 0 1 2 i V V © 2004 Goodrich, Tamassia Lists and Iterators n 11

Deletion Algorithm remove(i) e ← V [i] for j = i, i+1, …, n-2 do V [j] ← V [j+1] n ← n-1 return e © 2004 Goodrich, Tamassia {e is a temporary variable} {fill in the room of the removed element} Lists and Iterators 12

Performance of Array Implementation In the array-based implementation of a Vector ADT n The space used by the data structure is O(n) n size, is. Empty, get and set run in O(1) time n add and remove run in O(n) time (worst case, i = 0) n add(n, e) and remove(n-1) run in O(1) time (add or remove at the end of list) If we use the array in a circular fashion, add(0, e) and remove (0) run in O(1) time. In this implementation, we give up our rule that an element at index i is stored in the array at index i. © 2004 Goodrich, Tamassia Lists and Iterators 13

6. 1. 5 Extendable Array-based Vector In an add operation, when the array is full, instead of throwing an exception, we can replace the array with a larger one An illustration of the three steps for "growing" an extendable array: n n n (a) create new array B; (b) copy elements from A to B; (c) reassign reference A to the new array © 2004 Goodrich, Tamassia Lists and Iterators 14

6. 1. 5 Extendable Array-based Vector Algorithm push(o) if t = A. length 1 then B new array of size … for i 0 to t do B[i] A[i] A B t t+1 A[t] o © 2004 Goodrich, Tamassia Lists and Iterators 15

Comparison of the Strategies How large should the new array be? n incremental strategy: increase the size by a constant c n doubling strategy: double the size We compare the incremental strategy and the doubling strategy by analyzing the total time T(n) needed to perform a series of n push operations © 2004 Goodrich, Tamassia Lists and Iterators 16

Comparison of the Strategies We assume that we start with an empty stack represented by an array of size 1 We call amortized time of a push operation the average time taken by a push over the series of operations, i. e. , T(n)/n © 2004 Goodrich, Tamassia Lists and Iterators 17

Incremental Strategy Analysis We replace the array k = n/c times The total cost T(n) of a series of n push operations is proportional to n + 2(c + 2 c + 3 c + 4 c + … + kc) = n + 2 c(1 + 2 + 3 + … + k) = n + 2 c × k(k + 1)/2 = O(n+k 2) © 2004 Goodrich, Tamassia Lists and Iterators 18

Incremental Strategy Analysis Since c is a constant, T(n) = O(n+k 2) = O(n+(n/c)2) = O(n 2) The amortized time of 1 push is O(n 2)/n = O(n) © 2004 Goodrich, Tamassia Lists and Iterators 19

Doubling Strategy Analysis We replace the array k = log 2 n times geometric series The total time T(n) of a series of 2 n push operations is 4 proportional to 1 1 n + 2×(1 + 2 + 4 + 8 + …+ 2 k) = n + 2×(2 k + 1 1) = 3 n 2 = O(n) 8 The amortized time of 1 push is O(n)/n = O(1) © 2004 Goodrich, Tamassia Lists and Iterators 20