CHAPTER 6 LINEAR PROGRAMMING INTRODUCTION INPUTS Resource Raw

CHAPTER 6: LINEAR PROGRAMMING ¨ INTRODUCTION

¨ INPUTS: Resource: Raw material, Labour…and how much of each resource ¨ FACTORY: Production process: how much of each of the inputs per unit output. ¨ OUTPUTS: What products to manufacture. ¨ THE BUSINESS OBJECTIVE: To maximise profit, to minimise costs.

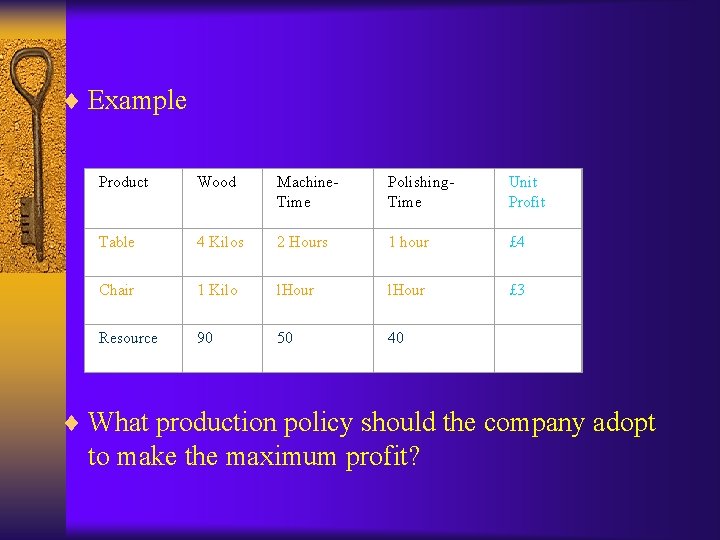
¨ Example Product Wood Machine. Time Polishing. Time Unit Profit Table 4 Kilos 2 Hours 1 hour £ 4 Chair 1 Kilo l. Hour £ 3 Resource 90 50 40 ¨ What production policy should the company adopt to make the maximum profit?

¨ OUTPUTS: Tables and Chairs ¨ INPUTS: The following resources with the availability as given: – WOOD: 90 Kilograms available per week. – MACHINE-TIME: 50 hours available per week. – POLISHING-TIME: 40 hours available per week. ¨ FACTORY: – One Table requires 4 Kilograms of Wood, 2 hours of Machine-Time and 1 hour of Polishing-Time. – One Chair requires 1 Kilograms of Wood, 1 hour of Machine-Time and 1 hour of Polishing-Time. ¨ BUSINESS OBJECTIVE: How much is Tables and Chairs to be manufactured that leads to maximum profits.

¨ SOLVING THIS PROBLEM – Graphical Solution an Intuitive Approach • Stage 1: The set of all possible production plans that meet all the factory input constraints are evaluated. • Stage 2: From the set of all possible production plans the particular production plan that meets the business objective is found.

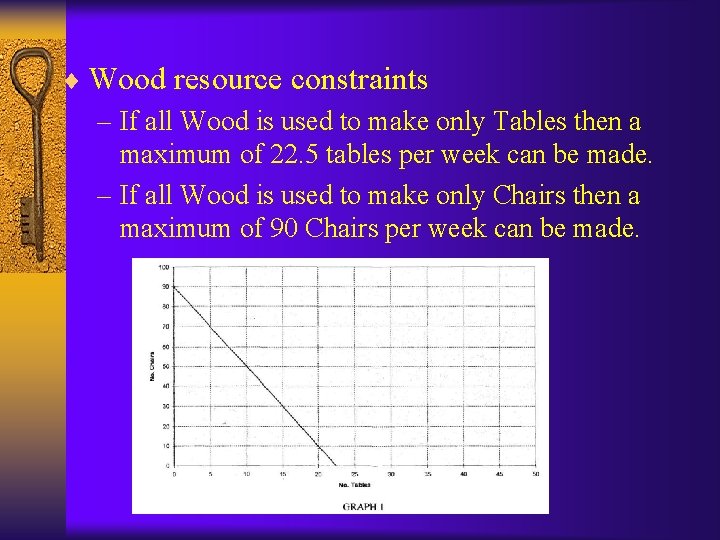
¨ Wood resource constraints – If all Wood is used to make only Tables then a maximum of 22. 5 tables per week can be made. – If all Wood is used to make only Chairs then a maximum of 90 Chairs per week can be made.

– RESULT 1 : Any point that lies on a constraint line uses the exact amount of the resource that is available. – RESULT 2: Any point under the constraint line uses less of the resource that is available. – RESULT 3 : Any point above the constraint line uses more of the resource than is available.

¨ Machine-Time resource constraint • Using all the Machine-Time to make only Tables would enable a maximum of 25 Tables per week to be made. • Using all the Machine-Time to make only Chairs then a maximum of 50 Chairs per week could be made.

¨ Polishing-Time resource constraints – If all the Polishing-Time is used to make only Tables then 40 Tables per week could be made. – If all the Polishing-Time is used to make only Chairs the 40 Chairs per week could be made. Feasible Region: OABCD

¨ Stage 2 – Starting point: (15, 15) • Profit = £(4*15 + 3*15) = £ 105 – Move vertically upwards: (15, 20) • Profit = £(4*15+ 3*20) = £ 120 – Move down the Machine-Time line: (16, 18) • Profit = £(4*16+ 3*18) = £ 118 – Move up the Machine-Time line: (14, 22) • Profit = £(4*14+ 3*22) = £ 122

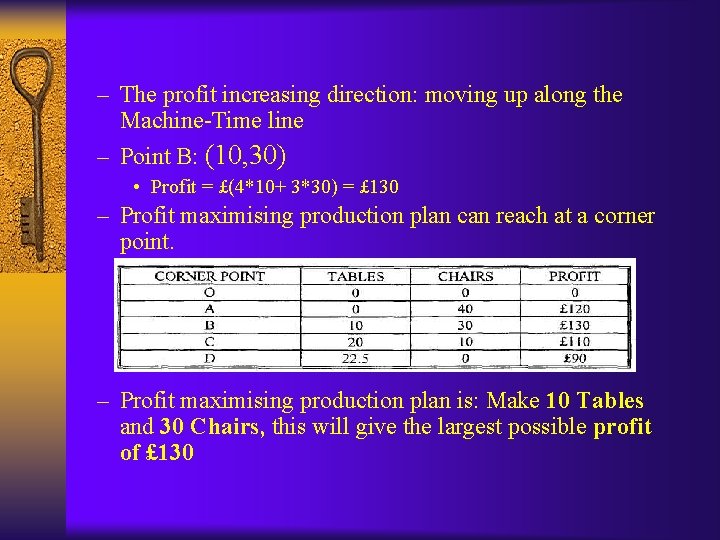
– The profit increasing direction: moving up along the Machine-Time line – Point B: (10, 30) • Profit = £(4*10+ 3*30) = £ 130 – Profit maximising production plan can reach at a corner point. – Profit maximising production plan is: Make 10 Tables and 30 Chairs, this will give the largest possible profit of £ 130

¨ WHAT IS LINEAR PROGRAMMING? – To find the particular production plan that maximises a linear profit function, when production is constrained by a set of linear constraints.