Chapter 6 Linear Equations Example 1 solve the

Chapter 6 Linear Equations

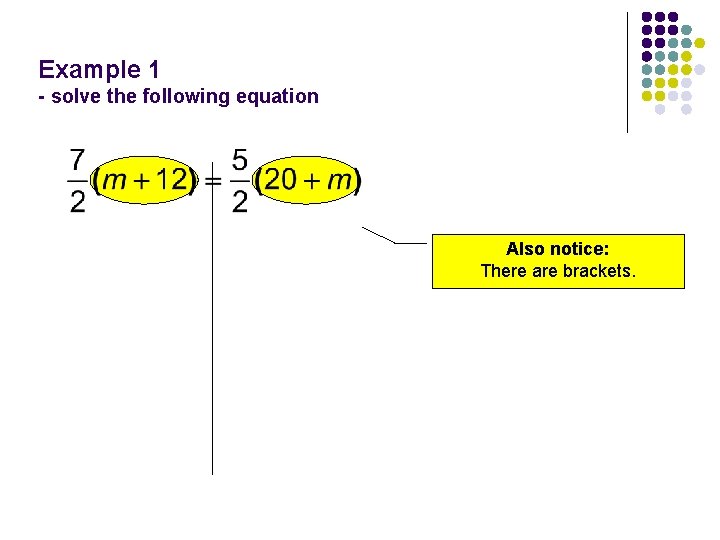
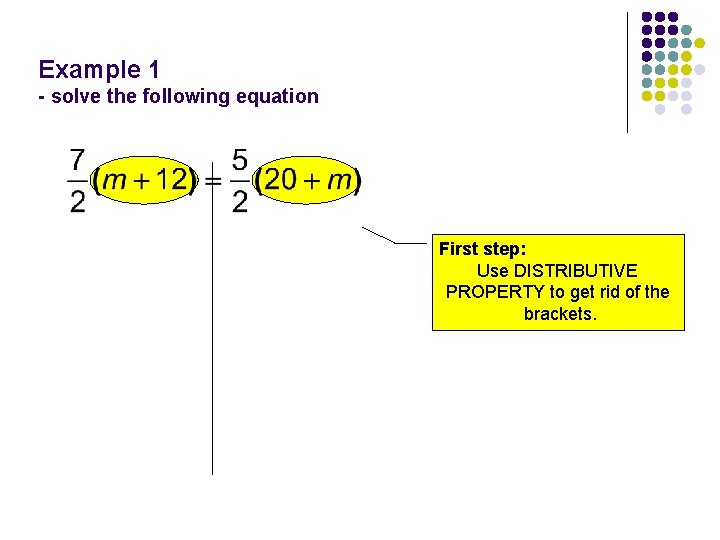
Example 1 - solve the following equation

Example 1 - solve the following equation

Example 1 - solve the following equation Notice: There is a variable in the expressions on BOTH sides of the equal sign.

Example 1 - solve the following equation Notice: There is a variable in the expressions on BOTH sides of the equal sign. We will need to get all variables to one side.

Example 1 - solve the following equation Also notice: There are brackets.

Example 1 - solve the following equation First step: Use DISTRIBUTIVE PROPERTY to get rid of the brackets.

Example 1 - solve the following equation First step: Use DISTRIBUTIVE PROPERTY to get rid of the brackets.

Example 1 - solve the following equation Change 5/2 into decimal… 2. 5 Change 7/2 into decimal… 3. 5

Example 1 - solve the following equation 3. 5(m + 12) = 2. 5(20 + m) Change 5/2 into decimal… 2. 5 Change 7/2 into decimal… 3. 5

Example 1 - solve the following equation 3. 5(m + 12) = 2. 5(20 + m) Use DISTRIBUTIVE PROPERTY to get rid of the brackets.

Example 1 - solve the following equation 3. 5(m + 12) = 2. 5(20 + m) 3. 5 m + 42 = 50 + 2. 5 m First step: Use DISTRIBUTIVE PROPERTY to get rid of the brackets.

Example 1 - solve the following equation 3. 5(m + 12) = 2. 5(20 + m) 3. 5 m + 42 = 50 + 2. 5 m Second step: Collect all of the variables onto ONE side of the equation.

Example 1 - solve the following equation 3. 5(m + 12) = 2. 5(20 + m) 3. 5 m + 42 = 50 + 2. 5 m -2. 5 m Second step: Collect all of the variables onto ONE side of the equation.

Example 1 - solve the following equation 3. 5(m + 12) = 2. 5(20 + m) 3. 5 m + 42 = 50 + 2. 5 m -2. 5 m 1 m + 42 = 50

Example 1 - solve the following equation 3. 5(m + 12) = 2. 5(20 + m) 3. 5 m + 42 = 50 + 2. 5 m -2. 5 m 1 m + 42 = 50 Third step: Now solve as usual to isolate the variable on one side of the equation. “Undo” the equation using “reverse BEDMAS. ”

Example 1 - solve the following equation 3. 5(m + 12) = 2. 5(20 + m) 3. 5 m + 42 = 50 + 2. 5 m -2. 5 m 1 m + 42 = 50 -42

Example 1 - solve the following equation 3. 5(m + 12) = 2. 5(20 + m) 3. 5 m + 42 = 50 + 2. 5 m -2. 5 m 1 m + 42 = 50 -42 1 m = 8

Example 1 - solve the following equation 3. 5(m + 12) = 2. 5(20 + m) 3. 5 m + 42 = 50 + 2. 5 m -2. 5 m 1 m + 42 = 50 -42 1 m = 8 So, m = 8

Example 1 - solve the following equation 3. 5(m + 12) = 2. 5(20 + m) 3. 5 m + 42 = 50 + 2. 5 m -2. 5 m 1 m + 42 = 50 -42 1 m = 8 Check your solution! 7(m + 12) = 5(20 + m) 2 2 3. 5(8 + 12) = 2. 5(20 + 8) 3. 5(20) = 2. 5(28) 70 = 70

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same?

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Our goal: Find the TIME, in minutes, when Plan A equals Plan B.

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Choose a variable.

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Choose a variable. Let t minutes represent the time for calls.

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Find an expression for Plan A.

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Plan A • You pay only for >120 min.

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Plan A • You pay only for >120 min. • So time you pay, in minutes, is (t - 120)

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Plan A • You pay only for >120 min. • So time you pay, in minutes, is (t - 120) • Additional minutes cost $0. 75.

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Plan A • You pay only for >120 min. • So time you pay, in minutes, is (t - 120) • Additional minutes cost $0. 75. • So, the cost in dollars is 0. 75(t - 120)

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Now find an expression for Plan B.

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Plan B • You pay only for >30 min.

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Plan B • You pay only for >30 min. • So time you pay, in minutes, is (t - 30)

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Plan B • You pay only for >30 min. • So time you pay, in minutes, is (t - 30) • Additional minutes cost $0. 25.

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Plan B • You pay only for >30 min. • So time you pay, in minutes, is (t - 30) • Additional minutes cost $0. 25. • So, the cost in dollars is 0. 25(t - 30)

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Now, when is t equal for Plan A and Plan B?

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Set the expression for Plan A equal to the expression for Plan B.

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Plan A = Plan B

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Model the problem with an equation Plan A = Plan B 0. 75(t - 120)= 0. 25(t - 30)

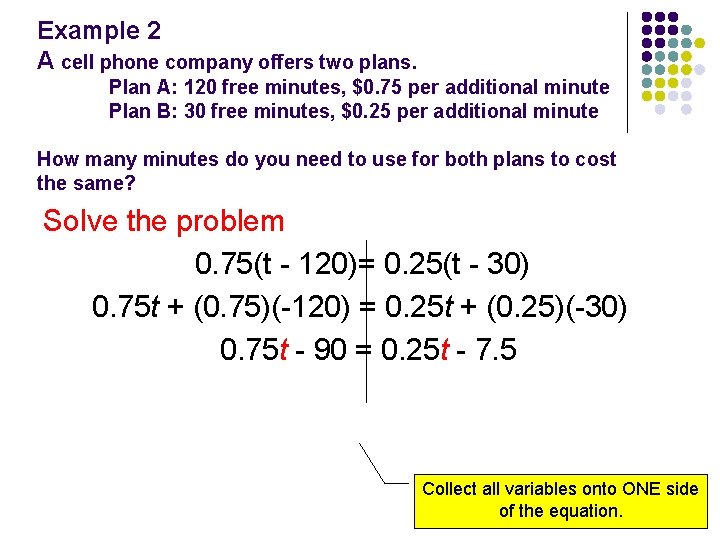
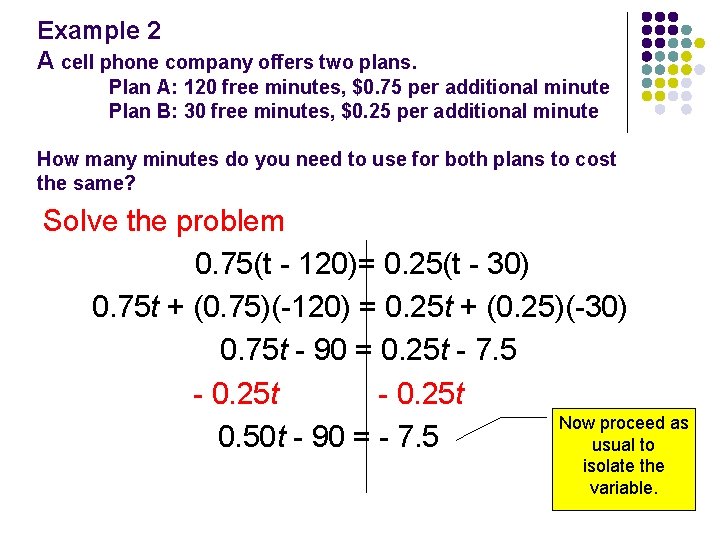
Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Solve the problem

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Solve the problem 0. 75(t - 120)= 0. 25(t - 30)

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Solve the problem 0. 75(t - 120)= 0. 25(t - 30) Use the DISTRIBUTIVE PROPERTY to get rid of brackets

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Solve the problem 0. 75(t - 120)= 0. 25(t - 30) Use the DISTRIBUTIVE PROPERTY to get rid of brackets

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Solve the problem 0. 75(t - 120)= 0. 25(t - 30) 0. 75 t + (0. 75)(-120) = 0. 25 t + (0. 25)(-30) Use the DISTRIBUTIVE PROPERTY to get rid of brackets

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Solve the problem 0. 75(t - 120)= 0. 25(t - 30) 0. 75 t + (0. 75)(-120) = 0. 25 t + (0. 25)(-30) Simplify where possible.

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Solve the problem 0. 75(t - 120)= 0. 25(t - 30) 0. 75 t + (0. 75)(-120) = 0. 25 t + (0. 25)(-30) 0. 75 t - 90 = 0. 25 t - 7. 5 Simplify where possible.

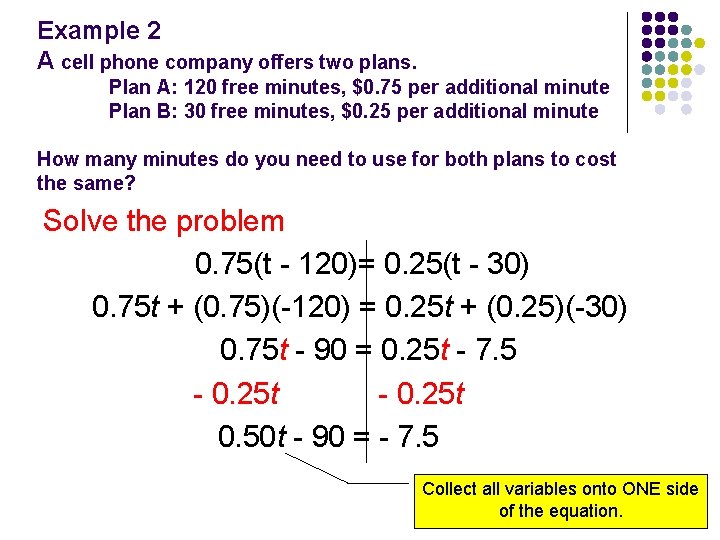
Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Solve the problem 0. 75(t - 120)= 0. 25(t - 30) 0. 75 t + (0. 75)(-120) = 0. 25 t + (0. 25)(-30) 0. 75 t - 90 = 0. 25 t - 7. 5 Collect all variables onto ONE side of the equation.

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Solve the problem 0. 75(t - 120)= 0. 25(t - 30) 0. 75 t + (0. 75)(-120) = 0. 25 t + (0. 25)(-30) 0. 75 t - 90 = 0. 25 t - 7. 5 - 0. 25 t Collect all variables onto ONE side of the equation.

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Solve the problem 0. 75(t - 120)= 0. 25(t - 30) 0. 75 t + (0. 75)(-120) = 0. 25 t + (0. 25)(-30) 0. 75 t - 90 = 0. 25 t - 7. 5 - 0. 25 t 0. 50 t - 90 = - 7. 5 Collect all variables onto ONE side of the equation.

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Solve the problem 0. 75(t - 120)= 0. 25(t - 30) 0. 75 t + (0. 75)(-120) = 0. 25 t + (0. 25)(-30) 0. 75 t - 90 = 0. 25 t - 7. 5 - 0. 25 t Now proceed as 0. 50 t - 90 = - 7. 5 usual to isolate the variable.

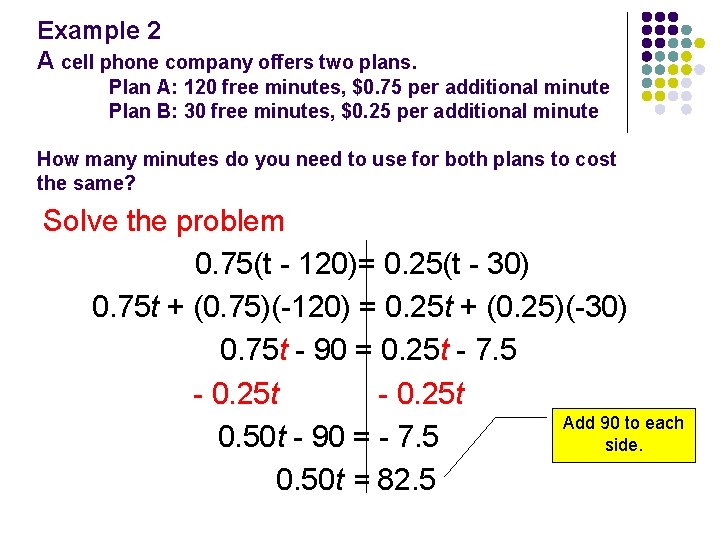
Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Solve the problem 0. 75(t - 120)= 0. 25(t - 30) 0. 75 t + (0. 75)(-120) = 0. 25 t + (0. 25)(-30) 0. 75 t - 90 = 0. 25 t - 7. 5 - 0. 25 t Add 90 to each 0. 50 t - 90 = - 7. 5 side. 0. 50 t = 82. 5

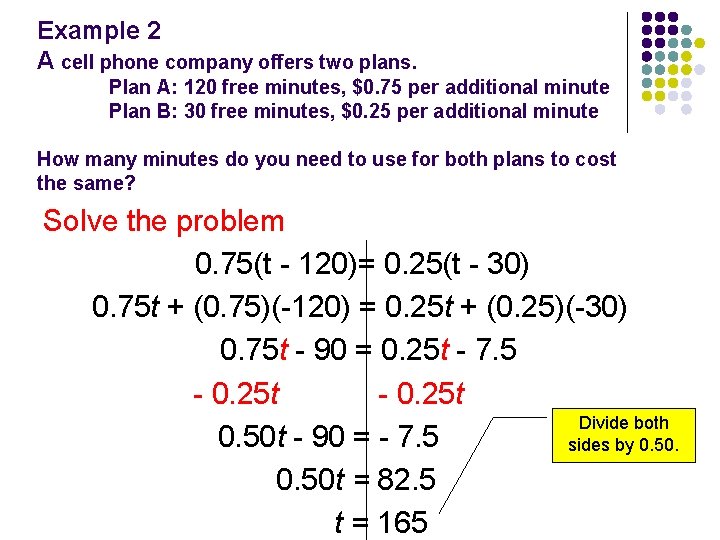
Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Solve the problem 0. 75(t - 120)= 0. 25(t - 30) 0. 75 t + (0. 75)(-120) = 0. 25 t + (0. 25)(-30) 0. 75 t - 90 = 0. 25 t - 7. 5 - 0. 25 t Divide both 0. 50 t - 90 = - 7. 5 sides by 0. 50 t = 82. 5 t = 165

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Solve the problem 0. 75(t - 120)= 0. 25(t - 30) 0. 75 t + (0. 75)(-120) = 0. 25 t + (0. 25)(-30) 0. 75 t - 90 = 0. 25 t - 7. 5 - 0. 25 t The cost is the same for both 0. 50 t - 90 = - 7. 5 plans when you use 165 0. 50 t = 82. 5 minutes! t = 165

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Verify the solution.

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Verify the solution. Does t = 165? Plan A: 165 - 120, or 45 minutes

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Verify the solution Plan A: 165 - 120, or 45 minutes The cost is: 45 x $0. 75 = $33. 75

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Verify the solution Plan A: 165 - 120, or 45 minutes The cost is: 45 x $0. 75 = $33. 75 Plan B: 165 - 30, or 135 minutes

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Verify the solution Plan A: 165 - 120, or 45 minutes The cost is: 45 x $0. 75 = $33. 75 Plan B: 165 - 30, or 135 minutes The cost is: 135 x $0. 25 = $33. 75

Example 2 A cell phone company offers two plans. Plan A: 120 free minutes, $0. 75 per additional minute Plan B: 30 free minutes, $0. 25 per additional minute How many minutes do you need to use for both plans to cost the same? Verify the solution Plan A: 165 - 120, or 45 minutes The cost is: 45 x $0. 75 = $33. 75 Plan B: 165 - 30, or 135 minutes The cost is: 135 x $0. 25 = $33. 75 The costs are equal, so the solution is correct.