Chapter 6 INVENTORY MANAGEMENT Yabibal A Lecture Outline

Chapter 6 INVENTORY MANAGEMENT Yabibal A.

Lecture Outline Elements of Inventory Management Inventory Control Systems Economic Order Quantity Models Quantity Discounts Reorder Point Order Quantity for a Periodic Inventory System

What Is Inventory? Stock of items kept to meet future demand Purpose of inventory management how many units to order when to order

Reasons for Inventory and Bullwhip Effect Bullwhip effect demand information is distorted as it moves away from the end-use customer higher safety stock inventories are stored to compensate Seasonal or cyclical demand Inventory provides independence from vendors Take advantage of price discounts Inventory provides independence between stages and avoids work stoppages

Inventory and Quality Management in the Supply Chain Customers usually perceive quality service as availability of goods they want when they want them Inventory must be sufficient to provide highquality customer service in QM

Types of Inventory Raw materials Work-in-process (partially completed) products (WIP) Finished Goods Purchased parts and supplies Items being transported Tools and equipment

Two Forms of Demand § Dependent § Demand for items used to produce final products § Tires stored at a Goodyear plant are an example of a dependent demand item § Independent § Demand for items used by external customers § Cars, appliances, computers, and houses are examples of independent demand inventory

Inventory Costs § Carrying cost § cost of holding an item in inventory § Ordering cost § cost of replenishing inventory § Shortage cost § temporary or permanent loss of sales when demand cannot be met

Inventory Control Systems § ABC Classification § Continuous system (fixedorder-quantity) § constant amount ordered when inventory declines to predetermined level § Periodic system (fixed-timeperiod) § order placed for variable amount after fixed passage of time

ABC Classification Class A 5 – 15 % of units 70 – 80 % of value Class B 30 % of units 15 % of value Class C 50 – 60 % of units 5 – 10 % of value

ABC Classification: Example PART 1 2 3 4 5 6 7 8 9 10 UNIT COST ANNUAL USAGE $ 60 350 30 80 30 20 10 320 510 20 90 40 130 60 100 180 170 50 60 120

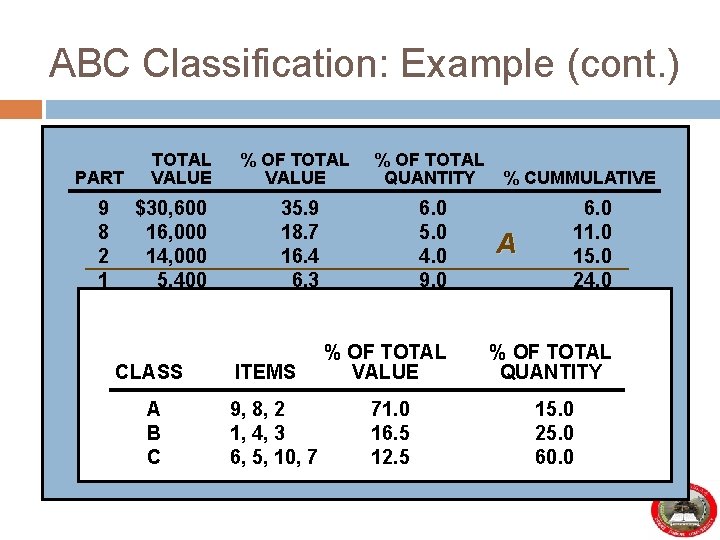
ABC Classification: Example (cont. ) PART TOTAL PART VALUE 9 $30, 600 1 8 16, 000 2 2 14, 000 3 1 5, 400 4 4 4, 800 5 3 3, 900 6 3, 600 6 5 CLASS 3, 000 7 10 A 2, 400 8 7 1, 700 B 9 $85, 400 C 10 % OF TOTAL UNIT ANNUAL USAGE VALUECOSTQUANTITY % CUMMULATIVE 35. 9 6. 0 $ 60 18. 7 5. 0 350 16. 4 4. 0 30 6. 3 9. 0 5. 680 6. 0 4. 630 10. 0 % OF TOTAL 4. 220 18. 0 ITEMS 3. 5 10 VALUE 13. 0 9, 8, 2 2. 8 320 71. 012. 0 1, 4, 3 2. 0 16. 517. 0 510 6, 5, 10, 7 20 12. 5 6. 0 90 11. 0 40 A 15. 0 130 24. 0 30. 0 B 60 100 40. 0 % OF TOTAL 58. 0 180 QUANTITY 71. 0 170 C 50 15. 083. 0 100. 0 25. 0 60 60. 0 120 Example 10. 1

Continuous Review: Economic Order Quantity (EOQ) Models EOQ optimal order quantity that will minimize total inventory costs Basic EOQ model Production quantity model

Assumptions of Basic EOQ Model Assuming Continuous REVIEW § Demand is known with certainty and is constant over time § No shortages are allowed § Lead time for the receipt of orders is constant § Order quantity is received all at once

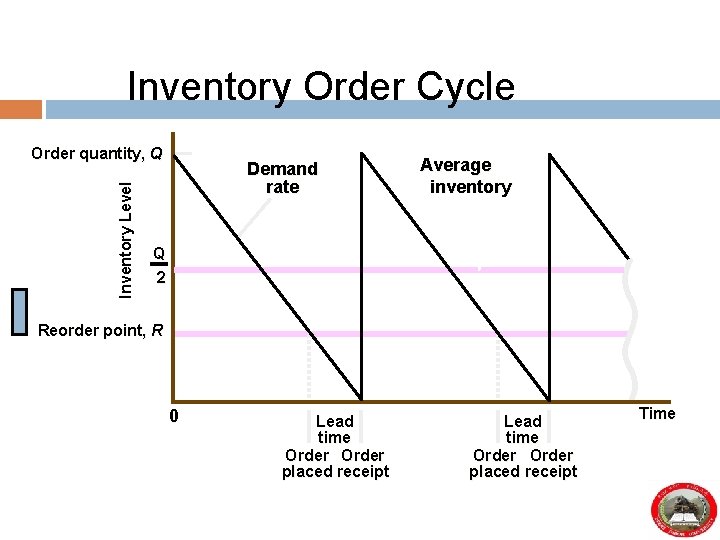
Inventory Order Cycle Inventory Level Order quantity, Q Demand rate Average inventory Q 2 Reorder point, R 0 Lead time Order placed receipt Time

EOQ Cost Model Co - cost of placing order Cc - annual per-unit carrying cost D - annual demand Q - order quantity Annual ordering cost = Co D Q Annual carrying cost = Cc Q 2 Co D Cc Q Total cost = + Q 2

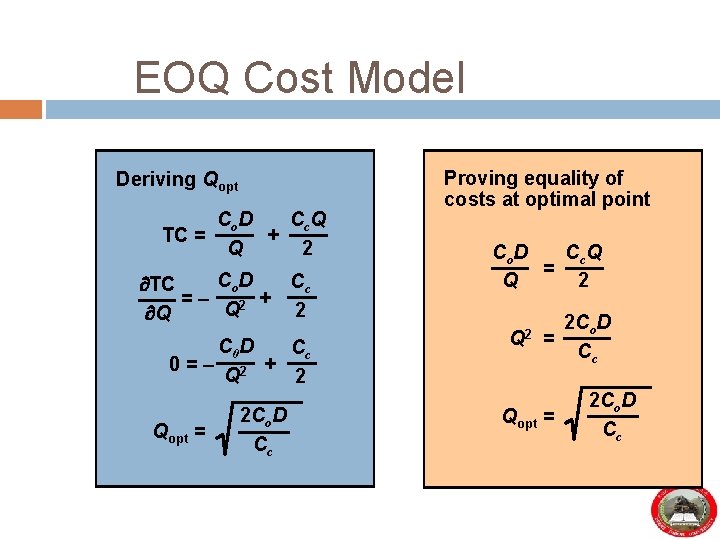
EOQ Cost Model Deriving Qopt Co D Cc Q TC = + Q 2 Co D Cc TC =– 2 + Q 2 Q C 0 D Cc 0=– 2 + Q 2 Qopt = 2 Co. D Cc Proving equality of costs at optimal point Co D Cc Q = Q 2 2 Co. D = Cc Qopt = 2 Co. D Cc

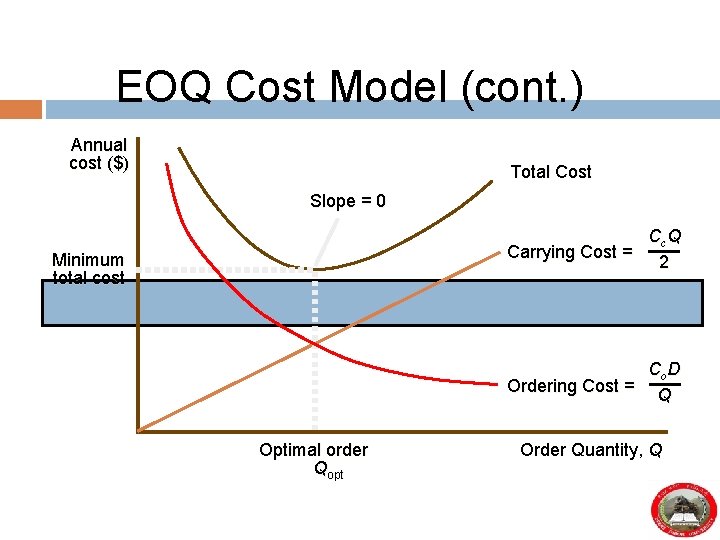
EOQ Cost Model (cont. ) Annual cost ($) Total Cost Slope = 0 Cc. Q Carrying Cost = 2 Minimum total cost Co D Ordering Cost = Q Optimal order Qopt Order Quantity, Q

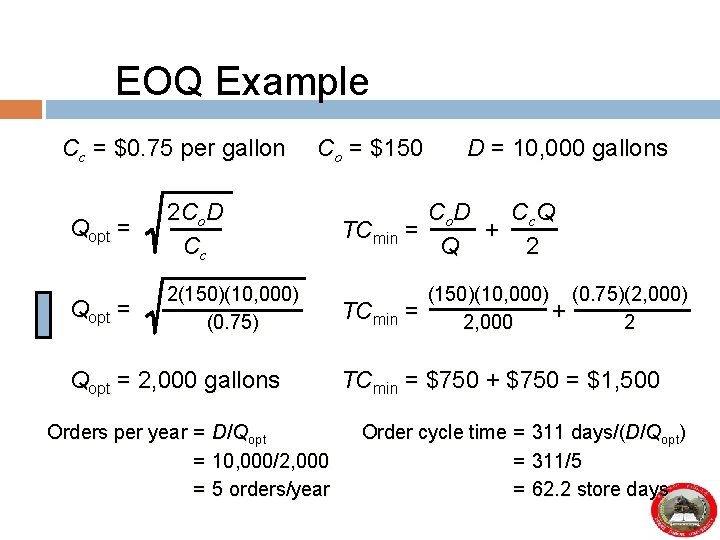
EOQ Example Cc = $0. 75 per gallon Qopt = 2 Co. D Cc Qopt = 2(150)(10, 000) (0. 75) Co = $150 Qopt = 2, 000 gallons Orders per year = = = D/Qopt 10, 000/2, 000 5 orders/year D = 10, 000 gallons Co. D Cc Q TCmin = + Q 2 TCmin = (150)(10, 000) (0. 75)(2, 000) + 2, 000 2 TCmin = $750 + $750 = $1, 500 Order cycle time = = = 311 days/(D/Qopt) 311/5 62. 2 store days

Production Quantity Model (Continuous Review with noninstantaneous receipt) An EOQ Model in which an order is received gradually, as inventory is simultaneously being depleted AKA non-instantaneous receipt model assumption that Q is received all at once is relaxed p - daily rate at which an order is received over time, a. k. a. production rate d - daily rate at which inventory is demanded

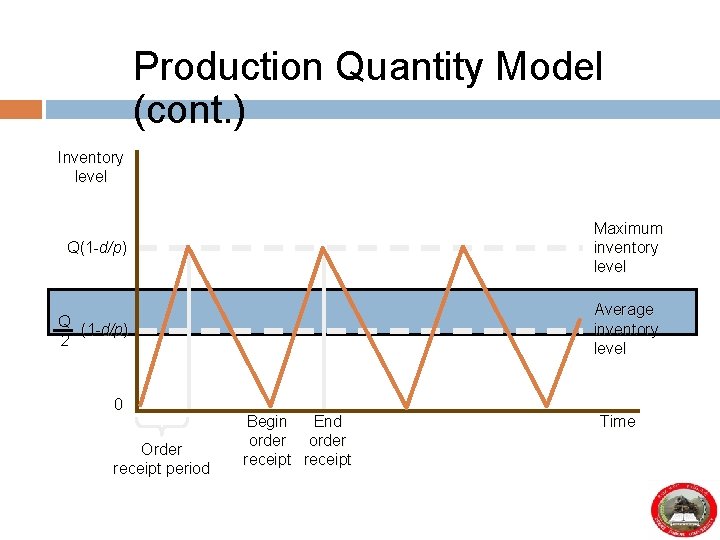
Production Quantity Model (cont. ) Inventory level Q(1 -d/p) Maximum inventory level Q (1 -d/p) 2 Average inventory level 0 Order receipt period Begin End order receipt Time

Production Quantity Model (cont. ) p = production rate Maximum inventory level = Q - d = demand rate Q d p =Q 1 - d p Q d Average inventory level = 1 p 2 Co D Cc Q d TC = Q + 2 1 - p Qopt = 2 Co. D d Cc 1 p

Production Quantity Model: Example Cc = $0. 75 per gallon Co = $150 d = 10, 000/311 = 32. 2 gallons per day 2 Co D Qopt = Cc 1 - d p D = 10, 000 gallons p = 150 gallons per day 2(150)(10, 000) = Co D Cc Q d TC = Q + 2 1 - p 32. 2 0. 75 1 150 = 2, 256. 8 gallons = $1, 329 2, 256. 8 Q Production run = = = 15. 05 days per order p 150

Production Quantity Model: Example (cont. ) Number of production runs = 10, 000 D = = 4. 43 runs/year 2, 256. 8 Q Maximum inventory level = Q 1 - d p = 2, 256. 8 1 - = 1, 772 gallons 32. 2 150

Solution of EOQ Models with Excel

Solution of EOQ Models with Excel (Con’t)

Solution of EOQ Models with OM Tools

Continuous Review EOQ with Quantity Discounts Price per unit decreases as order quantity increases We have to add annual cost Co. D Cc Q TC = Q + 2 + PD where P = per unit price of the item D = annual demand

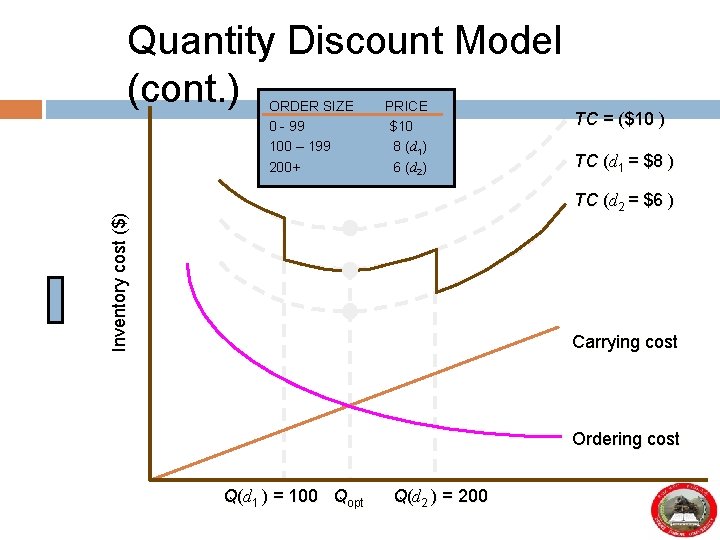
Quantity Discount Model (cont. ) ORDER SIZE 0 - 99 100 – 199 200+ PRICE $10 8 (d 1) 6 (d 2) TC = ($10 ) TC (d 1 = $8 ) Inventory cost ($) TC (d 2 = $6 ) Carrying cost Ordering cost Q(d 1 ) = 100 Qopt Q(d 2 ) = 200

Quantity Discount: Example QUANTITY PRICE 1 - 49 50 - 89 90+ $1, 400 1, 100 900 Qopt = For Q = 72. 5 For Q = 90 2 Co D = Cc Co = $2, 500 Cc = $190 per TV D = 200 TVs per year 2(2500)(200) = 72. 5 TVs 190 Cc. Qopt Co D TC = + + PD = $233, 784 2 Qopt Cc Q Co D TC = + + PD = $194, 105 2 Q

Quantity-Discount Model Solution with Excel

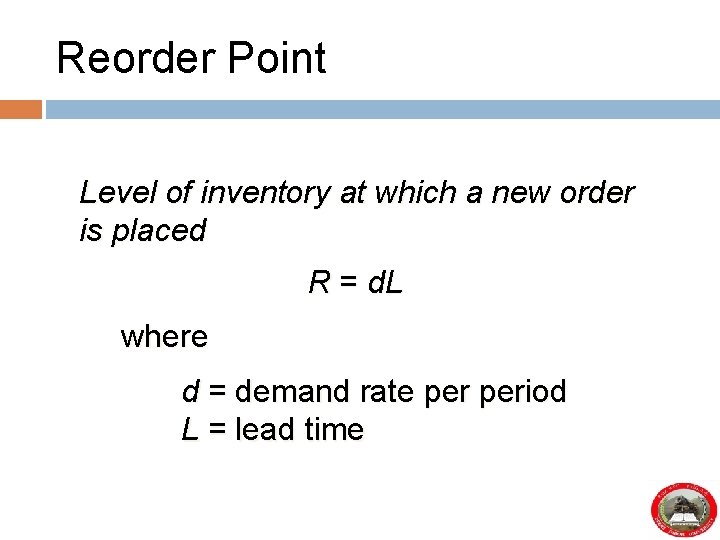
Reorder Point Level of inventory at which a new order is placed R = d. L where d = demand rate period L = lead time

Reorder Point: Example Demand = 10, 000 gallons/year Store is open 311 days/year Daily demand = 10, 000 / 311 = 32. 154 gallons/day Lead time = L = 10 days R = d. L = (32. 154)(10) = 321. 54 gallons

Safety Stocks § Safety stock § A buffer that is added to on-hand inventory during lead time § Stockout § An inventory shortage § Service level § The probability that the inventory available during lead time will meet demand

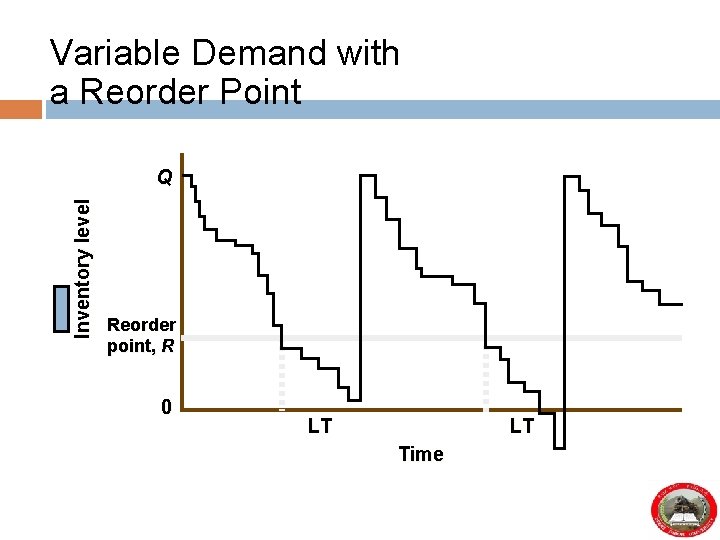
Variable Demand with a Reorder Point Inventory level Q Reorder point, R 0 LT LT Time

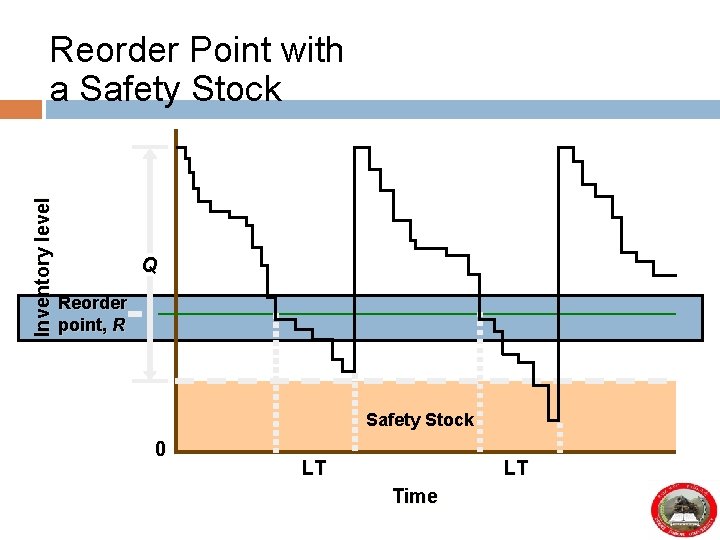
Inventory level Reorder Point with a Safety Stock Q Reorder point, R Safety Stock 0 LT LT Time

Reorder Point With Variable Demand R = d. L + z d L where d = average daily demand L = lead time d = the standard deviation of daily demand z = number of standard deviations corresponding to the service level probability z d L = safety stock

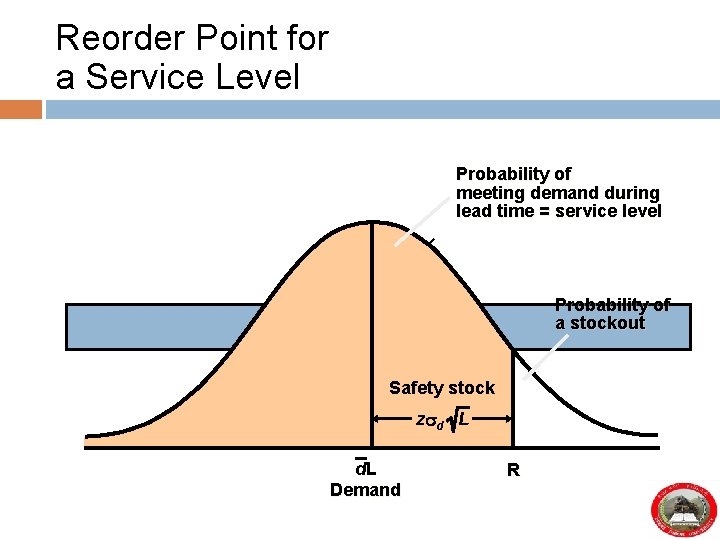
Reorder Point for a Service Level Probability of meeting demand during lead time = service level Probability of a stockout Safety stock z d L d. L Demand R

Reorder Point for Variable Demand The paint store wants a reorder point with a 95% service level and a 5% stockout probability d = 30 gallons per day L = 10 days d = 5 gallons per day For a 95% service level, z = 1. 65 R = d. L + z d L Safety stock = z d L = 30(10) + (1. 65)(5)( 10) = 326. 1 gallons = 26. 1 gallons

Determining Reorder Point with Excel

ANOTHER Control System: Order Quantity for a Periodic Inventory System Q = d(tb + L) + z d tb + L - I where d tb L d z d = average demand rate = the fixed time between orders = lead time = standard deviation of demand tb + L = safety stock I = inventory level

Periodic Inventory System

Fixed-Period Model with Variable Demand d = 6 packages per day d = 1. 2 packages tb = 60 days L = 5 days I = 8 packages z = 1. 65 (for a 95% service level) Q = d(tb + L) + z d tb + L - I = (6)(60 + 5) + (1. 65)(1. 2) = 397. 96 packages 60 + 5 - 8

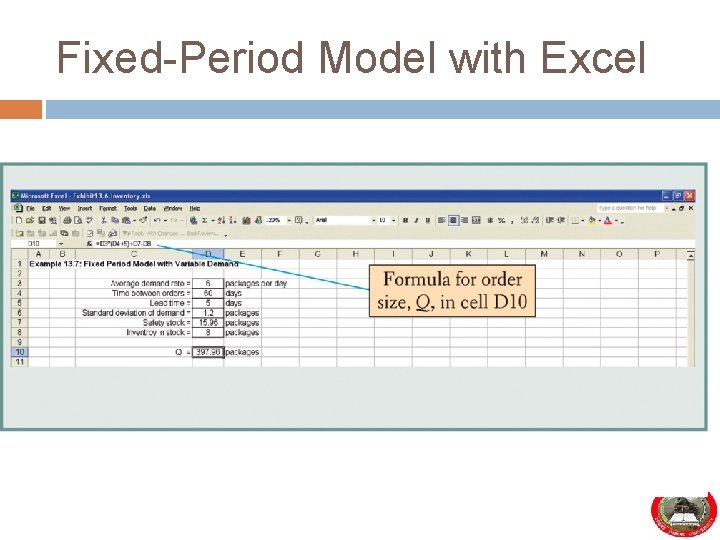
Fixed-Period Model with Excel

Thank you! Questions?