Chapter 6 Introduction to arrays What is an

Chapter 6 Introduction to arrays

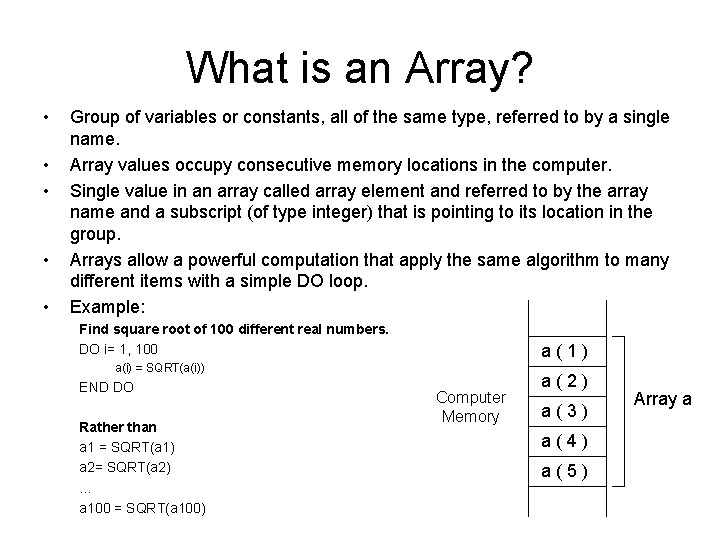
What is an Array? • • • Group of variables or constants, all of the same type, referred to by a single name. Array values occupy consecutive memory locations in the computer. Single value in an array called array element and referred to by the array name and a subscript (of type integer) that is pointing to its location in the group. Arrays allow a powerful computation that apply the same algorithm to many different items with a simple DO loop. Example: Find square root of 100 different real numbers. DO i= 1, 100 a(1) a(i) = SQRT(a(i)) END DO Rather than a 1 = SQRT(a 1) a 2= SQRT(a 2) … a 100 = SQRT(a 100) Computer Memory a(2) a(3) a(4) a(5) Array a

Arrays • Arrays can be multi-dimensions. • Number of subscripts called rank. • Extent of array in one dimension is the number of values in that given dimension of the array. • Shape of the array is the combination of its rank and the extent in each dimension. • Size of array is the total number of elements in all dimensions.

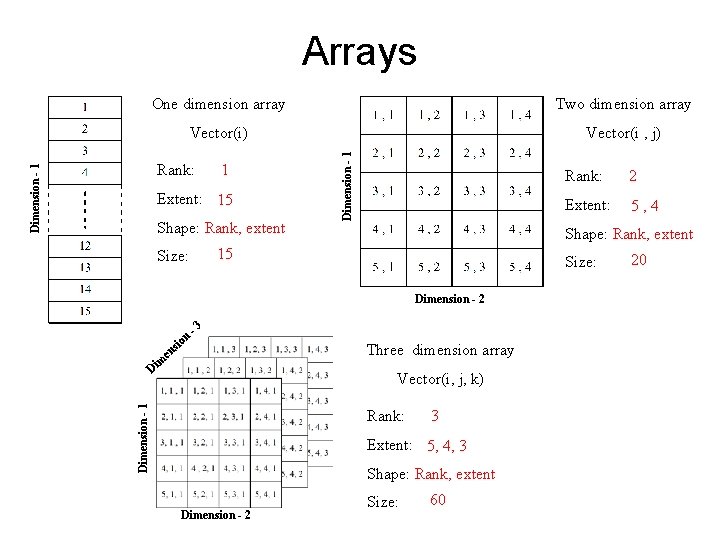
Arrays Two dimension array Vector(i) Vector(i , j) Dimension - 1 Rank: 1 Extent: 15 Shape: Rank, extent Dimension - 1 One dimension array en -3 m Di Three dimension array Dimension - 1 Vector(i, j, k) Rank: 3 Extent: 5, 4, 3 Shape: Rank, extent Dimension - 2 Extent: 5, 4 Size: Dimension - 2 n sio 2 Shape: Rank, extent 15 Size: Rank: Size: 60 20

Declaring Arrays • Define type and size REAL, DIMENSION(16) : : voltage INTEGER, DIMENSION(5, 6): : matrix, values CHARACTER(len=20), DIMENSION(50) : : last_name Find rank, extent, shape and size of above arrays. • Array constant (/ 3, 4, 5, 1, 3/)

Array example • Declares an array that stores the student ID of all students in the class. (43 students) INTEGER, DIMENSION(43) : : student. ID • Make a WRITE statement that makes the program display the first student in the class. WRITE(*, *) ‘ ID of first student: ’, student. ID(1) • Make a WRITE statement that makes the program display the student number 25 in the list. WRITE(*, *) ‘ ID of 25 th student: ’, student. ID(25)

Array example • • • Make two arrays that represent a building that consists of 7 floors. Each floor has 15 rooms. First array values indicates if the room is occupied or not. (True or False) The second array indicates how many persons in the room in case it is occupied. (Integer) LOGICAL, DIMENSION (7, 15) : : occupied INTEGER, DIMENSION (7, 15) : : persons • Please, write to the customer if room number 9 in the 6 th floor is occupied or not. WRITE(*, *) ‘Is room 9 in floor 6 occupied ? ’, occupid(6, 9) • Please, write how many persons in room 2 in the 7 th floor. WRITE(*, *) ‘persons in room 2 at floor 7 are: ’, persons(7, 2)

Using array elements in FORTRAN • Each element in the array is treated as any regular FORTRAN variable. • FORTRAN statements can access its values, assign values and make operations on them. • Back to student ID example: INTEGER, DIMENSION(43) : : student. ID(5)=999999 IF (student. ID(5)==999999) student. ID(4)=888888 student. ID(6) = MAX(student. ID(4), student. ID(5)) WRITE(*, *) ‘ ID of sixth student: ’, student. ID(6)

Initialization of array elements • Un-initialized array INTEGER, DIMENSION(10) : : j WRITE (*, *) ‘ j(1) = ’, j(1) • Initialization with assignment statement REAL, DIMENSION(10) : : array 1 DO I = 1, 10 array 1(i) = REAL(i) END DO • Initialization with assignment using array constructor REAL, DIMENSION(10) : : array 1 = (/1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. , 10. /) • Possible to assign one value to all array elements. REAL, DIMENSION(10) : : array 1 = 0.

Example-1 PROGRAM squares IMPLICIT NONE INTEGER : : i INTEGER, DIMENSION(10) : : number, square DO i=1, 10 number(i)=i square(i)=number(i)**2 END DO DO i=1, 10 WRITE(*, *) number(i), ' END DO END PROGRAM ', square(i)

Initialization of array elements • Named constants in array declaration INTEGER, PARAMETER : : max_size=1000 INTEGER, DIMENSION(max_size) : : array 1 REAL, DIMENSION(2*max_size) : : array 2 Do i = 1, max_size array 2(i) = array 1(i) * 2. 0 / 3. 0 END DO

Initialization of array elements • Initializing with READ statement INTEGER, DIMENSION(5) : : array 1 Do i=1, 5 READ(*, *) array 1(i) END DO • Initializing arrays in declaration (OK for small arrays) INTEGER, DIMENSION(5) : : array 1 =(/1, 2, 3, 4, 5/) Number of values must be equal to the array size • Declaring arrays using implied loops INTEGER, DIMENSION(100) : : array 1 = ( / ( i , i=1, 100) / ) General form of implied loop (arg 1, arg 2, …, index = istart, iend, incr)

Example-2 PROGRAM square_roots IMPLICIT NONE INTEGER : : i INTEGER, DIMENSION(10) : : value = (/ (i, i = 1, 10) /) INTEGER, DIMENSION(10) : : s_root DO i=1, 10 s_root(i) = SQRT(value(i)) END DO DO i=1, 10 WRITE(*, *) values(i), ' END DO END PROGRAM ', s_root(i)

More Implied loops • INTEGER, DIMENSION(25) : : array = ( ((0, i=1, 4), 5*j, j=1, 5) ) (arg 1, arg 2, …, index = istart, iend, incr) • array = 0, 0, 5, 0, 0, 10, 0, 0, 15, 0, 0, 20, 0, 0, 25 • INTEGER, DIMENSION(25) : : array = ( ((j, 2*j, 3*j, j=1, 3) ) • array = 1, 2, 3, 2, 4, 6, 3, 6, 9

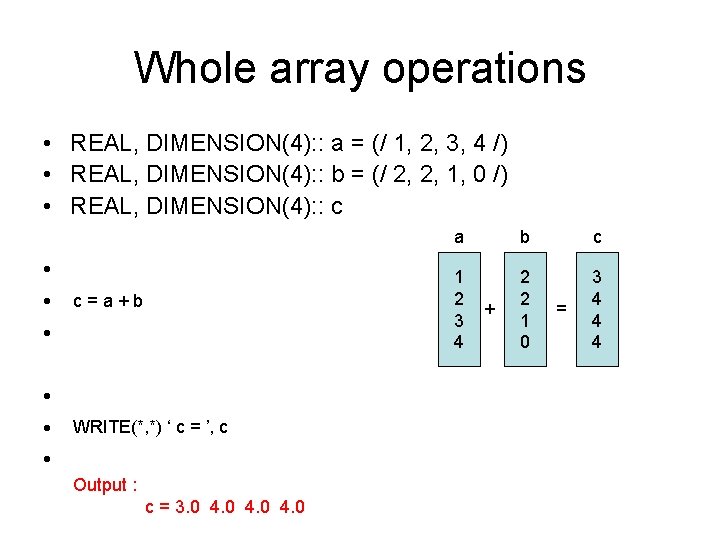
Whole array operations • REAL, DIMENSION(4): : a = (/ 1, 2, 3, 4 /) • REAL, DIMENSION(4): : b = (/ 2, 2, 1, 0 /) • REAL, DIMENSION(4): : c • DO i = 1, 4 c = a=+ a(i) b • c(i) + b(i) • END DO • DO i = 1, 4 WRITE(*, *) ‘ c =c(i) ’, c • WRITE(*, *) • END DO Output : c = 3. 0 4. 0 a b c 1 2 3 4 2 2 1 0 3 4 4 4 + =

Out of bound subscripts • REAL, DIMENSION(5) : : array • array should have 5 values numbered 1 to 5 • Any other subscript out of these bounds (1, 5) will result in an out of bounds error either detected by compiler (if compiler bounds check is turned on) or at run time.

Example-3 PROGRAM summation IMPLICIT NONE INTEGER : : i REAL, DIMENSION(6) : : x=(/ 1. , 2. , 3. , 4. , 5. , 6. /) REAL, DIMENSION(6) : : a=(/. 1, . 2, . 2/) REAL : : total=0 DO i=1, 6 total = total + (2*x(i)+a(i)) END DO WRITE (*, *) 'Total = ', total END PROGRAM _______________________ What does this program do?

Changing the Subscript Range of an Array • REAL, DIMENSION(5): : arr Elements arr(1), arr(2), arr(3), arr(4), arr(5) Change range • REAL, DIMESION(-2: 2) Elements arr(-2), arr(-1), arr(0), arr(1), arr(2) • What is he sixze of the following array? REAL, DIMENSION(-1: 19) Size = upper – lower +1 = 19 - -1 +1 = 21

Out of bounds INTEGER, DIMESION(5): : arr Do i=1, 5 WRITE(*, *) arr(i) END DO INTEGER, DIMESION(-2: 2): : arr Do i=-2, 2 WRITE(*, *) arr(i) END DO

Array subset arr(subscript 1 : subscript 2: increment) INTEGER, DIMENSION(10): : a=(/1. , -2. , 3. , -4. , 5. , -6. , 7. , -8. , 9. , -10. /) • Find the following subsets: – – – – arr(: ) arr(3: 7: 2) arr(3: 7: 7) arr(: 6) arr(5: ) arr(: : 2)

Example INTEGER, DIMENSION(3): : x=(/2, 5, 8/) INTEGER, DIMENSION(5): : y=(/1, 3, 2, 4, 7/) INTEGER, DIMENSION(2): : z z = x(1: 2) + y(3: 4) WRITE(*, *) z z = 4, 9

Vector Subscript • The subset in previous slides used subscript triplets array(a: b: c) • Vector subscript is using a vector or array as index values of another array. INTEGER, DIMENSION(5): : vec=(/1, 6, 4, 1, 9/) REAL, DIMENSION(10): : a=(/1, -2, 3, -4, 5, -6, 7, -8, 9, -10/) WRITE(*, *) a(vec) Output: a(1), a(6), a(4), a(1), a(9) 1, -6, -4, 1, 9

Subset Assignment INTEGER, DIMENSION(5): : vec=(/1, 6, 4, 1, 9/) REAL, DIMENSION(10): : a=(/1, -2, 3, -4, 5, -6, 7, -8, 9, -10/) REAL, DIMENSION(10): : b=(/1, -2, 3, -4, 5, -6, 7, -8, 9, -10/) a(2: 8: 2)=(/1, -1, 1, -1/) b(vec)=(/1, -1, 1/) WRITE(*, *) ‘a = ’, a WRITE (*, *) ‘b = ’, b Output : a = 1, 1, 3, -1, 5, 1, 7, -1, 9, -10 b = -1, -2, 3, 1, 5, -1, 7, -8, 1, -10

Simple Output Format INTEGER : : a=10 REAL : : b=5. 1 WRITE(*, *) a, b Output: 10 5. 10000000 WRITE(*, 100) a, b 100 FORMAT(I 2, F 10. 8) Output: 105. 10000000 WRITE(*, 100) a, b 100 FORMAT(I 2, 1 X, F 10. 8) Output: 10 5. 10000000 WRITE(*, 100) a, b 100 FORMAT(I 2, 3 X, F 3. 1) Output: 10 5. 1 WRITE(*, 100) a, b 100 FORMAT(' a= ', I 2, 3 X, 'b= ', F 3. 1) Output: a= 10 b= 5. 1

Input/output of array elements REAL, DIMENSION(5) : : a= (/0. 5, -1, 0. 1, 2. , 10. 4/) WRITE(*, *) (a(i), i=1, 5) Output: 0. 50000 -1. 0000 0. 100000001 2. 0000 10. 40000000 Do i=1, 5 WRITE(*, *) a(i) END DO Output: 0. 50000 -1. 0000 0. 10000 2. 0000 10. 40000000 WRITE(*, 100) a(1), a(2), a(3), a(4), a(5) 100 FORMAT (1 X, 'a =', 5 F 7. 2) Output: a = 0. 50 -1. 00 0. 10 2. 00 10. 40 WRITE(*, 100) (a(i), i=1, 5) 100 FORMAT (F 10. 2) Output: 0. 50 -1. 00 0. 10 2. 00 10. 40 WRITE(*, 100) (a(i), i=1, 5) 100 FORMAT (5 F 10. 2) Output: 0. 50 -1. 00 0. 10 2. 00 10. 40

Input/Output with implied loops WRITE(unit, format)(arg 1, ar 2, . . , index=istart, iend, incr) READ(unit, format)(arg 1, ar 2, . . , index=istart, iend, incr) WRITE(*, *) (i, 2*I, 3*I, i=1, 3) Output: 1 2 3 2 4 6 3 6 9 WRITE(*, 100) (a(i), i=1, 5) 100 (1 X, ‘a= ’, 5 F 7. 2) WRITE(*, 200) ((i, j, j=1, 3), i=1, 2) 200 FORMAT(1 X, I 5, 1 X, I 5) Output: 1 1 1 2 1 3 2 1 2 2 2 3

Two-Dimensional Array • Rank-2 array require 2 subscripts as an address to retrieve one value. array(a, b) a is the index in the first dimension b is the index in the second dimension • Declaring 2 -D array REAL, DIMENSION(3, 6) : : arr 1 REAL, DIMENSION(-1: 9, 0: 19) : : arr 2 INTEGER, DIMENSION(10, 0: 19) : : arr 3

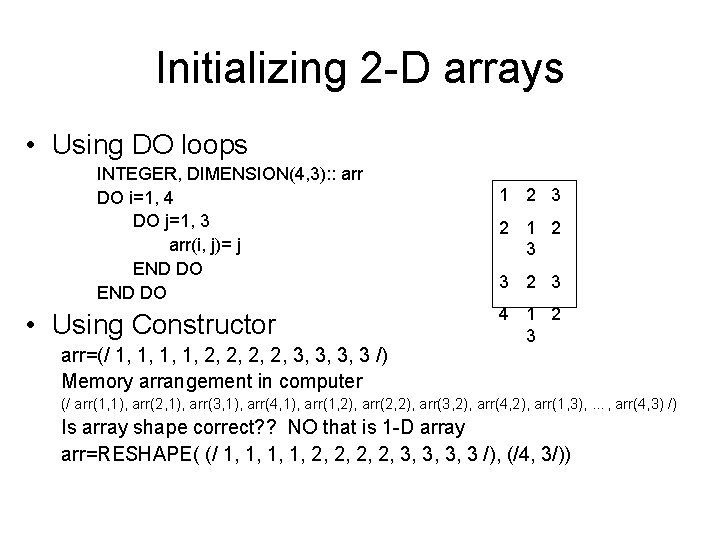
Initializing 2 -D arrays • Using DO loops INTEGER, DIMENSION(4, 3): : arr DO i=1, 4 DO j=1, 3 arr(i, j)= j END DO • Using Constructor arr=(/ 1, 1, 2, 2, 3, 3, 3, 3 /) Memory arrangement in computer 1 2 3 2 1 2 3 3 2 3 4 1 2 3 (/ arr(1, 1), arr(2, 1), arr(3, 1), arr(4, 1), arr(1, 2), arr(2, 2), arr(3, 2), arr(4, 2), arr(1, 3), …, arr(4, 3) /) Is array shape correct? ? NO that is 1 -D array arr=RESHAPE( (/ 1, 1, 2, 2, 3, 3, 3, 3 /), (/4, 3/))

Initializing 2 -D arrays • Initializing in Declaration INTEGER, DIMENSION(4, 3): : arr=RESHAPE ( (/ 1, 1, 2, 2, 3, 3, 3, 3 /), (/4, 3/)) • Initializing using READ(*, *) arr READ(*, *) ((arr(i, j), j=1, 3), i=1, 4)

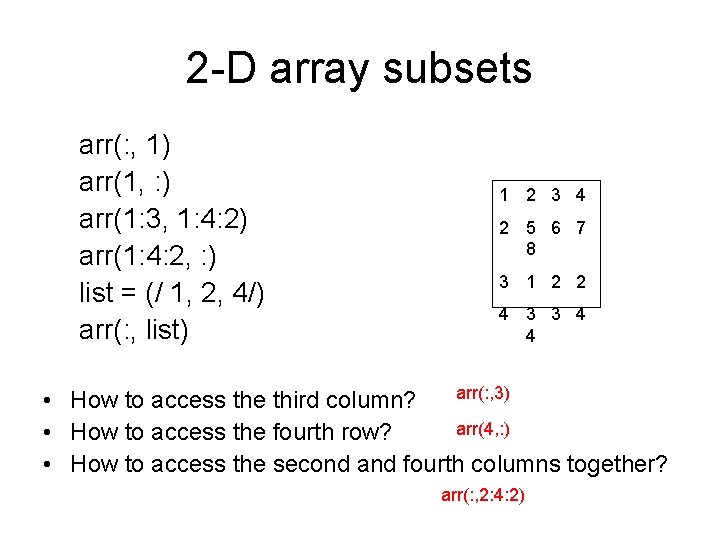
2 -D array subsets arr(: , 1) arr(1, : ) arr(1: 3, 1: 4: 2) arr(1: 4: 2, : ) list = (/ 1, 2, 4/) arr(: , list) 1 2 3 4 2 5 6 7 8 3 1 2 2 4 3 3 4 4 arr(: , 3) • How to access the third column? arr(4, : ) • How to access the fourth row? • How to access the second and fourth columns together? arr(: , 2: 4: 2)

2 -D array output WRITE (*, *) arr 111122223333 DO j=1, 3 DO i=1, 4 WRITE (*, *) arr(i, j) END DO DO i=1, 4 DO j=1, 3 WRITE (*, *) arr(i, j) END DO WRITE (*, *) ((arr(i, j), i=1, 4), j=1, 3) 111122223333 DO i=1, 4 WRITE (*, *) (arr(i, j), j=1, 3) END DO 1 1 2 2 3 2 1 2 2 2 3 3 1 3 2 3 3 3 1 2 3 2 1 2 3 3 2 3 1 1 2 3 4 1 2 3

2 -D array example-1 1. Write a program that initializes a 3 X 4 matrix as shown below. The program should make search for minimum and maximum values in the 2 -D array. 1. 5 2. -3. 1 4. 0 5. 9. 6 7. 7 -8. 1. 1 0. 1 2. 1 -2. 2. Repeat the above program but let the user now enter the values of the matrix via the keyboard.

2 -D array example-2 1. Write a program that initializes a 3 X 4 matrix as shown below. The program should count how many positive numbers, negative numbers and zeros in the matrix. 1. 5 2. -3. 1 4. 0 5. 9. 6 7. 7 -8. 1. 1 0. 1 2. 1 -2. 2. Repeat the above program but let the user now enter the values of the matrix via the keyboard.

Matrix Operations • Write a program that accepts two matrices from the user and store them in two 2 -D arrays. Then, the program prompt the user to select the operation he is seeking by entering 1 for matrix addition, 2 for matrix subtraction, and 3 for matrix multiplication. Addition and subtraction are done element by element for two matrices that are having the same size. The multiplication is done for two matrixes where the number of columns in the first matrix is equal to the number of rows in the second one. C=A+B (MXN) = (MXN) + (MXN) C=A-B (MXN) = (MXN) - (MXN) C=AXB (MXN) = (MXL) + (LXN) Multiplication can be done as follows