Chapter 6 Integer Goal and Nonlinear Programming Models

Chapter 6 Integer, Goal, and Nonlinear Programming Models © 2007 Pearson Education

Variations of Basic Linear Programming • Integer Programming • Goal Programming • Nonlinear Programming

Integer Programming (IP) Where some or all decision variables are required to be whole numbers. • General Integer Variables (0, 1, 2, 3, etc. ) Values that count how many • Binary Integer Variables (0 or 1) Usually represent a Yes/No decision

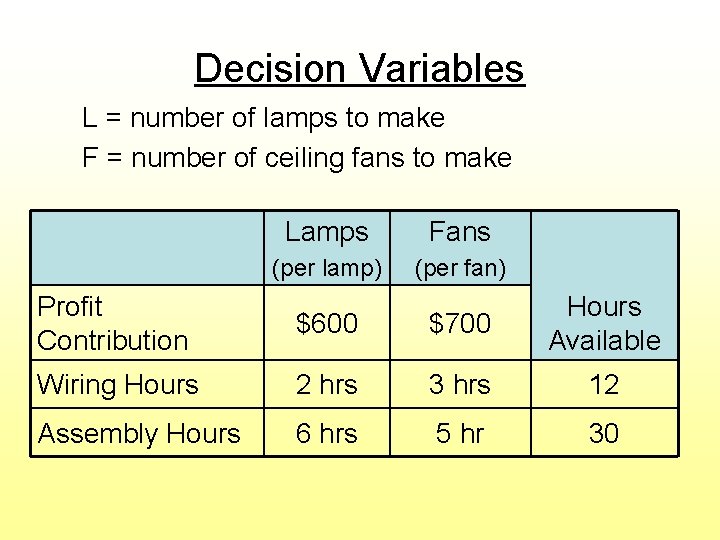
General Integer Example: Harrison Electric Co. Produce 2 products (lamps and ceiling fans) using 2 limited resources Decision: How many of each product to make? (must be integers) Objective: Maximize profit

Decision Variables L = number of lamps to make F = number of ceiling fans to make Lamps Fans (per lamp) (per fan) Profit Contribution $600 $700 Hours Available Wiring Hours 2 hrs 3 hrs 12 Assembly Hours 6 hrs 5 hr 30

LP Model Summary Max 600 L + 700 F ($ of profit) Subject to the constraints: 2 L + 3 F < 12 (wiring hours) 6 L + 5 F < 30 (assembly hours) L, F > 0

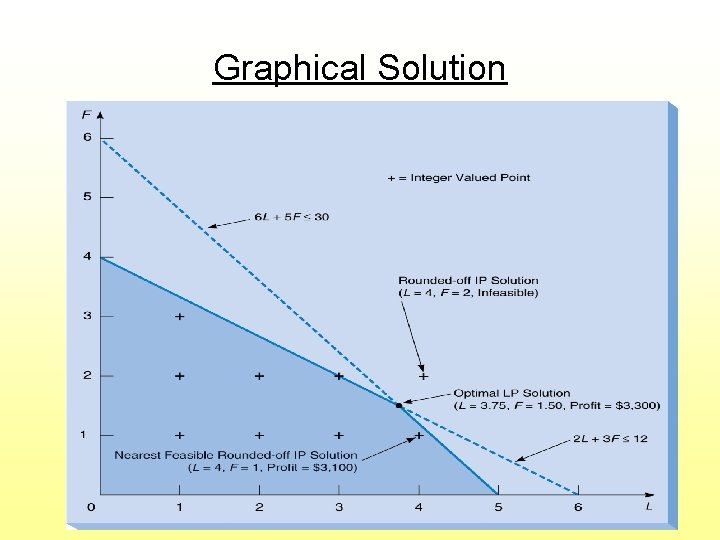
Graphical Solution

Properties of Integer Solutions • Rounding off the LP solution might not yield the optimal IP solution • The IP objective function value is usually worse than the LP value • IP solutions are usually not at corner points

Using Solver for IP • IP models are formulated in Excel in the same way as LP models • The additional integer restriction is entered like an additional constraint - Means general integer variables bin - Means binary variables Go to file 6 -1. xls

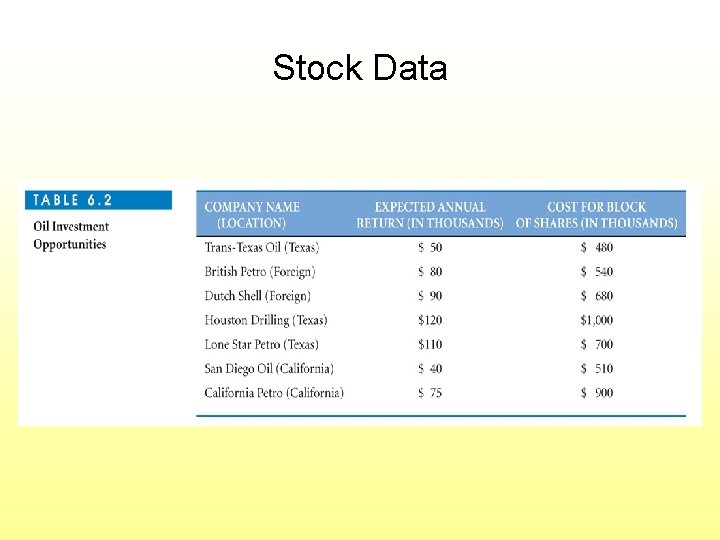
Binary Integer Example: Portfolio Selection Choosing stocks to include in portfolio Decision: Which of 7 stocks to include? Objective: Maximize expected annual return (in $1000’s)

Stock Data

Decision Variables Use the first letter of each stock’s name Example for Trans-Texas Oil: T = 1 if Trans-Texas Oil is included T = 0 if not included

Restrictions • • • Invest up to $3 million Include at least 2 Texas companies Include no more than 1 foreign company Include exactly 1 California company If British Petro is included, then Trans-Texas Oil must also be included

Objective Function (in $1000’s return) Max 50 T + 80 B + 90 D + 120 H + 110 L + 40 S + 75 C Subject to the constraints: Invest up to $3 Million 480 T + 540 B + 680 D + 1000 H + 700 L + 510 S + 900 C < 3000

Include At Least 2 Texas Companies T+H+L > 2 Include No More Than 1 Foreign Company B+D < 1 Include Exactly 1 California Company S+C = 1

If British Petro is included (B=1), then Trans-Texas Oil must also be included (T=1) Combinations of B and T B=0 T=1 ok ok B=1 not ok ok B<T allows the 3 acceptable combinations and prevents the unacceptable one Go to file 6 -3. xls

Mixed Integer Models: Fixed Charge Problem • Involves both fixed and variable costs • Use a binary variable to determine if a fixed cost is incurred or not • Either linear or general integer variables deal with variable cost

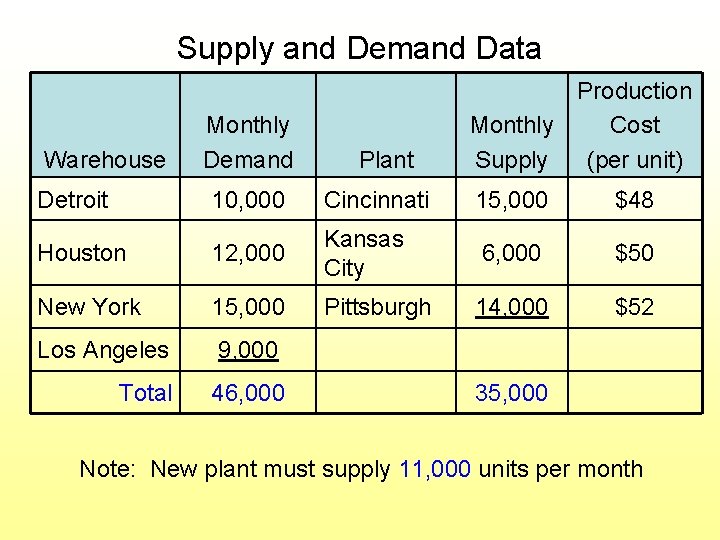
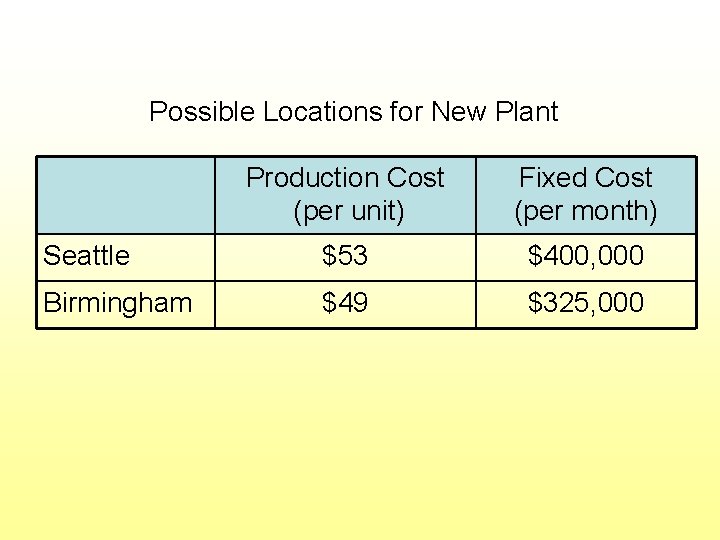
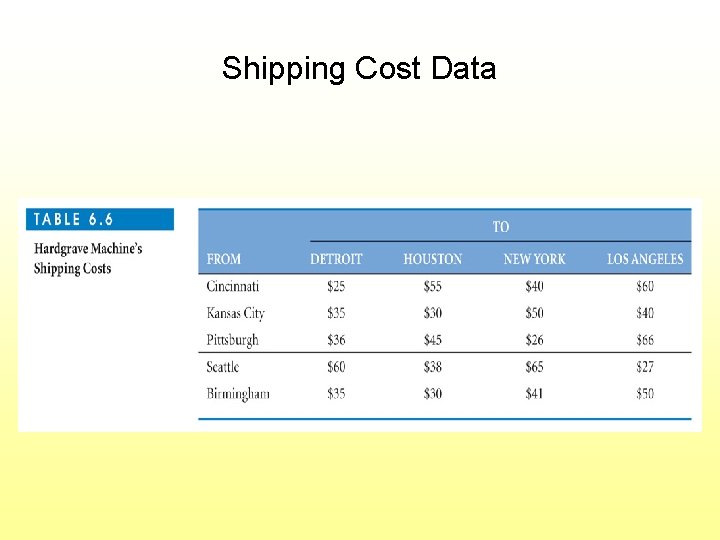
Fixed Charge Example: Hardgrave Machine Co. Has 3 plants and 4 warehouses and is considering 2 locations for a 4 th plant Decisions: • Which location to choose for 4 th plant? • How much to ship from each plant to each warehouse? Objective: Minimize total production and shipping cost

Supply and Demand Data Warehouse Detroit Monthly Demand Plant Production Cost Monthly Supply (per unit) 10, 000 Cincinnati 15, 000 $48 Houston 12, 000 Kansas City 6, 000 $50 New York 15, 000 Pittsburgh 14, 000 $52 Los Angeles 9, 000 Total 46, 000 35, 000 Note: New plant must supply 11, 000 units per month

Possible Locations for New Plant Production Cost (per unit) Fixed Cost (per month) Seattle $53 $400, 000 Birmingham $49 $325, 000

Shipping Cost Data

Decision Variables Binary Variables Ys = 1 if Seattle is chosen = 0 if not YB = 1 if Birmingham is chosen = 0 if not Regular Variables Xij = number of units shipped from plant i to warehouse j

Objective Function (in $ of cost) Min 73 XCD + 103 XCH + 88 XCN + 108 XCL + 85 XKD + 80 XKH + 100 XKN + 90 XKL + 88 XPD + 97 XPH + 78 XPN + 118 XPL + 113 XSD + 91 XSH + 118 XSN + 80 XSL + 84 XBD + 79 XBH + 90 XBN + 99 XBL + 400, 000 YS + 325, 000 YB Subject to the constraints: (see next slide)

Supply Constraints -(XCD + XCH + XCN + XCL) = -15, 000 (Cincinnati) -(XKD + XKH + XKN + XKL) = - 6, 000 (Kansas City) -(XPD + XPH + XPN + XPL) = -15, 000 (Pittsburgh) Possible Locations for New Plant -(XSD + XSH + XSN + XSL) = -11, 000 YS (Seattle) -(XBD + XBH + XBN + XBL) = -11, 000 YB (B’ham)

Demand Constraints XCD + XKD + XPD +XSD + XBD = 10, 000 XCH + XKH + XPH +XSH + XBH = 12, 000 XCN + XKN + XPN +XSN + XBN = 15, 000 XCL + XKL + XPL +XSL + XBL = 9, 000 (Detroit) (Houston) (New York) Choose 1 New Plant Location YS + YB =1 Go to File 6 -5. xls (L. A. )

Goal Programming Models • Permit multiple objectives • Try to “satisfy” goals rather than optimize • Objective is to minimize underachievement of goals

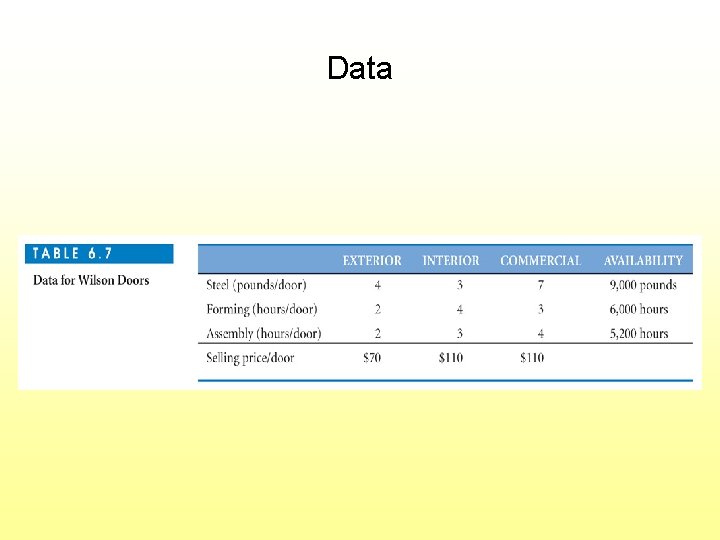
Goal Programming Example: Wilson Doors Co. Makes 3 types of doors from 3 limited resources Decision: How many of each of 3 types of doors to make? Objective: Minimize total underachievement of goals

Data

Goals 1. Total sales at least $180, 000 2. Exterior door sales at least $70, 000 3. Interior door sales at lest $60, 000 4. Commercial door sales at least $35, 000

Regular Decision Variables E = number of exterior doors made I = number of interior doors made C = number of commercial doors made Deviation Variables di+ = amount by which goal i is overachieved di- = amount by which goal i is underachieved

Goal Constraints Goal 1: Total sales at least $180, 000 70 E + 110 I + 110 C + d. T- - d. T+ = 180, 000 Goal 2: Exterior door sales at least $70, 000 70 E + d. E- - d. E+ = 70, 000 Note: Each highlighted deviation variable measures goal underachievement

Goal 3: Interior door sales at least $60, 000 110 I + d. I- - d. I+ = 60, 000 Goal 4: Commercial door sales at least $35, 000 110 C + d. C- - d. C+ = 35, 000

Objective Function Minimize total goal underachievement Min d. T- + d. E- + d. I- + d. CSubject to the constraints: • The 4 goal constraints • The “regular” constraints (3 limited resources) • nonnegativity

Weighted Goals • When goals have different priorities, weights can be used • Suppose that Goal 1 is 5 times more important than each of the others Objective Function Min 5 d. T- + d. E- + d. I- + d. C-

Properties of Weighted Goals • Solution may differ depending on the weights used • Appropriate only if goals are measured in the same units

Ranked Goals • Lower ranked goals are considered only if all higher ranked goals are achieved • Suppose they added a 5 th goal Goal 5: Steel usage as close to 9000 lb as possible 4 E + 3 I + 7 C + d. S= 9000 (lbs steel) (no d. S+ is needed because we cannot exceed 9000 pounds)

• • • Rank R 1: Goal 1 Rank R 2: Goal 5 Rank R 3: Goals 2, 3, and 4 A series of LP models must be solved 1) Solve for the R 1 goal while ignoring the other goals Objective Function: Min d. TGo to file 6 -7. xls

2) If the R 1 goal can be achieved (d. T- = 0), then this is added as a constraint and we attempt to satisfy the R 2 goal (Goal 5) Objective Function: Min d. S 3) If the R 2 goal can be achieved (d. S- = 0), then this is added as a constraint and we solve for the R 3 goals (Goals 2, 3, and 4) Objective Function: Min d. E- + d. I- + d. C-

Nonlinear Programming Models • Linear models (LP, IP, and GP) have linear objective function and constraints • If a model has one or more nonlinear equations (objective or constraint) then the model is nonlinear • Example nonlinear terms: X 2, 1/X, XY

Characteristics of Nonlinear Programming (NLP) Models • Difficult to solve • Optimal solutions are not necessarily at corner points • There are both local and global optimal solutions • Solution may depend on starting point • Starting point is usually arbitrary

Nonlinear Programming Example: Pickens Memorial Hospital Patient demand exceeds hospital’s capacity Decision: How many of each of 3 types of patients to admit per week? Objective: Maximize profit

Decision Variables M = number of Medical patients to admit S = number of Surgical patients to admit P = number of Pediatric patients to admit Profit Function Profit per patient increases as the number of patients increases (i. e. nonlinear profit function)

Constraints • Hospital capacity: 200 total patients • X-ray capacity: 560 x-rays per week • Marketing budget: $1000 per week • Lab capacity: 140 hours per week

Objective Function (in $ of profit) Max 45 M + 2 M 2 + 70 S + 3 S 2 + 2 MS + 60 P + 3 P 2 Subject to the constraints: M+S+P < 200 (patient cap. ) M + 3 S + P < 560 (x-ray cap. ) 3 M + 5 S + 3. 5 P < 1000 (marketing $) (0. 2+0. 001 M)x(3 M+3 S+3 P) < 140 (lab hrs) M, S, P > 0

Using Solver for NLP Models • Solver uses the Generalized Reduced Gradient (GRG) method • GRG uses the path of steepest ascent (or descent) • Moves from one feasible solution to another until the objective function value stops improving (converges) Go to file 6 -8. xls