Chapter 6 Inferences Based on a Single Sample

Chapter 6 Inferences Based on a Single Sample: Estimation with Confidence Intervals

Large-Sample Confidence Interval for a Population Mean How to estimate the population mean and assess the estimate’s reliability? is an estimate of , and we use CLT to assess how accurate that estimate is According to CLT, 95% of all from sample size n lie within of the mean We can use this to assess accuracy of estimate of as an
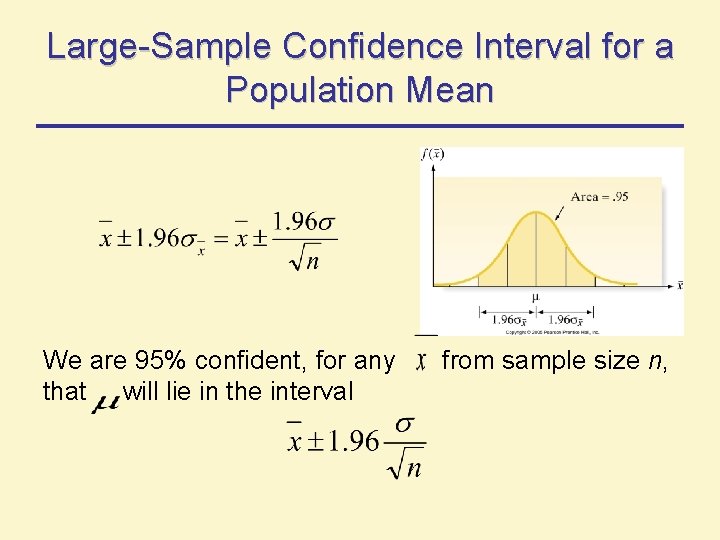
Large-Sample Confidence Interval for a Population Mean We are 95% confident, for any that will lie in the interval from sample size n,

Large-Sample Confidence Interval for a Population Mean We usually don’t know a good estimator of , but with a large sample s is We can calculate confidence intervals for different confidence coefficients Confidence coefficient – probability that a randomly selected confidence interval encloses the population parameter Confidence level – Confidence coefficient expressed as a percentage
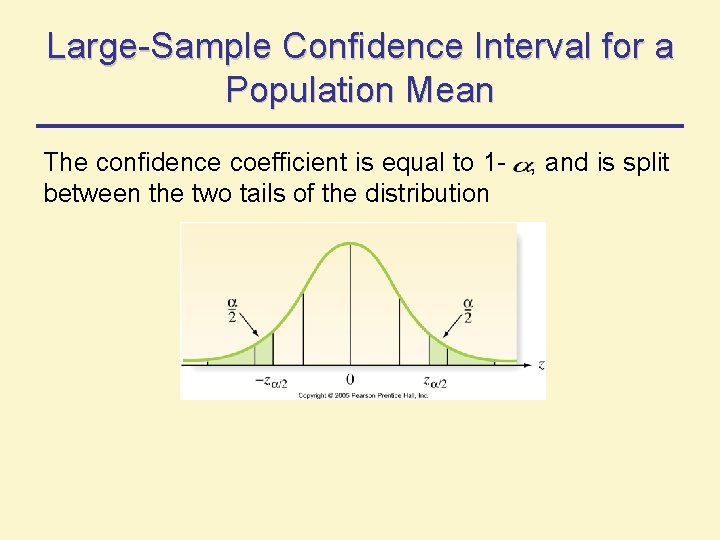
Large-Sample Confidence Interval for a Population Mean The confidence coefficient is equal to 1 - , and is split between the two tails of the distribution

Large-Sample Confidence Interval for a Population Mean The Confidence Interval is expressed more generally as For samples of size > 30, the confidence interval is expressed as
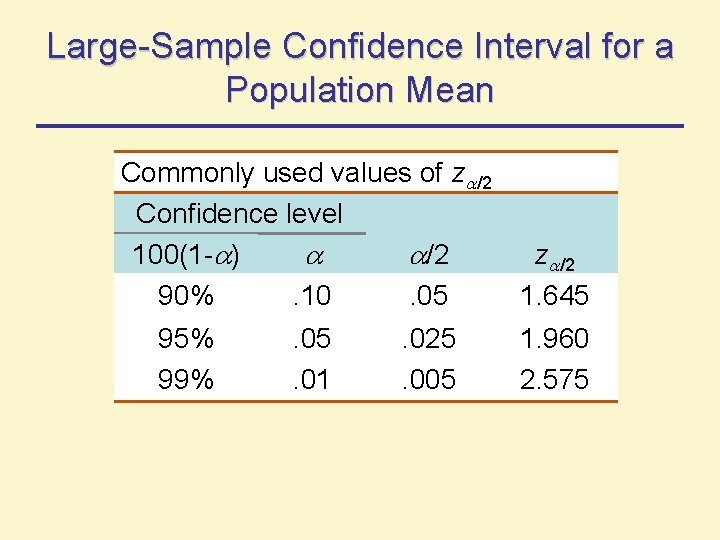
Large-Sample Confidence Interval for a Population Mean Commonly used values of z /2 Confidence level 100(1 - ) /2 z /2 90%. 10. 05 1. 645 95% 99% . 05. 01 . 025. 005 1. 960 2. 575

Small-Sample Confidence Interval for a Population Mean 2 problems presented by sample sizes of <30: • CLT no longer applies • Population standard deviation is unknown, and s may provide a poor estimation of when n is small If the sampled population is approximately normal, then the sampling distribution of can be assumed to be approximately normal Instead of using we use the t-statistic
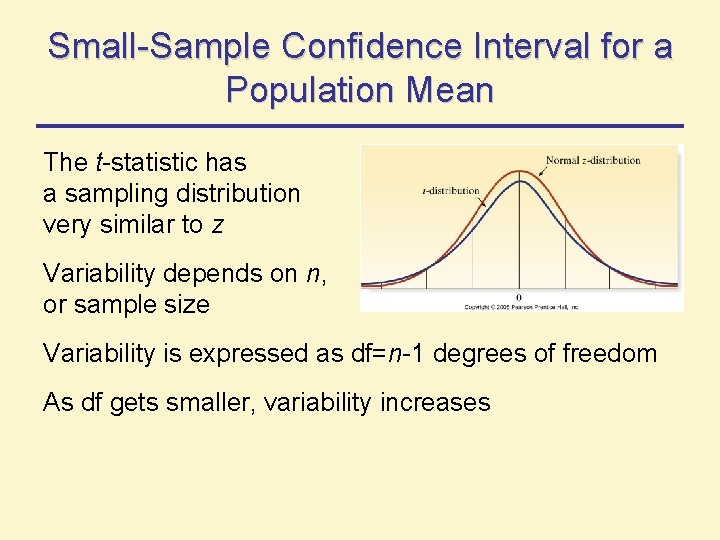
Small-Sample Confidence Interval for a Population Mean The t-statistic has a sampling distribution very similar to z Variability depends on n, or sample size Variability is expressed as df=n-1 degrees of freedom As df gets smaller, variability increases
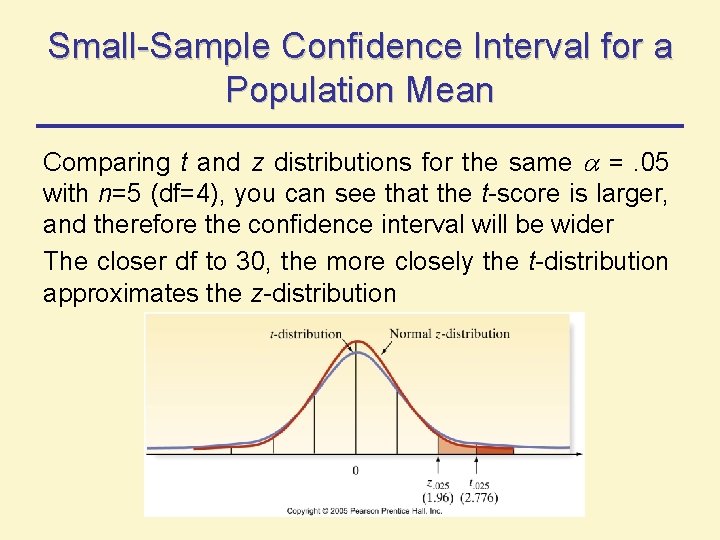
Small-Sample Confidence Interval for a Population Mean Comparing t and z distributions for the same =. 05 with n=5 (df=4), you can see that the t-score is larger, and therefore the confidence interval will be wider The closer df to 30, the more closely the t-distribution approximates the z-distribution

Small-Sample Confidence Interval for a Population Mean When creating a confidence interval around for a small sample we use basing t /2 on df=n-1 degrees of freedom

Large-Sample Confidence Interval for a Population Proportion Sample statistic of interest is The mean of the sampling distribution of unbiased estimator of p is p, is an The standard deviation of the sampling distribution is , where q = 1 -p For large samples, the sampling distribution of approximately normal is

Large-Sample Confidence Interval for a Population Proportion Sample size n is large if fall between 0 and 1 Confidence interval is calculated as where and

Large-Sample Confidence Interval for a Population Proportion When p is near 0 or 1, the confidence intervals calculated using the formulas presented are misleading An adjustment can be used that works for any p, even with very small sample sizes:

Determining the Sample Size When we want to estimate to within some number units with a (1 - ) level of confidence, we can calculate the sample size needed We use the Sampling Error (SE), which is half the width of the confidence interval To estimate with SE and 100(1 - )% confidence, where is estimated by s or R/4.

Determining the Sample Size Assume a sample with = 0. 01 and a range R =. 4 What size sample do we need to achieve a desired SE of. 025 ?

Determining the Sample Size Sample size can also be estimated for population proportion p: Estimates with a value of p being equal or close to 0. 5 are the most conservative

Finite Population Correction for Simple Random Sampling Used when the sample size n is large relative to the size of the population N, n/N >. 05 Standard error calculation for with correction: Standard error calculation for p with correction:
- Slides: 18