Chapter 6 Gravitation Newtons Law of Universal Gravitation

Chapter 6 Gravitation

Newtons Law of Universal Gravitation For any two masses in the universe the force of attraction is: G = a universal constant = m 1 +F -F r m 2

Two people pass in a hall. Find the small gravitational attractive force between them. Assume each person is a spherical. 1 millionth of an ounce As you can see it is negligible compared to our everyday contact forces

Newton: G does not change with matter. Newton built pendula of different materials, and measured G at a fixed location, finding it to remain constant. Therefore he concluded that G is independent of the kind of matter. All that counts is mass.

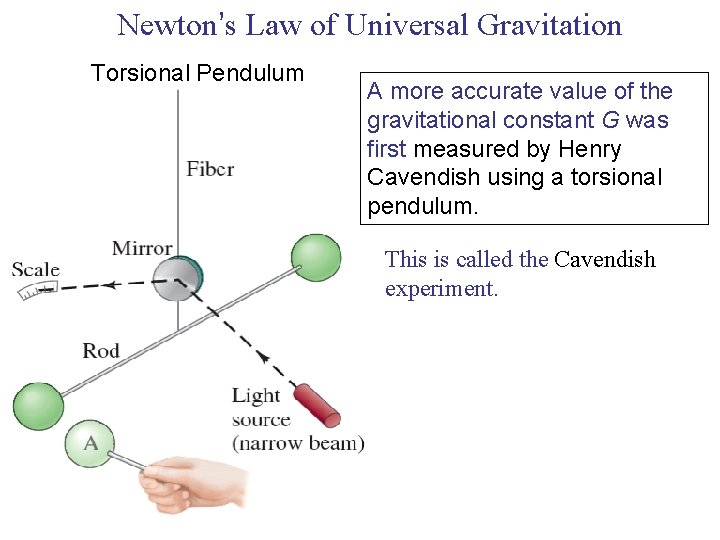
Newton’s Law of Universal Gravitation Torsional Pendulum A more accurate value of the gravitational constant G was first measured by Henry Cavendish using a torsional pendulum. This is called the Cavendish experiment.

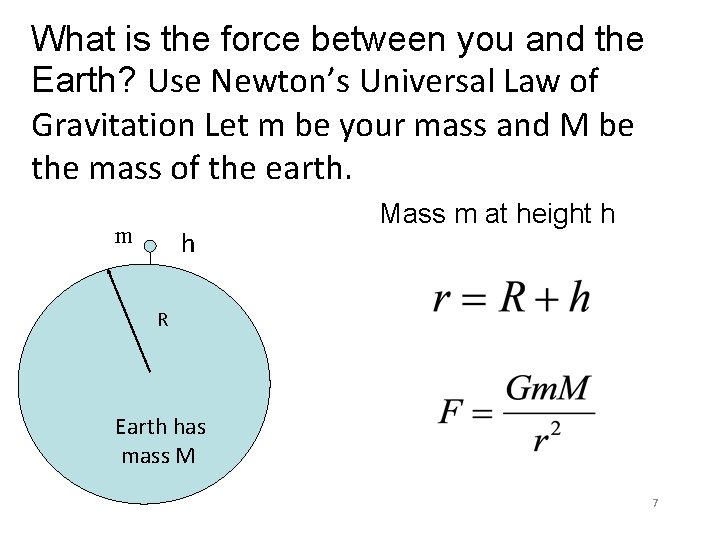
The force of gravity is small unless you have a massive object. For example: • What is the force between you and the Earth? • How is related to your weight mg? • Where does the value of g come from? 6

What is the force between you and the Earth? Use Newton’s Universal Law of Gravitation Let m be your mass and M be the mass of the earth. m h Mass m at height h R Earth has mass M 7

Mass m at height h h R Earth has mass M 8

How is related to your weight mg? Mass m at height h h R Earth has mass M Used mean radius of the Earth 9

Gravity Near the Earth’s Surface; Geophysical Applications The acceleration due to gravity varies over the Earth’s surface due to altitude, local geology, and the shape of the Earth, which is not quite spherical.

Three reasons why you weight may vary At the equator the earths effective g is 9. 7805 m/s 2. The acceleration at the equator due to the earths rotation is 0. 0339 m/s 2 and reduces the earths effective g. This means that the true gravitational acceleration is 9. 7805+0. 0339 = 9. 8144 m/s 2 At the poles the Gravitational acceleration is 9. 8322 m/s 2. The difference between the poles and the equator is that objects on the Equator are still about 21 km away from the center of the earth. Your weight is still slightly smaller at both locations due to 11 the small buoyancy effect of the atmosphere.

Amount you weigh less at the equator At the equator, a 70 kg person would weigh less by:

Some properties of Newton’s Gravitational Inverse Square Force Law m 1 r m 2 1. The force between two solid spherical masses or two shells of different radii is the same as the difference between two point masses separated by their centers R 2 R 1 r r m 1 m 2

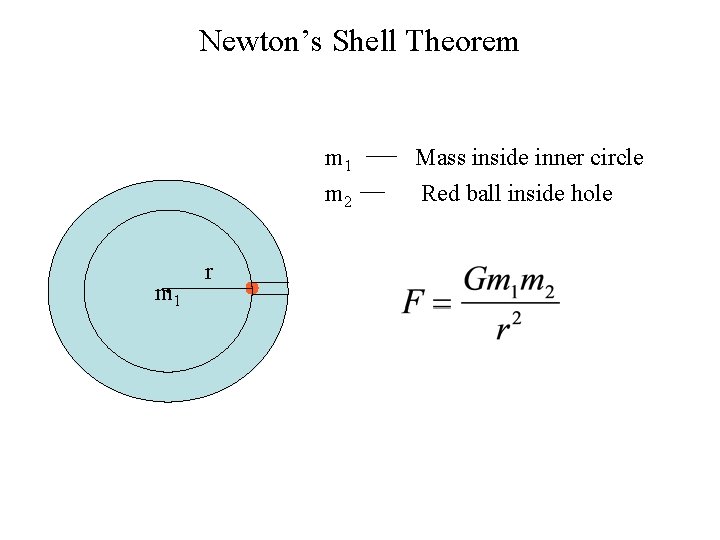
Newton’s Shell Theorem A uniform shell of matter exerts no net gravitational force on a particle located inside it F=0 A uniform spherical shell of matter attracts a particle that is outside the shell as if all the shell’s mass were concentrated at its center. r m 2 m 1

Newton’s Shell Theorem m 1 m 2 m 1 r Mass inside inner circle Red ball inside hole

How is mass defined? 1. You can measure the force acting on it and measure the acceleration and take the ratio. mi = F/a This mass is called the inertial mass. 2. You can weigh it and divide by g. This is called the gravitational mass. For all practical purposes they are equivalent,

Principle of Superposition and the vector nature of the gravitational force The force F on mass m 1 is the vector sum of the forces on it due to m 2 and m 3

Principle of Superposition φ If m 2 =m 3, then φ=76. 0 deg

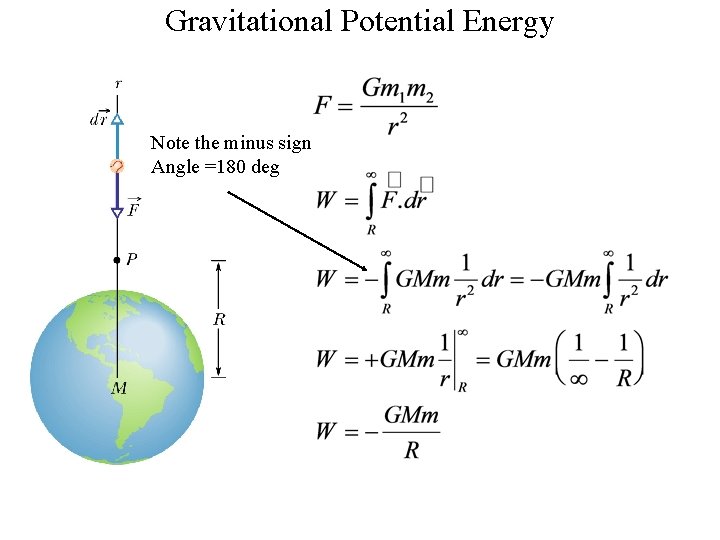
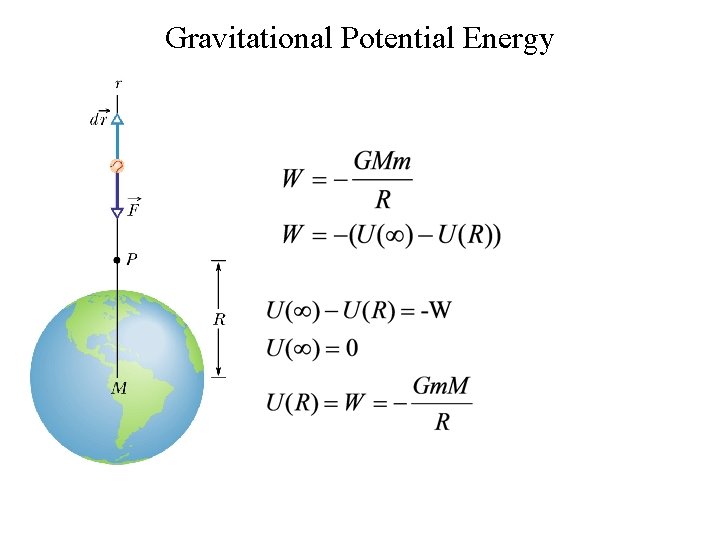
We want to find the potential energy for the gravitational force acting on a particle far outside the Earth Baseball Let’s find the work done on a mass moving in a gravitational field from r to infinity

Gravitational Potential Energy Note the minus sign Angle =180 deg

Gravitational Potential Energy

Difference in potential energy between two points only depends on end points. The difference in potential energy in a mass m moving from A to G is r. G r. A M

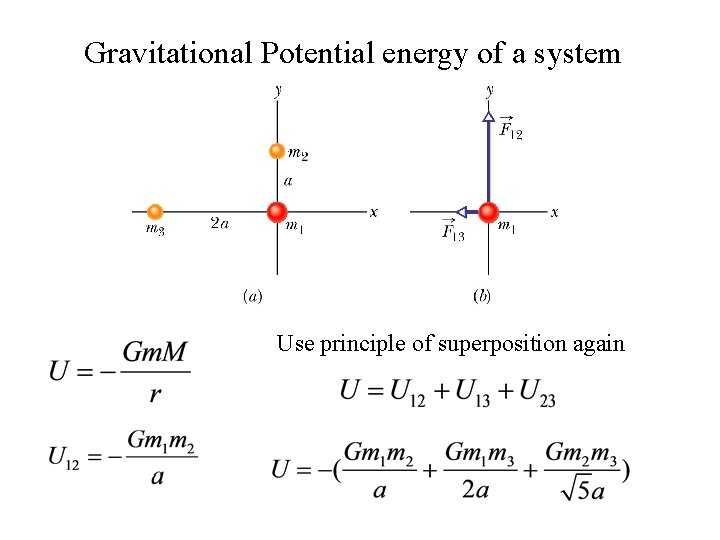
Gravitational Potential energy of a system Use principle of superposition again

How is our old definition U=mgh related to our new definition of potential energy h R So if we measure U relative to the surface we get the same result

Some consequences of a 1/r 2 potential Escape Speed There is a certain minimum initial speed that when you fire a projectile upward it will never return. It has total energy At the surface of the Earth it has When it just reaches infinity it has 0 kinetic energy and 0 potential energy so its total energy is zero. Since energy is conserved it must also have 0 at the Earth’s surface. Solve for v Some escape speeds Moon 2. 38 km/s = 5, 331 mi/hr Earth 11. 2 km/s = 25, 088 mi/hr Sun 618 km/s = 1, 384, 320 mi/hr

• A projectile is fired vertically from the surface of the earth with a speed of 10 km/s. Neglecting air drag, how far will it go? r h R

Energies for orbiting satellites or planets (True in general for inverse square law) For a earth in orbit around the sun or a satellite in a circular orbit around the earth The total energy is E = K + U Note that the total energy is the negative of the kinetic energy. A negative total energy means the system is bound. For an elliptical orbit E = - GMm/2 a where a is the semi major axis

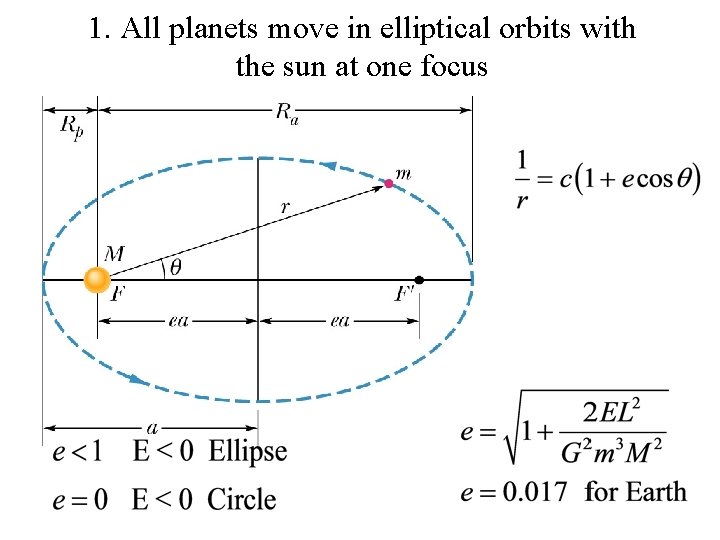
Kepler’s 3 Laws 1. Law of Orbits: All planets move in elliptical orbits with the sun at one focus 2. The Law of Areas: A line that connects a planet to the sun sweeps out equal areas in the plane of the planets orbit in equal time intervals. d. A/dt is constant 3. The Law of Periods: The square of the period of any planet is proportional to the cube of the semimajor axis of its orbit

1. All planets move in elliptical orbits with the sun at one focus

1. All planets move in elliptical orbits with the sun at one focus

1. All planets move in elliptical orbits with the sun at one focus E is the total energy and is equal to the kinetic energy plus potential energy

Comets and asteroids can have other conic sections or paths

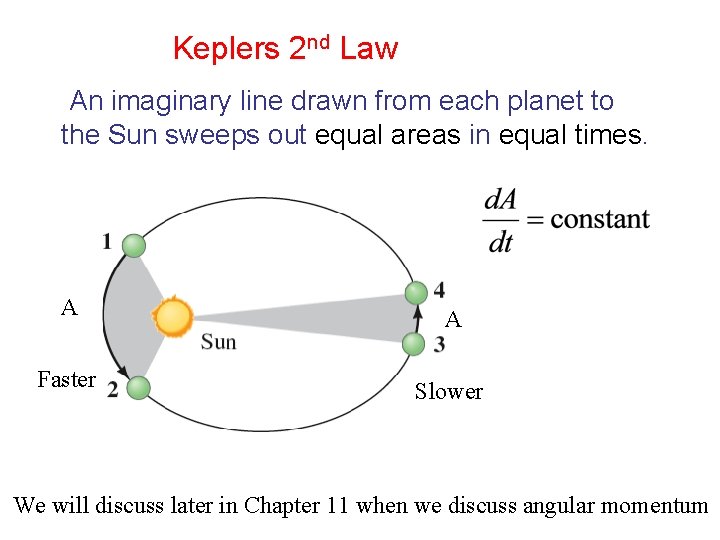
Keplers 2 nd Law An imaginary line drawn from each planet to the Sun sweeps out equal areas in equal times. A A Faster Slower We will discuss later in Chapter 11 when we discuss angular momentum

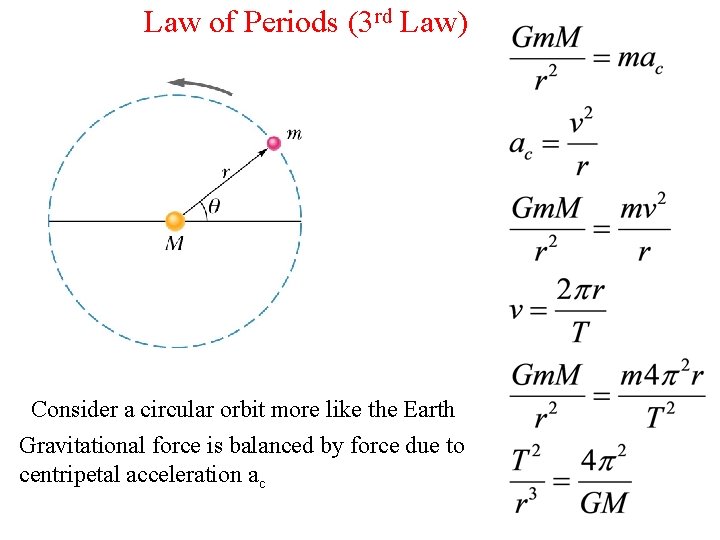
Law of Periods (3 rd Law) Consider a circular orbit more like the Earth Gravitational force is balanced by force due to centripetal acceleration ac

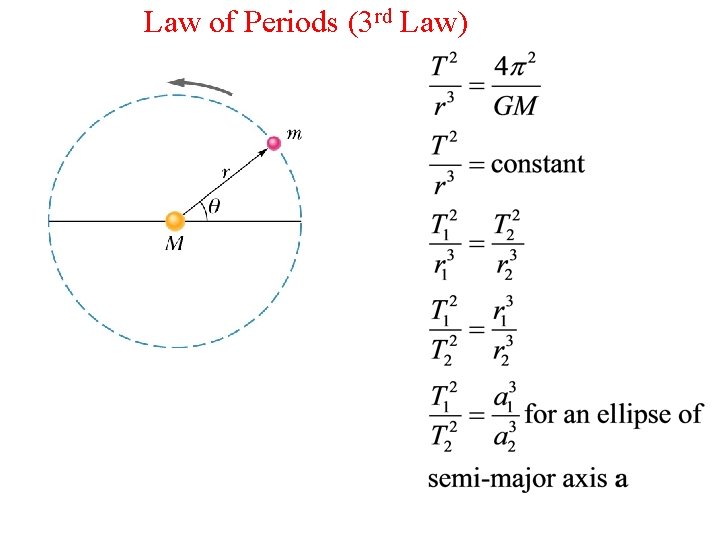
Law of Periods (3 rd Law)

Evidence for the 3 rd Law The square of a planet’s orbital period is proportional to the cube of its mean distance from the Sun.

Websites for Resources and Videos http: //galileoandeinstein. physics. virginia. edu/more_stuff/Applets/home. html http: //galileoandeinstein. physics. virginia. edu/more_stuff/flashlets/home. htm Lets do some problems

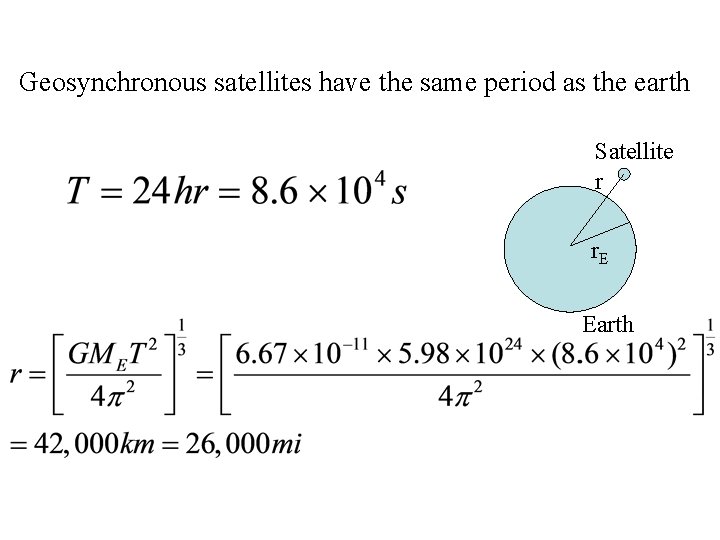
Problem: What is the distance from the Earth’s center for a geosynchronous TV satellite? Satellite r r. E Earth Geosynchronous satellites have the same period as the earth Find r.

Geosynchronous satellites have the same period as the earth Satellite r r. E Earth

Problem: What is the weight of a Satellite in orbit if it weighs 1000 N on Earth?

Problem: What is the net gravitational force on a particle inside the Earth Doesn’t this force remind you of a mass on a spring? What is the resultant motion look like?

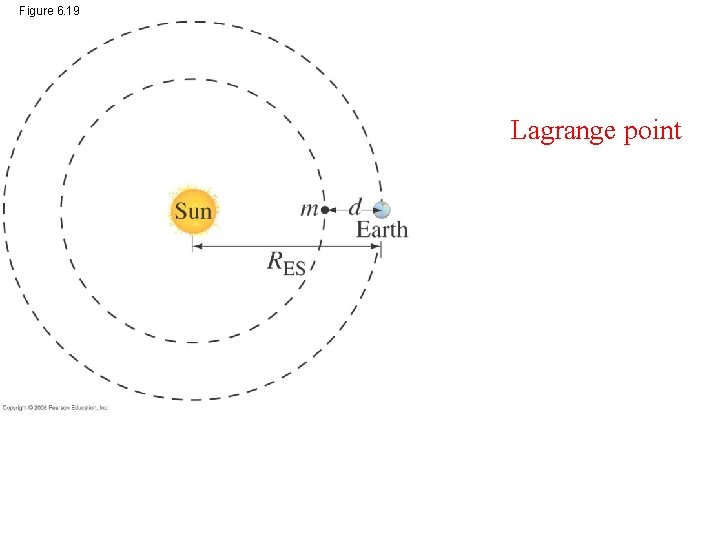
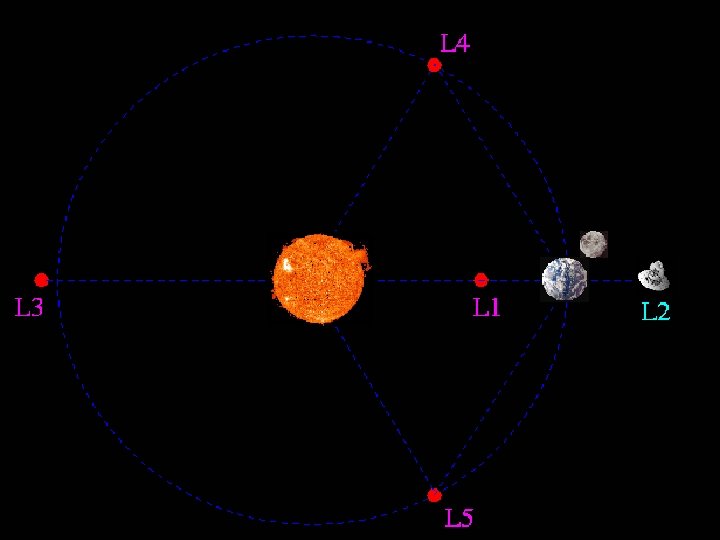
Figure 6. 19 Lagrange point

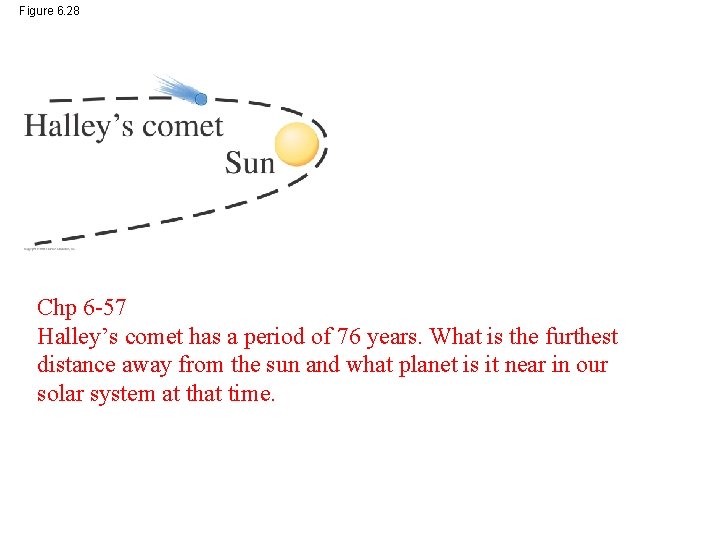
Figure 6. 28 Chp 6 -57 Halley’s comet has a period of 76 years. What is the furthest distance away from the sun and what planet is it near in our solar system at that time.

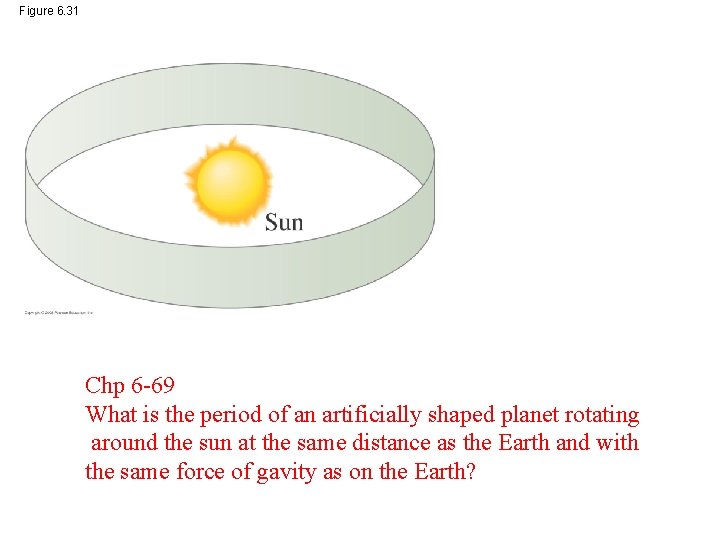
Figure 6. 31 Chp 6 -69 What is the period of an artificially shaped planet rotating around the sun at the same distance as the Earth and with the same force of gavity as on the Earth?

Figure 6. 12 Chp 6 -62 A satellite of mass 5500 kg orbits the earth with a period of 6200 s. a)What is the radius of the orbit? b)What is the gravitational force on it? c)What is the height above the earth?