CHAPTER 6 Fundamental Dimensions and Units 2011 Cengage

CHAPTER 6 Fundamental Dimensions and Units © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -1

Engineering Fundamentals – Concepts Every Engineer Should Know • Fundamental dimensions and units • Length and length-related parameters • Time and time-related parameters • Mass and mass-related parameters • Force and force-related parameters • Temperature and temperature-related parameters • Electric current and related parameters • Energy and power © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -2

Outline In this chapter we will • Explain fundamental dimensions and units • Explain the steps necessary to convert information from one system of units to another • Explain what is meant by an engineering components and systems © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -3

Outline (continued) In this chapter we will • Emphasize the importance of showing appropriate units with all calculations • Discuss how you can learn the engineering fundamental concepts using fundamental dimensions © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -4

Objectives The objectives of this chapter are to • Introduce the fundamental dimensions and units that every engineer should know • Show these fundamental quantities are related to design © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -5

Fundamental Dimensions The physical quantities used to fully describe natural events and our surroundings are: • Length • Temperature • Mass • Amount of substance • Time • Luminous intensity • Electric current © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -6

Units • Used to measure physical dimensions • Appropriate divisions of physical dimensions to keep numbers manageable v 19 years old instead of 612, 000 seconds old • Common systems of units v International System (SI) of Units v British Gravitational (BG) System of Units v U. S. Customary Units © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -7

Units – SI • Most common system of units used in the world • Examples of SI units are: kg, N, m, cm, • Approved by the General Conference on Weights and Measures (CGPM) • Series of prefixes & symbols of decimal multiples (adapted by CGPM, 1960) © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -8

Fundamental Unit of Length meter (m) – length of the path traveled by light in a vacuum during a time interval of 1/299, 792, 458 of a second © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -9

Fundamental Unit of Mass kilogram (kg) – a unit of mass; it is equal to the mass of the international prototype of the kilogram © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -10

Fundamental Unit of Time second (s) – duration of 9, 192, 631, 770 periods of the radiation corresponding to the transition between the 2 hyperfine levels of the ground state of cesium 133 atom © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -11

Fundamental Unit of Electric Current ampere (A) – constant current which, if maintained in 2 straight parallel conductors of infinite length, of negligible circular cross section, and placed 1 meter apart in a vacuum, would produce between these conductors a force equal to 2 x 10 -7 N/m length © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -12

Fundamental Unit of Temperature kelvin (K) – unit of thermodynamic temperature, is the fraction 1/273. 16 of thermodynamic temperature of the triple point of water © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -13

Fundamental Unit of Amount of Substance mole (mol) – the amount of substance of a system that contains as many elementary entities as there atoms in 0. 012 kilogram of carbon 12 © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -14

Fundamental Unit of Luminous Intensity candela (cd) – in a given direction, of a source that emits monochromatic radiation of frequency 540 x 1012 hertz and that has a radiant intensity in that direction of 1/683 watt per steradian © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -15

SI – Prefix & Symbol Adopted by CGPM in 1960 © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -16

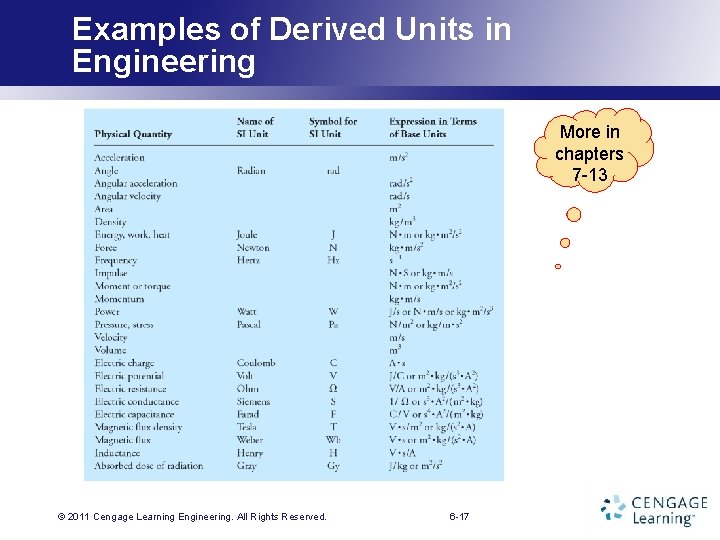
Examples of Derived Units in Engineering More in chapters 7 -13 © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -17

British Gravitation (BG) System More on temperature in chapter 11 • Primary units are v foot (ft) for length (1 ft = 0. 3048 m) v second for time v pound (lb) force (1 lb = 4. 448 N) o v Fahrenheit ( F) for temperature • Slug is unit of mass which is derived from Newton’s second law 2 v 1 lb = (1 slug)(1 ft/s ) © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -18

U. S. Customary System of Units • Primary units are v Foot (ft) for length (1 ft = 0. 3048 m) v second for time v pound mass (lbm) for mass (1 lbm = 0. 453592 kg, 1 slug = 32. 2 lbm) More on derived units in chapters 7 -13 • Pound force (lbf) is defined as the weight of an object having a mass of 1 lbm at sea level and at a latitude of 45 o, where acceleration due to gravity is 32. 2 ft/s 2 (1 lbf = 4. 448 N) © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -19

Examples of SI Units in Everyday Use © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -20

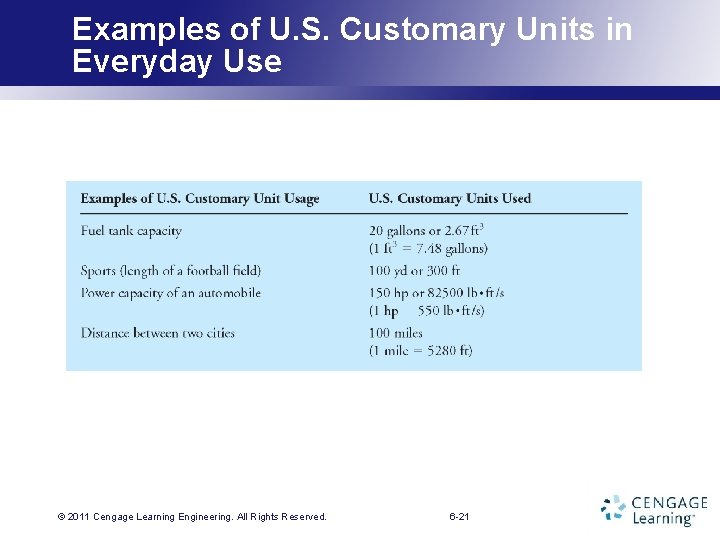
Examples of U. S. Customary Units in Everyday Use © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -21

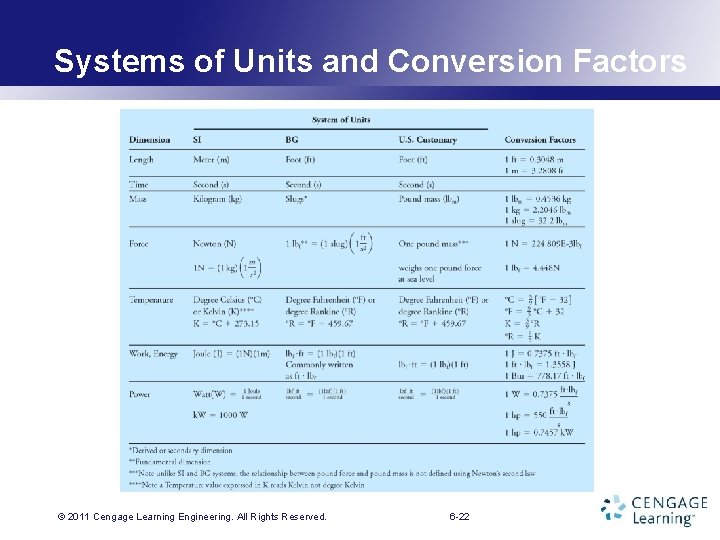
Systems of Units and Conversion Factors © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -22

Unit Conversion • In engineering analysis and design, there may be a need to convert from one system of units to another • When communicate with engineers outside of U. S. • Important to learn to convert information from one system of units to another correctly • Always show the appropriate units that go with your calculations • See the conversion tables given in the book © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -23

Example 6. 1 – Unit Conversion Given: a person who is 6’-1” tall and weighs 185 pound force (lbf) Find: height and weight in SI units Solution: © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -24

Example 6. 1 – Unit Conversion (continued) Given: a person is driving a car at a speed of 65 miles per hour (mph) over a distance of 25 miles Find: speed and distance in SI units Solution: © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -25

Example 6. 1 – Unit Conversion (continued) Given: outside temperature is 80 o. F and has a density of 0. 0735 pound mass per cubic foot (lbm/ft 3) Find: temperature and density in SI units Solution: © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -26

Example 6. 2 – Unit Conversion Given: area A = 100 cm 2 Find: A in m 2 Solution: © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -27

Example 6. 2 – Unit Conversion (continued) Given: volume V = 1000 mm 3 Find: V in m 3 Solution: © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -28

Example 6. 2 – Unit Conversion (continued) Given: atmosphere pressure P = 105 N/m 2 Find: P in lb/in 2 Solution: © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -29

Example 6. 2 – Unit Conversion (continued) Given: density of water = 1000 kg/m 3 Find: density in lbm/ft 3 Solution: © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -30

Examples of Unit Conversion © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -31

Dimension Homogeneity • Given: L = a + b + c • Left hand side of equation should have the same dimension as right hand side of equation • If L represents dimension length, then a, b, and c must also have the dimension of length – this is called dimensionally homogeneous © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -32

Example 6. 3 – Dimension Homogeneity Given: where d = end deflection, in m P = applied load, in N L = length of bar, in m A = cross-sectional area of bar, in m 2 E: modulus of elasticity Find: units for E © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -33

Example 6. 3 – Dimension Homogeneity (continued) Solution: © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -34

Example 6. 3 – Dimension Homogeneity (continued) Given: Where q = heat transfer rate k = thermal conductivity of the solid material in W/m●°C A = area in m 2 T 1 – T 2 = temperature difference, °C L = thickness of the material, m Find: units for q © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -35

Example 6. 3 – Dimension Homogeneity (continued) Solution: © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -36

Example 6. 5 – Numerical Versus Symbolic Solutions Given: hydraulic system shown Find: m 2 Numerical solution: © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -37

Example 6. 5 – Numerical Versus Symbolic Solutions (continued) Given: hydraulic system shown Find: m 2 Symbolic solution: © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -38

Significant Digits (Figures) • Engineers make measurements and carry out calculations • Engineers record the results of measurements and calculations using numbers. • Significant digits (figures) represent (convey) the extend to which recorded or computed data is dependable. © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -39

Significant Digits – How to Record a Measurement Least count – one half of the smallest scale division What should we record for this temperature measurement? 71 ± 1 o. F © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -40

Significant Digits – How to Record a Measurement What should we record for the length? 3. 35 ± 0. 05 in. © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -41

Significant Digits – How to Record a Measurement What should we record for this pressure? 7. 5 ± 0. 5 in. © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -42

Significant Digits • 175, 25. 5, 1. 85, and 0. 00125 each has three significant digits. • The number of significant digits for the number 1500 is not clear. v It could be 2, 3, or 4 3 2 v If recorded as 1. 5 x 10 or 15 x 10 , then 2 significant digits © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -43

Significant Digits – Addition And Subtraction Rules When adding or subtracting numbers, the result of the calculation should be recorded with the last significant digit in the result determined by the position of the last column of digits common to all of the numbers being added or subtracted. For example, 152. 47 + 3. 9 or 132. 853 - 5 156. 37 127. 853 (your calculator will display) 156. 3 127 (however, the result should be recorded this way) © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -44

Significant Digits – Multiplication and Division Rules When multiplying or dividing numbers, the result of the calculation should be recorded with the least number of significant digits given by any of the numbers used in the calculation. For example, 152. 47 × 3. 9 or 152. 47 ÷ 3. 9 594. 633 39. 0948717949 (your calculator will display) 5. 9 x 102 39 © 2011 Cengage Learning. Engineering. All Rights Reserved. (however, the result should be recorded this way) 6 -45

Significant Digits – Examples 276. 34 + 12. 782 289. 12 2955 x 326 9. 63 x 105 © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -46

Rounding Numbers In many engineering calculations, it may be sufficient to record the results of a calculation to a fewer number of significant digits than obtained from the rules we just explained 56. 341 to 56. 34 12852 to 1. 285 x 104 © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -47

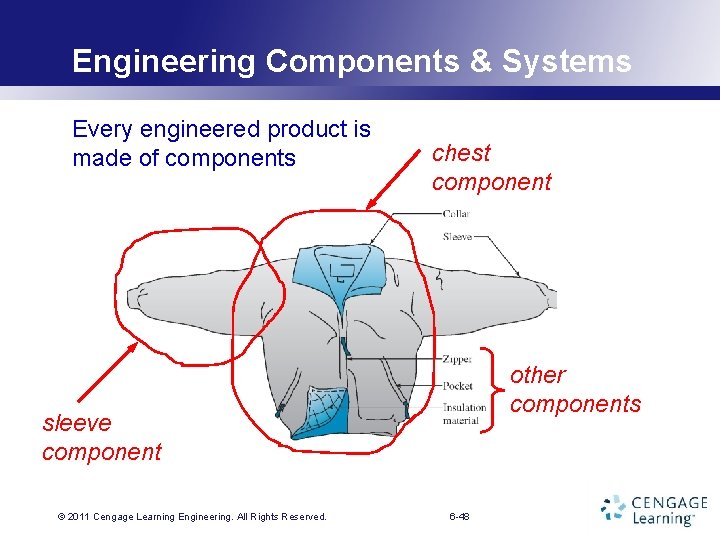
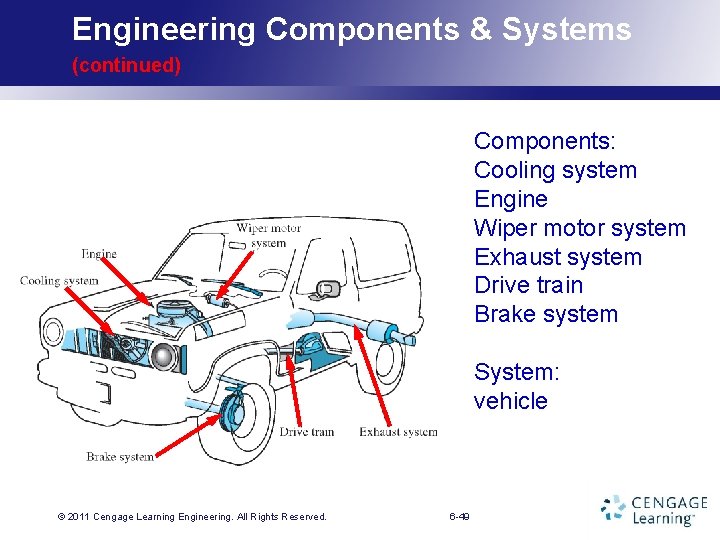
Engineering Components & Systems Every engineered product is made of components chest component other components sleeve component © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -48

Engineering Components & Systems (continued) Components: Cooling system Engine Wiper motor system Exhaust system Drive train Brake system System: vehicle © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -49

Physical Laws and Observations in Engineering • Engineers apply physical and chemical laws and principles along with mathematics to design, develop, test, and produce products and services that we use in our everyday lives • Universe was created in a certain way • We have learned through observation that things work a certain way in nature v For example, if we let go something, it will drop © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -50

Physical Laws and Observations in More in Engineering (continued) thermodynamics course • We use mathematics and basic physical quantities to express our observations in the form of a law • For example, second law of thermodynamics v Heat flows from higher temperature to lower temperature region v When a hot object is placed next to a cold object, the hot object gets cooler and the cold object gets warmer; cold object does not get colder © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -51

Physical Laws and Observations in Engineering (continued) • Engineers are good bookkeepers v For example, conservation of mass § the rate by which mass enters a system minus the rate by which it leaves the system should equal to the rate of increase or decrease of mass within the system v Conservation of energy § Keep track of various forms of energy and how they may change from one form to another © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -52

Physical Laws and Observations in More in Engineering (continued) chapter 10, physics, and dynamics Newton’s second law of motion – there is a direct relationship between the push, mass being pushed, and acceleration of mass © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -53

Physical Laws and Observations in Engineering (continued) • Physical laws are based on observations • Some physical laws may not fully describe all possible situations • Some laws are stated in a particular way to keep the mathematical expression simple • Engineering correlations are based on experimental results and have limited applications © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -54

Learning Engineering Fundamental Concepts and Design Variables from Fundamental Dimensions • In Chapters 7 to 12, we will focus on teaching you some of the engineering fundamentals that you will see over and over in some form or other during your college years. • You should try to study these concepts, that every engineer should know, carefully and understand them completely. • We will focus on an innovative way to teach some of the engineering fundamental concepts using fundamental dimensions. © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -55

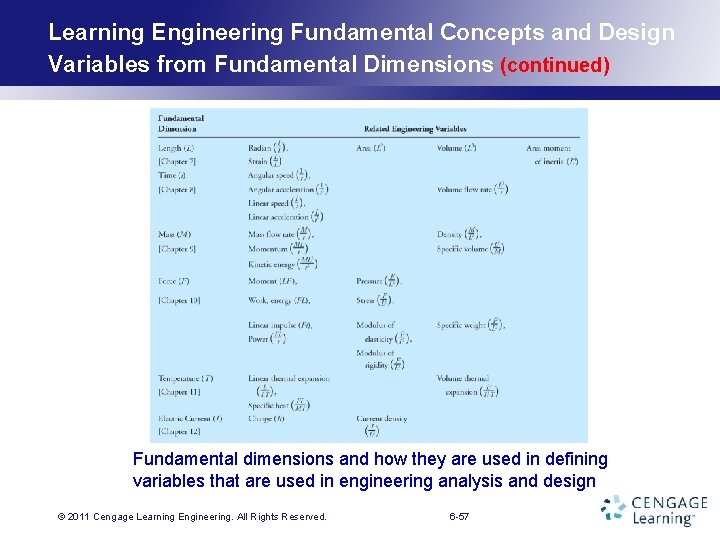
Learning Engineering Fundamental Concepts and Design Variables from Fundamental Dimensions (continued) • We only need a few physical quantities (fundamental dimensions) to describe events and our surroundings. • With the help of these fundamental dimensions, we can define or derive engineering variables that are commonly used in analysis and design. © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -56

Learning Engineering Fundamental Concepts and Design Variables from Fundamental Dimensions (continued) Fundamental dimensions and how they are used in defining variables that are used in engineering analysis and design © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -57

Summary • You should understand the importance of fundamental dimensions in engineering analysis • You should understand what is meant by an engineering system and an engineering component • You should know the most common systems of units • You should know how to convert values from one system of units to another © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -58

Summary (continued) • You should understand the difference between numerical and symbolic solutions • You should know how to present the result of your calculation or measurement using correct number of significant digits © 2011 Cengage Learning. Engineering. All Rights Reserved. 6 -59