Chapter 6 Extensive Games perfect info Detailed description

Chapter 6 Extensive Games, perfect info • Detailed description of the sequential structure of strategic situations – as opposed to Strategic Games • Players perfectly informed of occurred events • Initially decisions are not made at the same time, no randomness

Example 91. 1 / Def. 89. 1 Extensive game: Players to share two objects – Conventional definition with trees as primitives: 1 (2, 0) (1, 1) 2 yes no 2, 0 0, 0 yes 1, 1 (0, 2) 2 no yes 0, 0 0, 2 no 0, 0

– Definition with players´ actions as primitives: • G = (N, H, P, ( i)) • A Set of Players – N = {1, 2} • A Set of possible histories (sequences, finite or infinite) – H = { , (2, 0), (1, 1), (0, 2), ((2, 0), yes), ((2, 0), no), ((1, 1), yes), ((1, 0), no), ((0, 2), yes), ((0, 2), no)} • Terminal histories – Z = {((2, 0), yes), ((2, 0), no), ((1, 1), yes), ((1, 1), no), ((0, 2), yes), ((0, 2), no)} 1 (2, 0) (1, 1) 2 yes no 2, 0 0, 0 yes 1, 1 (0, 2) 2 no yes 0, 0 0, 2 no 0, 0

• A player function that assigns a player to each non terminal history – P( ) = 1 and P(h) = 2 for every non terminal h • A preference relation for each player on Z: – i: ((2, 0), yes) >1 ((1, 1), yes) >1 ((0, 2), yes) ~1 ((2, 0), no) ~1 ((1, 1) ~1 yes) ~1((1, 1), no) and ((2, 0), yes) >2 ((1, 1), yes) >2 ((0, 2), yes) ~2 ((2, 0), no) ~2 ((1, 1) ~2 yes) ~2((1, 1), no) 1 (2, 0) (1, 1) 2 yes no 2, 0 0, 0 yes 1, 1 (0, 2) 2 no yes 0, 0 0, 2 no 0, 0

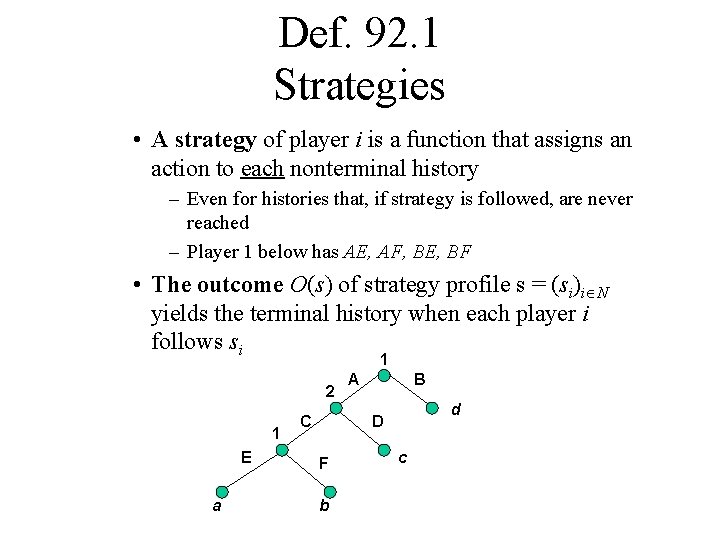
Def. 92. 1 Strategies • A strategy of player i is a function that assigns an action to each nonterminal history – Even for histories that, if strategy is followed, are never reached – Player 1 below has AE, AF, BE, BF • The outcome O(s) of strategy profile s = (si)i N yields the terminal history when each player i follows si 1 2 1 E a C A B d D F b c

Def. 93. 1 Nash Equilibrium • Nash Equilibrium for an extensive game with perfect info is a strategy profile s* such that for every player i N we have – O(s*-i, s*i) i O(s*-i, si) for every strategy si of player i – (If other players follows s* you would better follow s* too. . . ) • Alternatively it is the Nash Equilibrium of a strategic game derived from the extensive game

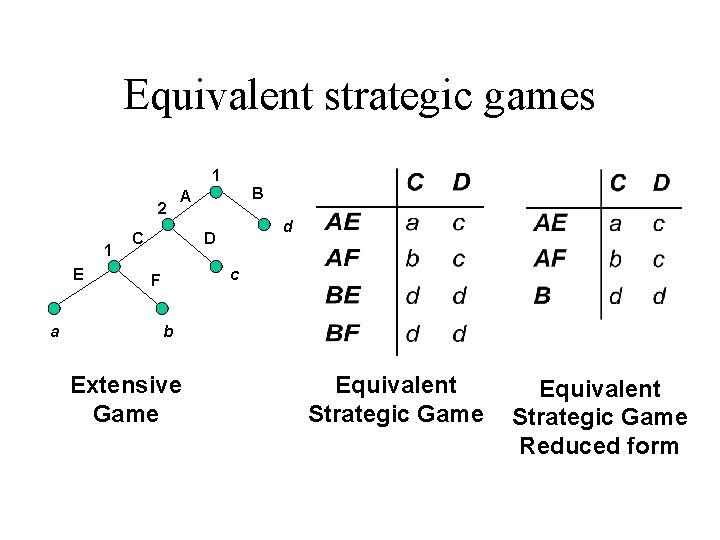
Equivalent strategic games 1 2 1 E a B A C d D c F b Extensive Game Equivalent Strategic Game Reduced form

Example 95. 2 1 2 L 0, 0 B A R 1, 2 2, 1 • Given that player 2 chooses L it is optimal for player 1 to choose B • The Nash equilibrium (B, L) lacks plausibility since P 2 wouldn’t choose L after A.

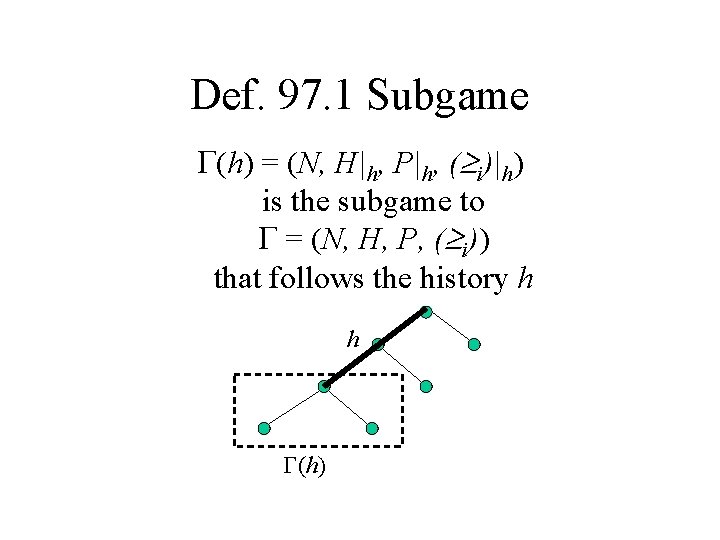
Def. 97. 1 Subgame (h) = (N, H|h, P|h, ( i)|h) is the subgame to = (N, H, P, ( i)) that follows the history h h (h)

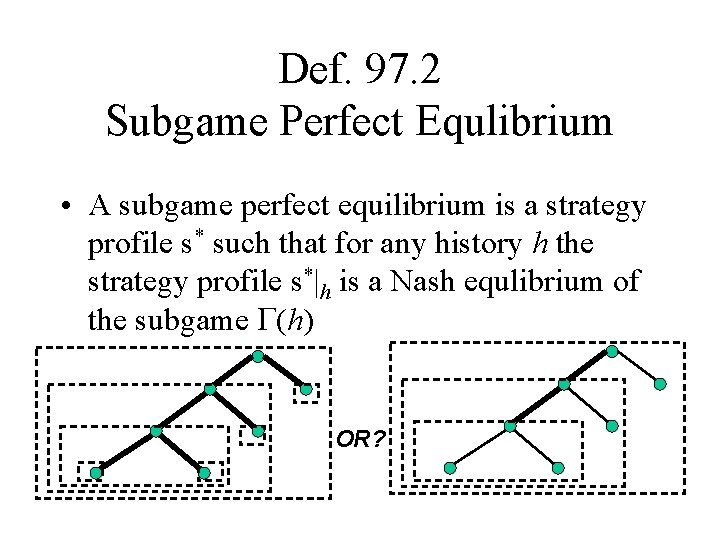
Def. 97. 2 Subgame Perfect Equlibrium • A subgame perfect equilibrium is a strategy profile s* such that for any history h the strategy profile s*|h is a Nash equlibrium of the subgame (h) OR?

Example 95. 2 again 1 2 L 0, 0 B A R 2, 1 1, 2 (A) • (B, L) is a Nash equilibrium • Is (B, L) a subgame perfect equilibrium? – The strategy profile s*|h = (B, L)|A in the subgame (A) is for instance no Nash Equilibrium – Player 2 wouldn’t chose L given that player 1 has chosen A

Prop. 99. 2 Kuhn´s Theorem • Every finite extensive game with perfect info has a subgame perfect equilibrium. – E. g chess is draw once a position is repeated three times => chess is finite

Two Extensions to Extensive Games with perfect info • Exogenous uncertainty – The Player function P(h) has a probability that chance determines the action after the history h – Definition of a subgame perfect equilibrium and Kuhn’s theorem still OK • Simultaneous moves – The Player function P(h) assigns a set of players that make choices after the history h

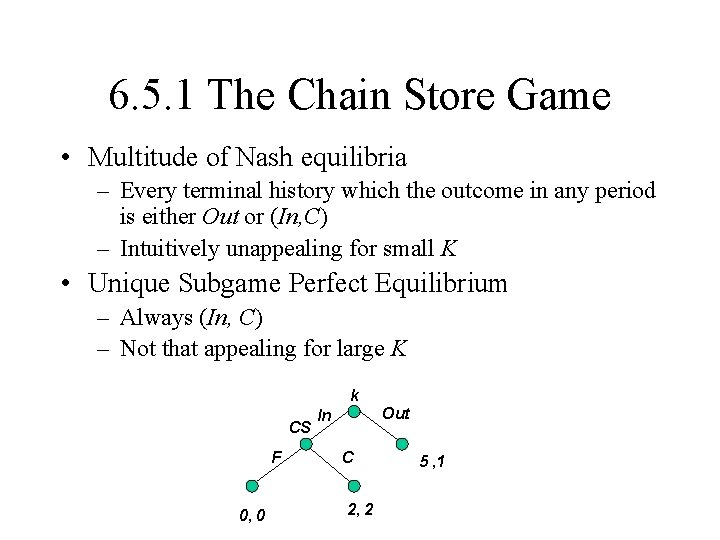
6. 5. 1 The Chain Store Game • Multitude of Nash equilibria – Every terminal history which the outcome in any period is either Out or (In, C) – Intuitively unappealing for small K • Unique Subgame Perfect Equilibrium – Always (In, C) – Not that appealing for large K k CS F 0, 0 Out In C 2, 2 5 , 1

Ex. 110. 1 Bo. S with an outside option • Elimination of dominated actions yields: (B, B) • Interpretation – BB >1 Book >1 SS >1 BS ~1 SB – Player 2 knows that if player 1 selects concert he would choose Bach otherwise he would better stay home reading the book – Thus player 1 can select B knowing that player 2 also selects B 1 Book 2, 2 Concert

Ex. 111. 1 Burning money – Elimination of dominated actions yields: (0 B, BB) – Interpretation: • P 2 thinks that if P 1 spends D then he wants to go Bach otherwise he would loose compared to not spending D => P 2 chooses B if P 1 chooses D • P 1 knows this and can expect a payoff of 2 by choosing DB • P 2 knows that the rationality of P 1 choosing 0 is that he expects to gain better than 2 (by choosing DB) • Thus P 1 can choose 0 B and gain 3 – Authors think that this example is implausible 1 0 D