Chapter 6 Energy and Work Chapter Goal To

Chapter 6. Energy and Work Chapter Goal: To develop an understanding of mechanical energy; its transfer to and from a system through work, its transformation within the system, and its conservation.

Ch. 6 – Student Learning Objectives • To begin developing a concept of energy— what it is, how it is transformed, and how it is transferred. • To introduce the concepts of kinetic and potential energy. • To introduce work as an energy transfer mechanism.

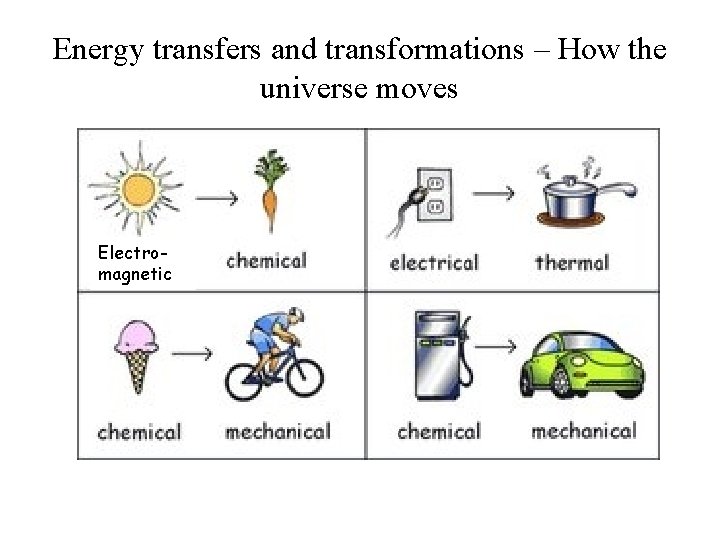
Energy transfers and transformations – How the universe moves Electromagnetic

Conservation of Mechanical Energy – The Big Picture Two basic types of mechanical energy: • Kinetic energy (K) is an energy of motion. • Gravitational potential energy U (GPE in our text) is an energy of position in a gravitational field. Under some circumstances (e. g. freefall) these two kinds of energy can be transformed back and forth without loss from the system. Kinetic energy of the system can change to gravitational potential energy (U) and vice versa

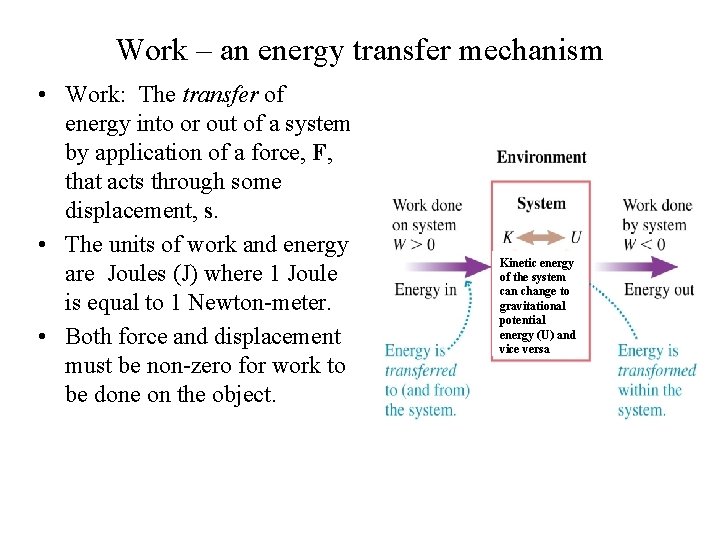
Work – an energy transfer mechanism • Work: The transfer of energy into or out of a system by application of a force, F, that acts through some displacement, s. • The units of work and energy are Joules (J) where 1 Joule is equal to 1 Newton-meter. • Both force and displacement must be non-zero for work to be done on the object. Kinetic energy of the system can change to gravitational potential energy (U) and vice versa

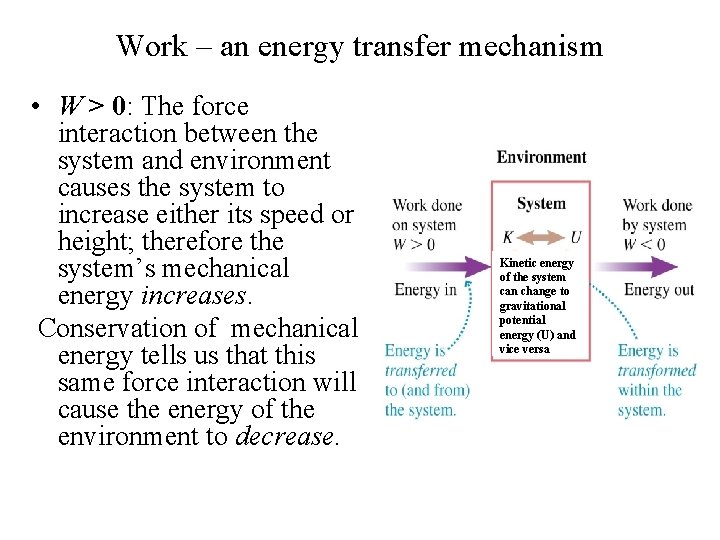
Work – an energy transfer mechanism • W > 0: The force interaction between the system and environment causes the system to increase either its speed or height; therefore the system’s mechanical energy increases. Conservation of mechanical energy tells us that this same force interaction will cause the energy of the environment to decrease. Kinetic energy of the system can change to gravitational potential energy (U) and vice versa

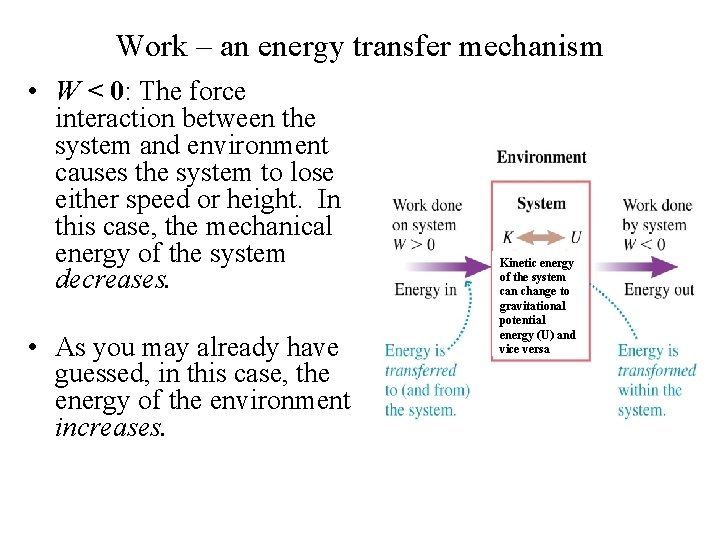
Work – an energy transfer mechanism • W < 0: The force interaction between the system and environment causes the system to lose either speed or height. In this case, the mechanical energy of the system decreases. • As you may already have guessed, in this case, the energy of the environment increases. Kinetic energy of the system can change to gravitational potential energy (U) and vice versa

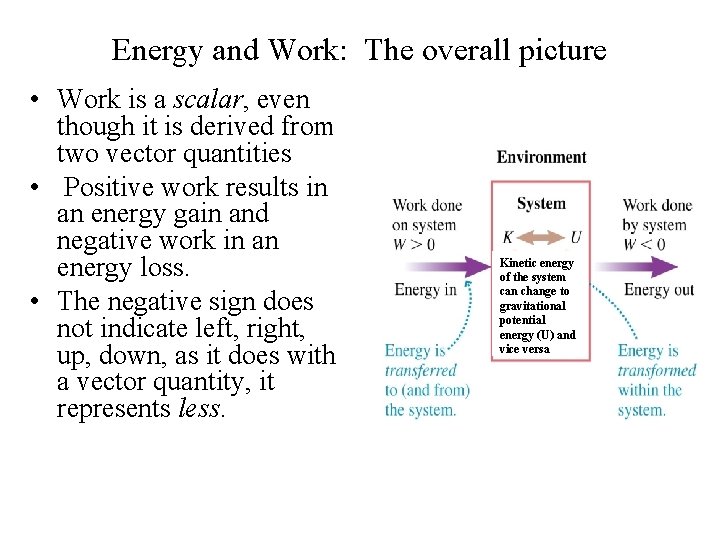
Energy and Work: The overall picture • Work is a scalar, even though it is derived from two vector quantities • Positive work results in an energy gain and negative work in an energy loss. • The negative sign does not indicate left, right, up, down, as it does with a vector quantity, it represents less. Kinetic energy of the system can change to gravitational potential energy (U) and vice versa

Work done by a constant force • Consider our system to consist of the suitcase. The rest of the universe (and especially the woman) is the environment. By pulling on the suitcase with a force, F, the environment increases the energy, (specifically the kinetic energy) of the suitcase. • Now let’s calculate the work done by the pulling force on the suitcase.

Work done by a constant force W = |F| |s| cos θ • F and s are, respectively, the magnitudes of the force and displacement vectors, • θ is the angle (not necessarily acute) between the force vector and the displacement vector when they are tail to tail. • This is the work due to the pulling force only.

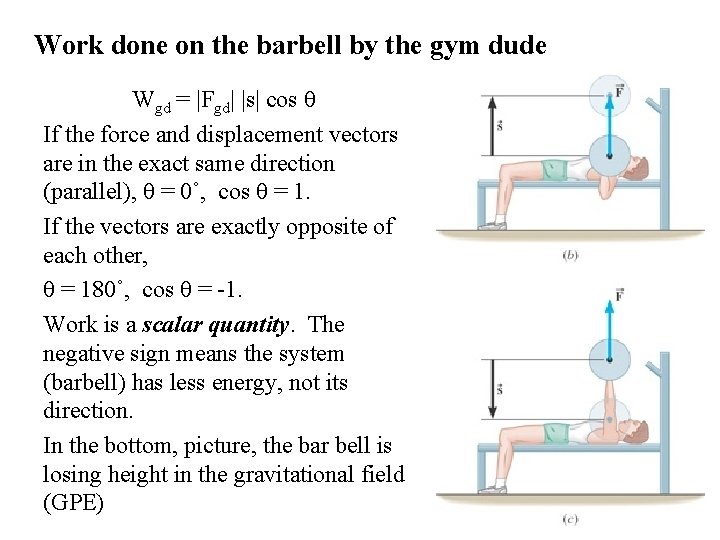
Work done on the barbell by the gym dude Wgd = |Fgd| |s| cos θ If the force and displacement vectors are in the exact same direction (parallel), θ = 0˚, cos θ = 1. If the vectors are exactly opposite of each other, θ = 180˚, cos θ = -1. Work is a scalar quantity. The negative sign means the system (barbell) has less energy, not its direction. In the bottom, picture, the bar bell is losing height in the gravitational field (GPE)

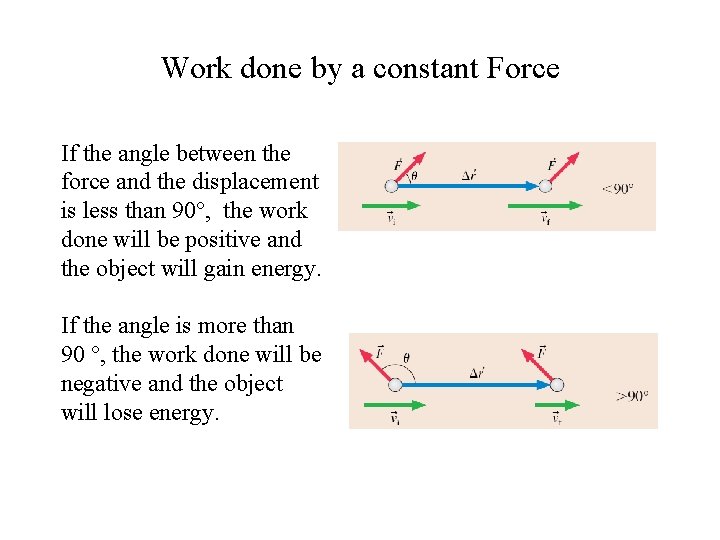
Work done by a constant Force If the angle between the force and the displacement is less than 90°, the work done will be positive and the object will gain energy. If the angle is more than 90 °, the work done will be negative and the object will lose energy.

Work has its ups and downs, but is it positive or negative? A crane lowers a steel beam into place at a construction site. The beam moves with constant speed. Consider the work Wg done by gravity and the work WT done by the tension in the cable. Which of the following is correct and why? A. B. C. D. E. WG and WT are both zero. WG is negative and WT is negative. WG is negative and WT is positive. WG is positive and WT is negative. T FG Δs

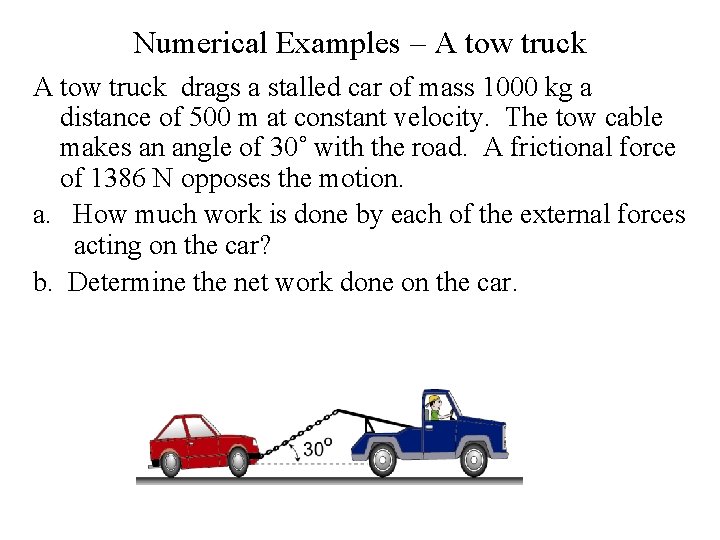
Numerical Examples – A tow truck drags a stalled car of mass 1000 kg a distance of 500 m at constant velocity. The tow cable makes an angle of 30˚ with the road. A frictional force of 1386 N opposes the motion. a. How much work is done by each of the external forces acting on the car? b. Determine the net work done on the car.

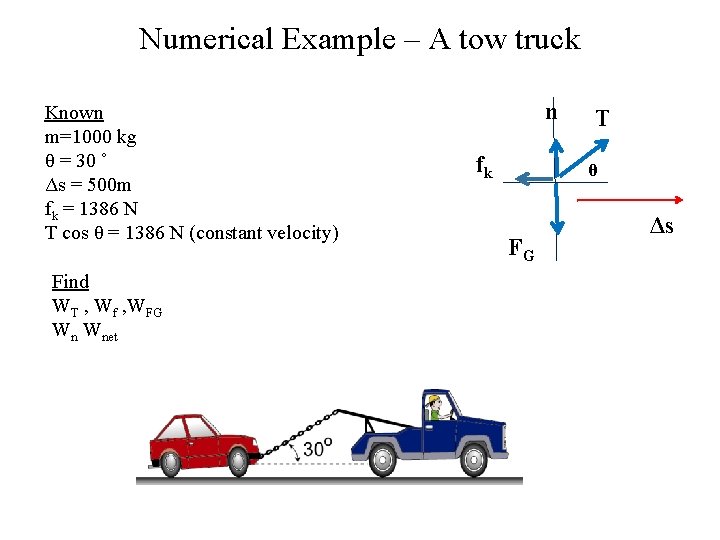
Numerical Example – A tow truck Known m=1000 kg θ = 30 ˚ Δs = 500 m fk = 1386 N T cos θ = 1386 N (constant velocity) Find WT , Wf , WFG Wn Wnet n fk T θ FG Δs

Numerical Example – A tow truck T = 1386 N / cos θ = 1600 N WT = TΔs cos θ WT = (1600 N)(500 m) cos 30˚ WT = 6. 93 x 105 Joules WFG = Wn = 0 (cos 90°!) Wf = (1386 N)(500) cos 180˚ Wf = - 6. 93 x 105 Joules Wnet = 0 (car gains neither speed nor height, so we would expect that). n fk T θ FG Known m=1000 kg θ = 30 ˚ Δs = 500 m fk = 1386 N Find T, WT , Wf WFG , Wn Wnet Δs

Numerical Example – #9 – elevator going down An elevator has a mass of 6020 kg. It travels 6. 0 m down to the next floor. The tension in the cable exerts a force of 70, 000 N on the elevator. a. How much work is done by each of the external forces acting on the elevator? b. Determine the net work done on the elevator. T FG Δs

Numerical Example – #9 – elevator going down T WFG = FG Δs cos θ WT = TΔs cos θ Wnet = WT + WG Known m=6020 kg Δs = 6. 0 m T = 70, 000 N FG Δs

Numerical Example – #9 – elevator going down T WFG = FG Δs cos 0° = 3. 54 x 105 J WT = TΔs cos 180 ° = -4. 20 x 105 J Wnet = WT + WG = -6. 60 x 104 J FG Known m=6020 kg Δs = 6. 0 m T = 70, 000 N Δs

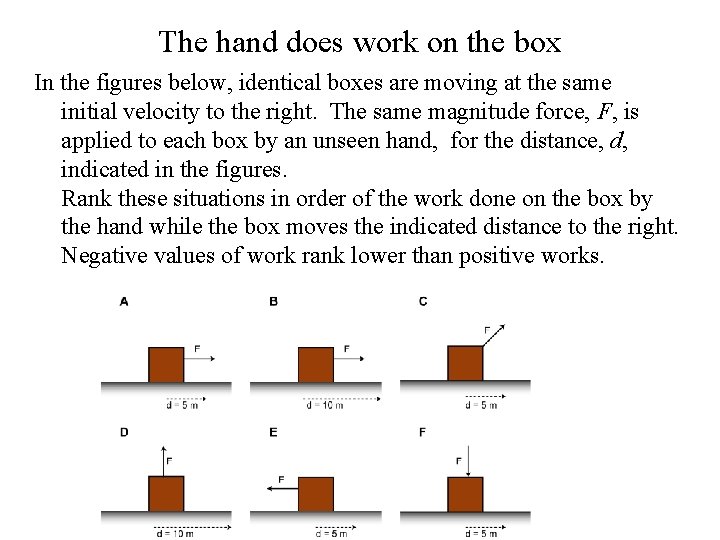
The hand does work on the box In the figures below, identical boxes are moving at the same initial velocity to the right. The same magnitude force, F, is applied to each box by an unseen hand, for the distance, d, indicated in the figures. Rank these situations in order of the work done on the box by the hand while the box moves the indicated distance to the right. Negative values of work rank lower than positive works.

The box does work on the hand In the figures below, identical boxes of mass 10 kg are moving at the same initial velocity to the right on a flat surface. The same magnitude force, F, is applied by a hand to each box for the distance, d, indicated in the figures. Rank these situations in order of the work done by the box on the hand exerting the force F while the box moves the indicated distance to the right. Negative work rank lower than positive work.

The Work-Energy Theorem (in its simplest expression) • Kinetic energy is energy of motion: K = ½ mv 2. • The work done on a system adds kinetic energy to or takes it away from the system. The Work-Energy Theorem expresses that as: W = ΔK We will consider gravitational potential energy shortly. Kinetic energy of the system can change to gravitational potential energy (U) and vice versa

Work-Kinetic Energy Theorem. Expanding the statement W = ∆K: |F| |s| cos θ = ½ mvf 2 – ½ mv 02

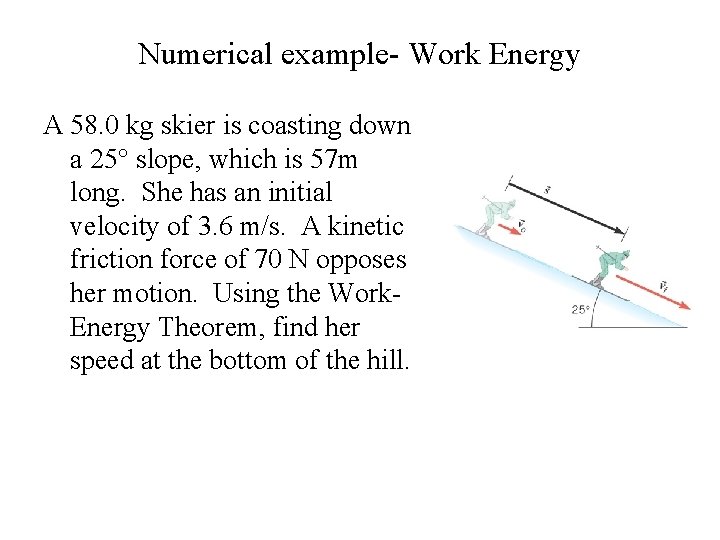
Numerical example- Work Energy A 58. 0 kg skier is coasting down a 25° slope, which is 57 m long. She has an initial velocity of 3. 6 m/s. A kinetic friction force of 70 N opposes her motion. Using the Work. Energy Theorem, find her speed at the bottom of the hill.

Numerical example- Work Energy • Instead of using Newton’s 2 nd law and then kinematics to solve this problem, we will analyze it from the perspective of work and energy. • 1. Draw a free body diagram and list knowns and quantities to find. • 2. Find the work due to all the external forces and solve for net work. • 3. Use the Work Energy Theorem to solve:

Numerical Example no work due to normal force Wf = 70 N x cos 180° x 57 m = -3990 J WG = 568. 4 N x [cos (65°) or sin (25°)] x 57 m = 13682 J Wnet = 9692 J Work-Energy Theorem: (½ mv 2)0 + Wnet = (½ mv 2)1 2(½ mv 20 + Wnet)/m = v 12 [(58 kg)(13 m 2/s 2) + 19384 J] / 58 kg = v 12 v 1 = 18. 6 m/s speed is found in one step. No need to do a Newton’s Law analysis and a kinematics analysis. 65 knowns find: v 1 m= 58 kg v 0 = 3. 6 m/s x 0 = 0 m x 1 = 57 m fk = 70 N θ (incline) = 25° w = mg = 568 N

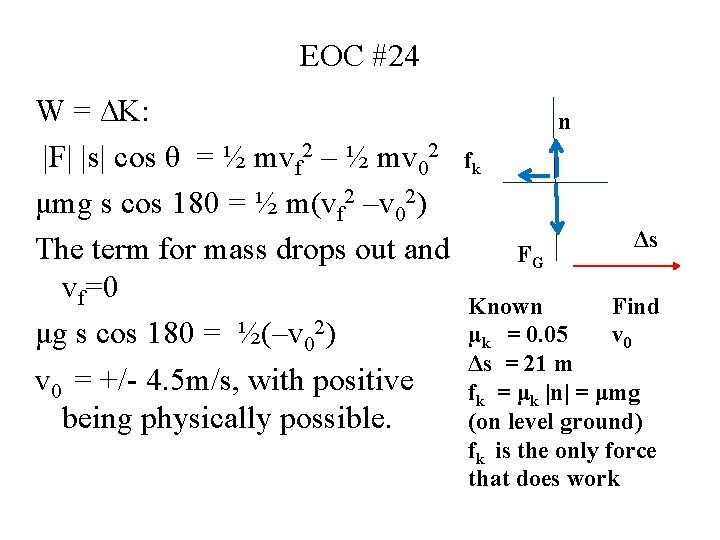
EOC #24 • A skier slides horizontally along the snow for a distance of 21 m before coming to rest. The coefficient of kinetic friction between skier and snow is 0. 050. Initially, how fast was the skier going? (mass isn’t given).

EOC #24 W = ∆K: |F| |s| cos θ = ½ mvf 2 – ½ mv 02 μmg s cos 180 = ½ m(vf 2 –v 02) The term for mass drops out and vf=0 μg s cos 180 = ½(–v 02) v 0 = +/- 4. 5 m/s, with positive being physically possible. n fk FG Δs Known Find µk = 0. 05 v 0 Δs = 21 m fk = μk |n| = μmg (on level ground) fk is the only force that does work

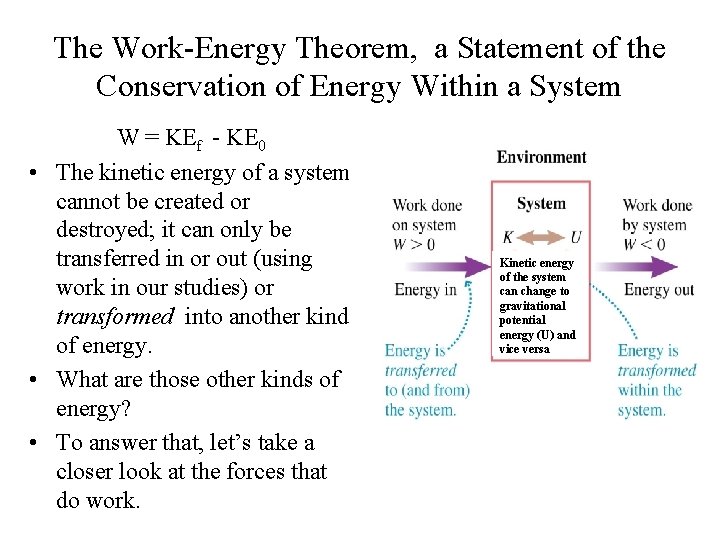
The Work-Energy Theorem, a Statement of the Conservation of Energy Within a System W = KEf - KE 0 • The kinetic energy of a system cannot be created or destroyed; it can only be transferred in or out (using work in our studies) or transformed into another kind of energy. • What are those other kinds of energy? • To answer that, let’s take a closer look at the forces that do work. Kinetic energy of the system can change to gravitational potential energy (U) and vice versa

Conservative vs Non-conservative Forces • conservative force – a force is conservative when the work it does on a moving object does not depend on the path between the object’s initial and final position. – the only conservative forces studied this class is the gravitational force – non-conservative forces include friction, tension, propulsion forces, air resistance (in fact, everything else!).

The Work-Energy Theorem, a Statement of the Conservation of Energy Within a System • Wc - the work done by conservative forces • Wnc - the work done by non-conservative forces Rewrite the Work Energy Theorem as: Wc + Wnc = KEf - KE 0 Since FG is the only conservative force we will study, Wc is the work done by gravity: WG + Wnc = KEf - KE 0

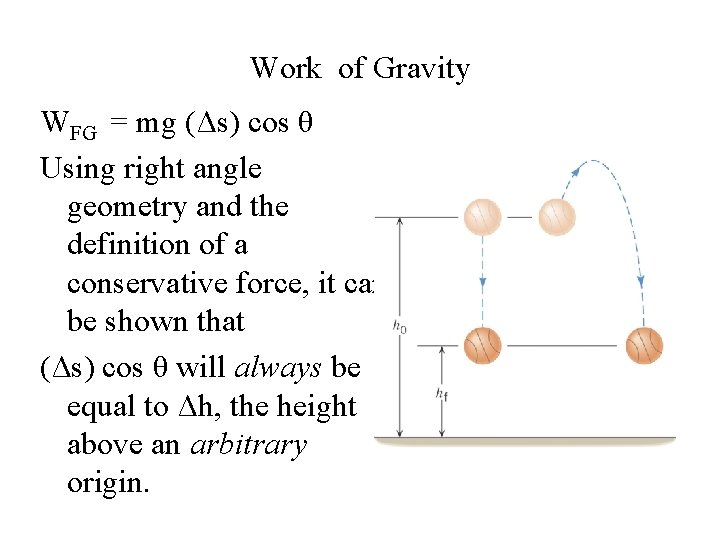
Work of Gravity WFG = mg (Δs) cos θ Using right angle geometry and the definition of a conservative force, it can be shown that (Δs) cos θ will always be equal to Δh, the height above an arbitrary origin.

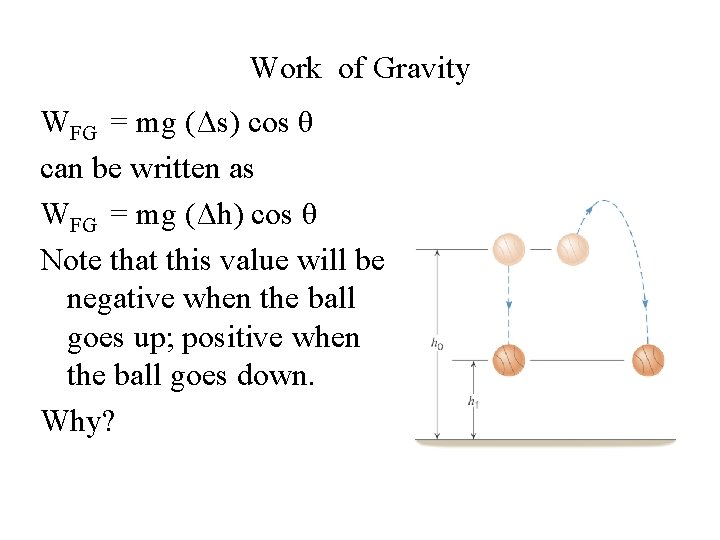
Work of Gravity WFG = mg (Δs) cos θ can be written as WFG = mg (Δh) cos θ Note that this value will be negative when the ball goes up; positive when the ball goes down. Why?

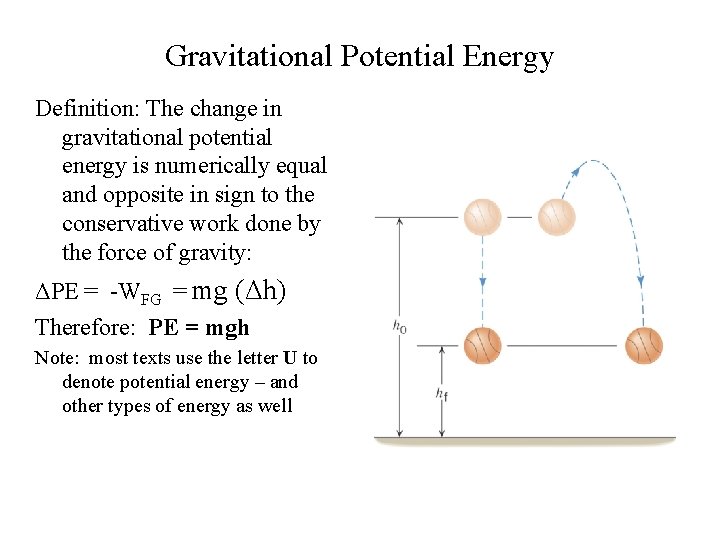
Gravitational Potential Energy Definition: The change in gravitational potential energy is numerically equal and opposite in sign to the conservative work done by the force of gravity: ΔPE = -WFG = mg (Δh) Therefore: PE = mgh Note: most texts use the letter U to denote potential energy – and other types of energy as well

Wnc + Wc = ΔK – (first version of the Work Energy Theorem) Wnc = ΔK – Wc but Wc = -ΔPE , so Wnc = ΔK + ΔPE • Any change in either the kinetic energy or the potential energy of an object occurs because work (either positive or negative) is done on the object. • If no work is done on the object, any change in one type of energy must be balanced by a corresponding change in the other type.

Work Energy Theorem Wnc = ΔK + ΔPE can be written as: Wnc = K - K 0 + PE - PE 0 • I like to rearrange this so it’s in “chronological order”: K 0 + PE 0 + Wnc = K + PE or ½ mv 02 + mgh 0 + |F||s| cos θ = ½ mv 2 + mgh • Initial mechanical energy plus work done equals final mechanical energy • The work due to gravity has been replaced by the change in PE, so don’t use both in one problem: WG = - ΔPE

Conservation of Mechanical Energy If the Wnc = 0 then the mechanical energy of the object will not change and therefore is conserved: K 0 + PE 0 = K + PE If the Wnc ≠ 0, then mechanical energy is not conserved for the object (it just got transferred to/from another object)

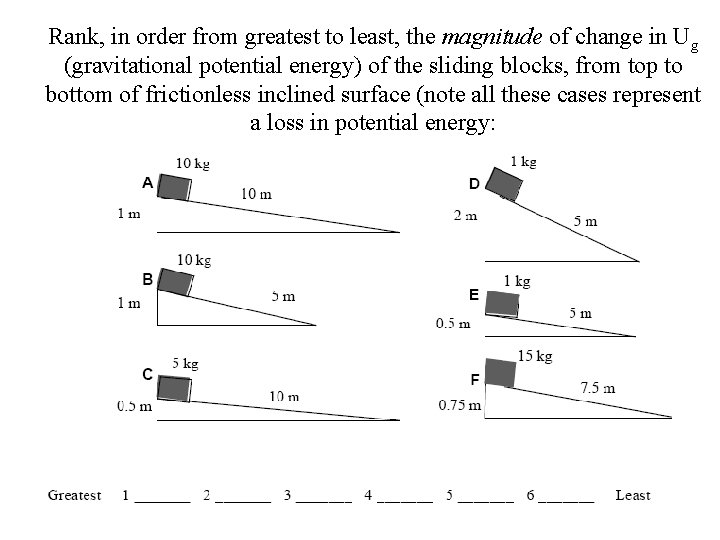
Rank, in order from greatest to least, the magnitude of change in Ug (gravitational potential energy) of the sliding blocks, from top to bottom of frictionless inclined surface (note all these cases represent a loss in potential energy:

Reasoning Strategy - Work-Energy problems • Draw a free body diagram and use Newton’s 2 nd Law to determine the value of external forces doing non-conservative work. • Draw a modified pictorial representation with an origin to identify values for K, PE, if necessary. • List knowns and quantities to find. • Use the Work Energy Theorem modified for the problem • Recall h = ∆s sin θ for inclined slopes

EOC # 35 A 55. 0 kg skateboarder starts out with a speed of 1. 80 m/s. He does +80. 0 J of work on himself by pushing with his feet against the ground. In addition, friction does -265 J of work on him. In both cases, the forces doing the work are nonconservative. The final speed of the skateboarder is 6. 00 m/s. a. Calculate ΔPE b. how much has the vertical height changed?

EOC #83 A basketball of mass 0. 60 kg is dropped from rest from a height of 1. 05 m. It rebounds to a height of 0. 57 m. (a) How much mechanical energy was lost during the collision with the floor? (b) A basketball player dribbles the ball from a height of 1. 05 m by exerting a constant downward force on it for a distance of 0. 080 m. In dribbling, the player compensates for the mechanical energy lost during each bounce. If the ball now returns to a height of 1. 05 m, what is the magnitude of the force?

6. 7 Power • Power is the rate at which energy is transformed or transferred: • Work is an energy transfer mechanism. The work done on an object results in a change in its energy: W = ΔE • Therefore we can say:

Example A man pushed a crate 10 m with a 10 N force in the direction of motion. In which case did he use the most power? A. He pushed it for 1 s B. He pushed it for 10 s C. He pushed it for 0. 1 s D. The amount of time doesn’t matter; they are all the same power.

Another darn ratio problem (FC#25) The power needed to accelerate a projectile from rest to its launch speed v in a time t is P. By what factor does P change if the same projectile is accelerated from rest to a launch speed of 2 v in a time of ½ t? Assume no change in height during this time. a. Increases by a factor of 2 b. Increases by a factor 4 c. Increases by a factor of 8 d. Stays the same; increase in v offset by decrease in time.

Another darn ratio problem (FC#25) The power needed to accelerate a projectile from rest to its launch speed v in a time t is P. By what factor does P change if the same projectile is accelerated from rest to a launch speed of 2 v in a time of ½ t? Assume no change in height. a. Increases by a factor of 2 b. Increases by a factor 4 c. Increases by a factor of 8 d. Stays the same; increase in v offset by decrease in time. Since the initial kinetic energy is zero

Another darn ratio problem (FC#25) The power needed to accelerate a projectile from rest to its launch speed v in a time t is P. By what factor does P change if the same projectile is accelerated from rest to a launch speed of 2 v in a time of ½ t? Assume no change in height. a. Increases by a factor of 2 b. Increases by a factor 4 c. Increases by a factor of 8 d. Stays the same; increase in v offset by decrease in time. The ratio of power in case 2 to that in case one is: