Chapter 6 Elasticity and Demand Mc GrawHillIrwin Copyright

Chapter 6: Elasticity and Demand Mc. Graw-Hill/Irwin Copyright © 2011 by the Mc. Graw-Hill Companies, Inc. All rights reserved.

Elasticity 6 -2

Price Elasticity of Demand (E) • Measures responsiveness or sensitivity of consumers to changes in the price of a good • P & Q are inversely related by the law of demand so E is always negative • The larger the absolute value of E, the more sensitive buyers are to a change in price 6 -3

Sign of Price Elasticity of Demand • The coefficient of the price elasticity of demand is always negative • It is intuitively more appealing to talk about price elasticity in terms of its absolute value. 6 -4

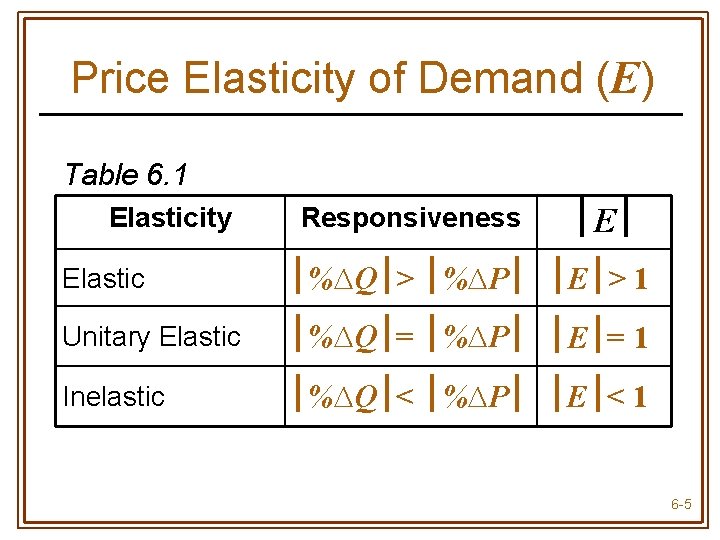
Price Elasticity of Demand (E) Table 6. 1 Elasticity Responsiveness E Elastic %∆Q > %∆P E > 1 Unitary Elastic %∆Q = %∆P E = 1 Inelastic %∆Q < %∆P E < 1 6 -5

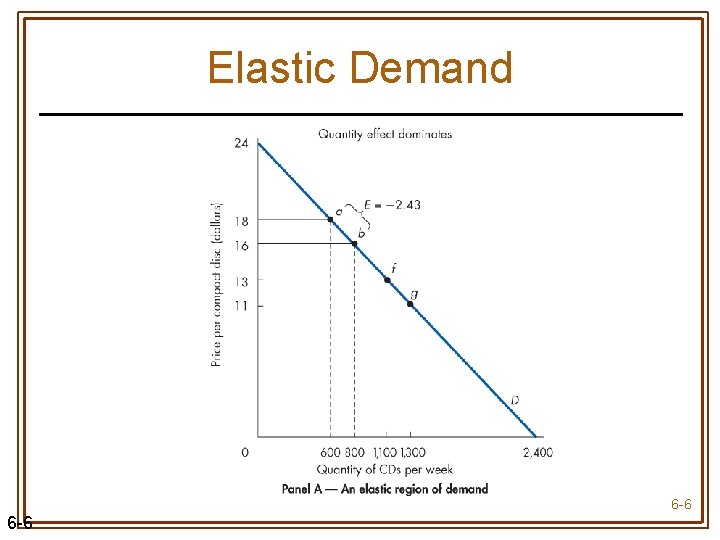
Elastic Demand 6 -6

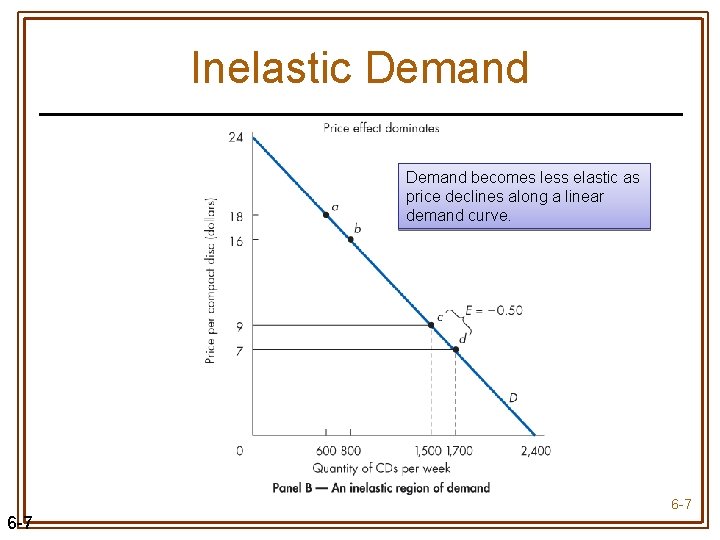
Inelastic Demand becomes less elastic as price declines along a linear demand curve. 6 -7

Price Elasticity of Demand (E) • Percentage change in quantity demanded can be predicted for a given percentage change in price as: • % Qd = % P x E • Percentage change in price required for a given change in quantity demanded can be predicted as: • % P = % Qd ÷ E 6 -8

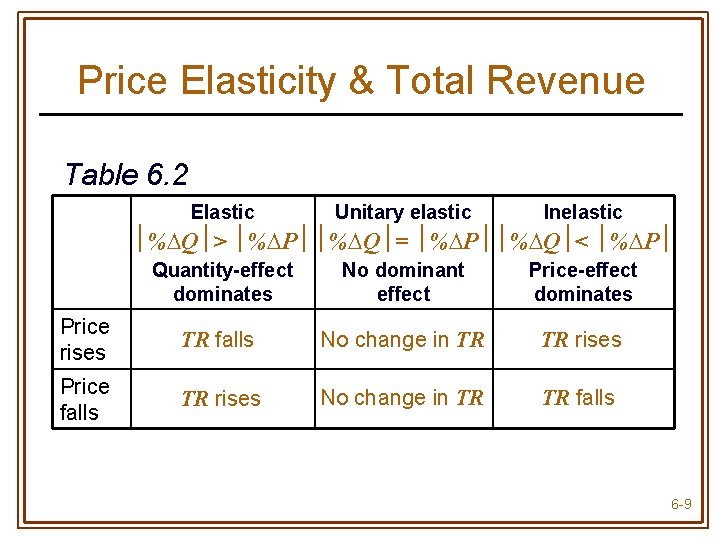
Price Elasticity & Total Revenue Table 6. 2 Elastic Unitary elastic Inelastic %∆Q > %∆P %∆Q = %∆P %∆Q < %∆P Quantity-effect dominates No dominant effect Price-effect dominates Price rises TR falls No change in TR TR rises Price falls TR rises No change in TR TR falls 6 -9

Factors Affecting Price Elasticity of Demand • Availability of substitutes • The better & more numerous the substitutes for a good, the more elastic is demand • Percentage of consumer’s budget • The greater the percentage of the consumer’s budget spent on the good, the more elastic is demand • Time period of adjustment • The longer the time period consumers have to adjust to price changes, the more elastic is demand 6 -10

Factors Affecting Price Elasticity of Demand • Necessities versus Luxuries • Luxuries have a more elastic demand • Definition of the market • The more finely defined the market the more elastic the demand. The more aggregate the definition of the market the more inelastic the demand hamburger < beef <all meat products 6 -11

Calculating Price Elasticity of Demand • Price elasticity can be calculated by multiplying the slope of demand ( Q/ P) times the ratio of price to quantity (P/Q) 6 -12

Calculating Price Elasticity of Demand • Price elasticity can be measured at an interval (or arc) along demand, or at a specific point on the demand curve • If the price change is relatively small, a point calculation is suitable • If the price change spans a sizable arc along the demand curve, the interval calculation provides a better measure 6 -13

Calculating Price Elasticity of Demand • Regression analysis provides a point estimate • Arc elasticity is typically only used for teaching purposes 6 -14

Computation of Elasticity Over an Interval • When calculating price elasticity of demand over an interval of demand, use the interval or arc elasticity formula 6 -15

Computation of Elasticity at a Point • When calculating price elasticity at a point on demand, multiply the slope of demand ( Q/ P), computed at the point of measure, times the ratio P/Q, using the values of P and Q at the point of measure • Method of measuring point elasticity depends on whether demand is linear or curvilinear 6 -16

Price Elasticity for Linear Demand 6– 17 6 -17

Point Elasticity When Demand is Linear • Given Q = a + b. P + c. M + d. PR, let income & price of the related good take specific values M and PR , respectively • Then express demand as Q = a′ + b. P , where a′ = a + c. M + d. PR and the slope parameter is b = ∆Q ∕ ∆P 6 -18

Point Elasticity When Demand is Linear • Compute elasticity using either of the two formulas below which give the same value for E Where P and Q are values of price and quantity demanded at the point of measure along demand, and A ( = –a′ ∕ b) is the price-intercept of demand 6 -19

Point Elasticity When Demand is Curvilinear • Compute elasticity using either of two equivalent formulas below Where ∆Q ∕ ∆P is the slope of the curved demand at the point of measure, P and Q are values of price and quantity demanded at the point of measure, and A is the priceintercept of the tangent line extended to cross the price axis 6 -20

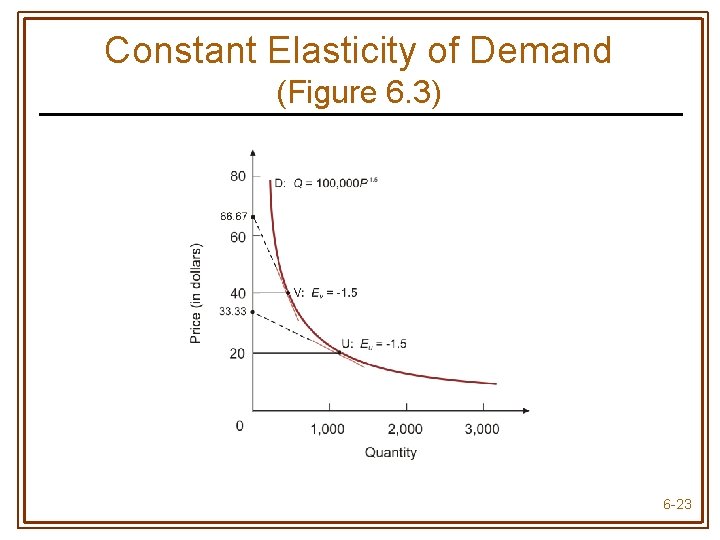
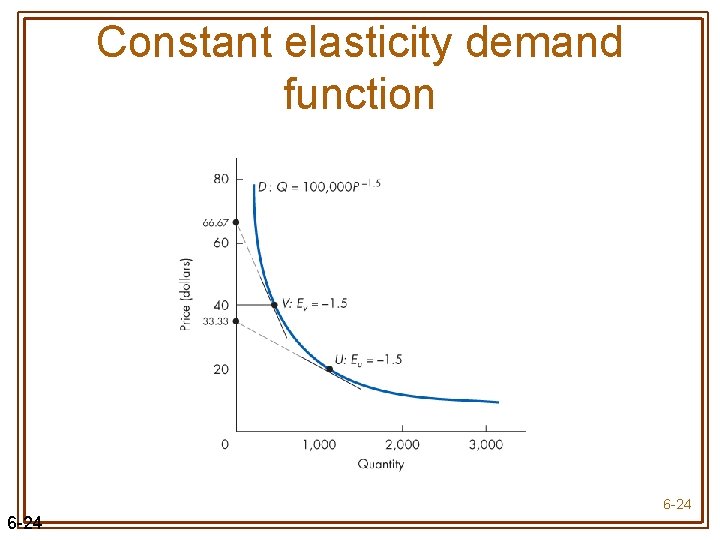
Elasticity (Generally) Varies Along a Demand Curve • For linear demand, price and E vary directly • The higher the price, the more elastic is demand • The lower the price, the less elastic is demand • For curvilinear demand, no general rule about the relation between price and quantity • Special case of Q = a. Pb which has a constant price elasticity (equal to b) for all prices 6 -21

Constant elasticity demand function 6 -22

Constant Elasticity of Demand (Figure 6. 3) 6 -23

Constant elasticity demand function 6 -24

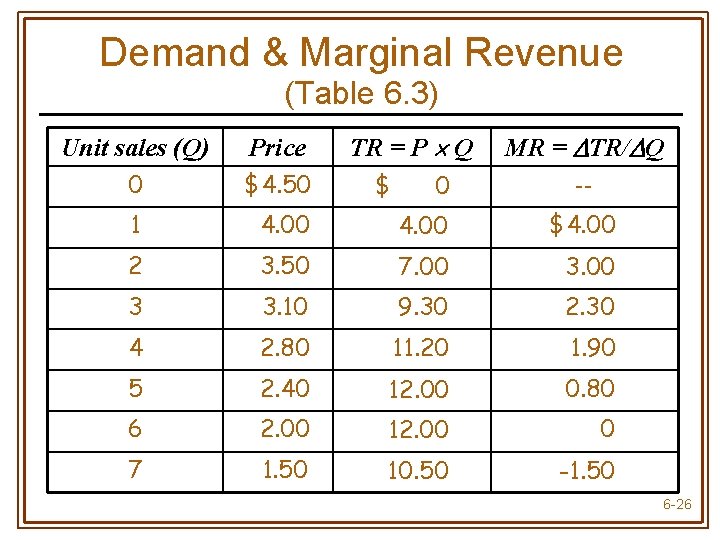
Marginal Revenue • Marginal revenue (MR) is the change in total revenue per unit change in output • Since MR measures the rate of change in total revenue as quantity changes, MR is the slope of the total revenue (TR) curve 6 -25

Demand & Marginal Revenue (Table 6. 3) TR = P Q MR = TR/ Q Unit sales (Q) Price 0 $4. 50 1 4. 00 $4. 00 2 3. 50 $7. 00 $3. 00 3 3. 10 $9. 30 $2. 30 4 2. 80 $11. 20 $1. 90 5 2. 40 $12. 00 $0. 80 6 2. 00 $12. 00 $0 7 1. 50 $10. 50 $-1. 50 $ 0 -- 6 -26

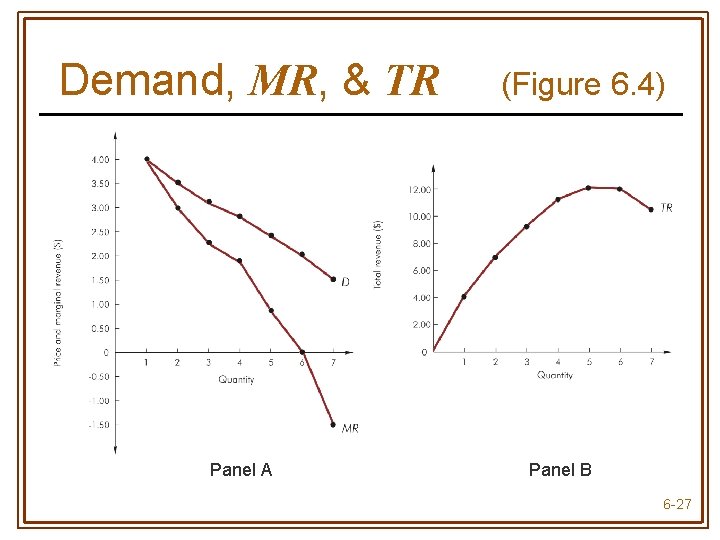
Demand, MR, & TR Panel A (Figure 6. 4) Panel B 6 -27

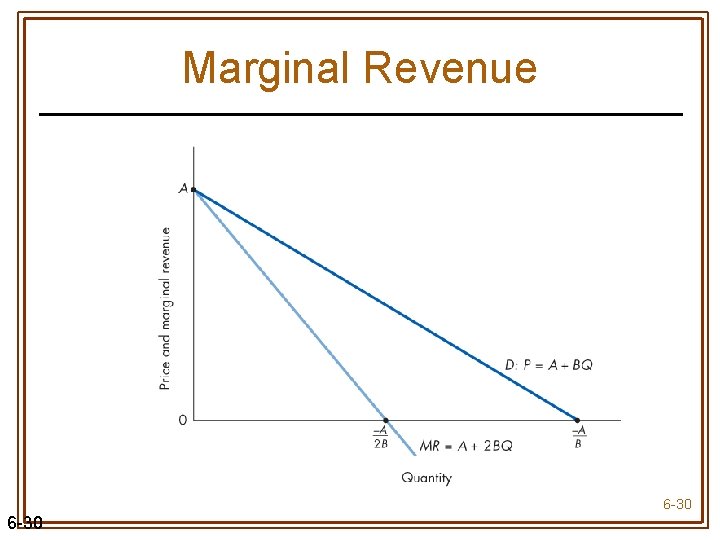
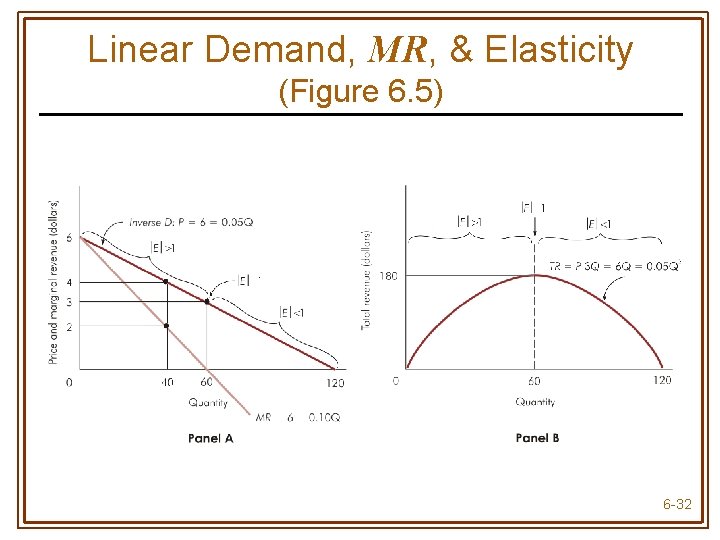
Demand & Marginal Revenue • When inverse demand is linear, P = A + BQ (A > 0, B < 0) • Marginal revenue is also linear, intersects the vertical (price) axis at the same point as demand, & is twice as steep as demand MR = A + 2 BQ 6 -28

Proof 6 -29

Marginal Revenue 6 -30

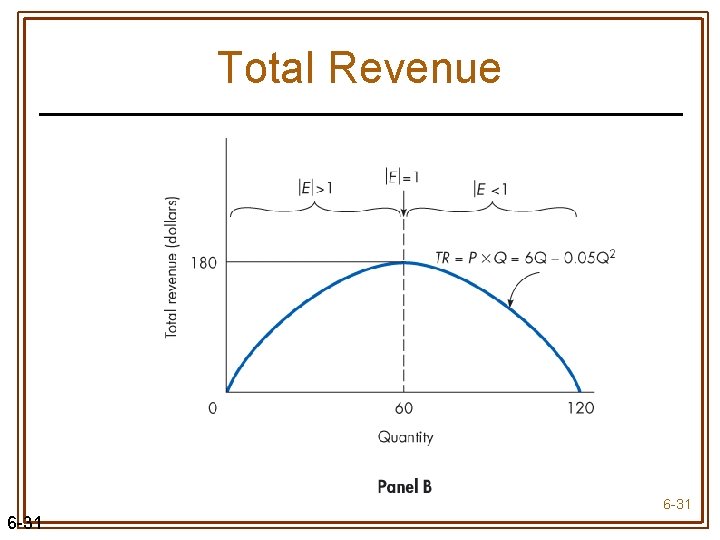
Total Revenue 6 -31

Linear Demand, MR, & Elasticity (Figure 6. 5) 6 -32

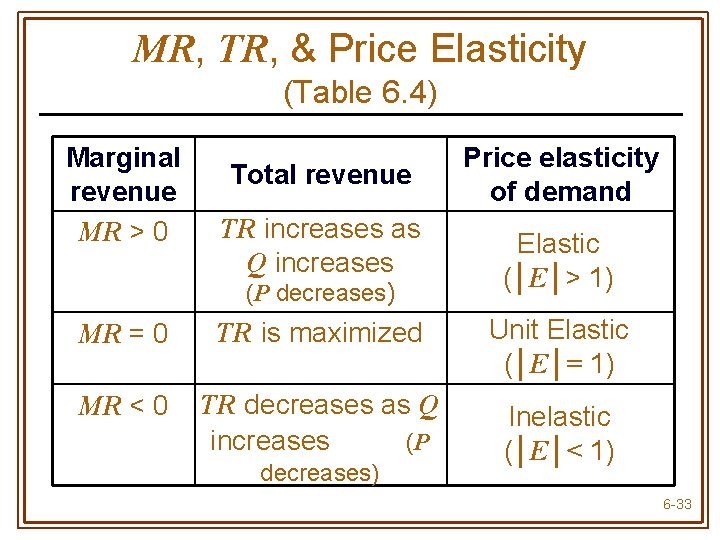
MR, TR, & Price Elasticity (Table 6. 4) Marginal revenue MR > 0 Total revenue TR increases as Q increases (P decreases) Price elasticity of demand Elastic (│E│> 1) MR = 0 TR is maximized Unit Elastic (│E│= 1) MR < 0 TR decreases as Q increases (P Inelastic (│E│< 1) decreases) 6 -33

Marginal Revenue & Price Elasticity • For all demand & marginal revenue curves, the relation between marginal revenue, price, & elasticity can be expressed as 6 -34

Proof 6 -35

Marginal Revenue & Price Elasticity Note that as E - that MR P 6 -36

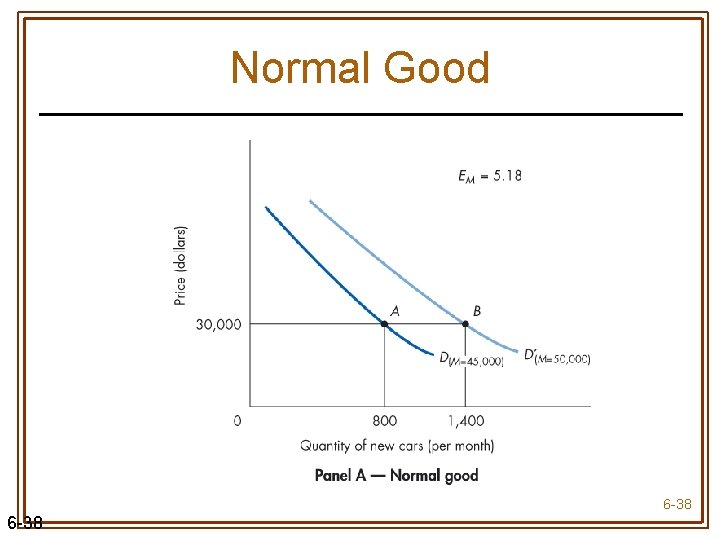
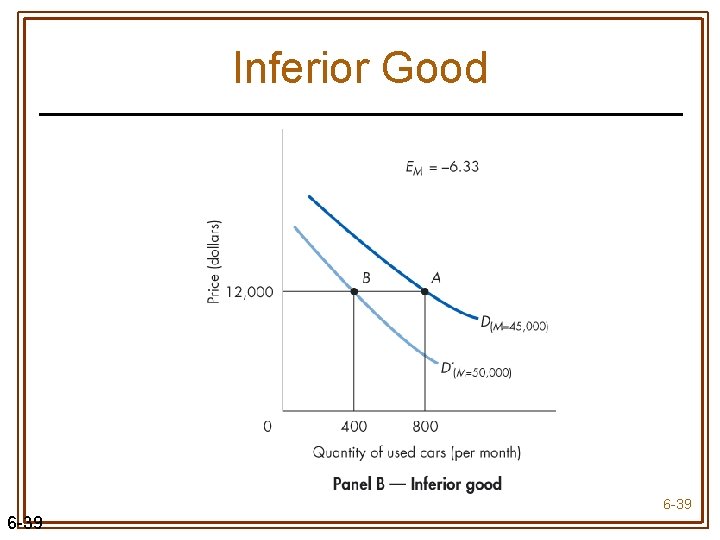
Income Elasticity • Income elasticity (EM) measures the responsiveness of quantity demanded to changes in income, holding the price of the good & all other demand determinants constant • Positive for a normal good • Negative for an inferior good 6 -37

Normal Good 6 -38

Inferior Good 6 -39

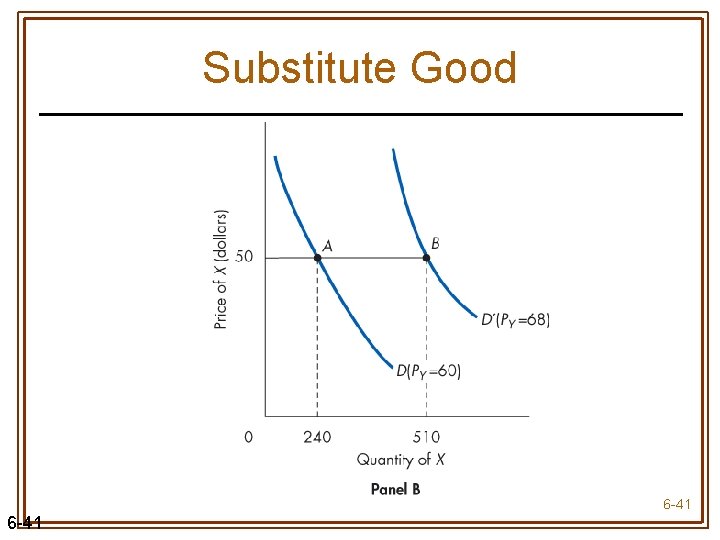
Cross-Price Elasticity • Cross-price elasticity (EXR) measures the responsiveness of quantity demanded of good X to changes in the price of related good R, holding the price of good X & all other demand determinants for good X constant • Positive when the two goods are substitutes • Negative when the two goods are complements 6 -40

Substitute Good 6 -41

Interval Elasticity Measures • To calculate interval measures of income & cross-price elasticities, the following formulas can be employed 6 -42

Point Elasticity Measures • For the linear demand function Q = a + b. P + c. M + d. PR, point measures of income & cross-price elasticities can be calculated as 6 -43

6 -44

6 -45