Chapter 6 Concurrency Control on Objects Notions of

Chapter 6: Concurrency Control on Objects: Notions of Correctness • 6. 2 Histories and Schedules • 6. 3 CSR for Flat Object Transactions • 6. 4 Tree Reducibility • 6. 5 Sufficient Conditions for Tree Reducibility • 6. 6 Exploiting State-Based Commutativity • 6. 7 Lessons Learned „No matter how complicated a problem is, it usually can be reduced to a simple comprehensible form which is often the best solution“ (An Wang) „Every problem has a simple, easy-to-understand, wrong answer. (Anonymous) 6/11/2021 Transactional Information Systems 1

Object Model Definition 2. 3 (Object-Model Transaction): A transaction t is a (finite) tree of labeled nodes with • the transaction identifier as the label of the root node, • the names and parameters of invoked operations as labels of inner nodes, and • page-model read/write operations as labels of leaf nodes, along with a partial order < on the leaf nodes such that for all leaf-node operations p and q with p of the form w(x) and q of the form r(x) or w(x) or vice versa, we have p<q q<p Special case: layered transactions (all leaves have same distance from root) Derived inner-node ordering: a < b if all leaf-node descendants of a precede all leaf-node descendants of b 6/11/2021 Transactional Information Systems 2

Example: DBS Internal Layers t 1 Search („Austin“) Fetch(x) Fetch(y) Store(z) r (r) r (p) r (q) r (f) 6/11/2021 r (l) r (p) Transactional Information Systems w (p) r (r) r (l) w (l) 3

Example: Business Objects t 2 Withdraw (x, 1000) Deposit (y, 1000) Append (h, . . . ) ^ ^ Fetch (a) Fetch (d) Store (e) Modify (d) Modify (a) Search (. . . ) Fetch (x) Modify (x) r (r) r (l) r (p) 6/11/2021 r (p) w (p) r (s) r (t) w (t) r (s)w (s) Transactional Information Systems ^ ^ Search (. . . ) Fetch (y) Modify (y) r (r) r (l) r (q) w (q) 4

Object-Model Schedules Definition 6. 1 (Object-model history): For transaction trees {t 1, . . . , tn} a history s is a partially ordered forest (op(s), <s) with node set op(s) and partial order <s of leaves such that • op(s) i=1. . n opi i=1. . n {ci, ai} and i=1. . n opi op(s) • for all ti: ci op(s) ai op(s) • ai or ci is a leaf node with ti as parent • i=1. . n <i <s • for all ti and for all p opi: p <s ai or p <s ci • for all leaves p, q that access the same data item with p or q being a write: either p <s q or q <s p Definition 6. 2 (Tree-consistent node ordering): In history s = (op(s), <s) the leaf ordering <s is extended to arbitrary nodes: p <s q if for all leaf-level descendants p‘ of p and q‘ of q: p‘ <s q‘. Definition 6. 3 (Object-model schedule): A prefix of history s = (op(s), <s) is a forest s‘ (op(s‘), <s‘) with op(s‘) op(s) and <s‘ <s s. t. for each p op(s‘) all ancestors of p and all nodes q with q <s p are in op(s‘) and <s‘ equals <s when restricted to op(s‘). An object-model schedule is a prefix of an object-model history. 6/11/2021 Transactional Information Systems 5

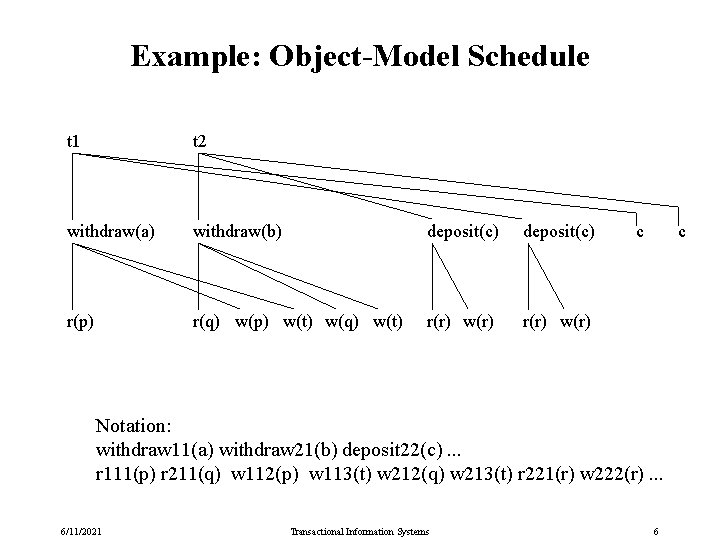
Example: Object-Model Schedule t 1 t 2 withdraw(a) withdraw(b) deposit(c) r(p) r(q) w(p) w(t) w(q) w(t) r(r) w(r) c c Notation: withdraw 11(a) withdraw 21(b) deposit 22(c). . . r 111(p) r 211(q) w 112(p) w 113(t) w 212(q) w 213(t) r 221(r) w 222(r). . . 6/11/2021 Transactional Information Systems 6

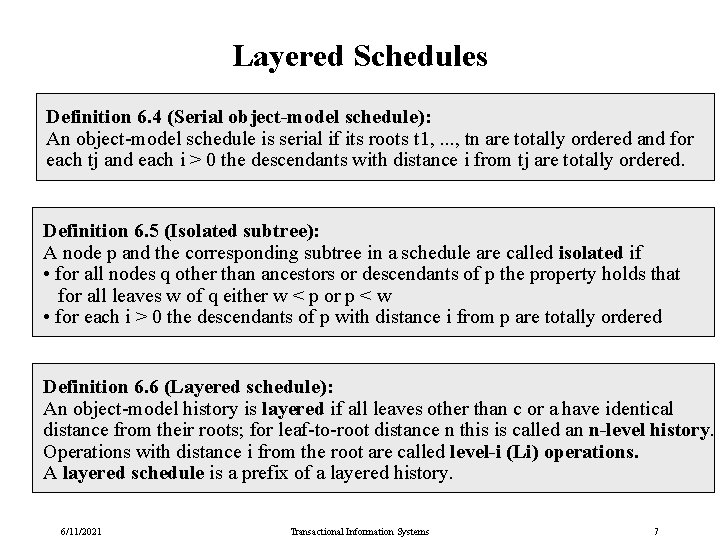
Layered Schedules Definition 6. 4 (Serial object-model schedule): An object-model schedule is serial if its roots t 1, . . . , tn are totally ordered and for each tj and each i > 0 the descendants with distance i from tj are totally ordered. Definition 6. 5 (Isolated subtree): A node p and the corresponding subtree in a schedule are called isolated if • for all nodes q other than ancestors or descendants of p the property holds that for all leaves w of q either w < p or p < w • for each i > 0 the descendants of p with distance i from p are totally ordered Definition 6. 6 (Layered schedule): An object-model history is layered if all leaves other than c or a have identical distance from their roots; for leaf-to-root distance n this is called an n-level history. Operations with distance i from the root are called level-i (Li) operations. A layered schedule is a prefix of a layered history. 6/11/2021 Transactional Information Systems 7

Examples of Non-layered Schedules 6/11/2021 t 2 withdraw(a) withdraw(b) r(p) r(q) w(p) w(t) t 1 t 2 deposit(c) w(q) w(t) r(r) w(r) withdraw(a) withdraw(b) r(p) r(q) w(p) w(t) w(q) w(t) r(r) w(r) Transactional Information Systems 8

Chapter 6: Concurrency Control on Objects: Notions of Correctness • 6. 2 Histories and Schedules • 6. 3 CSR for Flat Object Transactions • 6. 4 Tree Reducibility • 6. 5 Sufficient Conditions for Tree Reducibility • 6. 6 Exploiting State-Based Commutativity • 6. 7 Lessons Learned 6/11/2021 Transactional Information Systems 9

Flat Object Schedules Definition 6. 7 (Flat object schedule): A 2 -level schedule s is called flat if for each p, q of L 1 operations: • for all p‘ child(p) and all q‘ child(q): p‘ <s q‘ or for all p‘ child(p) and all q‘ child(q): q‘ <s p‘, and • for all p‘, p‘‘ child(p): p‘ <s p‘‘ or p‘‘ <s p‘ Definition 6. 8 ((State-independent) Commutative operations): Operations p and q are commutative if for all possible sequences of operations and the return parameters in the sequence p q are identical to those in q p . 6/11/2021 Transactional Information Systems 10

Example: Flat Object Schedule t 1 t 2 withdraw(a) withdraw(b) r(p) w(t) r(q) w(t) (State-independent) Commutativity table: withdraw (x, 1) deposit (x, 1) getbalance (x) 6/11/2021 deposit(c) r(r) w(r) withdraw (x, 2) deposit (x, 2) getbalance (x) _ _ _ Transactional Information Systems _ + _ _ _ + 11

Commutativity-based Reducibility Definition 6. 9 (Commutativity-based Reducibility): A flat object schedule s is commutativity-based reducible if it can be transformed into a serial schedule by apply the following rules: • Commutativity rule: the order of ordered operations p, q, say p <s q, can be reversed if • both are isolated, adjacent, and commutative and • the operations belong to different transactions. • Ordering rule: Unordered leaf operations p, q can be arbitrarily ordered if they are commutative. Definition 6. 10 (Conflict equivalence and conflict serializability): Two flat object schedules s and s‘ are conflict equivalent if they consist of the same operations and have the same ordering for all non-commutative pairs of L 1 operations. s is conflict serializable if it is conflict equivalent to a serial schedule. Theorem 6. 11: For a flat object schedule s the following three conditions are equivalent: s is conflict serializable, s has an acyclic conflict graph, s is commutativity-based reducible. 6/11/2021 Transactional Information Systems 12

Chapter 6: Concurrency Control on Objects: Notions of Correctness • 6. 2 Histories and Schedules • 6. 3 CSR for Flat Object Transactions • 6. 4 Tree Reducibility • 6. 5 Sufficient Conditions for Tree Reducibility • 6. 6 Exploiting State-Based Commutativity • 6. 7 Lessons Learned 6/11/2021 Transactional Information Systems 13

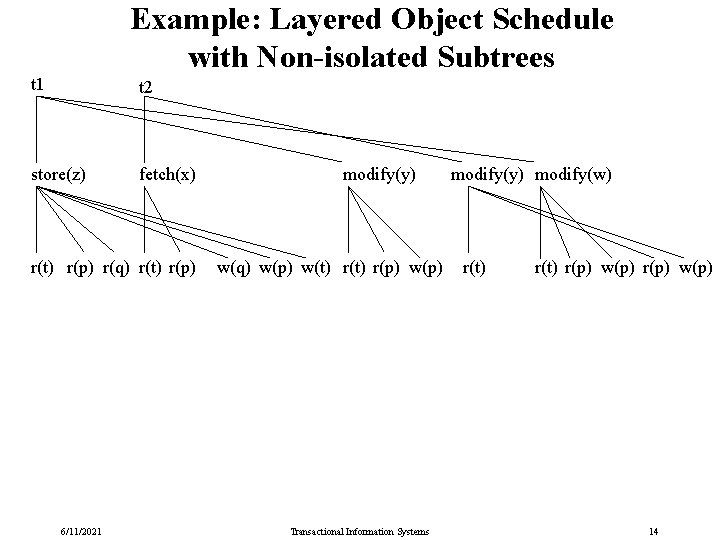
Example: Layered Object Schedule with Non-isolated Subtrees t 1 t 2 store(z) fetch(x) r(t) r(p) r(q) r(t) r(p) 6/11/2021 modify(y) w(q) w(p) w(t) r(p) w(p) Transactional Information Systems modify(y) modify(w) r(t) r(p) w(p) 14

Tree Reducibility Definition 6. 12 (Tree reducibility): Object-model history s = (op(s), <s) is tree reducible if it can be transformed into a total order of its roots by apply the following rules: • Commutativity rule: the order of ordered leaf operations p, q, say p <s q, can be reversed if • both are isolated, adjacent, and commutative, and • the operations belong to different transactions, and • p and q do not have ancestors, p‘ and q‘, that are non-commutative and totally ordered in the order p‘ <s q‘. • Ordering rule: Unordered leaf operations p, q can be arbitrarily ordered if they are commutative. • Tree pruning rule: An isolated subtree can be replaced by its root. An object-model schedule is tree reducible if its committed projection is tree reducible. 6/11/2021 Transactional Information Systems 15

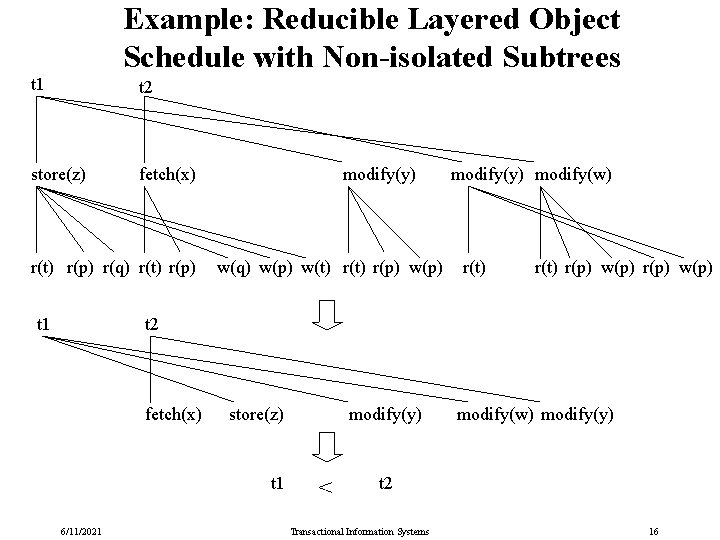
Example: Reducible Layered Object Schedule with Non-isolated Subtrees t 1 t 2 store(z) fetch(x) r(t) r(p) r(q) r(t) r(p) t 1 modify(y) w(q) w(p) w(t) r(p) w(p) modify(y) modify(w) r(t) r(p) w(p) t 2 fetch(x) store(z) t 1 6/11/2021 modify(y) < modify(w) modify(y) t 2 Transactional Information Systems 16

Example: Non-reducible Layered Object Schedule t 1 t 2 store(z) fetch(x) r(t) r(p) r(q) 6/11/2021 w(q) w(p) Transactional Information Systems r(t) r(p) w(t) 17

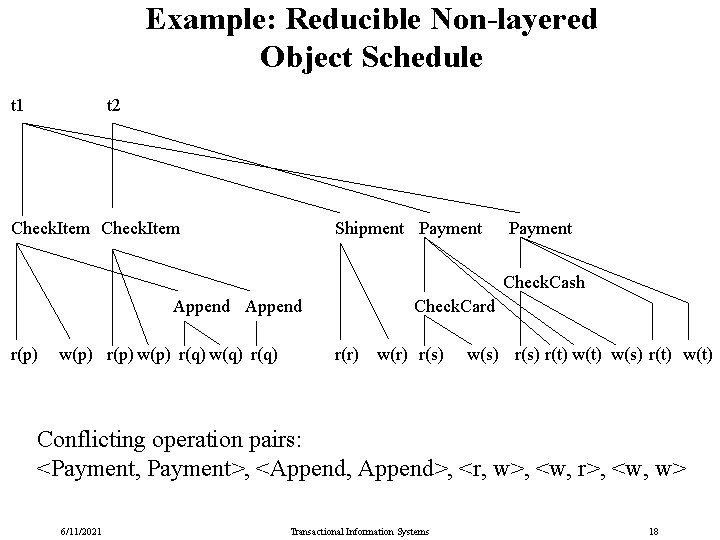
Example: Reducible Non-layered Object Schedule t 1 t 2 Check. Item Shipment Payment Check. Cash Append r(p) w(p) r(q) w(q) r(q) Check. Card r(r) w(r) r(s) w(s) r(t) w(t) Conflicting operation pairs: <Payment, Payment>, <Append, Append>, <r, w>, <w, r>, <w, w> 6/11/2021 Transactional Information Systems 18

Chapter 6: Concurrency Control on Objects: Notions of Correctness • 6. 2 Histories and Schedules • 6. 3 CSR for Flat Object Transactions • 6. 4 Tree Reducibility • 6. 5 Sufficient Conditions for Tree Reducibility • 6. 6 Exploiting State-Based Commutativity • 6. 7 Lessons Learned 6/11/2021 Transactional Information Systems 19

Sufficient Conditions for Tree Reducibility Definition 6. 13 (Level-to-level schedule): For an n-level schedule s = (op(s), <s) with layers L 0, . . . , Ln, the level-to-level schedule from Li to L(i-1), or Li-to-L(i-1) schedule, is a conventional 2 -level schedule s‘ = (op(s‘), <s‘) with • op(s‘) consisting of the L(i-1) operations of s, • <s‘ being the restriction of the extended order <s to the L(i-1) operations, • Li operations of s as roots, and • the same parent-child relationship as in s. Theorem 6. 14: Let s be an n-level schedule. If for each i, 0 < i n, the Li-to-L(i-1) schedule derived from s is in OCSR, then s is tree-reducible. Definition 6. 15 (Conflict faithfulness): A layered schedule s = (op(s), <s) is conflict-faithful if for each pair p, q op(s) s. t. p, q are non-commutative and for each i>0 there is at least one operation pair p‘, q‘ s. t. p‘ and q‘ are descendants of p and q with distance i and are in conflict. Theorem 6. 16: Let s be an n-level schedule. If s is conflict-faithful and for each i, 0 < i n, the Li-to-L(i-1) schedule derived from s is in CSR, then s is tree-reducible. 6/11/2021 Transactional Information Systems 20

Proof Sketch for Theorem 6. 14 Consider adjacent levels Li, L(i-1): • CSR of the Li-to-L(i-1) schedules allows isolating the Li ops • Conflicting Li ops f, g are not reordered: • Because of the Li conflict and the L(i+1)-to-Li schedule being CSR, f and g must be ordered • Because of the Li-to-L(i-1) schedule being OCSR this order is not reversed by the Li-to-L(i-1) serialization 6/11/2021 Transactional Information Systems induction on i 21

Proof Sketch for Theorem 6. 16 Consider adjacent levels Li, L(i-1): • CSR of the Li-to-L(i-1) schedules allows isolating the Li ops • Conflicting Li ops f, g are not reordered: • Because of the Li conflict and the L(i+1)-to-Li schedule being CSR, f and g must be ordered, say f < g • Because of conflict-faithfulness f must and g must have conflicting children f‘, g‘ with f‘ < g‘ • CSR cannot reverse the order of f‘ and g‘, so the Li-to-L(i-1) serialization must be compatible with the Li order f < g 6/11/2021 Transactional Information Systems induction on i 22

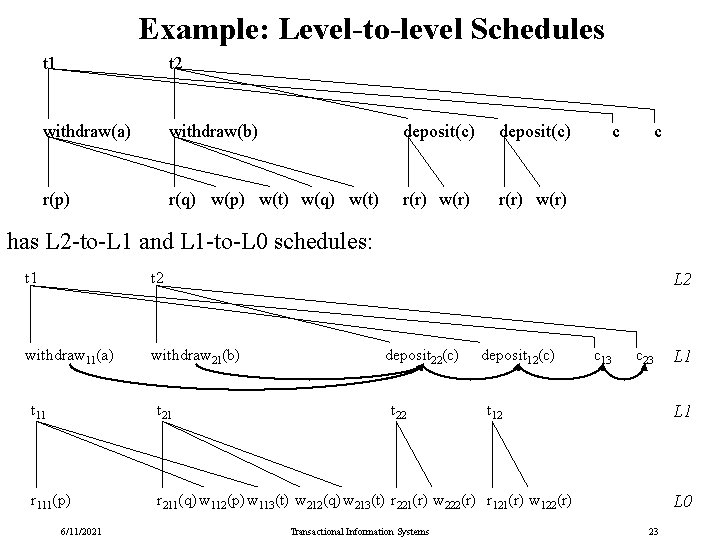
Example: Level-to-level Schedules t 1 t 2 withdraw(a) withdraw(b) deposit(c) r(p) r(q) w(p) w(t) w(q) w(t) r(r) w(r) c c has L 2 -to-L 1 and L 1 -to-L 0 schedules: t 1 t 2 withdraw 11(a) withdraw 21(b) L 2 deposit 22(c) t 11 t 21 r 111(p) r 211(q) w 112(p) w 113(t) w 212(q) w 213(t) r 221(r) w 222(r) r 121(r) w 122(r) 6/11/2021 t 22 deposit 12(c) Transactional Information Systems c 13 c 23 t 12 L 1 L 0 23

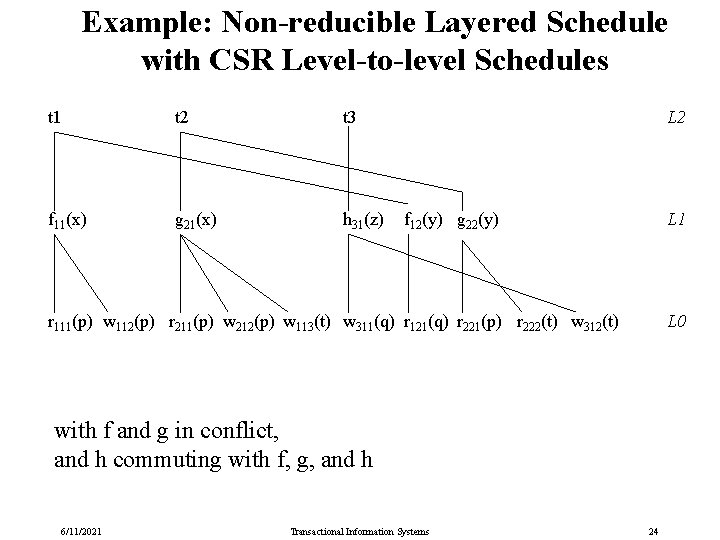
Example: Non-reducible Layered Schedule with CSR Level-to-level Schedules t 1 t 2 t 3 f 11(x) g 21(x) h 31(z) L 2 f 12(y) g 22(y) L 1 r 111(p) w 112(p) r 211(p) w 212(p) w 113(t) w 311(q) r 121(q) r 221(p) r 222(t) w 312(t) L 0 with f and g in conflict, and h commuting with f, g, and h 6/11/2021 Transactional Information Systems 24

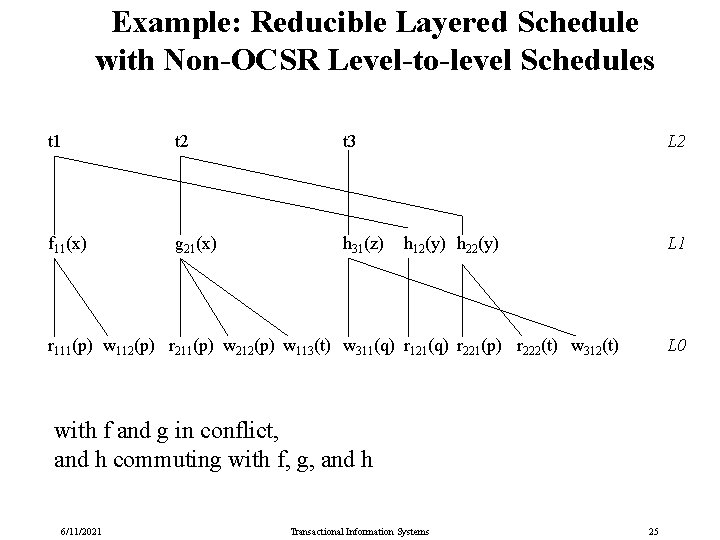
Example: Reducible Layered Schedule with Non-OCSR Level-to-level Schedules t 1 t 2 t 3 f 11(x) g 21(x) h 31(z) L 2 h 12(y) h 22(y) L 1 r 111(p) w 112(p) r 211(p) w 212(p) w 113(t) w 311(q) r 121(q) r 221(p) r 222(t) w 312(t) L 0 with f and g in conflict, and h commuting with f, g, and h 6/11/2021 Transactional Information Systems 25

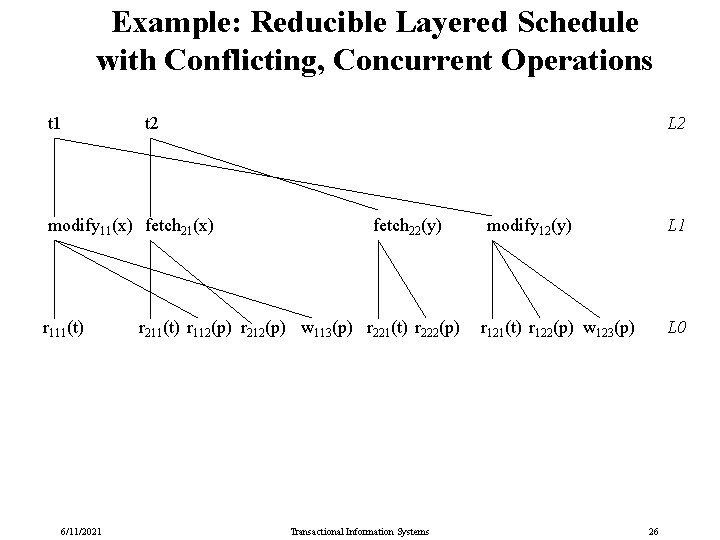
Example: Reducible Layered Schedule with Conflicting, Concurrent Operations t 1 t 2 modify 11(x) fetch 21(x) r 111(t) 6/11/2021 L 2 fetch 22(y) r 211(t) r 112(p) r 212(p) w 113(p) r 221(t) r 222(p) Transactional Information Systems modify 12(y) L 1 r 121(t) r 122(p) w 123(p) L 0 26

Chapter 6: Concurrency Control on Objects: Notions of Correctness • 6. 2 Histories and Schedules • 6. 3 CSR for Flat Object Transactions • 6. 4 Tree Reducibility • 6. 5 Sufficient Conditions for Tree Reducibility • 6. 6 Exploiting State-Based Commutativity • 6. 7 Lessons Learned 6/11/2021 Transactional Information Systems 27

State-dependent Commutativity Definition 6. 17 (State-dependent commutativity): Operations p and q on the same object are commutative in object state if for all operation sequences the return parameters in the sequence pq applied to are identical to those in qp applied to . Example: • : x. balance = 40 s: withdraw 1(x, 30) deposit 2(x, 50) deposit 2(y, 50) withdraw 1(y, 30) would allow commuting the first step with both steps of t 2 • : x. balance = 20 s: withdraw 1(x, 30) deposit 2(x, 50) deposit 2(y, 50) withdraw 1(y, 30) would not allow commuting the first two steps 6/11/2021 Transactional Information Systems 28

Return-value Commutativity Definition 6. 18 (Return-value commutativity): An operation execution p ( x 1, . . . , xm, y 1, . . . , yn) is return-value commutative with an immediately following operation execution q ( x 1‘, . . . , xm‘‘, y 1‘, . . . , yn‘‘) if for every possible sequences and s. t. p and q have indeed yielded the given return values in pq , all operations in the sequence qp yield identical return values. Example: • : x. balance = 40 s: withdraw 1(x, 30) ok deposit 2(x, 50) ok. . . withdraw ok is return-value commutative with deposit • : x. balance = 20 s: withdraw 1(x, 30) no deposit 2(x, 50) ok. . . withdraw no is not return-value commutative with deposit 6/11/2021 Transactional Information Systems 29

Examples: Return-value Commutativity Tables bank accounts (counters): queues: p q withdraw (x, 1) ok withdraw (x, 1) no deposit (x, 1) ok p q + _ + + enq ok enq one deq ok deq empty enq ok _ impossible enq one _ impossible deq ok + _ deq empty 6/11/2021 withdraw deposit (x, 2) ok (x, 2) no (x, 2) ok _ + + Transactional Information Systems _ + _ _ _ impossible _ + 30

Example: Schedule on Counter Objects t 1 equivalent to serial order t 1 < t 2 decr(x, 20) no incr(x, 30) ok r(p) x=15 y=45 r(p) w(p) x=15 y=45 decr(y, 20) ok incr(y, 30) no r(p) w(p) x=45 y=45 r(p) x=15 y=25 with constraints 0 x 50, 0 y 50 6/11/2021 Transactional Information Systems 31

Chapter 6: Concurrency Control on Objects: Notions of Correctness • 6. 2 Histories and Schedules • 6. 3 CSR for Flat Object Transactions • 6. 4 Tree Reducibility • 6. 5 Sufficient Conditions for Tree Reducibility • 6. 6 Exploiting State-Based Commutativity • 6. 7 Lessons Learned 6/11/2021 Transactional Information Systems 32

Lessons Learned • Commutativity and abstraction arguments lead to the fundamental criterion of tree reducibility • For layered schedules, CSR can be iterated from level to level • Compared to page-model CSR, concurrency can be improved, potentially by orders of magnitude • State-based commutativity can further enhance concurrency, but is more complex to manage 6/11/2021 Transactional Information Systems 33