Chapter 6 Bandpass Random Processes Bandpass Random Processes

Chapter 6 Bandpass Random Processes Ø Ø Bandpass Random Processes PSD of bandpass random processes BP Filtered White Noise Sinusoids in Gaussian Noise Huseyin Bilgekul EEE 461 Communication Systems II Department of Electrical and Electronic Engineering Eastern Mediterranean University EEE 461 1

Homework Assignments • Return date: December 13, 2005. • Assignments: Problem 6 -38 Problem 6 -41 Problem 6 -45 Problem 6 -48 Problem 6 -50 EEE 461 2
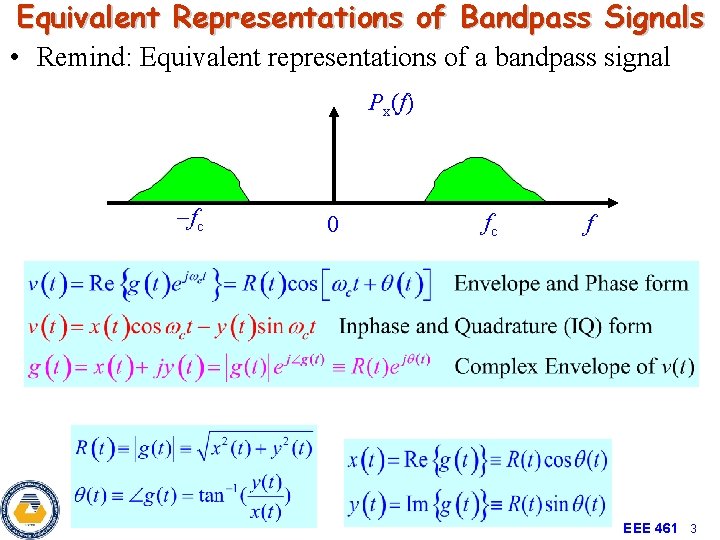
Equivalent Representations of Bandpass Signals • Remind: Equivalent representations of a bandpass signal Px(f) -fc 0 fc f EEE 461 3

Bandpass Random Process • If x(t) and y(t) are jointly WSS processes, the real bandpass process Will be WSS stationary if and only if: • If v(t) is a Gaussian random process then g(t), x(t) and y(t) are Gaussian processes since they are linear functions v(t). However R(t) θ(t) are NOT Gaussian because they are NONLIEAR functions of v(t). EEE 461 4
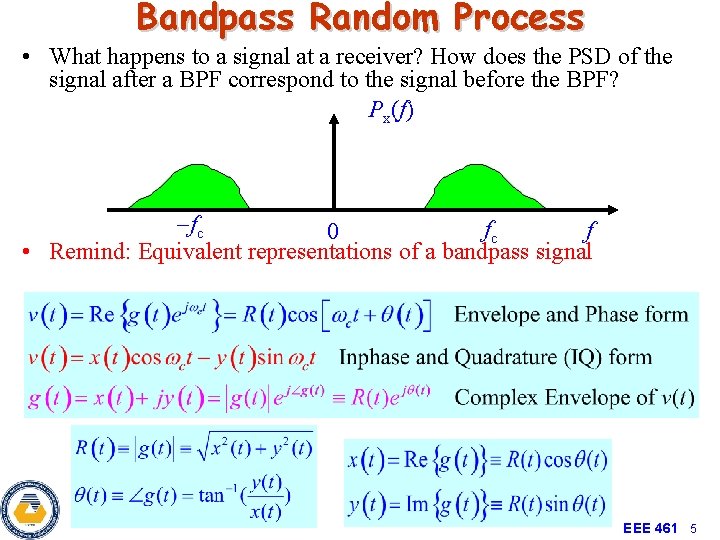
Bandpass Random Process • What happens to a signal at a receiver? How does the PSD of the signal after a BPF correspond to the signal before the BPF? Px(f) -fc fc f 0 • Remind: Equivalent representations of a bandpass signal EEE 461 5
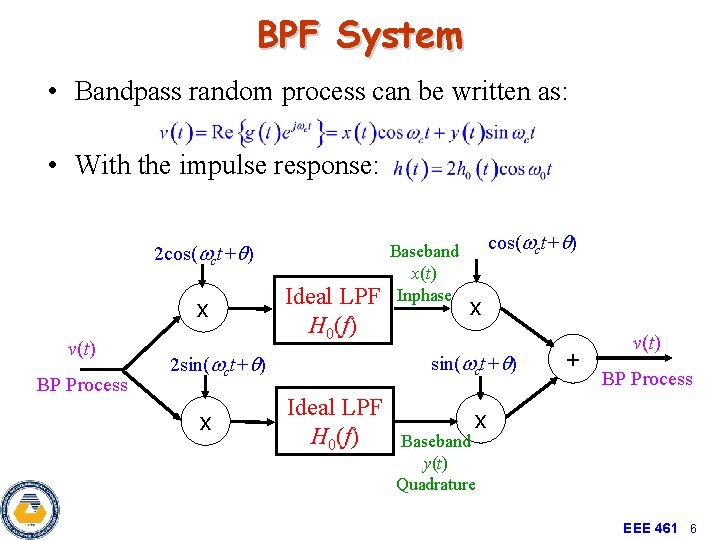
BPF System • Bandpass random process can be written as: • With the impulse response: 2 cos(wct+q) x v(t) BP Process Ideal LPF H 0(f) cos(wct+q) x sin(wct+q) 2 sin(wct+q) x Baseband x(t) Inphase Ideal LPF H 0(f) + v(t) BP Process x Baseband y(t) Quadrature EEE 461 6
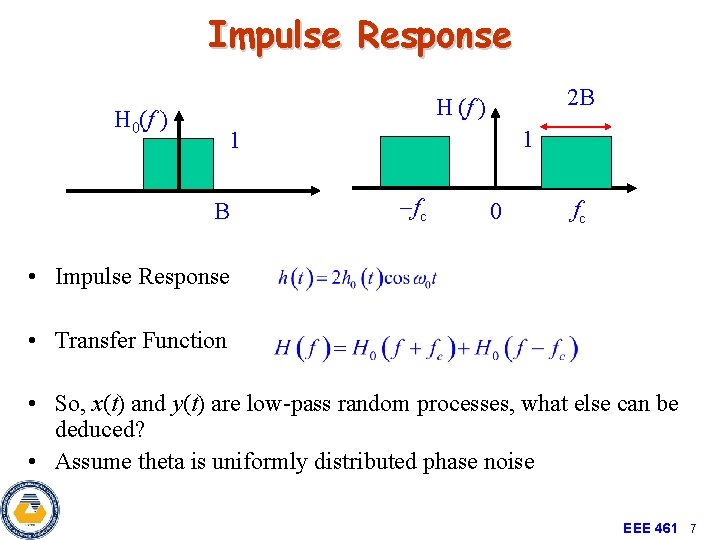
Impulse Response 2 B H (f ) H 0(f ) 1 1 B -fc 0 fc • Impulse Response • Transfer Function • So, x(t) and y(t) are low-pass random processes, what else can be deduced? • Assume theta is uniformly distributed phase noise EEE 461 7

PSD of BP Random Processes • PSD of x(t) and y(t) Pv(f ) -fc Pv(f+fc) fc Pv(f-fc) LPF -2 fc f 2 fc 0 f Px(f) or Py(f) -2 fc 0 2 fc f EEE 461 8
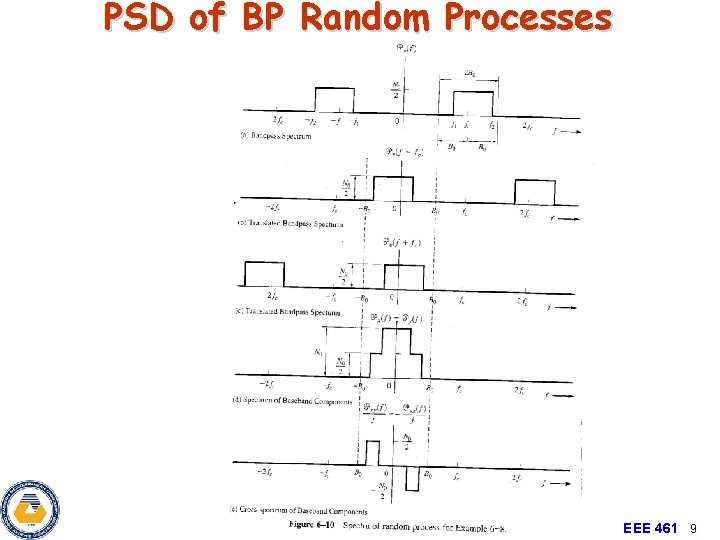
PSD of BP Random Processes EEE 461 9
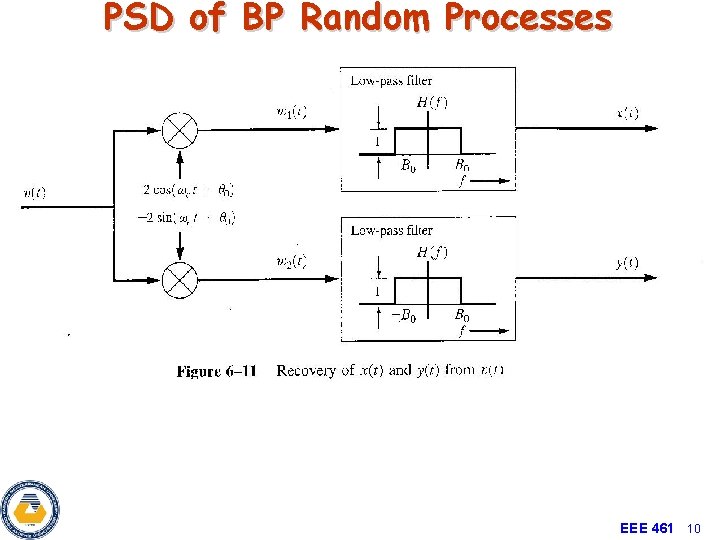
PSD of BP Random Processes EEE 461 10

Properties of WSS BP Processes • If the narrowband noise is Gaussian, then the in-phase x(t) and quadrature y(t) components are jointly Gaussian • If the narrow band noise is wide-sense stationary (WSS), then the in-phase and quadrature components are jointly WSS. • In-phase and quadrature components have the same PSD. • In-phase and quadrature components of narrowband noise are zero-mean – Noise comes original signal being passed through a narrowband linear filter • Variance of the processes is the same (area under PSD same) EEE 461 11

Properties of WSS BP Processes Continued • Bandpass PSD from baseband PSD. • PSD of I and Q from bandpass PSD EEE 461 12

BP White Noise Process • The PSD of a BP white noise process is No/2. What is the PSD and variance of the in-phase and quadrature components? • From the SNR calculations, it is clear that the variance of the white noise is: EEE 461 13

Sinusoids in Gaussian Noise • Signal is a sinusoid mixed with narrow-band additive white Gaussian noise (AWGN) • Can be written in terms of ENVELOPE and PHASE terms as: EEE 461 14

Sinusoids in Gaussian Noise • In-phase and Quadrature terms of noise Gaussian with variance s 2. • Similar transformation to that used for calculating the dart board example, the joint density can be found in polar coordinates. • Marginal density of the Envelope is Rician type. • Approaches a Gaussian if A >> s EEE 461 15
- Slides: 15