Chapter 5 Using Newtons Laws Friction Circular Motion

Chapter 5: Using Newton’s Laws: Friction, Circular Motion, Drag Forces Homework 4 Due Wednesday October 7 Chap 5: Pb. 6, Pb. 9, Pb. 25, Pb 35, Pb 42, Pb 45

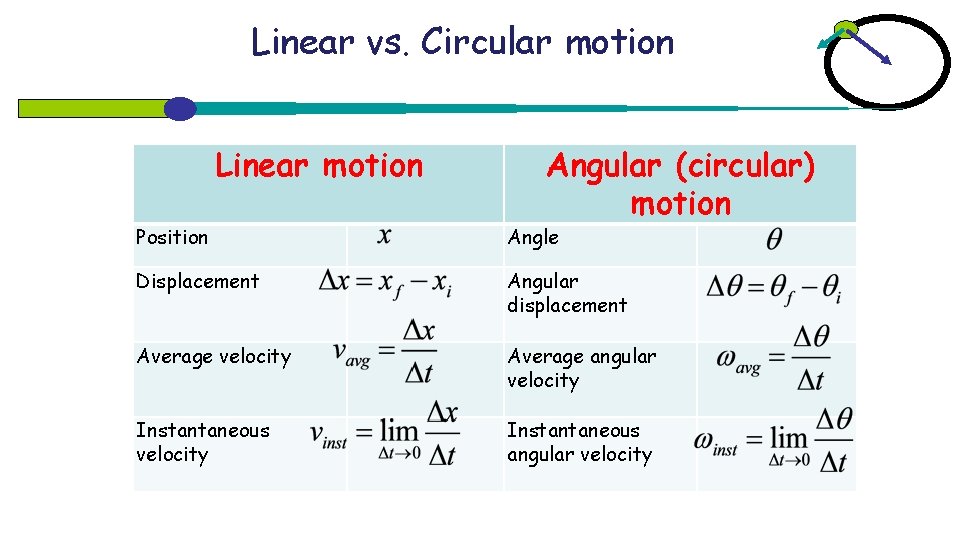
Linear vs. Circular motion Linear motion Angular (circular) motion Position Angle Displacement Angular displacement Average velocity Average angular velocity Instantaneous angular velocity

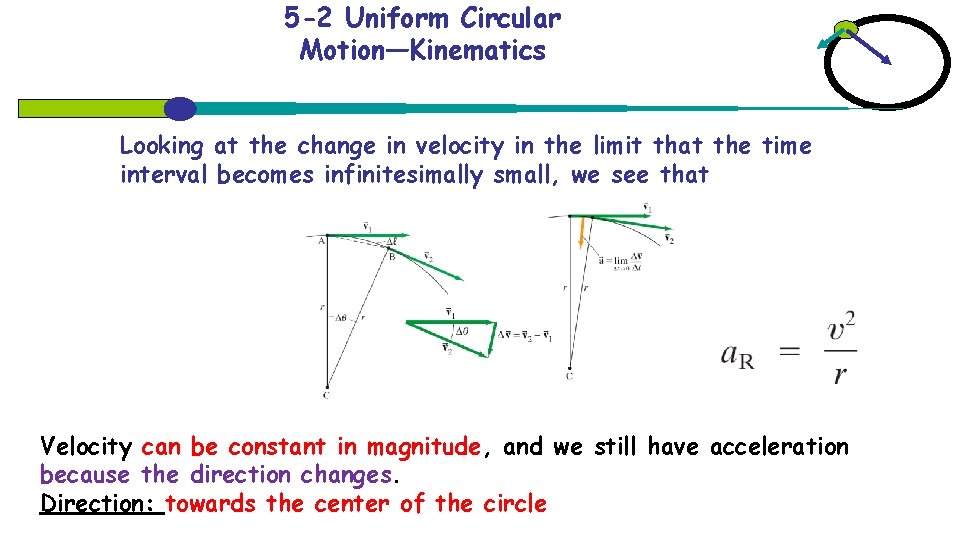
5 -2 Uniform Circular Motion—Kinematics Looking at the change in velocity in the limit that the time interval becomes infinitesimally small, we see that Velocity can be constant in magnitude, and we still have acceleration because the direction changes. Direction: towards the center of the circle

Newton’s second law • Whenever we have circular motion, we have acceleration directed towards the center of the motion. • Whenever we have circular motion, there must be a force towards the center of the circle causing the circular motion.

5 -2 Uniform Circular Motion— Kinematics This acceleration is called the centripetal, or radial, acceleration, and it points toward the center of the circle. This is due to the change of the direction of the velocity.

Uniform Circular Motion—Kinematics Example 5 -10: Ultracentrifuge. The rotor of an ultracentrifuge rotates at 50, 000 rpm (revolutions per minute). A particle at the top of a test tube is 6. 00 cm from the rotation axis. Calculate its centripetal acceleration, in “g’s. ”

Problem 57 57. (III) The position of a particle moving in the xy plane is given by where r is in meters and t is in seconds. (a) Show that this represents circular motion of radius 2. 0 m centered at the origin. (b) Determine the velocity and acceleration vectors as functions of time. (c) Determine the speed and magnitude of the acceleration. (d) Show that a= v 2/r (e) Show that the acceleration vector always points toward the center of the circle.

5 -2 Uniform Circular Motion—Kinematics Example 5 -8: Acceleration of a revolving ball. A 150 -g ball at the end of a string is revolving uniformly in a horizontal circle of radius 0. 600 m. The ball makes 2. 00 revolutions in a second. What is its centripetal acceleration?

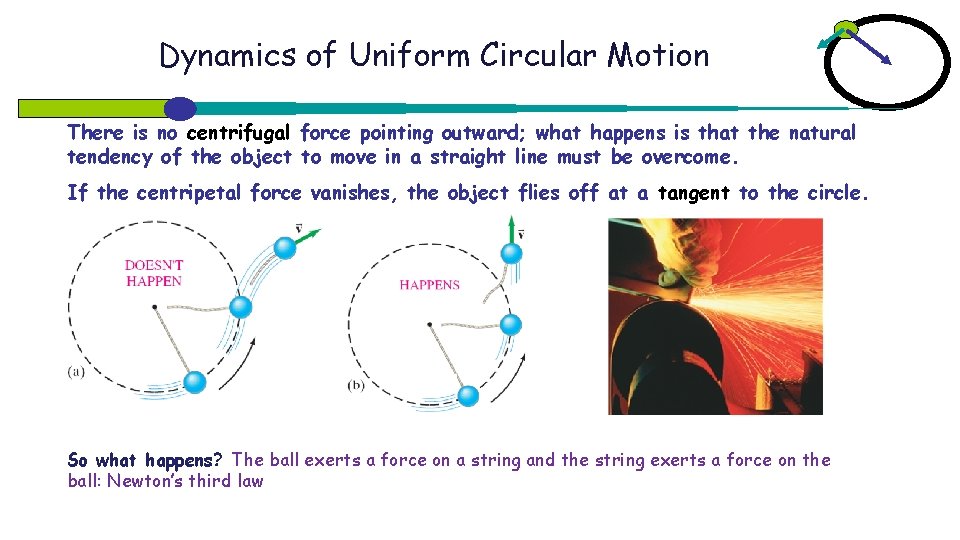
Dynamics of Uniform Circular Motion There is no centrifugal force pointing outward; what happens is that the natural tendency of the object to move in a straight line must be overcome. If the centripetal force vanishes, the object flies off at a tangent to the circle. So what happens? The ball exerts a force on a string and the string exerts a force on the ball: Newton’s third law

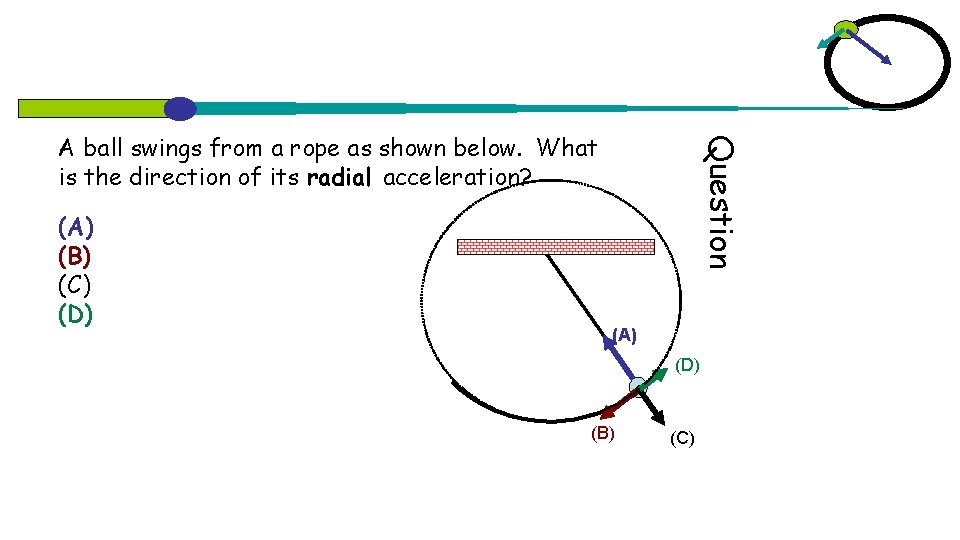
(A) (B) (C) (D) Question A ball swings from a rope as shown below. What is the direction of its radial acceleration? (A) (D) (B) (C)

Dynamics of Uniform Circular Motion Example 5 -11: Force on revolving ball (horizontal). Estimate the force a person must exert on a string attached to a 0. 150 -kg ball to make the ball revolve in a horizontal circle of radius 0. 600 m. The ball makes 2. 00 revolutions per second. Ignore the string’s mass.

Non-uniform Circular Motion If an object is moving in a circular path but at varying speeds, it must have a tangential component to its acceleration as well as the radial one.

Non-uniform Circular Motion This concept can be used for an object moving along any curved path, as any small segment of the path will be approximately circular. The total acceleration:

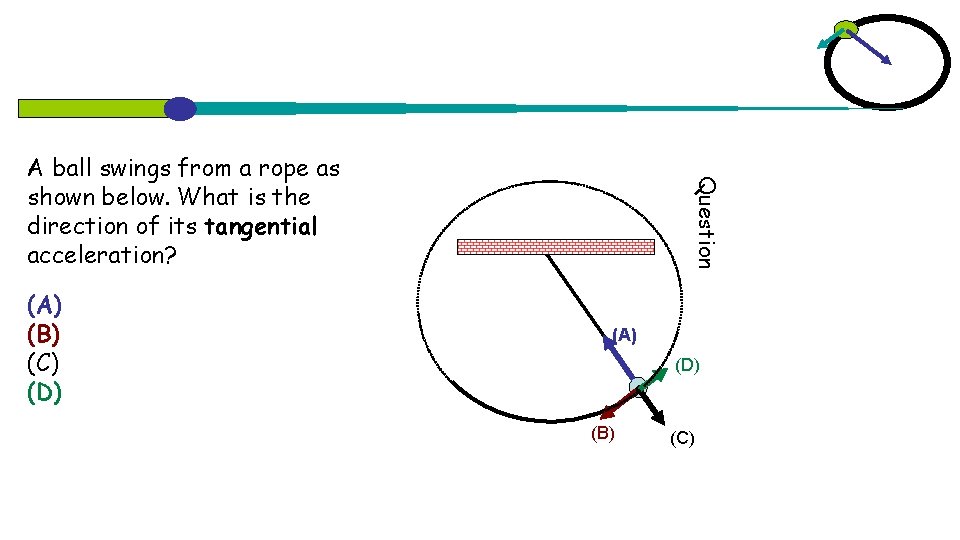
(A) (B) (C) (D) Question A ball swings from a rope as shown below. What is the direction of its tangential acceleration? (A) (D) (B) (C)

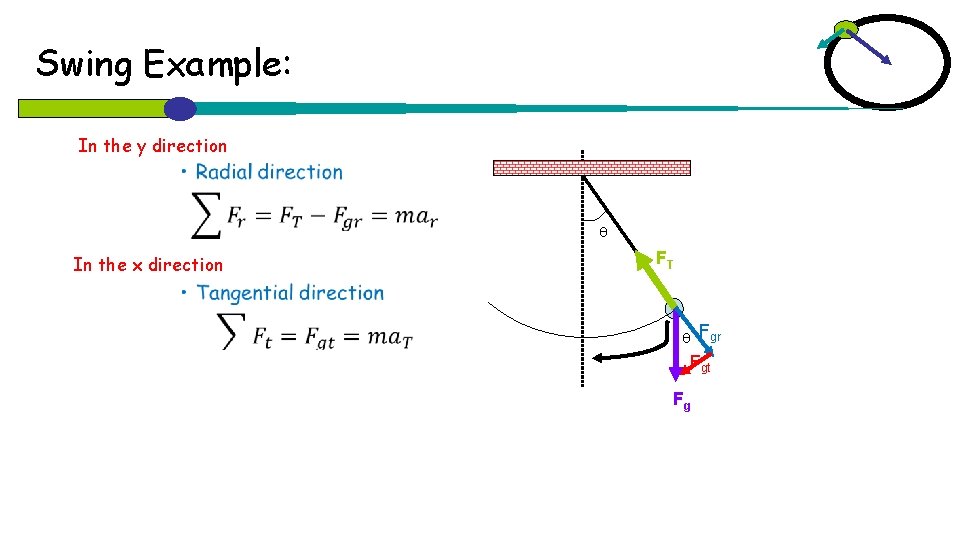
Swing Example: In the y direction • In the x direction FT Fgr Fgt Fg