Chapter 5 Trees 5 1 Binary trees n

Chapter 5 Trees 5 -1

Binary trees n A binary tree is a finite set of elements that is either empty or is partitioned into 3 disjoint subsets: root left subtree right subtree 5 -2

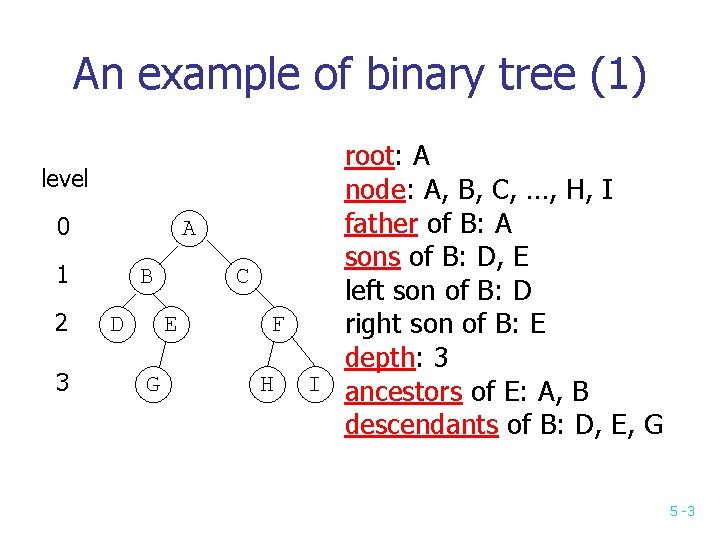
An example of binary tree (1) level 0 A 1 2 3 B D E G root: A node: A, B, C, …, H, I father of B: A sons of B: D, E C left son of B: D F right son of B: E depth: 3 H I ancestors of E: A, B descendants of B: D, E, G 5 -3

An example of binary tree (2) left descendant of B: D right descendant of B: E, G brother: B and C are brothers D and E are brothers leaf: a node that has no sons e. g. D, G, H, I left subtree of A: B right subtree of A: C D E G F H I 5 -4

Not binary trees A B D G A C E H B F D A I B (a) D E F G C E C F (b) G H I (c) 5 -5

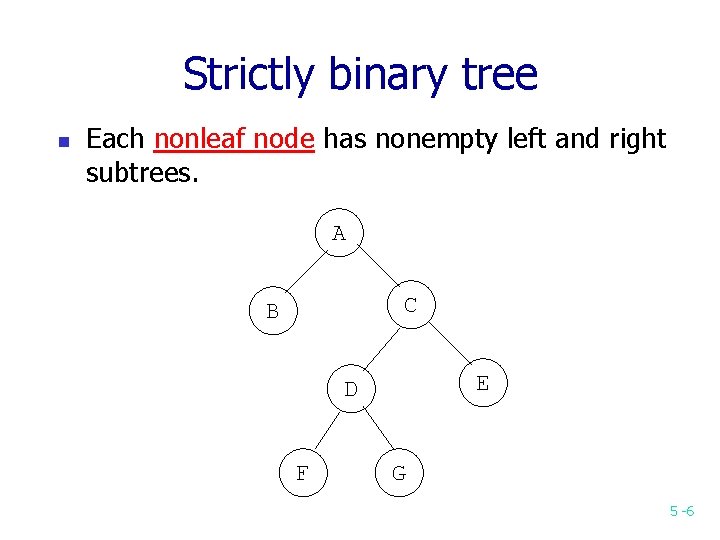
Strictly binary tree n Each nonleaf node has nonempty left and right subtrees. A C B E D F G 5 -6

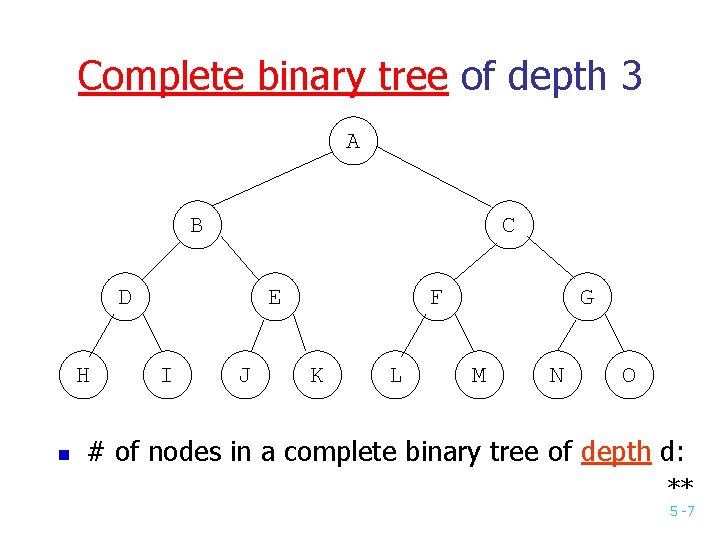
Complete binary tree of depth 3 A B C D H n E I J F K L G M N O # of nodes in a complete binary tree of depth d: ** 5 -7

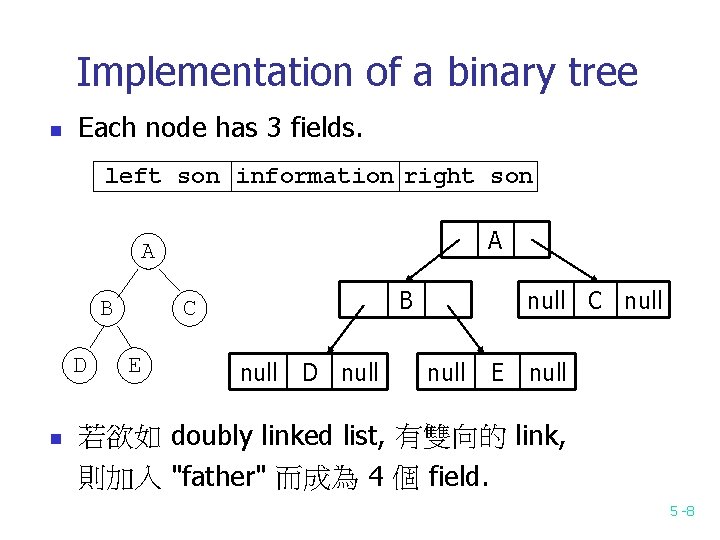
Implementation of a binary tree n Each node has 3 fields. left son information right son A A B D n B C E null D null C null E null 若欲如 doubly linked list, 有雙向的 link, 則加入 "father" 而成為 4 個 field. 5 -8

Linked array representation #define NUMNODES 500 struct nodetype{ int info; int left; int right; int father; }; struct nodetype node[NUMNODES]; 5 -9

Dynamic node representation struct nodetype{ int info; struct nodetype *left; struct nodetype *right; struct nodetype *father; }; typedef struct nodetype *NODEPTR; 5 -10

Creation of a new tree n maketree(x): Create a new tree consisting of a single node X NODEPTR maketree(int x) { NODEPTR p; p = getnode(); p->info = x; p->left = NULL; p->right = NULL; return(p); } /* end maketree */ 5 -11

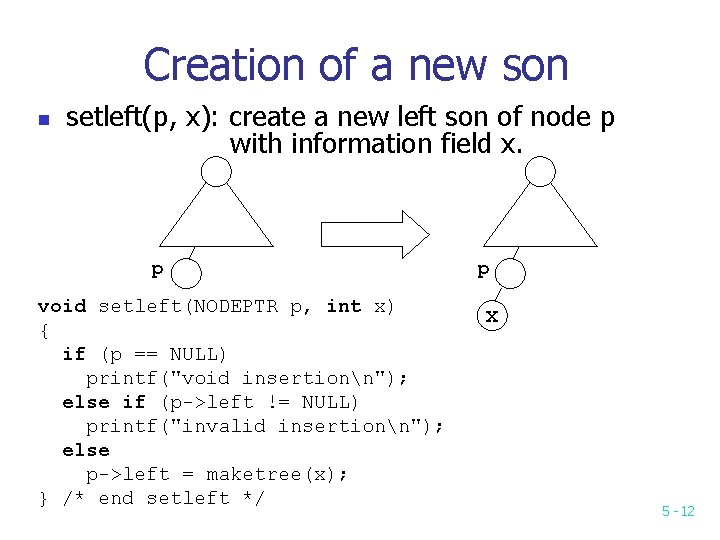
Creation of a new son n setleft(p, x): create a new left son of node p with information field x. p void setleft(NODEPTR p, int x) { if (p == NULL) printf("void insertionn"); else if (p->left != NULL) printf("invalid insertionn"); else p->left = maketree(x); } /* end setleft */ p x 5 -12

An application of binary trees n n Finding all duplicate numbers in a number series. 14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5 14 4 3 9 7 5 n n 15 18 16 20 17 build a binary search tree: smaller numbers stored in the left subtree. larger numbers stored in the right subtree. Duplicate numbers: ** 5 -13

Implementation with C struct nodetype{ int info; struct nodetype *left; struct nodetype *right; }; typedef struct nodetype *NODEPTR; main() { NODEPTR ptree; NODEPTR p, q; int number; scanf("%d", &number); ptree = maketree(number); 5 -14

while (scanf("%d", &number) != EOF){ p = q = ptree; while (number != p->info && q != NULL){ p = q; 14 if (number < p->info) 4 15 q = p->left; else 9 q = p->right; } /* end while */ 7 if (number == p->info) printf("%d is a duplicaten", number); else if (number < p->info) setleft(p, number); else setright(p, number); } /* end while */ } /* end main */ 5 -15

Traversals in a binary tree (1) preorder (depth-first order) 1) root 2) left subtree 3) right subtree (2) inorder (symmetric order) 1) left subtree 2) root 3) right subtree (3) postorder 1) left subtree 2) right subtree 3) root 5 -16

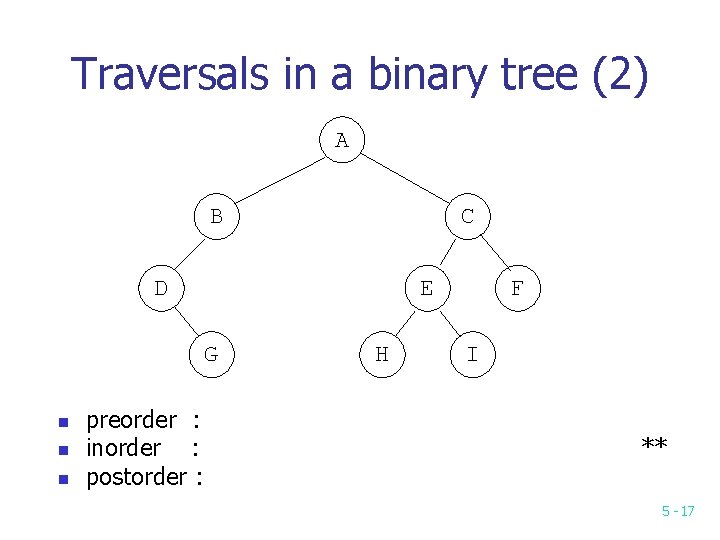
Traversals in a binary tree (2) A B C D E G n n n preorder : inorder : postorder : H F I ** 5 -17

Preorder traversal void pretrav(NODEPTR tree) { if (tree != NULL){ printf("%dn", tree->info); // visit the root pretrav(tree->left); // traverse left subtree pretrav(tree->right); // traverse right subtree } /* end if */ } /* end pretrav */ 5 -18

Inorder traversal void intrav(NODEPTR tree) { if (tree != NULL){ intrav(tree->left); // traverse left subtree printf("%dn", tree->info); // visit the root intrav(tree->right); // traverse right subtree } /* end if */ } /* end intrav */ 5 -19

Postorder traversal void posttrav(NODEPTR tree) { if (tree != NULL){ posttrav(tree->left); //traverse left subtree posttrav(tree->right); //traverse right subtree printf("%dn", tree->info); // visit the root } /* end if */ } /* end posttrav */ 5 -20

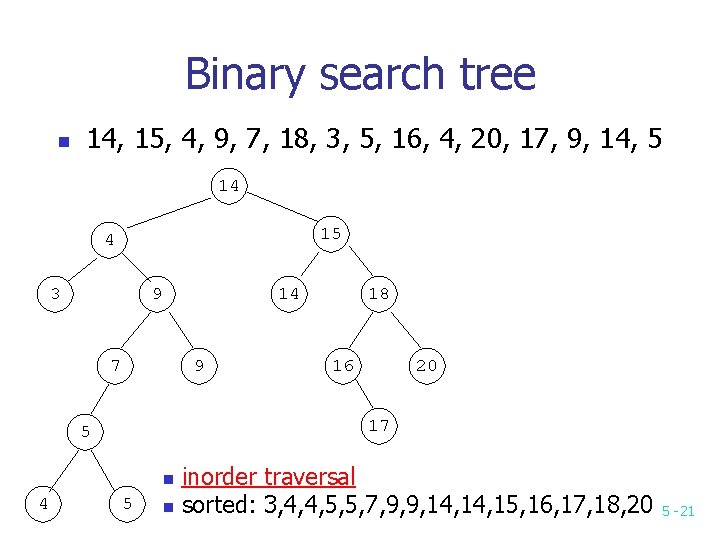
Binary search tree n 14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5 14 15 4 3 9 14 7 9 16 20 17 5 n 4 18 5 n inorder traversal sorted: 3, 4, 4, 5, 5, 7, 9, 9, 14, 15, 16, 17, 18, 20 5 -21

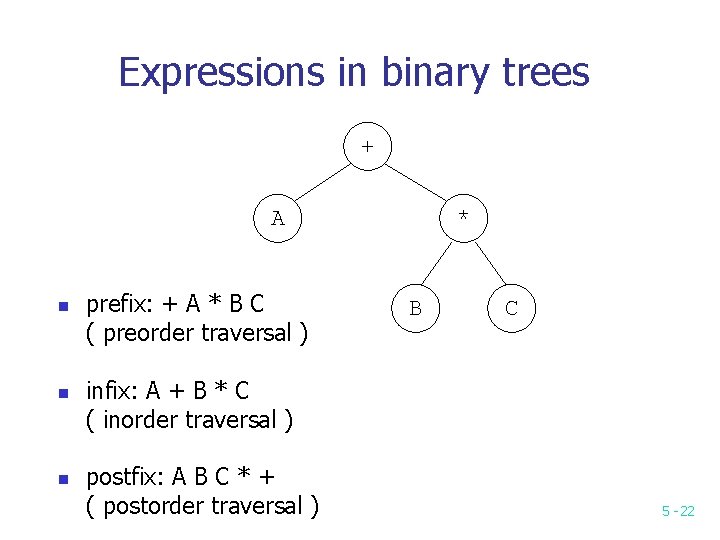
Expressions in binary trees + A n n n prefix: + A * B C ( preorder traversal ) * B C infix: A + B * C ( inorder traversal ) postfix: A B C * + ( postorder traversal ) 5 -22

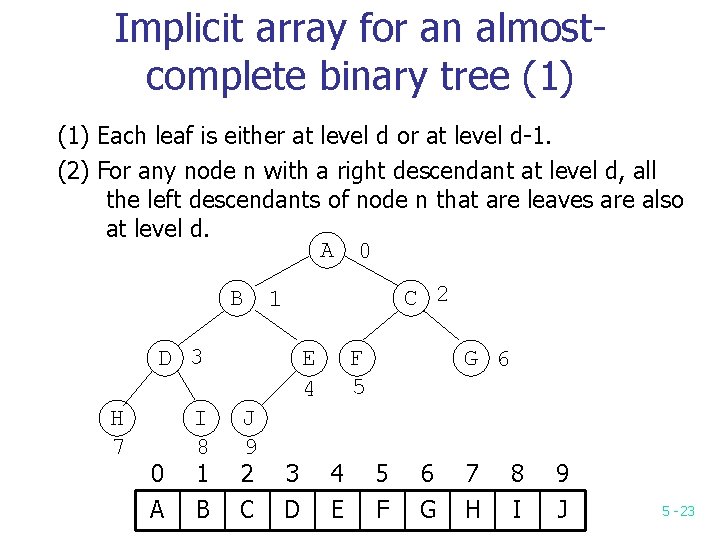
Implicit array for an almostcomplete binary tree (1) Each leaf is either at level d or at level d-1. (2) For any node n with a right descendant at level d, all the left descendants of node n that are leaves are also at level d. A 0 B C 2 1 D 3 H 7 0 A I 8 1 B E 4 J 9 2 C 3 D F 5 4 E G 6 5 F 6 G 7 H 8 I 9 J 5 -23

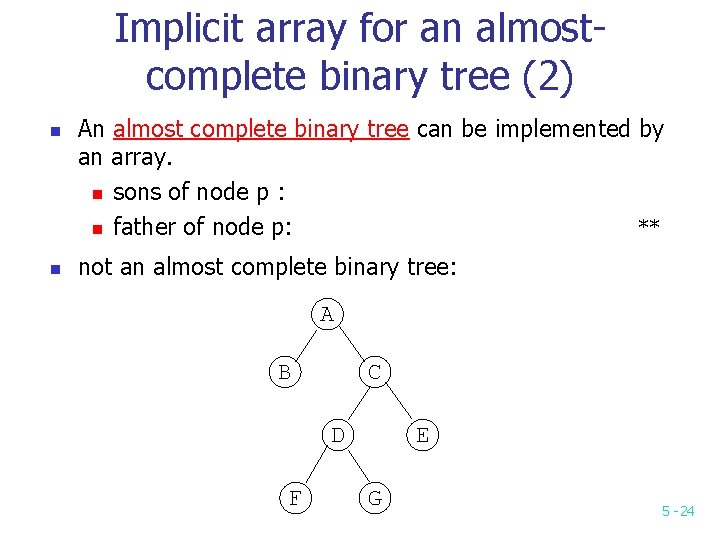
Implicit array for an almostcomplete binary tree (2) n n An almost complete binary tree can be implemented by an array. n sons of node p : n father of node p: ** not an almost complete binary tree: A B C D F E G 5 -24

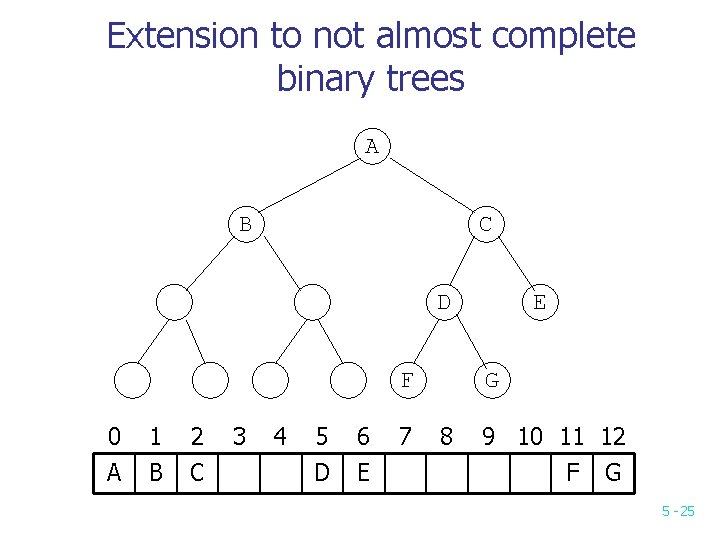
Extension to not almost complete binary trees A B C D F 0 A 1 B 2 C 3 4 5 D 6 E 7 E G 8 9 10 11 12 F G 5 -25

Nonrecursive inorder traversal #define MAXSTACK 100 void intrav 2(NODEPTR tree) { struct stack{ int top; NODEPTR item[MAXSTACK]; }s; NODEPTR p; s. top = -1; p = tree; do{ /*travel down left branches as far as possible */ /* saving pointers to nodes passed */ while (p != NULL){ push(s, p); p = p->left; } /* end while */ 5 -26

/* check if finished */ if (!empty(s)){ /* at this point the left subtree is empty */ p = pop(s); printf("%dn", p->info); /* visit the root */ p = p->right; /* traverse right subtree */ } /* end if */ } while (!empty(s) || p != NULL); } /* end intrav 2 */ n The recursion stack cannot be eliminated. 5 -27

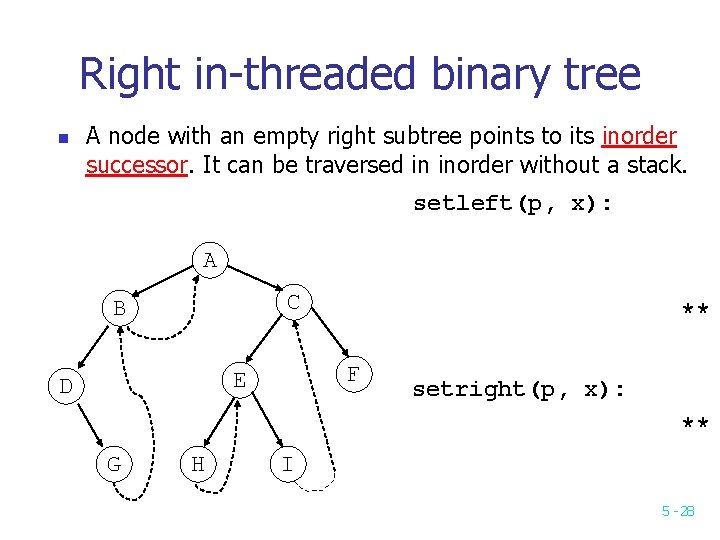
Right in-threaded binary tree n A node with an empty right subtree points to its inorder successor. It can be traversed in inorder without a stack. setleft(p, x): A C B F E D ** setright(p, x): ** G H I 5 -28

Implementation of a right inthreaded binary tree n If the array implementation is used, n n n positive pointer: normal right son negative pointer: inorder successor dynamic implementation: struct nodetype{ int info; struct nodetype *left; // pointer to left son struct nodetype *right; // pointer to right son int rthread; // rthread is TRUE if // right is NULL or } // a non-NULL thread typedef struct nodetype *NODEPTR; 5 -29

Implementation with C (1) void intrav 3(NODEPTR tree) // No stack is used { NODEPTR p, q; p = tree; do{ q = NULL while (p != NULL){ /* traverse left branch */ q = p; p = p->left; } /* end while */ 5 -30

Implementation with C (2) if (q != NULL){ printf("%dn", q->info); p = q->right; while (q->rthread && p != NULL){ printf("%dn", p->info); q = p; p = p->right; } /* end while */ } /* end if */ }while (q != NULL) } /* end intrav 3 */ 5 -31

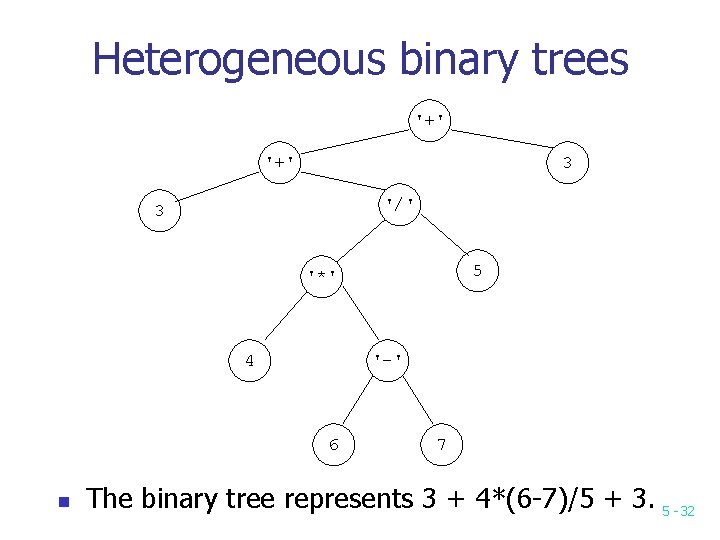
Heterogeneous binary trees '+' 3 '/' 3 5 '*' 4 '-' 6 n 7 The binary tree represents 3 + 4*(6 -7)/5 + 3. 5 -32

Evaluation of an expression represented by a binary tree (1) #define OPERATOR 0 #define OPERAND 1 struct nodetype{ short int utype; /* OPERATOR or OPERAND */ union{ char chinfo; float numinfo; }info; struct nodetype *left; struct nodetype *right; }; typedef struct nodetype *NODEPTR; float evalbintree(NODEPTR tree) { float opnd 1, opnd 2; char symb; 5 -33

Evaluation of an expression represented by a binary tree(2) if (tree->utype == OPERAND) /* expression is a single */ return (tree->numinfo); /* operand */ /* tree->utype == OPERATOR */ /* evaluate the left subtree */ opnd 1 = evalbintree(tree->left); /* evaluate the right subtree */ opnd 2 = evalbintree(tree->right); symb = tree->chinfo; /* extract the operator */ /* apply the operator and return the result */ return(oper(symb, opnd 1, opnd 2)); } /* end evalbintree */ 5 -34

The Huffman code (1) n Suppose we have a set of symbols: A, B, C, D 1) Each symbol is encoded by 3 bits (inefficient) symbol A B C D code 010 100 000 111 Message A B A C C D A would be encoded by 21 bits: 010 100 010 000 111 010 5 -35

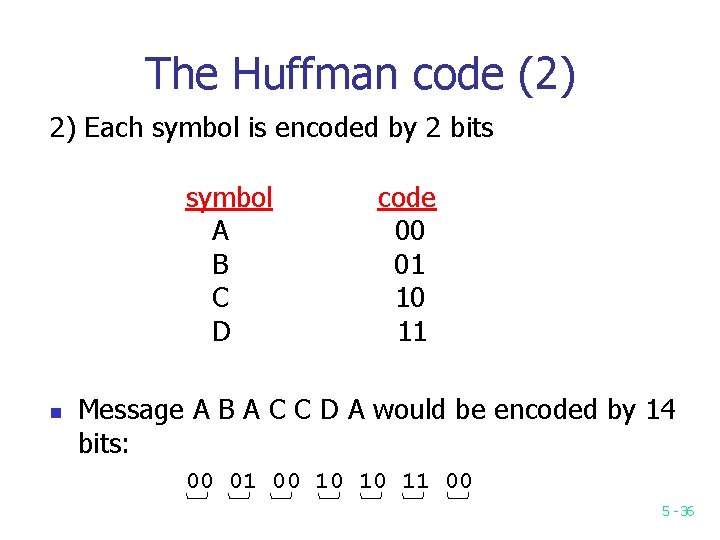
The Huffman code (2) 2) Each symbol is encoded by 2 bits symbol A B C D n code 00 01 10 11 Message A B A C C D A would be encoded by 14 bits: 00 01 00 10 10 11 00 5 -36

The Huffman code (3) 3) Huffman codes (variable-length codes) symbol code A 0 B 110 C 10 D 111 n n Message A B A C C D A would be encoded by 13 bits: 0 110 0 10 10 111 0 A frequently used symbol is encoded by a short bit string. 5 -37

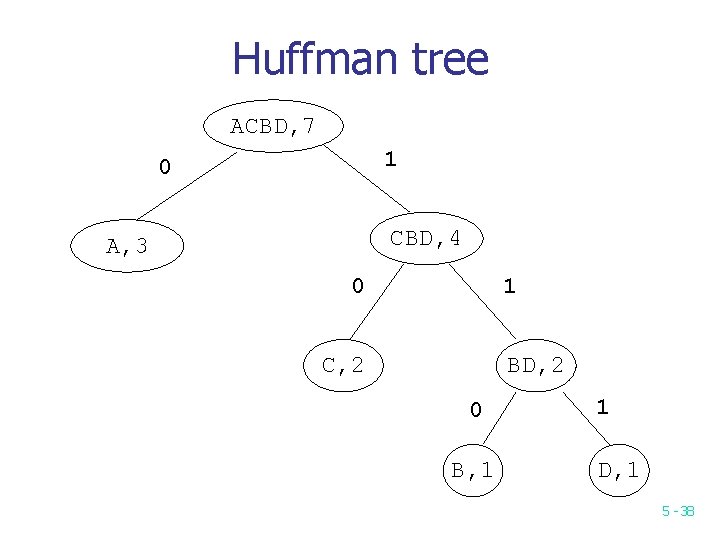
Huffman tree ACBD, 7 1 0 CBD, 4 A, 3 0 1 C, 2 BD, 2 0 B, 1 1 D, 1 5 -38

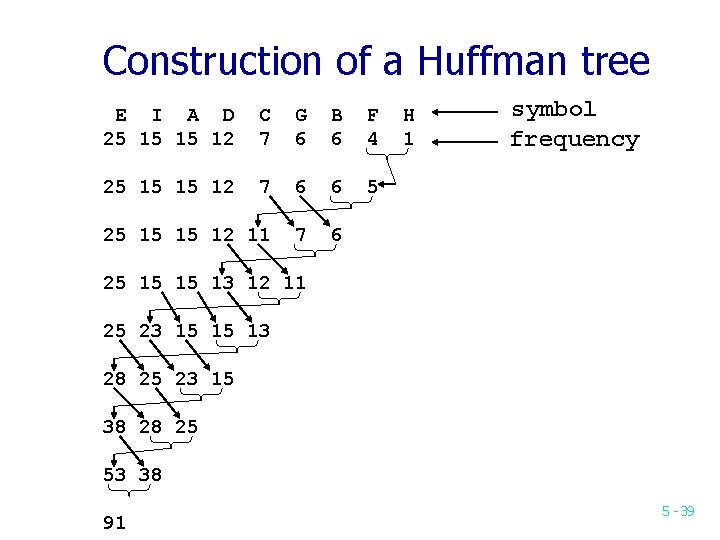
Construction of a Huffman tree E I A D 25 15 15 12 C 7 G 6 B 6 F 4 25 15 15 12 7 6 6 5 25 15 15 12 11 7 6 H 1 symbol frequency 25 15 15 13 12 11 25 23 15 15 13 28 25 23 15 38 28 25 53 38 91 5 -39

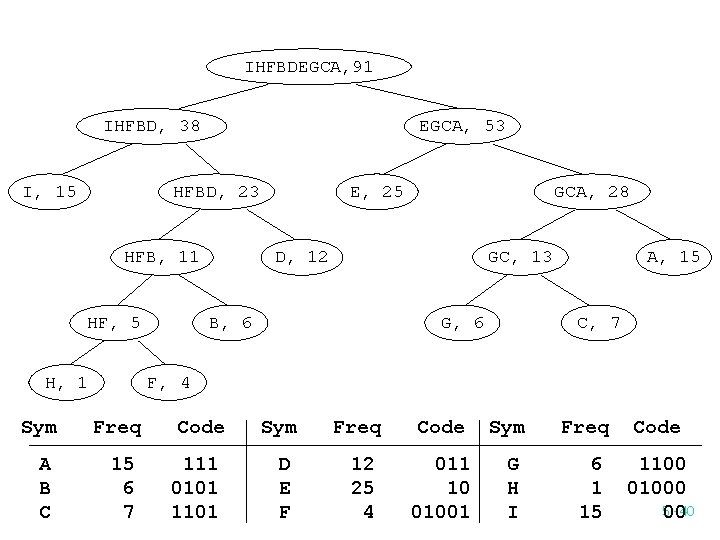
IHFBDEGCA, 91 IHFBD, 38 I, 15 EGCA, 53 HFBD, 23 HFB, 11 HF, 5 H, 1 E, 25 GCA, 28 D, 12 GC, 13 B, 6 G, 6 A, 15 C, 7 F, 4 Sym Freq A B C 15 6 7 Code 111 0101 1101 Sym Freq Code D E F 12 25 4 011 10 01001 G H I 6 1 15 1100 01000 5 -40 00

The result of Huffman coding 111 01000 10 111 011 n decode encode AHEAD A Huffman tree is a strictly binary tree. The Huffman algorithm is an optimal encoding scheme. 5 -41

Representing lists as binary trees (1) array insertion or deletion (kth element) O(n-k) finding the kth element O(1) n linked list O(1) (inserting an element following a given element) O(k) binary tree (balanced) O(log 2 n) n: # of elements 5 -42

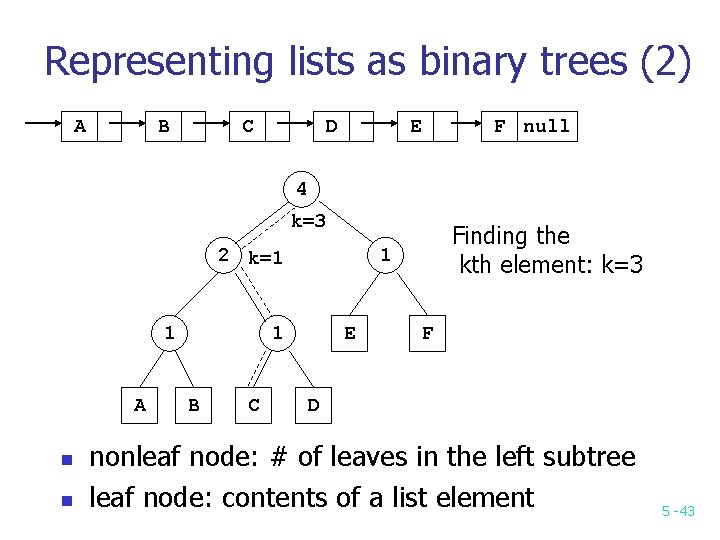
Representing lists as binary trees (2) A B C D E F null 4 k=3 2 k=1 1 A n n 1 1 B C Finding the kth element: k=3 E F D nonleaf node: # of leaves in the left subtree leaf node: contents of a list element 5 -43

Representing lists as binary trees (3) n n A complete binary tree of depth d has 2 d+1 -1 nodes or 2 d leaf nodes. If an almost complete binary tree is used to represent a list, the kth element can be found by accessing O(log 2 n) nodes. 5 -44

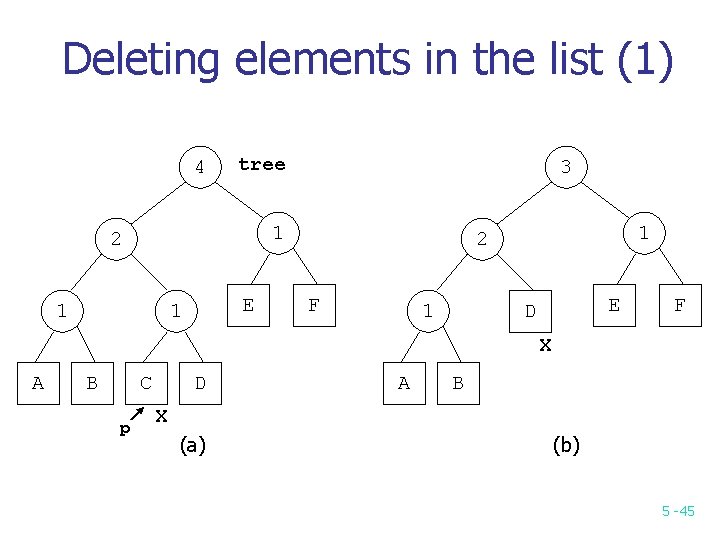
Deleting elements in the list (1) 4 tree 3 1 2 1 E 1 1 2 F E D 1 F X A B C p D A B X (a) (b) 5 -45

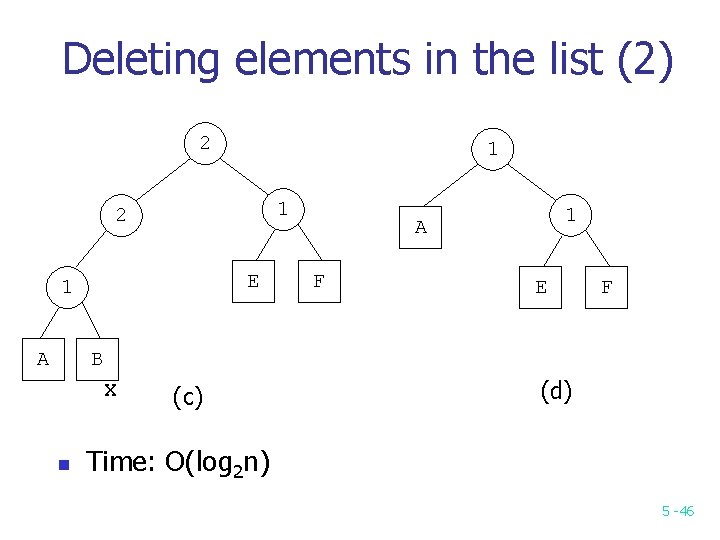
Deleting elements in the list (2) 2 1 1 2 E 1 A F E F B X n (c) (d) Time: O(log 2 n) 5 -46

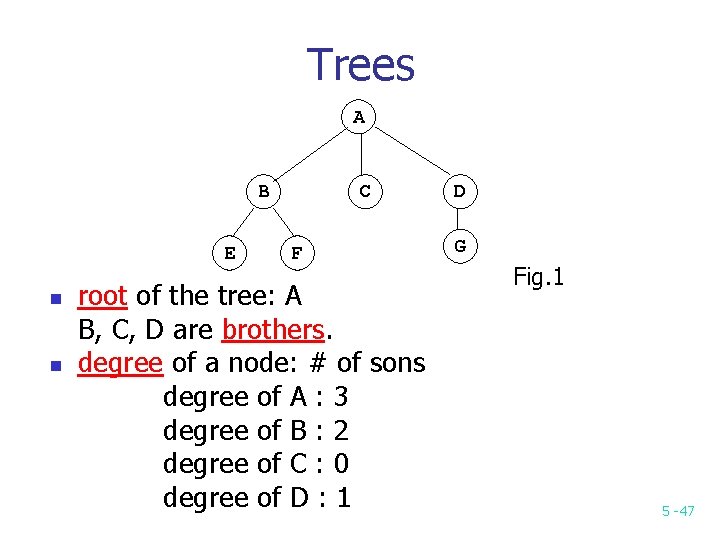
Trees A B E n n C F root of the tree: A B, C, D are brothers. degree of a node: # of sons degree of A : 3 degree of B : 2 degree of C : 0 degree of D : 1 D G Fig. 1 5 -47

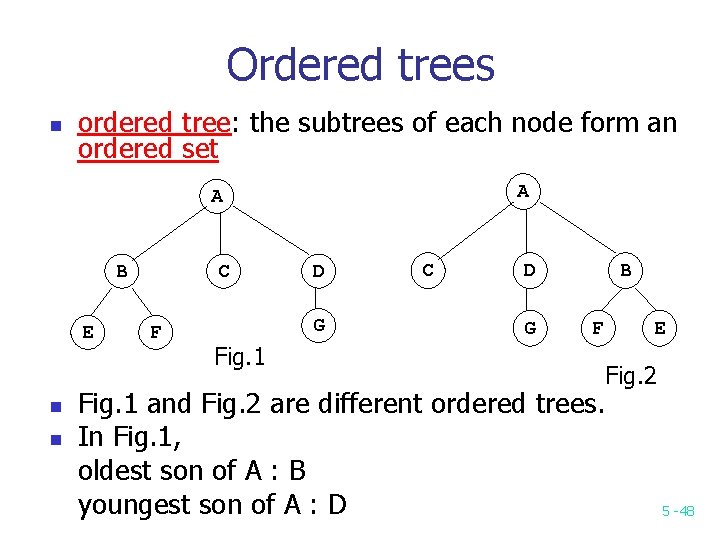
Ordered trees n ordered tree: the subtrees of each node form an ordered set A A B E n n C F D G Fig. 1 C D G B F E Fig. 2 Fig. 1 and Fig. 2 are different ordered trees. In Fig. 1, oldest son of A : B youngest son of A : D 5 -48

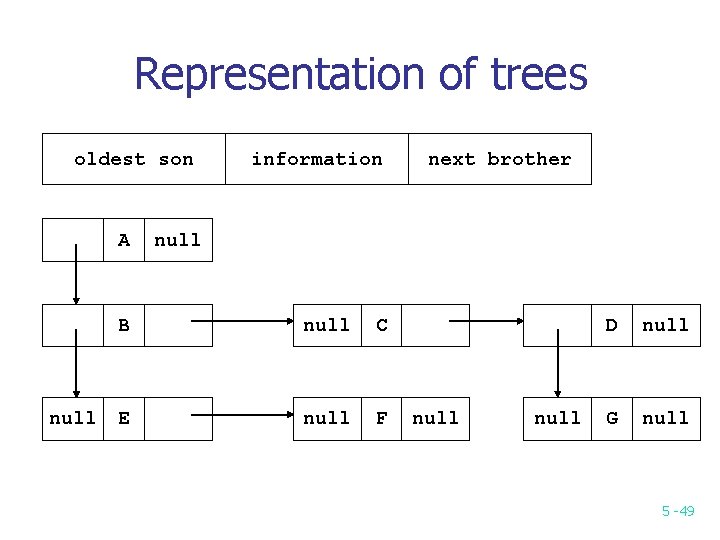
Representation of trees oldest son A null information next brother null B null C E null F null D null G null 5 -49

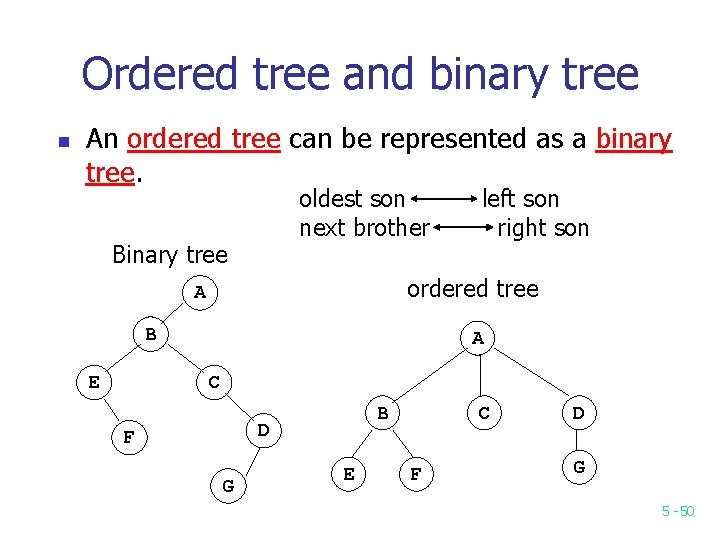
Ordered tree and binary tree n An ordered tree can be represented as a binary tree. oldest son next brother Binary tree ordered tree A B E left son right son A C B D F G E C F D G 5 -50

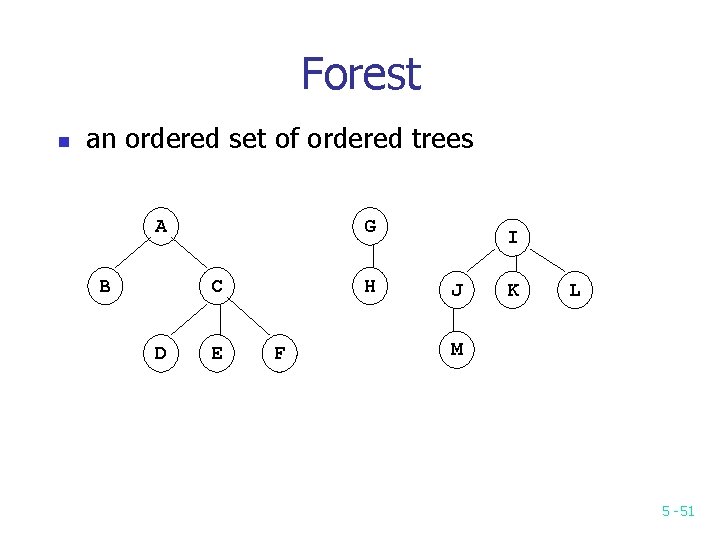
Forest n an ordered set of ordered trees A B G C D E H F I J K L M 5 -51

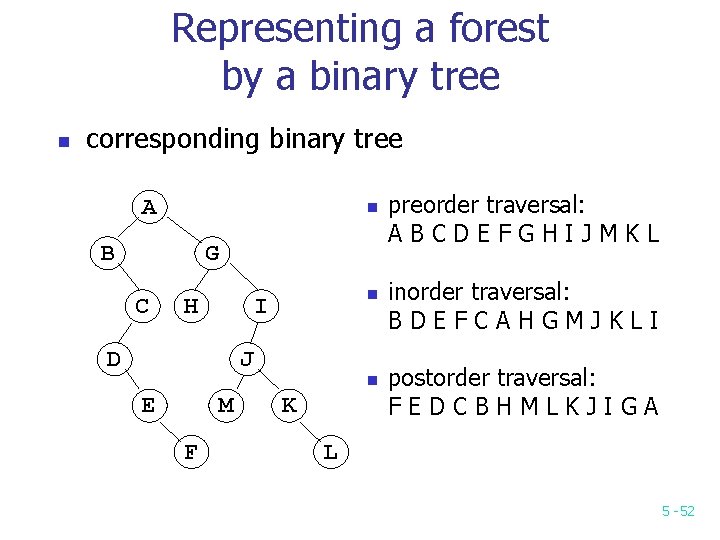
Representing a forest by a binary tree n corresponding binary tree A n B G C H n I D J E M F n K preorder traversal: ABCDEFGHIJMKL inorder traversal: BDEFCAHGMJKLI postorder traversal: FEDCBHMLKJIGA L 5 -52

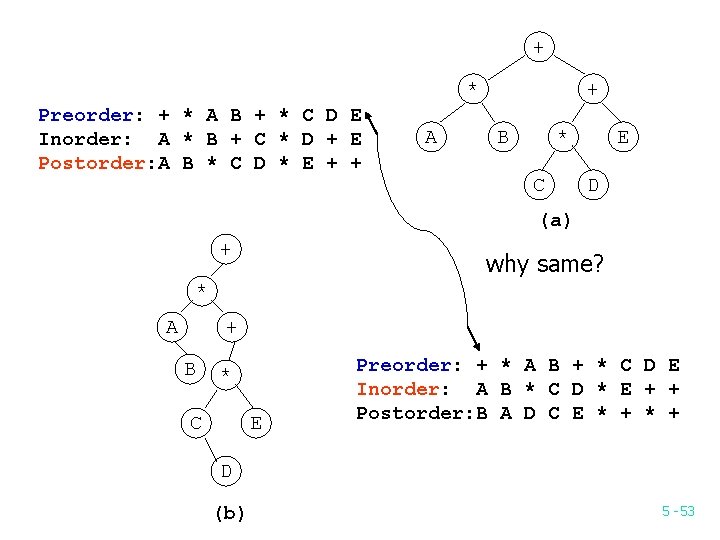
+ * Preorder: + * A B + * C D E Inorder: A * B + C * D + E Postorder: A B * C D * E + + A + B * C E D (a) + why same? * A + B * C E Preorder: + * A B + * C D E Inorder: A B * C D * E + + Postorder: B A D C E * + D (b) 5 -53

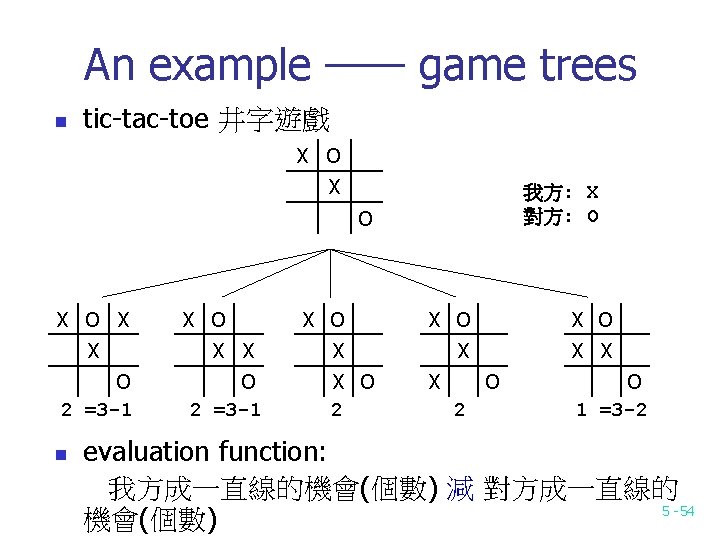
An example —— game trees n tic-tac-toe 井字遊戲 X O X 我方: X 對方: O O X X O 2 =3 -1 n X O X X O 2 =3 -1 X O X O X X X O 2 O 1 =3 -2 evaluation function: 我方成一直線的機會(個數) 減 對方成一直線的 5 -54 機會(個數)

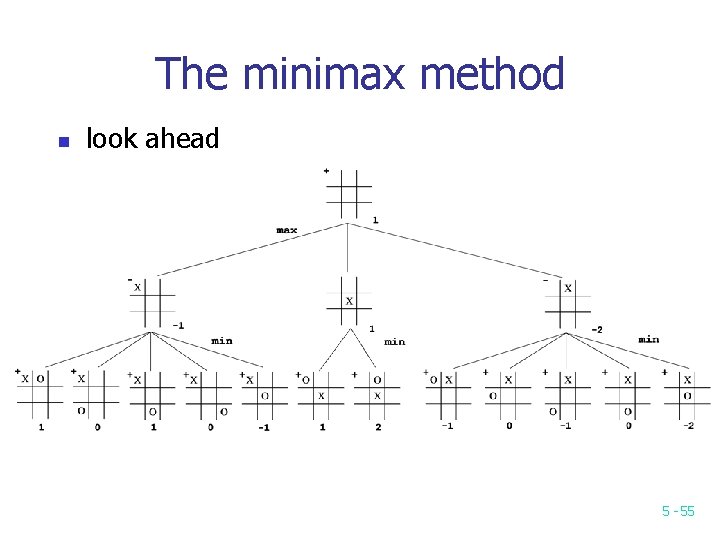
The minimax method n look ahead 5 -55