Chapter 5 transform analysis of linear timeinvariant system

Chapter 5 transform analysis of linear time-invariant system 5. 1 the frequency response of LTI system 5. 2 system function 5. 3 frequency response for rational system function 5. 4 relationship between magnitude and phase 5. 5 all-pass system 5. 6 minimum-phase system 5. 7 linear system with generalized linear phase 1

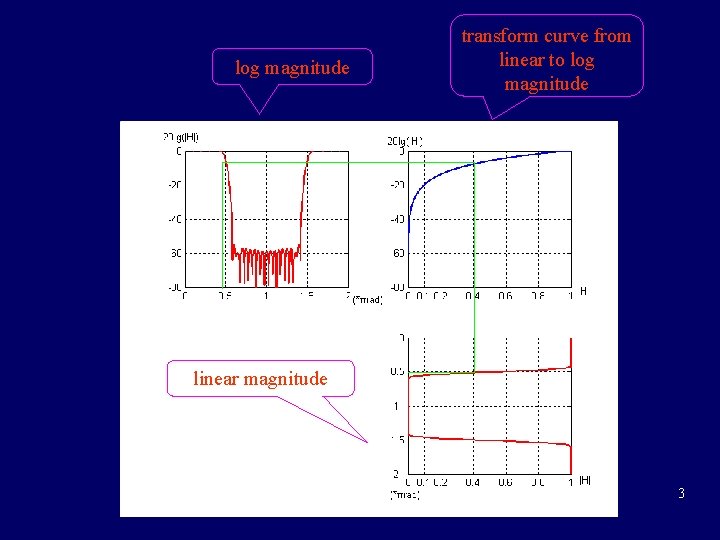
5. 1 the frequency response of LTI system magnitude-frequency characteristic： magnitude response or gain magnitude square function log magnitude attenuation 2

log magnitude transform curve from linear to log magnitude linear magnitude 3

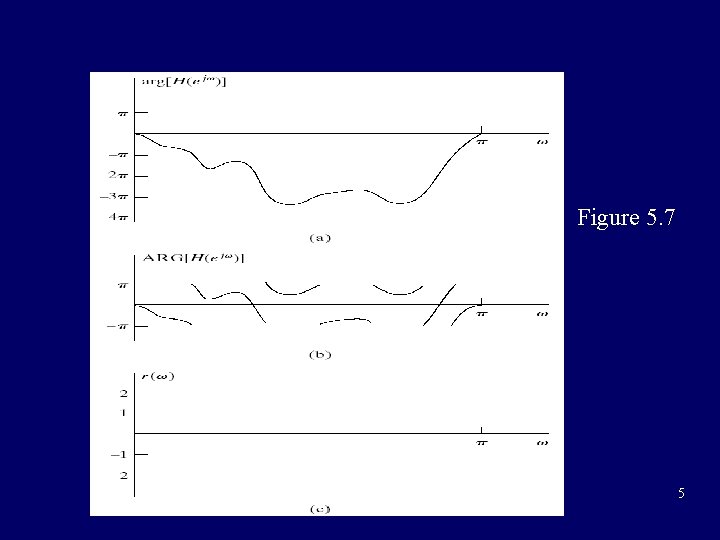
phase-frequency characteristic： phase response principal phase continuous phase group delay 4

Figure 5. 7 5

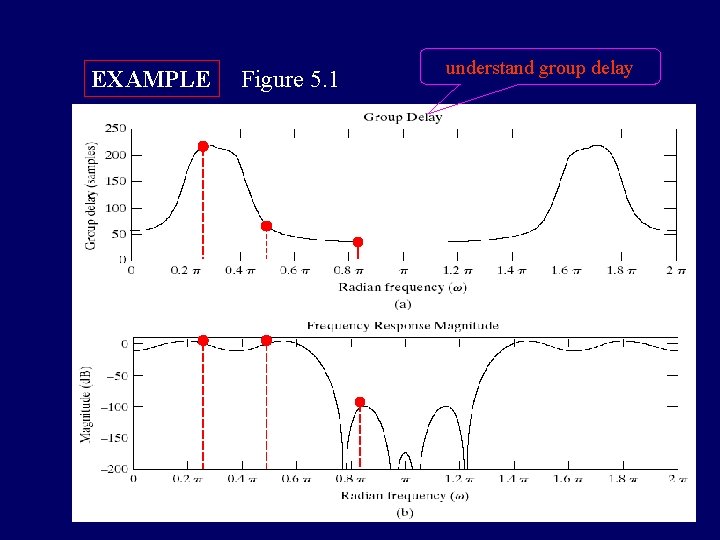
EXAMPLE Figure 5. 1 understand group delay 6

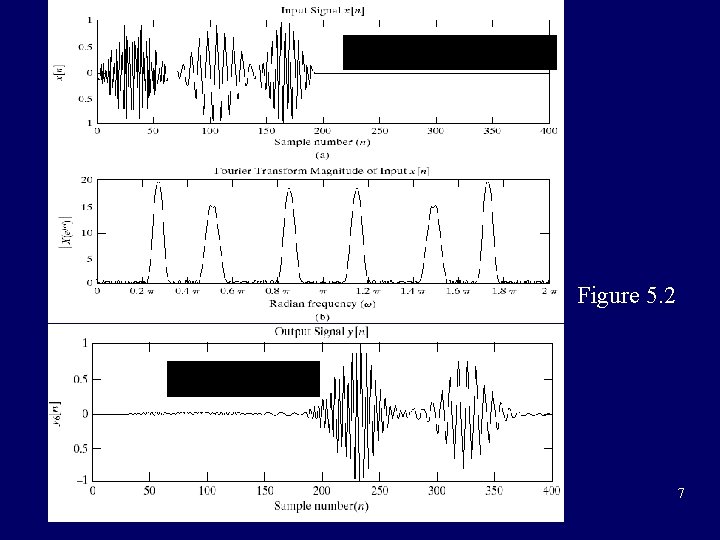
Figure 5. 2 7

5. 2 system function Characteristics of zeros and poles： （1）take origin and zeros and poles at infinite into consideration, the numbers of zeros and poles are the same. （2）for real coefficient, complex zeros and poles are conjugated, respectively. （3）if causal and stable, poles are all in the unit circle. （4）FIR：have no nonzero poles, called all-zeros type, steady IIR：have nonzero pole; if no nonzeros , called all-poles type EXAMPLE Difference about zeros and poles in FIR and IIR 8

5. 3 frequency response for rational system function 1. formular method 9

2. Geometrical method 10

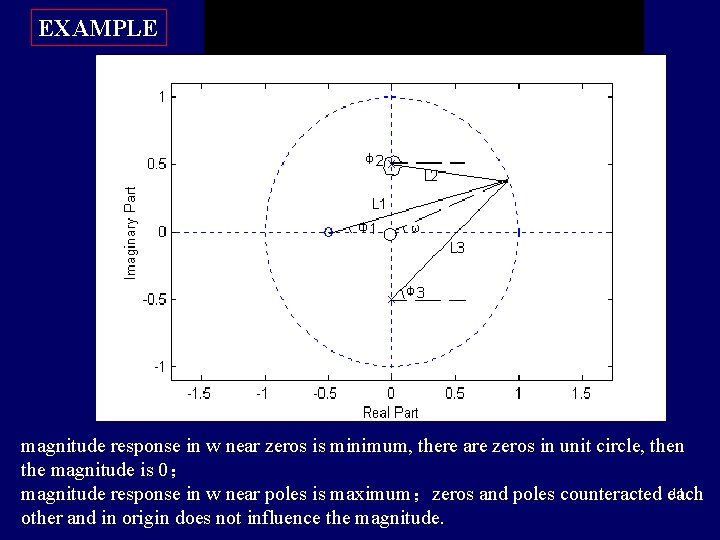
EXAMPLE magnitude response in w near zeros is minimum, there are zeros in unit circle, then the magnitude is 0； 11 magnitude response in w near poles is maximum；zeros and poles counteracted each other and in origin does not influence the magnitude.

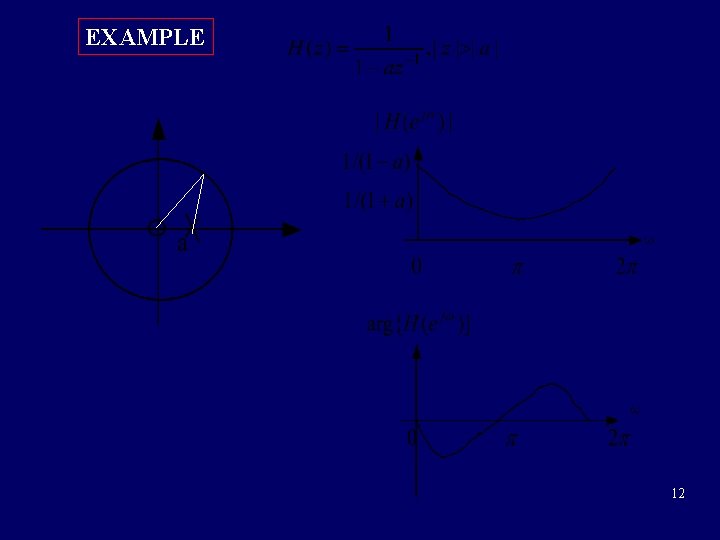
EXAMPLE 12

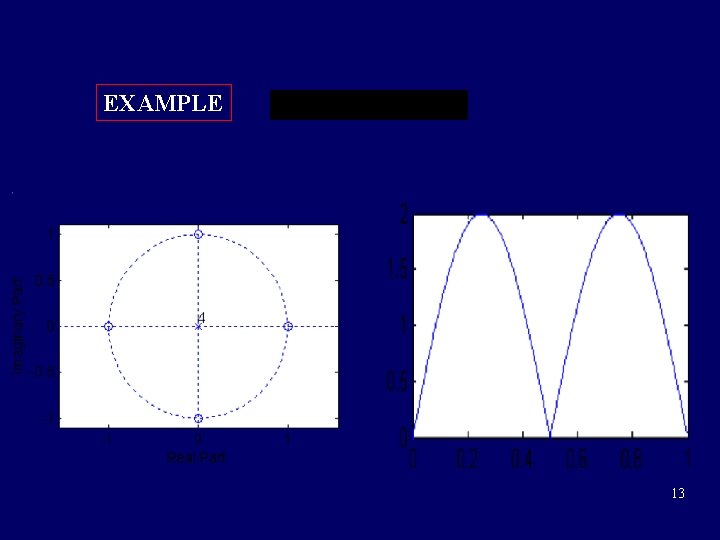
EXAMPLE 13

3. matlab method EXAMPLE B=1 A=[1, -0. 5] figure(1) zplane(B, A) figure(2) freqz(B, A) figure(3) grpdelay(B, A, 10) 14

5. 4 relationship between magnitude and phase 15

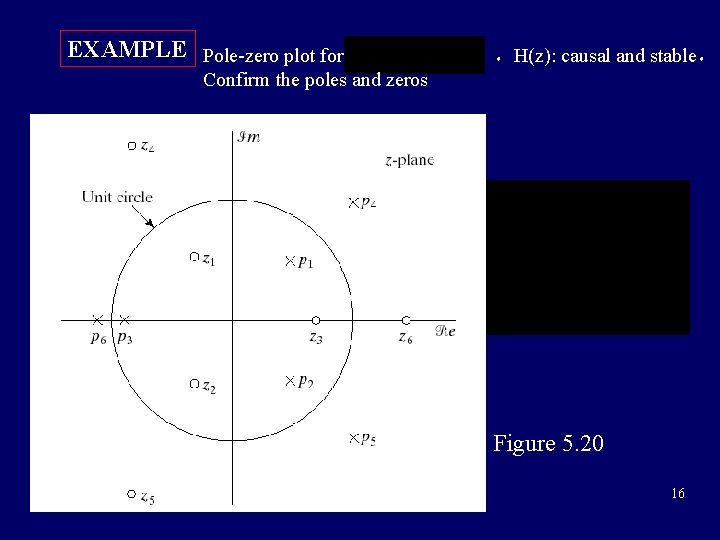
EXAMPLE Pole-zero plot for ，H(z): causal and stable， Confirm the poles and zeros Figure 5. 20 16

5. 5 all-pass system Zeros and poles are conjugate reciprocal For real coefficient, zeros are conjugated , poles are conjugated. 17

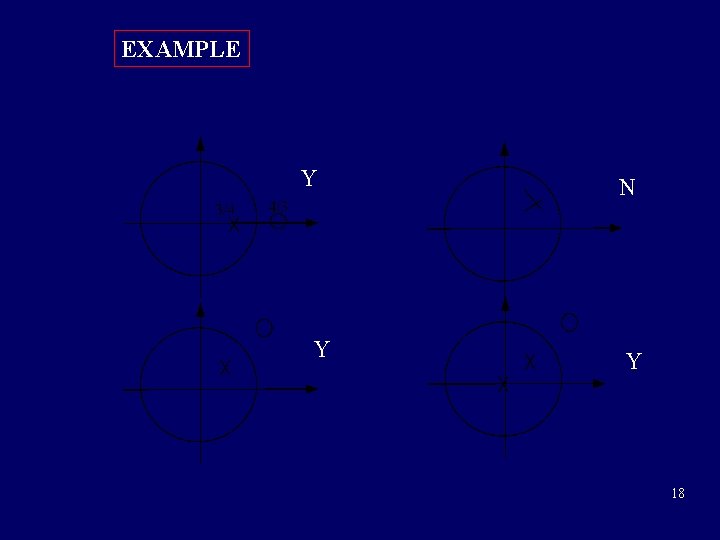
EXAMPLE Y Y N Y 18

Characteristics of causal and stable all-pass system: application： 1. compensate the phase distortion 2. compensate the magnitude distortion together with minimum-phase system 19

5. 6 minimum-phase system inverse system: 20

explanation： （1）not all the systems have inverse system。 （2）inverse system may be nonuniform。 （3）the inverse system of causal and stable system may not be causal and stable。 the condition of both original and its inverse system causal and stable： zeros and poles are all in the unit circle，such system is called minimumphase system, corresponding h[n] is minimum-phase sequence。 poles are all in the unit circle, zeros are all outside the unit circle, such system is called maximum-phase system。 21

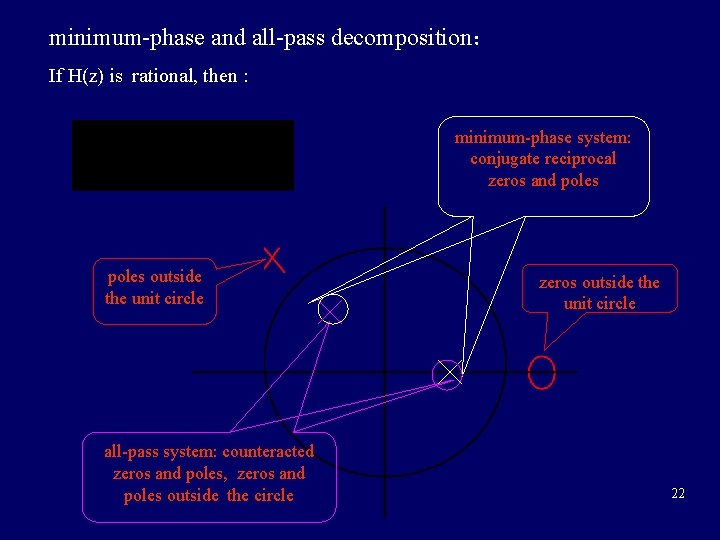
minimum-phase and all-pass decomposition： If H(z) is rational, then : minimum-phase system: conjugate reciprocal zeros and poles outside the unit circle all-pass system: counteracted zeros and poles, zeros and poles outside the circle zeros outside the unit circle 22

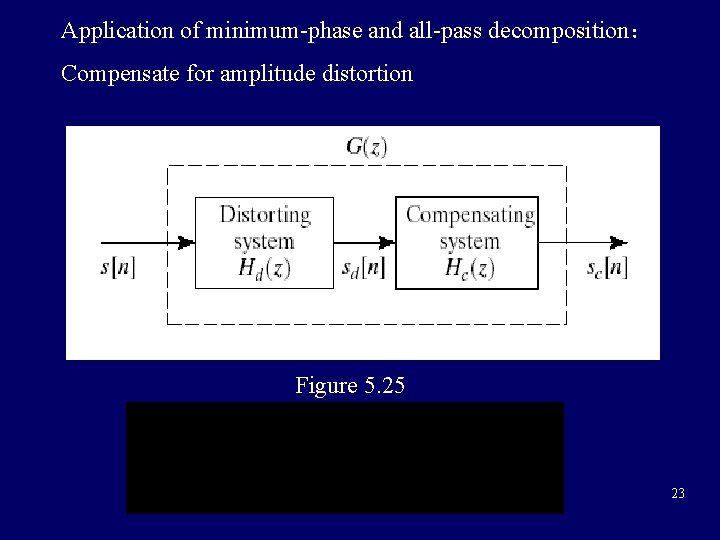
Application of minimum-phase and all-pass decomposition： Compensate for amplitude distortion Figure 5. 25 23

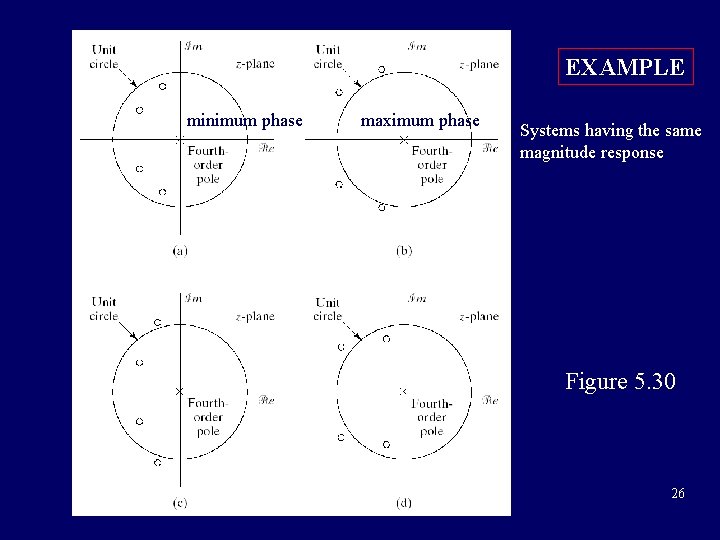
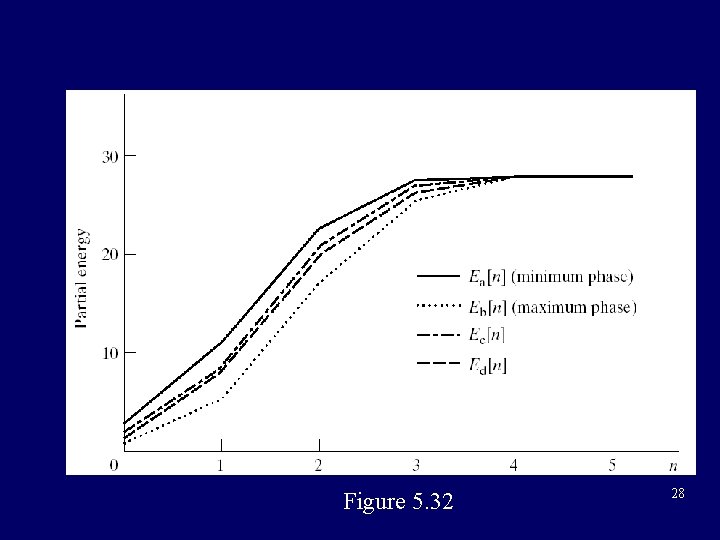
Minimum-phase system and some all-pass system in cascade can make up of another system having the same magnitude response, so there are infinite systems having the same magnitude response. Properties of minimum-phase systems: （1）minimum phase-delay （2）minimum group-delay 24

（3）minimum energy-delay（i. e. the partial energy is most concentrated around n=0） 25

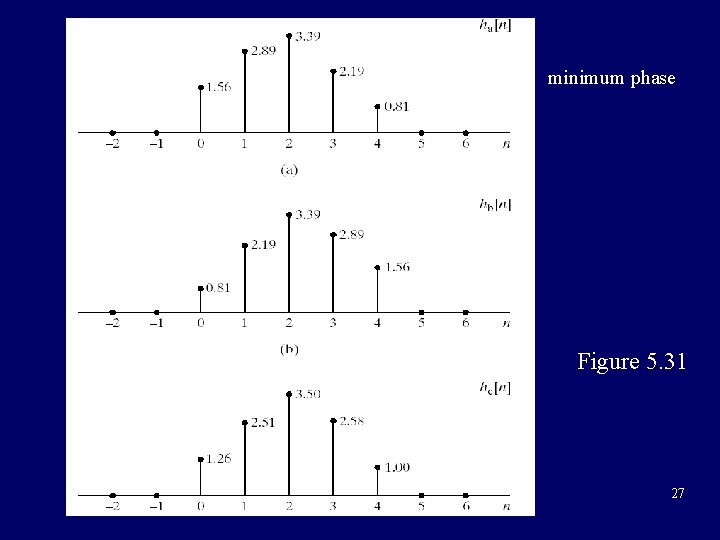
EXAMPLE 最小相位 minimum phase maximum phase Systems having the same magnitude response Figure 5. 30 26

minimum phase Figure 5. 31 27

Figure 5. 32 28

5. 7 linear system with generalized linear phase 5. 7. 1 definition 5. 7. 2 conditions of generalized linear phase system 5. 7. 3 causal generalized linear phase (FIR)system 29

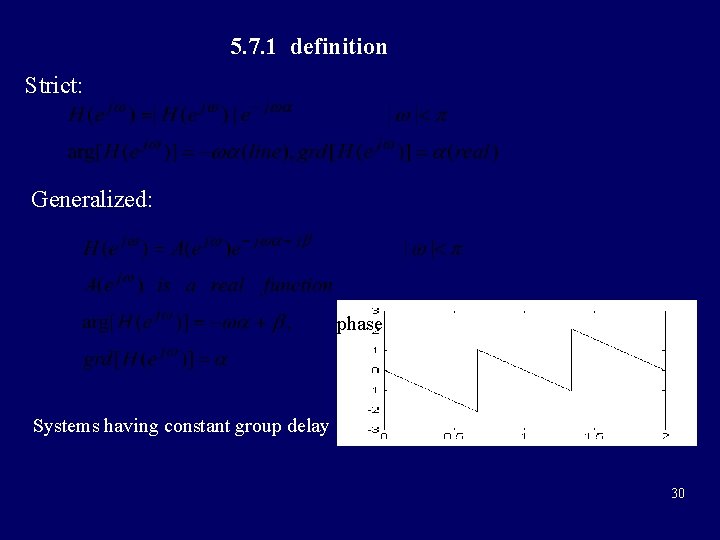
5. 7. 1 definition Strict: Generalized: phase Systems having constant group delay 30

EXAMPLE ideal delay system differentiator：magnitude and phase are all linear physical meaning： all components of input signal are delayed by the same amount in strict linear phase system ，then there is only magnitude distortion, no phase distortion. it is very important for image signal and high-fidelity audio signal to have no phase distortion. when B=0, for generalized linear phase, the phase in the whole band is not linear, but is linear in the pass band, because the phase +PI only occurs when 31 magnitude is 0, and the magnitude in the pass band is not 0.

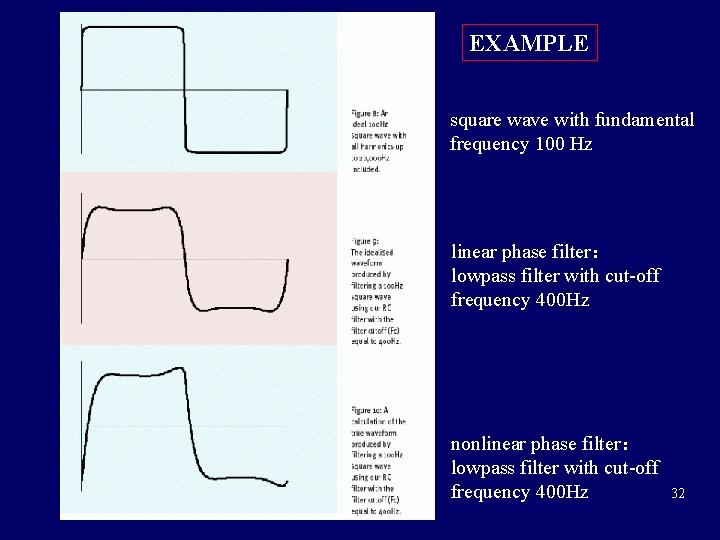
EXAMPLE square wave with fundamental frequency 100 Hz linear phase filter： lowpass filter with cut-off frequency 400 Hz nonlinear phase filter： lowpass filter with cut-off frequency 400 Hz 32

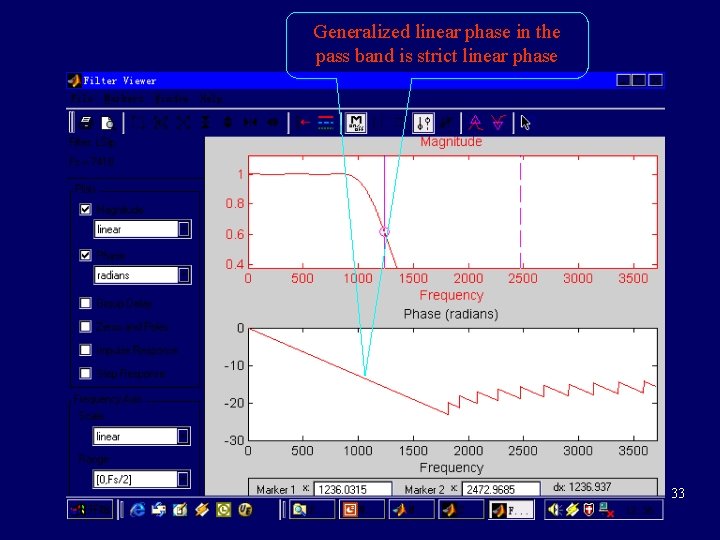
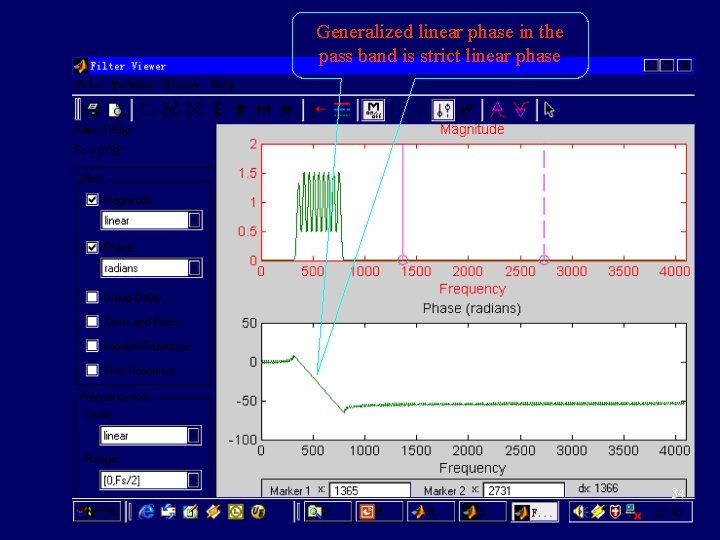
Generalized linear phase in the pass band is strict linear phase 33

Generalized linear phase in the pass band is strict linear phase 34

5. 7. 2 conditions of generalized linear phase system Or: 35

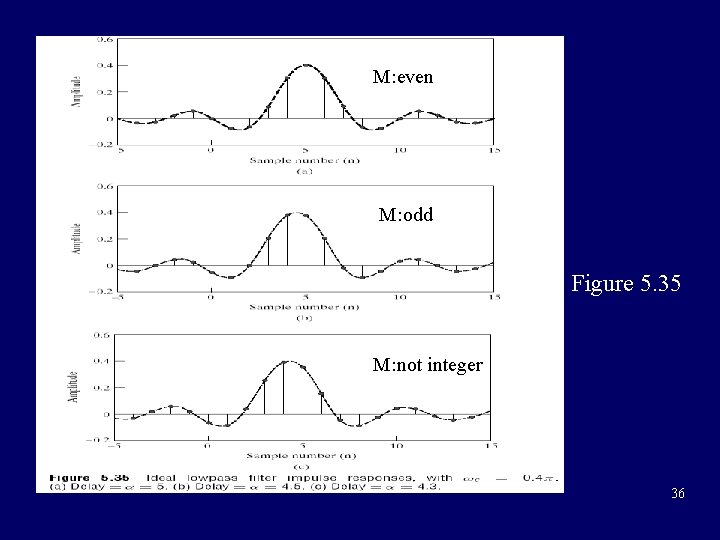
M: even M: odd Figure 5. 35 M: not integer 36

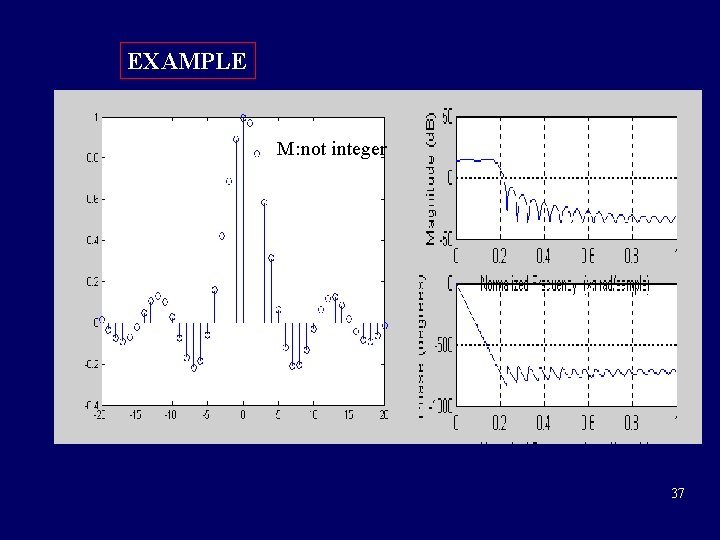
EXAMPLE M: not integer 37

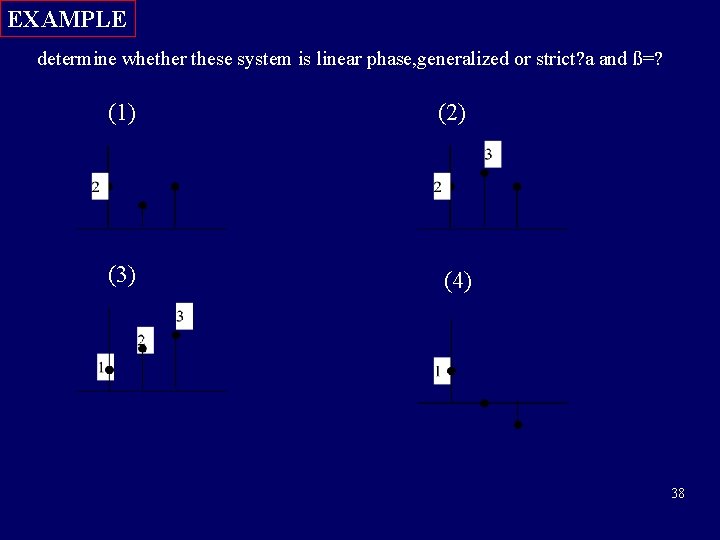
EXAMPLE determine whether these system is linear phase, generalized or strict? a and ß=? (1) (2) (3) (4) 38

5. 7. 3 causal generalized linear phase (FIR)system 39

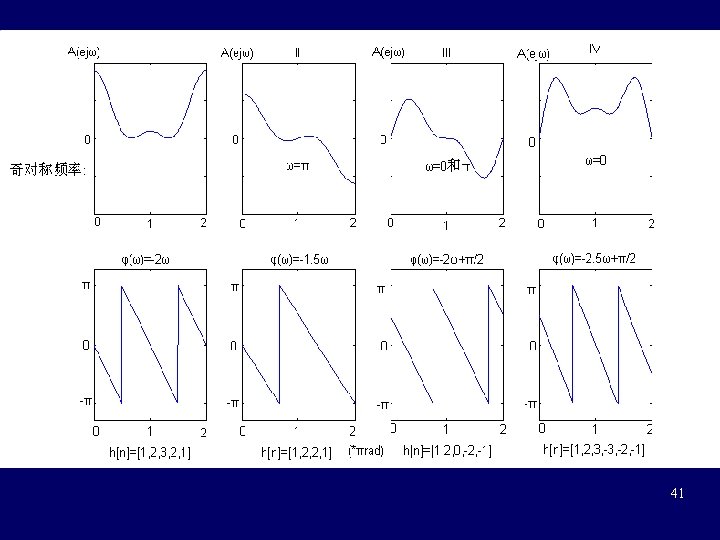
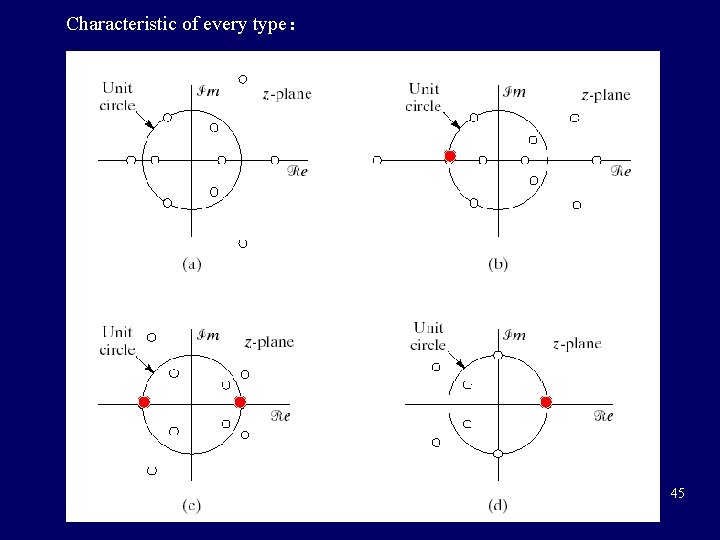
Magnitude and phase characteristics of the 4 types： 40

41

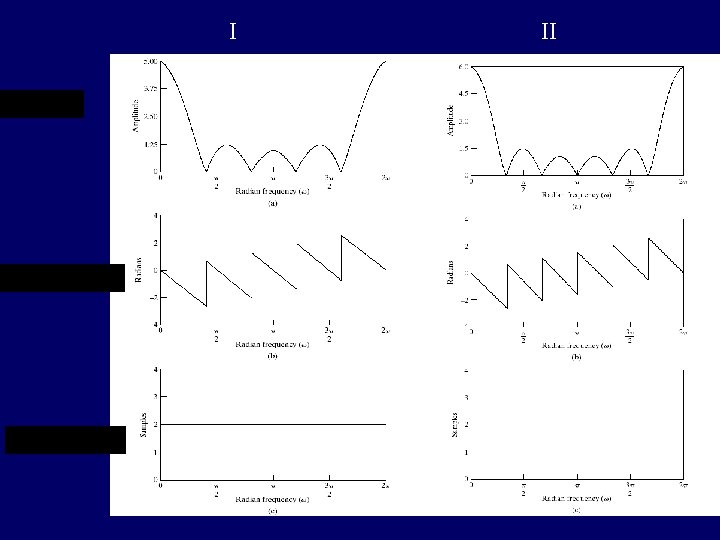
I II 42

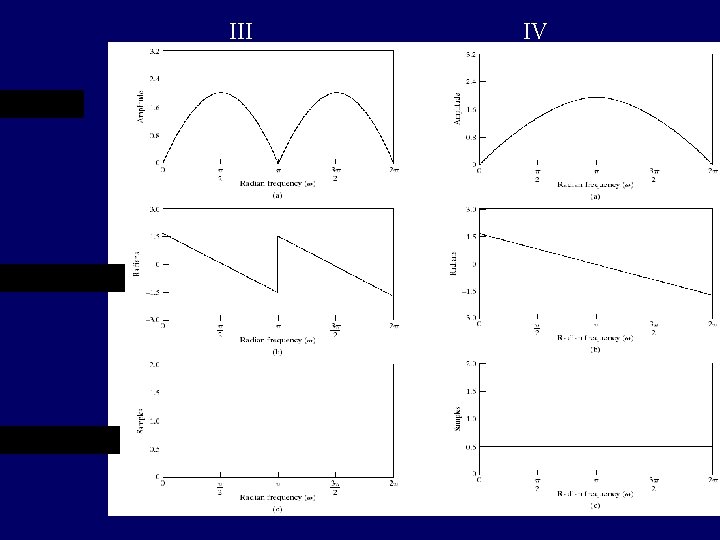
III IV 43

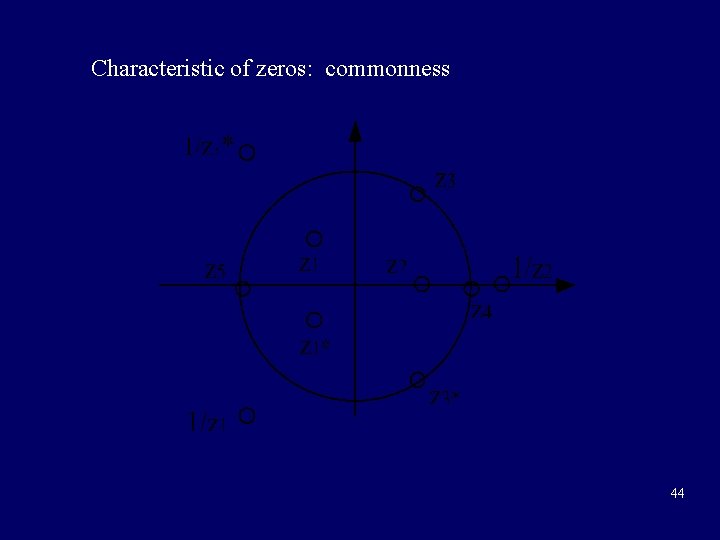
Characteristic of zeros: commonness 44

Characteristic of every type： Figure 5. 41 45

characteristic of magnitude get from characteristic of zeros： type II： type III： type IV： 46

Application of 4 types of linear phase system: M is even M is odd low high band pass band stop h[n] is even (I) Y Y Y N h[n] is odd (III) N Y N N Y Y N (IV) N (II) 47

summary 5. 1 the frequency response of LTI system : 5. 2 system function 5. 3 frequency response for rational system function: 5. 4 relationship between magnitude and phase : 5. 5 all-pass system 5. 6 minimum-phase system 5. 7 linear system with generalized linear phase （FIR) 5. 7. 1 definition: 5. 7. 2 conditions : h[n] is symmetrical 5. 7. 3 causal generalized linear phase system 1. condition 2. classification 3. characteristics of magnitude and phase , filters in point respectively 4. analyse of characteristic of magnitude from the zeros of system function 48

requirement: concept of magnitude and phase response, group delay; transformation among system function, phase response and difference equation; concept of all-pass, minimum-phase and linear phase system and characteristic of zeros and poles; minimum-phase and all-pass decomposition; conditions of linear phase system , restriction of using as filters key and difficulty： linear phase system 49

exercises 5. 17 complementarity：minimum-phase and all-pass decomposition 5. 21 5. 45 5. 53 50

the first experiment Get subjects from the experiment instruction book or downloading from network： problem 1（D） problem 11 problem 13（C） problem 22（A） problem 24（A）（C） 51