CHAPTER 5 The Straight Line Learning Objectives 5

CHAPTER 5 The Straight Line

Learning Objectives 5. 1 Understand the concept of gradient of a straight line. 5. 2 Understand the concept of gradient of a straight line in Cartesian coordinates. 5. 3 Understand the concept of intercept. 5. 4 Understand use equation of a straight line. 5. 5 Understand use the concept of parallel lines.
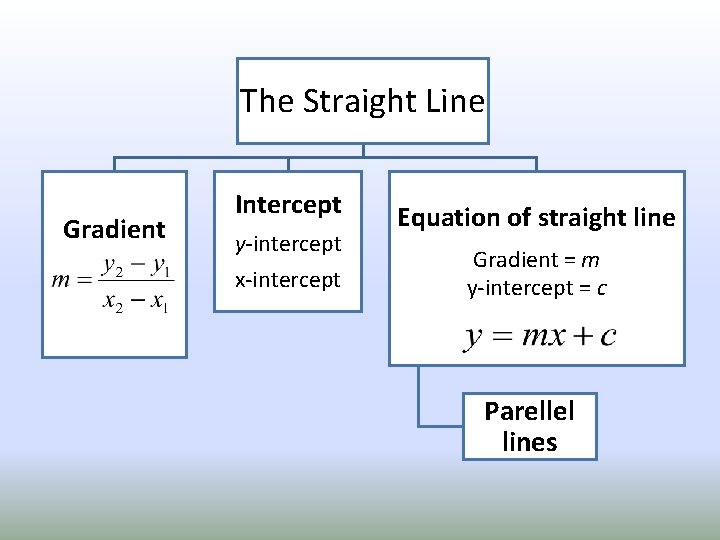
The Straight Line Gradient Intercept y-intercept x-intercept Equation of straight line Gradient = m y-intercept = c Parellel lines
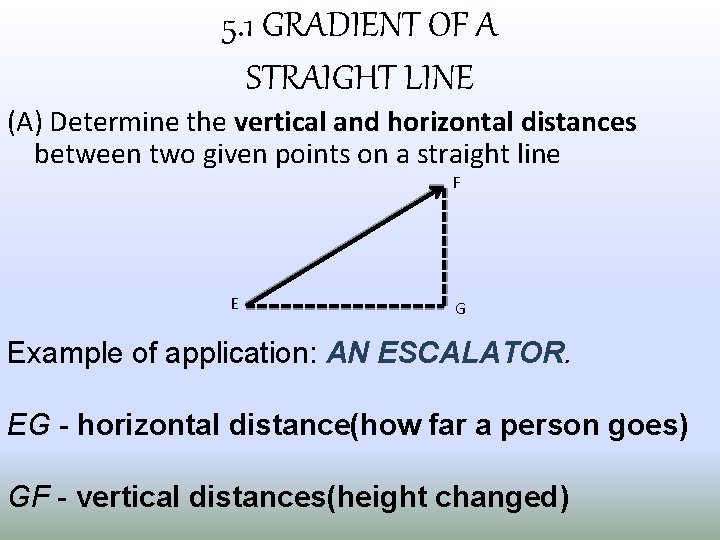
5. 1 GRADIENT OF A STRAIGHT LINE (A) Determine the vertical and horizontal distances between two given points on a straight line F E G Example of application: AN ESCALATOR. EG - horizontal distance(how far a person goes) GF - vertical distances(height changed)

Example 1 State the horizontal and vertical distances for the following case. 10 m 16 m Solution: The horizontal distance = 16 m The vertical distance = 10 m
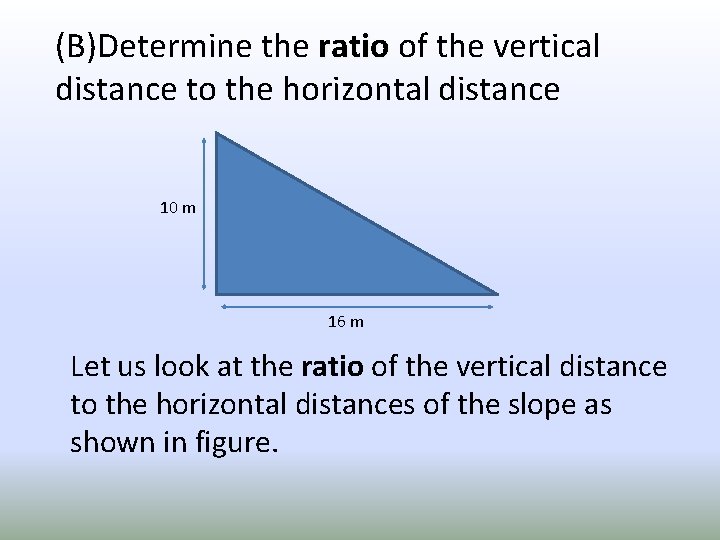
(B)Determine the ratio of the vertical distance to the horizontal distance 10 m 16 m Let us look at the ratio of the vertical distance to the horizontal distances of the slope as shown in figure.

Vertical distance = 10 m Horizontal distance = 16 m Therefore, Solution:
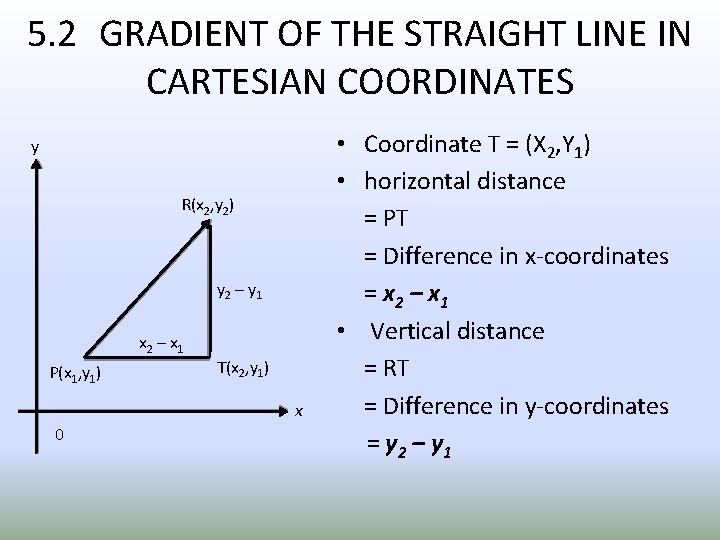
5. 2 GRADIENT OF THE STRAIGHT LINE IN CARTESIAN COORDINATES y R(x 2, y 2) y 2 – y 1 x 2 – x 1 P(x 1, y 1) T(x 2, y 1) x 0 • Coordinate T = (X 2, Y 1) • horizontal distance = PT = Difference in x-coordinates = x 2 – x 1 • Vertical distance = RT = Difference in y-coordinates = y 2 – y 1

Solution: REMEMBER!!! For a line passing through two points (x 1, y 1) and (x 2, y 2), where m is the gradient of a straight line

Example 2 • Determine the gradient of the straight line passing through the following pairs of points i) P(0, 7) , Q(6, 10) ii) L(6, 1) , N(9, 7) Solution:

(C) Determine the relationship between the value of the gradient and the (i)Steepness (ii)Direction of inclination of a straight line • What does gradient represents? ? Steepness of a line with respect to the x-axis.
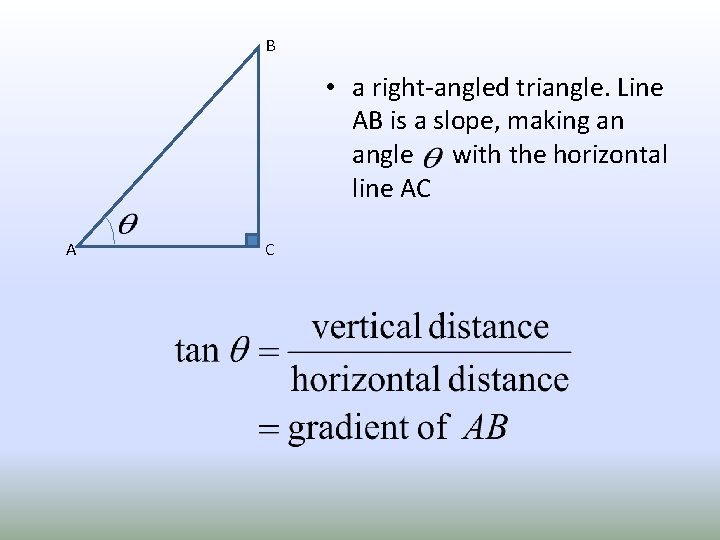
B • a right-angled triangle. Line AB is a slope, making an angle with the horizontal line AC A C
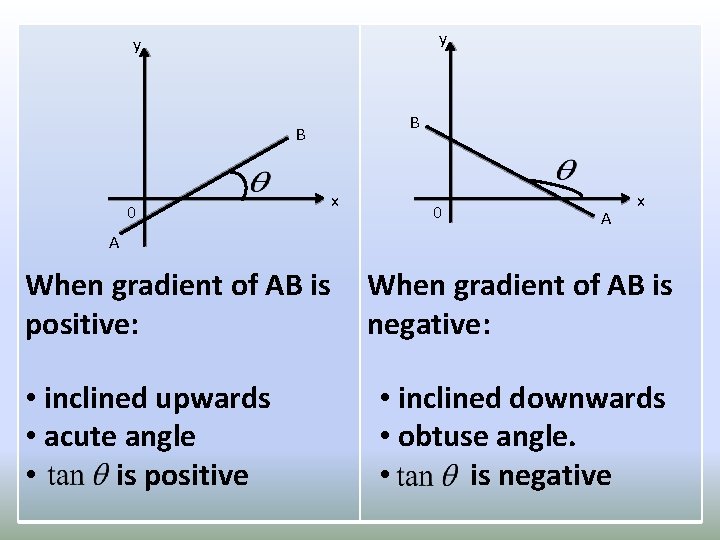
y y B B 0 x 0 A x A When gradient of AB is positive: • inclined upwards • acute angle • is positive When gradient of AB is negative: • inclined downwards • obtuse angle. • is negative
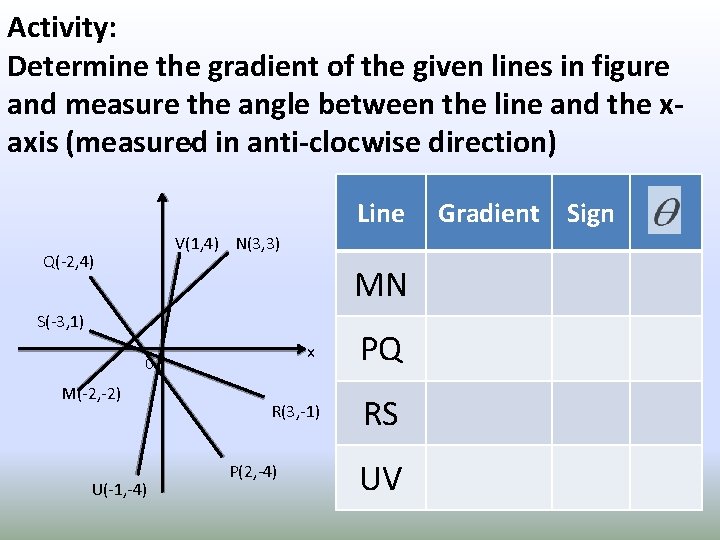
Activity: Determine the gradient of the given lines in figure and measure the angle between the line and the xy in anti-clocwise direction) axis (measured Line V(1, 4) N(3, 3) Q(-2, 4) MN S(-3, 1) x PQ R(3, -1) RS 0 M(-2, -2) U(-1, -4) P(2, -4) UV Gradient Sign

REMEMBER!!! The value of the gradient of a line: • Increases as the steepness increases • Is positive if it makes an acute angle • Is negative if it makes an obtuse angle
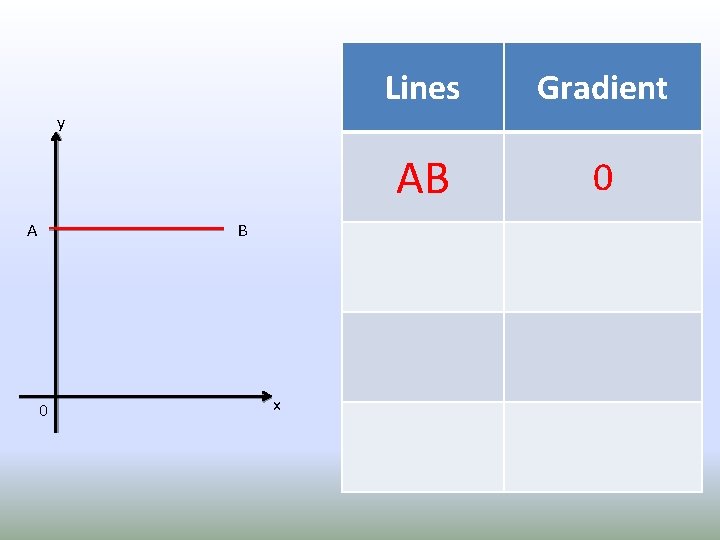
Lines Gradient AB 0 y A B 0 x
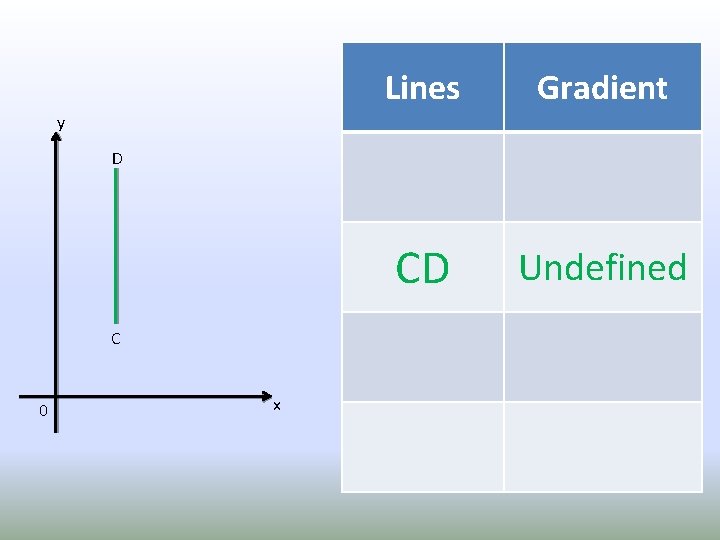
Lines Gradient CD Undefined y D C 0 x
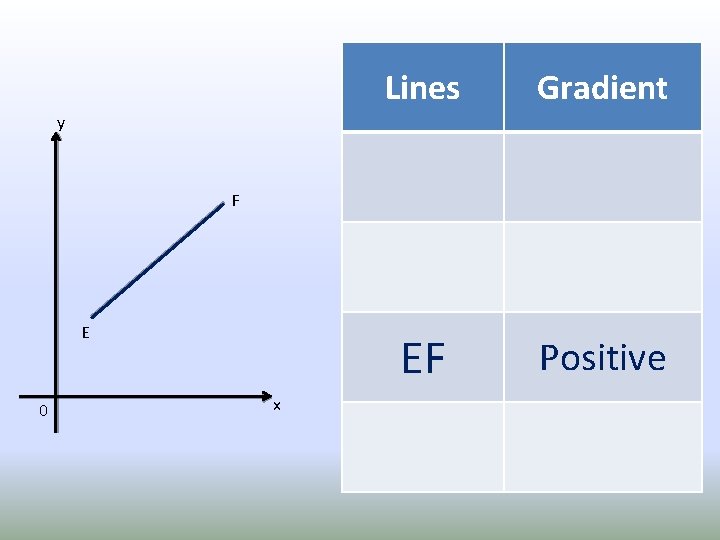
Lines Gradient EF Positive y F E 0 x
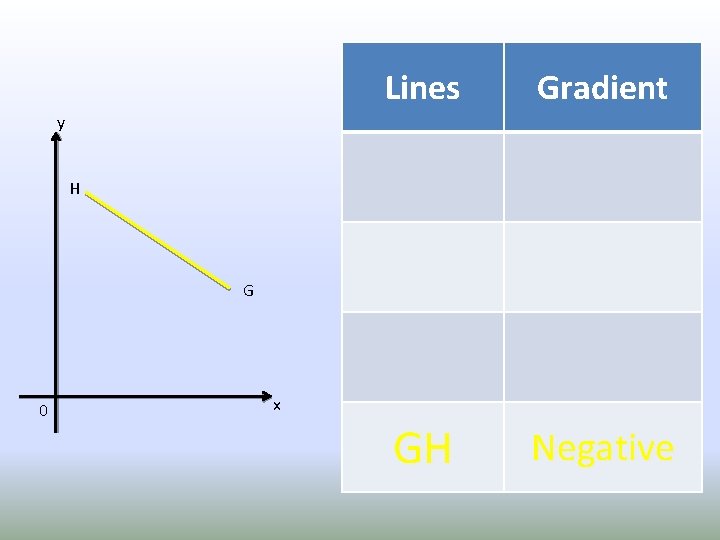
Lines Gradient GH Negative y H G 0 x
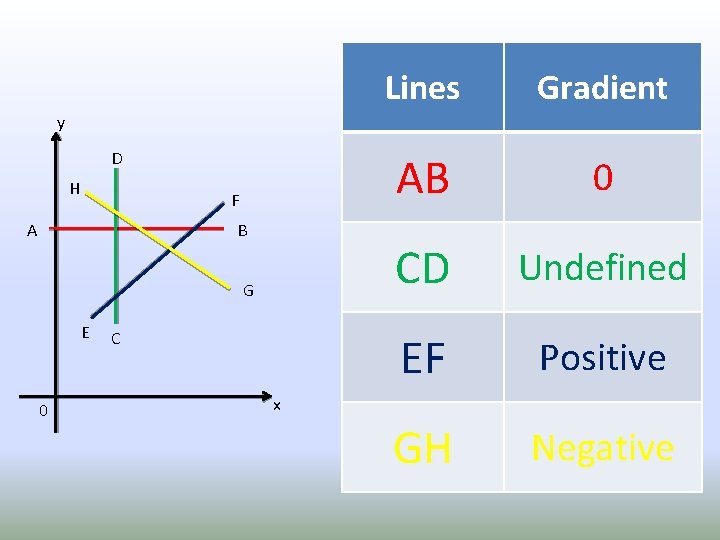
Lines Gradient AB 0 CD Undefined EF Positive GH Negative y D H F A B G E 0 C x
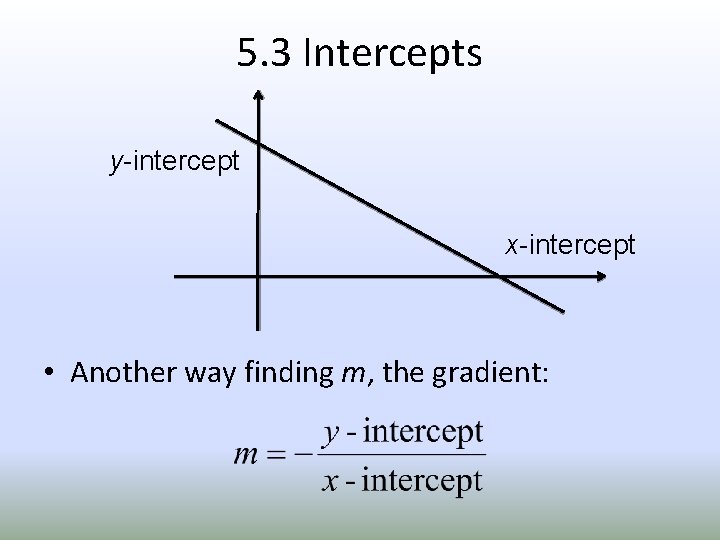
5. 3 Intercepts y-intercept x-intercept • Another way finding m, the gradient:

5. 4 Equation of a straight line • Slope intercept form y = mx + c • Point-slope form given 1 point and gradient: given 2 point:

5. 5 Parallel lines • When the gradient of two straight lines are equal, it can be concluded that the two straight lines are parallel. Example: Is the line 2 x-y=6 parallel to line 2 y=4 x+3? Solution: 2 x-y=6 y 2 y=4 x+3 y=2 x-6 gradient is 2. Since their gradient is same hence they are parallel.
- Slides: 23