Chapter 5 The Standard Deviation and the Normal

Chapter 5 The Standard Deviation and the Normal Model 1

68 -95 -99. 7 rule Mean and Standard Deviation (numerical) Histogram (graphical) 68 -95 -99. 7 rule 2

The 68 -95 -99. 7 rule; applies only to mound-shaped data 3

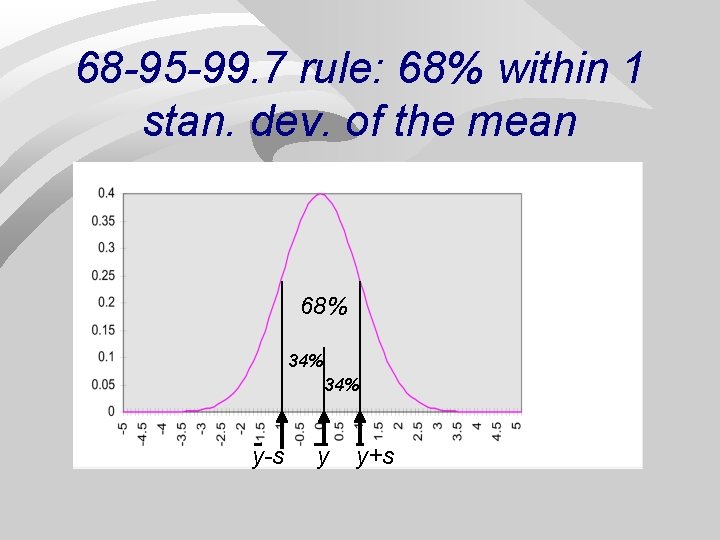
68 -95 -99. 7 rule: 68% within 1 stan. dev. of the mean 68% 34% y-s y y+s 4

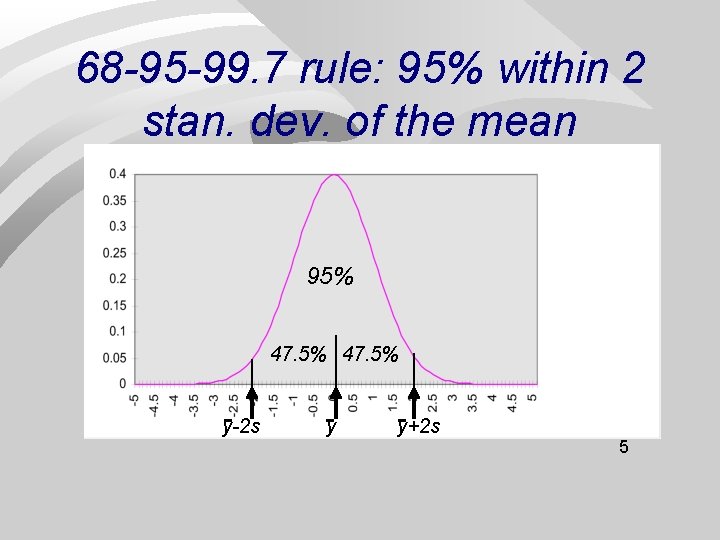
68 -95 -99. 7 rule: 95% within 2 stan. dev. of the mean 95% 47. 5% y-2 s y y+2 s 5

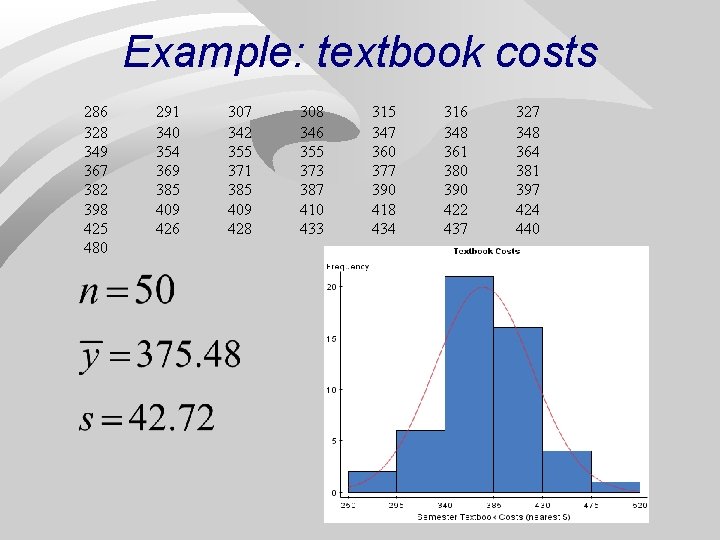
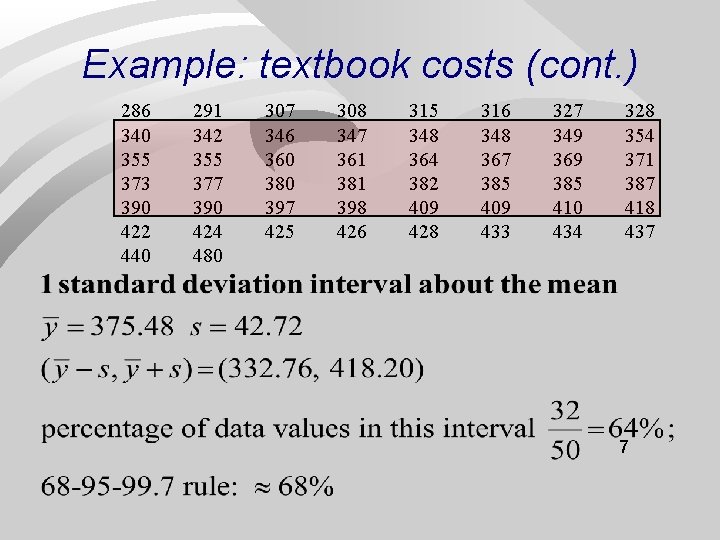
Example: textbook costs 286 328 349 367 382 398 425 480 291 340 354 369 385 409 426 307 342 355 371 385 409 428 308 346 355 373 387 410 433 315 347 360 377 390 418 434 316 348 361 380 390 422 437 327 348 364 381 397 424 440 6

Example: textbook costs (cont. ) 286 340 355 373 390 422 440 291 342 355 377 390 424 480 307 346 360 380 397 425 308 347 361 381 398 426 315 348 364 382 409 428 316 348 367 385 409 433 327 349 369 385 410 434 328 354 371 387 418 437 7

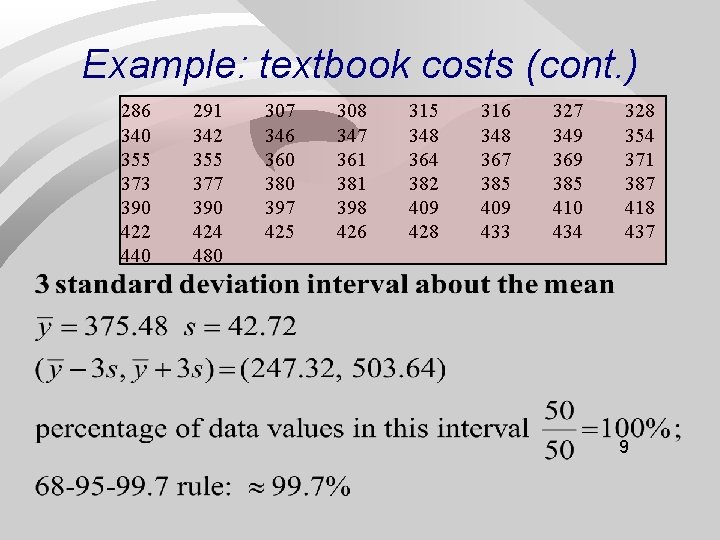
Example: textbook costs (cont. ) 286 340 355 373 390 422 440 291 342 355 377 390 424 480 307 346 360 380 397 425 308 347 361 381 398 426 315 348 364 382 409 428 316 348 367 385 409 433 327 349 369 385 410 434 328 354 371 387 418 437 8

Example: textbook costs (cont. ) 286 340 355 373 390 422 440 291 342 355 377 390 424 480 307 346 360 380 397 425 308 347 361 381 398 426 315 348 364 382 409 428 316 348 367 385 409 433 327 349 369 385 410 434 328 354 371 387 418 437 9

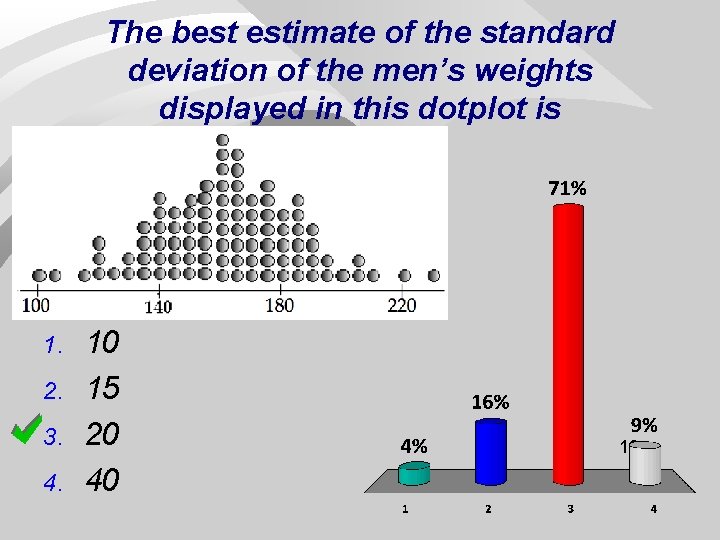
The best estimate of the standard deviation of the men’s weights displayed in this dotplot is 1. 2. 3. 4. 10 15 20 40 10

Changing Units of Measurement Shifting data and rescaling data, and how shifting and rescaling data affect graphical and numerical summaries of data.

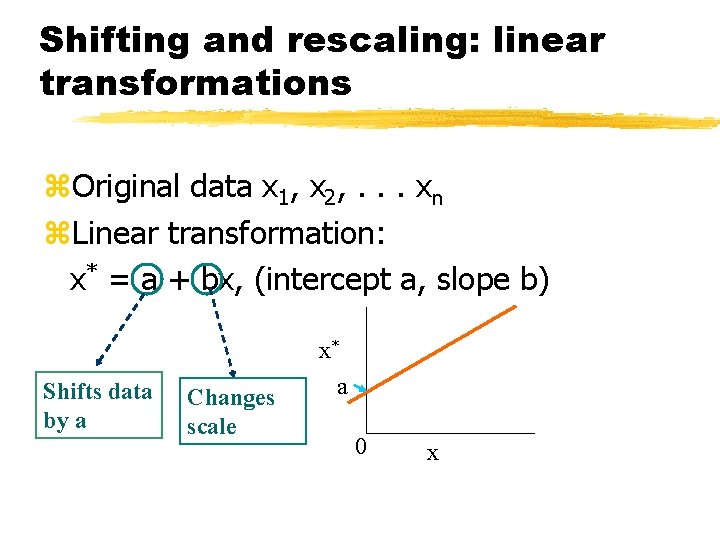
Shifting and rescaling: linear transformations z. Original data x 1, x 2, . . . xn z. Linear transformation: x* = a + bx, (intercept a, slope b) Shifts data by a Changes scale x* a 0 x

Linear Transformations 2. 54 32 12 40 100 00 0 a+ 9/5 x x* = 150 b Examples: Changing 1. from feet (x) to inches (x*): x*=12 x 2. from dollars (x) to cents (x*): x*=100 x 3. from degrees celsius (x) to degrees fahrenheit (x*): x* = 32 + (9/5)x 4. from ACT (x) to SAT (x*): x*=150+40 x 5. from inches (x) to centimeters (x*): x* = 2. 54 x

Shifting data only: b = 1 x* = a + x Adding the same value a to each value in the data set: changes the mean, median, Q 1 and Q 3 by a The standard deviation, IQR and variance are NOT CHANGED. y. Everything shifts together. y. Spread of the items does not change.

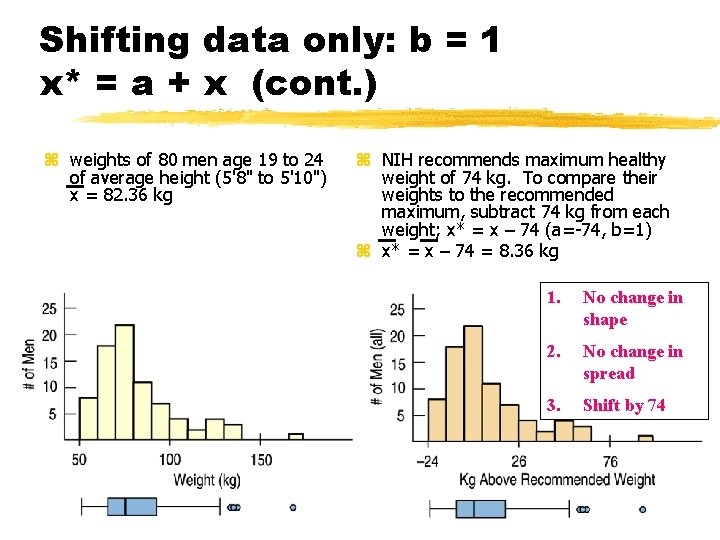
Shifting data only: b = 1 x* = a + x (cont. ) z weights of 80 men age 19 to 24 of average height (5'8" to 5'10") x = 82. 36 kg z NIH recommends maximum healthy weight of 74 kg. To compare their weights to the recommended maximum, subtract 74 kg from each weight; x* = x – 74 (a=-74, b=1) z x* = x – 74 = 8. 36 kg 1. No change in shape 2. No change in spread 3. Shift by 74

Shifting and Rescaling data: x* = a + bx, b > 0 Original x data: x 1, x 2, x 3, . . . , xn Summary statistics: mean x median m 1 st quartile Q 1 3 rd quartile Q 3 stand dev s variance s 2 IQR x* data: x* = a + bx x 1*, x 2*, x 3*, . . . , xn* Summary statistics: new mean x* = a + bx new median m* = a+bm new 1 st quart Q 1*= a+b. Q 1 new 3 rd quart Q 3* = a+b. Q 3 new stand dev s* = b s new variance s*2 = b 2 s 2 new IQR* = b IQR

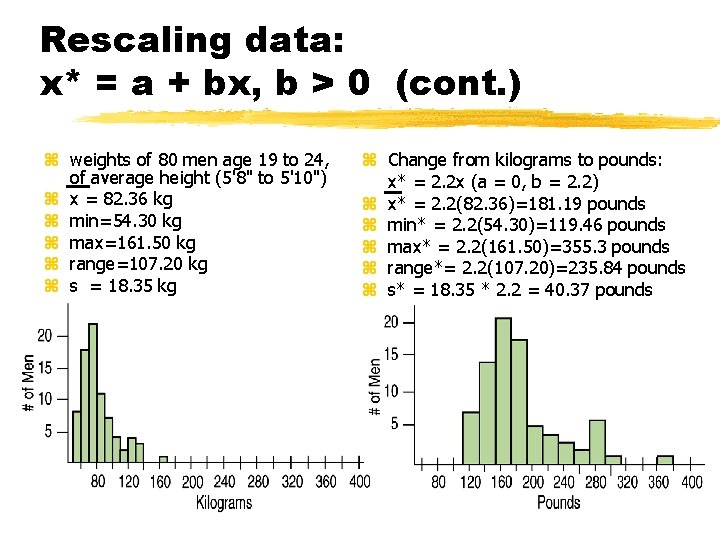
Rescaling data: x* = a + bx, b > 0 (cont. ) z weights of 80 men age 19 to 24, of average height (5'8" to 5'10") z x = 82. 36 kg z min=54. 30 kg z max=161. 50 kg z range=107. 20 kg z s = 18. 35 kg z Change from kilograms to pounds: x* = 2. 2 x (a = 0, b = 2. 2) z x* = 2. 2(82. 36)=181. 19 pounds z min* = 2. 2(54. 30)=119. 46 pounds z max* = 2. 2(161. 50)=355. 3 pounds z range*= 2. 2(107. 20)=235. 84 pounds z s* = 18. 35 * 2. 2 = 40. 37 pounds

Example of x* = a + bx 4 student heights in inches (x data) not 62, 64, 72 necessary! UNC x = 68 inches method s = 5. 89 inches Suppose we want centimeters instead: Go directly to x* = 2. 54 x this. NCSU (a = 0, b = 2. 54) method 4 student heights in centimeters: 157. 48 = 2. 54(62) 162. 56 = 2. 54(64) 187. 96 = 2. 54(74) 182. 88 = 2. 54(72) x* = 172. 72 centimeters s* = 14. 9606 centimeters Note that x* = 2. 54 x = 2. 54(68)=172. 2 s* = 2. 54 s = 2. 54(5. 89)=14. 9606

Example of x* = a + bx x data: Percent returns from 4 investments during 2003: 5%, 4%, 3%, 6% not x = 4. 5% necessary! s = 1. 29% Inflation during 2003: 2% x* data: Inflation-adjusted returns. Go directly to this x* = x – 2% (a=-2, b=1) x* data: 3% = 5% - 2% 2% = 4% - 2% 1% = 3% - 2% 4% = 6% - 2% x* = 10%/4 = 2. 5% s* = s = 1. 29% x* = x – 2% = 4. 5% – 2% s* = s = 1. 29% (note! that s* ≠ s – 2%) !!

Example z Original data x: Jim Bob’s jumbo watermelons from his garden have the following weights (lbs): 23, 34, 38, 44, 48, 55, 68, 72, 75 s = 17. 12; Q 1=37, Q 3 =69; IQR = 69 – 37 = 32 z Melons over 50 lbs are priced differently; the amount each melon is over (or under) 50 lbs is: z x* = x 50 (x* = a + bx, a=-50, b=1) -27, -16, -12, -6, -2, 5, 5, 18, 22, 25 s* = 17. 12; Q*1 = 37 - 50 =-13, Q*3 = 69 - 50 = 19 IQR* = 19 – (-13) = 32 NOTE: s* = s, IQR*= IQR

SUMMARY: Linear Transformations x* = a + bx z Linear transformations do not affect the shape of the distribution of the data -for example, if the original data is right-skewed, the transformed data is right-skewed

SUMMARY: Shifting and Rescaling data, x* = a + bx, b > 0

Z-scores: Standardized Data Values Measures the distance of a number from the mean in units of the standard deviation 24

z-score corresponding to y 25

n Exam 1: y 1 = 88, s 1 = 6; exam 1 score: 91 Exam 2: y 2 = 88, s 2 = 10; exam 2 score: 92 Which score is better? 26

Comparing SAT and ACT Scores SAT Math: Eleanor’s score 680 SAT mean =500 sd=100 n ACT Math: Gerald’s score 27 ACT mean=18 sd=6 n Eleanor’s z-score: z=(680 -500)/100=1. 8 n Gerald’s z-score: z=(27 -18)/6=1. 5 n Eleanor’s score is better. n 27

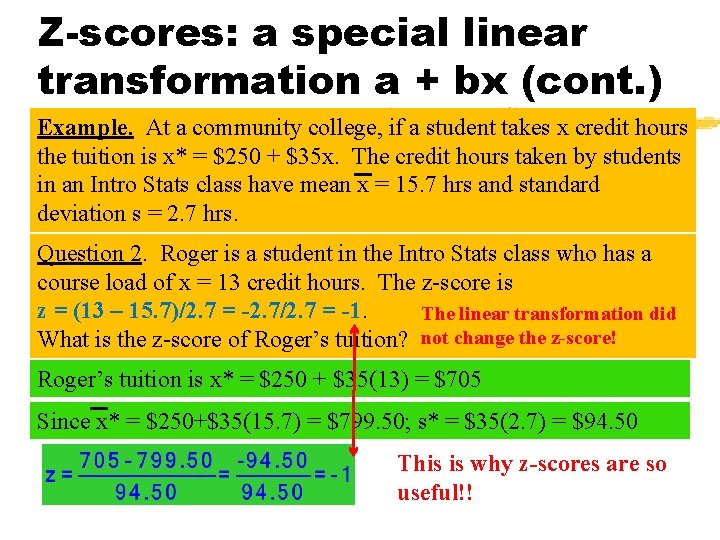
Z-scores: a special linear transformation a + bx Example. At a community college, if a student takes x credit hours the tuition is x* = $250 + $35 x. The credit hours taken by students in an Intro Stats class have mean x = 15. 7 hrs and standard deviation s = 2. 7 hrs. Question 1. A student’s tuition charge is $941. 25. What is the z-score of this tuition? x* = $250+$35(15. 7) = $799. 50; s* = $35(2. 7) = $94. 50

Z-scores: a special linear transformation a + bx (cont. ) Example. At a community college, if a student takes x credit hours the tuition is x* = $250 + $35 x. The credit hours taken by students in an Intro Stats class have mean x = 15. 7 hrs and standard deviation s = 2. 7 hrs. Question 2. Roger is a student in the Intro Stats class who has a course load of x = 13 credit hours. The z-score is z = (13 – 15. 7)/2. 7 = -2. 7/2. 7 = -1. The linear transformation did What is the z-score of Roger’s tuition? not change the z-score! Roger’s tuition is x* = $250 + $35(13) = $705 Since x* = $250+$35(15. 7) = $799. 50; s* = $35(2. 7) = $94. 50 This is why z-scores are so useful!!

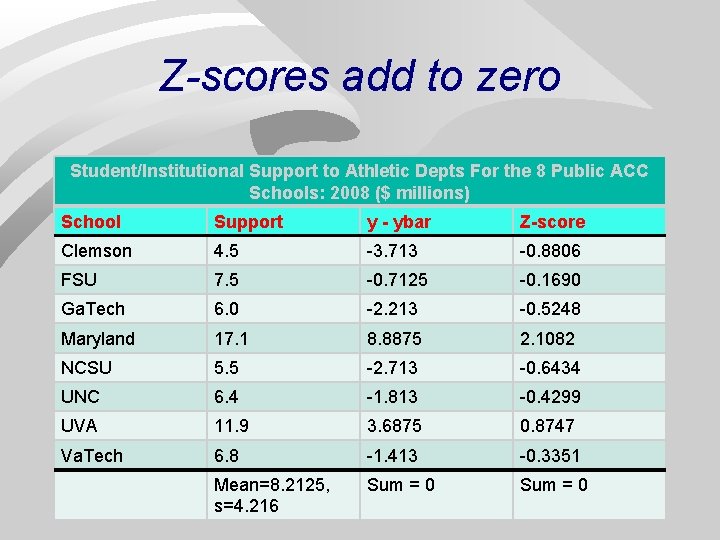
Z-scores add to zero Student/Institutional Support to Athletic Depts For the 8 Public ACC Schools: 2008 ($ millions) School Support y - ybar Z-score Clemson 4. 5 -3. 713 -0. 8806 FSU 7. 5 -0. 7125 -0. 1690 Ga. Tech 6. 0 -2. 213 -0. 5248 Maryland 17. 1 8. 8875 2. 1082 NCSU 5. 5 -2. 713 -0. 6434 UNC 6. 4 -1. 813 -0. 4299 UVA 11. 9 3. 6875 0. 8747 Va. Tech 6. 8 -1. 413 -0. 3351 Mean=8. 2125, s=4. 216 Sum = 0 30

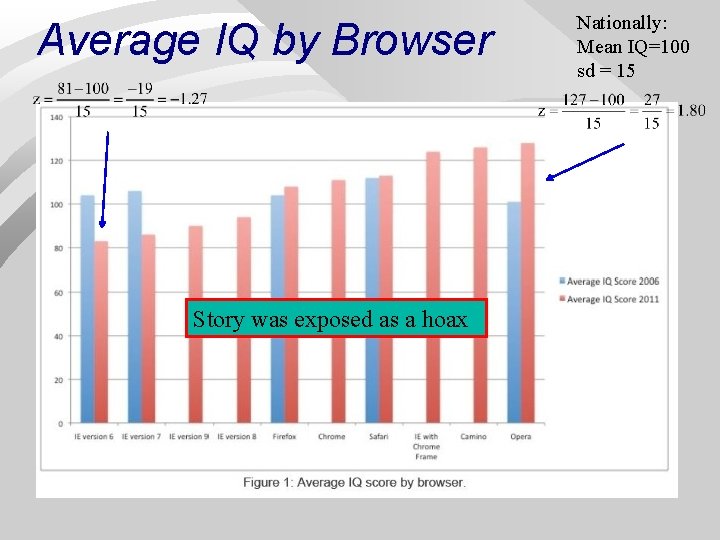
Average IQ by Browser Nationally: Mean IQ=100 sd = 15 Story was exposed as a hoax 31

NORMAL PROBABILITY MODELS The Most Important Model for Data in Statistics 32

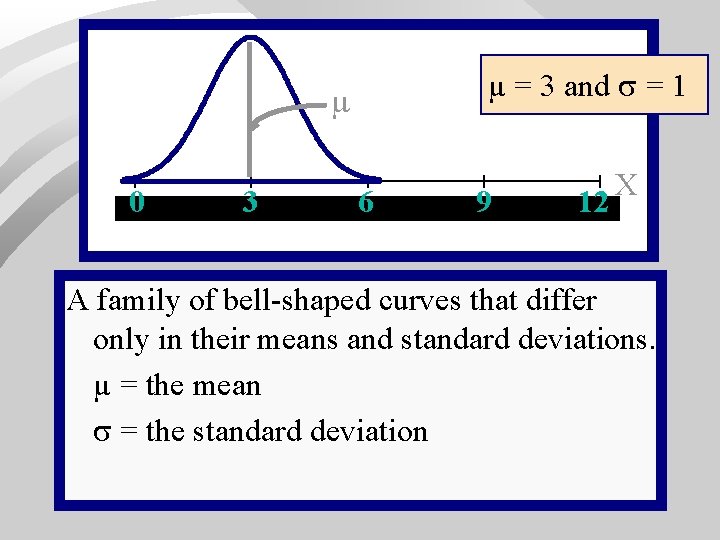
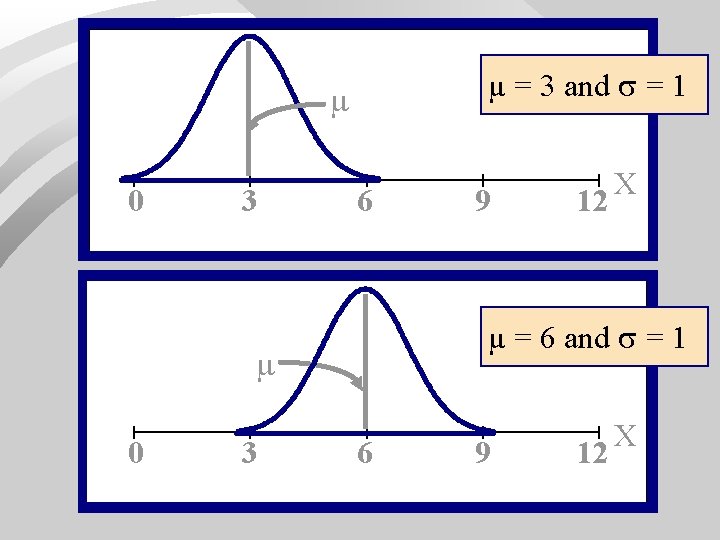
µ = 3 and = 1 0 3 6 8 9 12 X A family of bell-shaped curves that differ only in their means and standard deviations. µ = the mean = the standard deviation 33

Normal Probability Models The mean, denoted , can be any number n The standard deviation can be any nonnegative number n The total area under every normal model curve is 1 n There are infinitely many normal distributions n 34

Total area =1; symmetric around µ 35

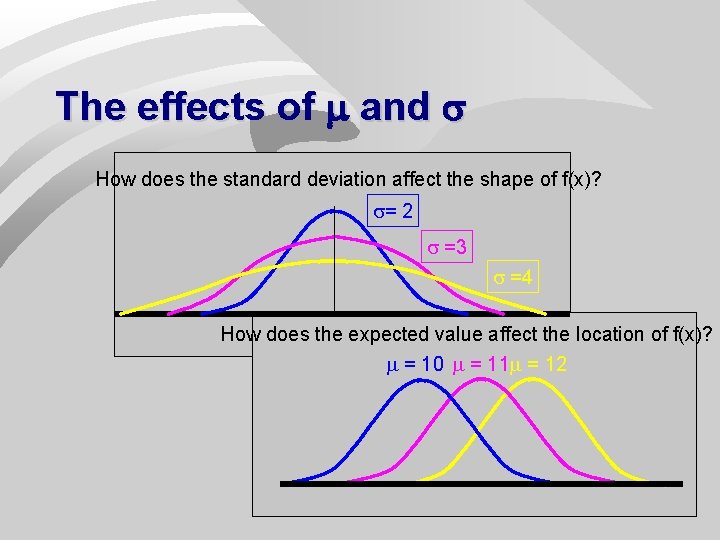
The effects of m and How does the standard deviation affect the shape of f(x)? = 2 =3 =4 How does the expected value affect the location of f(x)? = 10 = 11 = 12 36

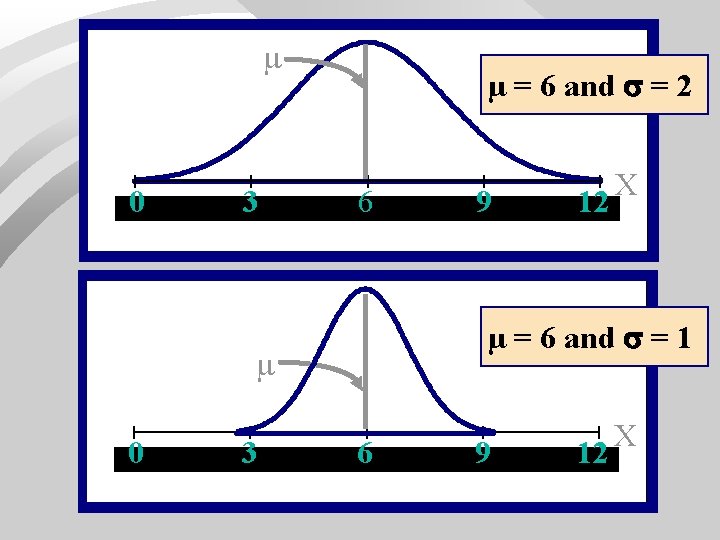
µ = 3 and = 1 0 3 6 3 12 µ = 6 and = 1 0 9 X 6 9 12 X 37

0 3 µ = 6 and = 2 6 8 3 12 µ = 6 and = 1 0 9 X 6 8 9 12 X 38

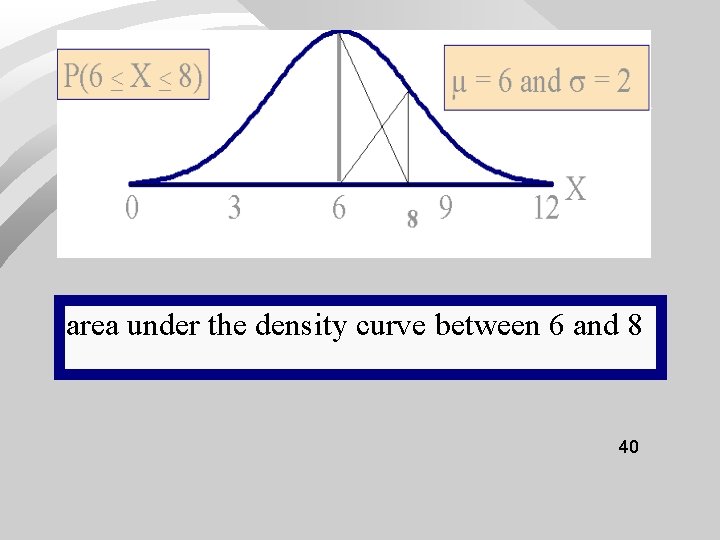
µ = 6 and = 2 0 3 6 9 12 X area under the density curve between 6 and 8. 39

area under the density curve between 6 and 8 40

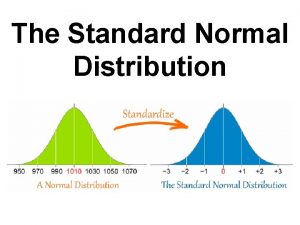
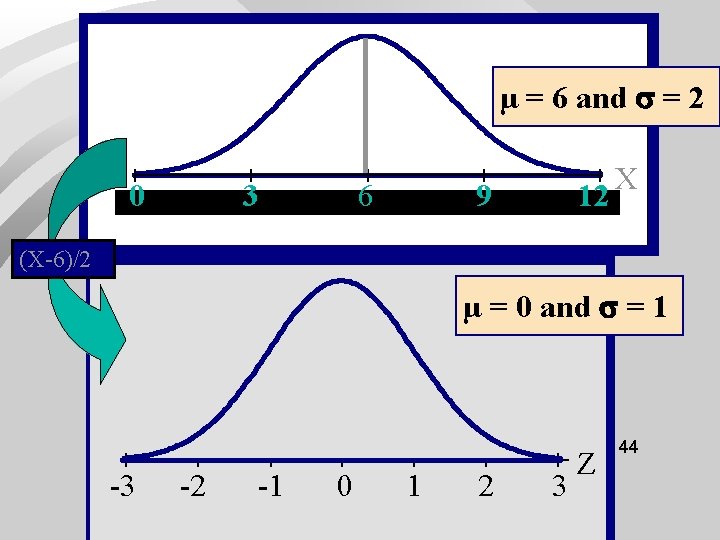
Standardizing Suppose X~N( n Form a new random variable by subtracting the mean from X and dividing by the standard deviation : (X n This process is called standardizing the random variable X. 41 n

Standardizing (cont. ) (X is also a normal random variable; we will denote it by Z: Z = (X n has mean 0 and standard deviation 1: E(Z) = = 0; SD(Z) = = . n The probability distribution of Z is called 42 the standard normal distribution. n

Standardizing (cont. ) If X has mean and stand. dev. , standardizing a particular value of x tells how many standard deviations x is above or below the mean . n Exam 1: =80, =10; exam 1 score: 92 Exam 2: =80, =8; exam 2 score: 90 Which score is better? n 43

µ = 6 and = 2 0 3 6 8 9 12 X (X-6)/2 µ = 0 and = 1. 5 -3 -2 -1 . 5 0 1 2 3 Z 44

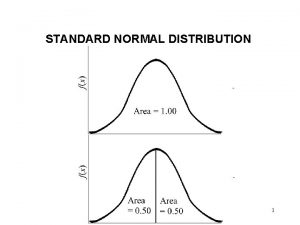
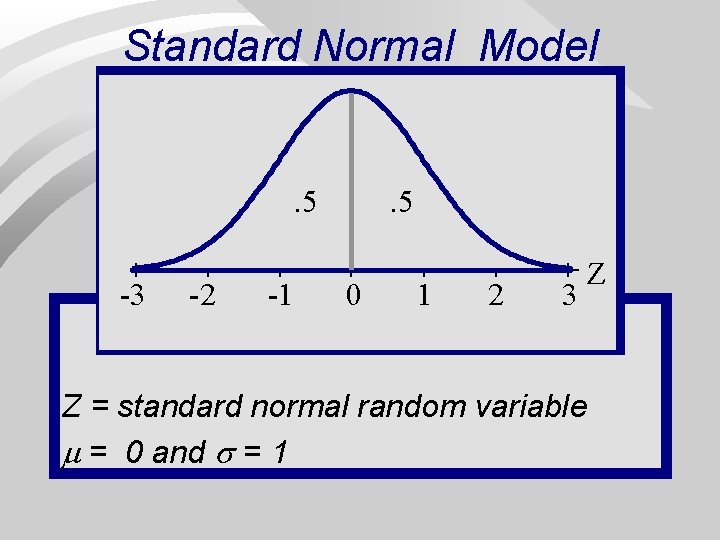
Standard Normal Model . 5 -3 -2 -1 . 5 0 1 2 3 Z = standard normal random variable = 0 and = 1 Z 45

Important Properties of Z #1. The standard normal curve is symmetric around the mean 0 #2. The total area under the curve is 1; so (from #1) the area to the left of 0 is 1/2, and the area to the right of 0 is 1/2 46

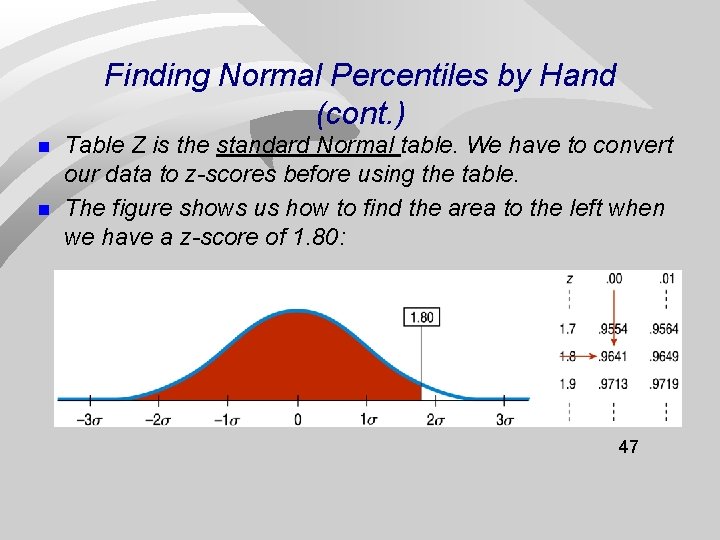
Finding Normal Percentiles by Hand (cont. ) n n Table Z is the standard Normal table. We have to convert our data to z-scores before using the table. The figure shows us how to find the area to the left when we have a z-score of 1. 80: 47

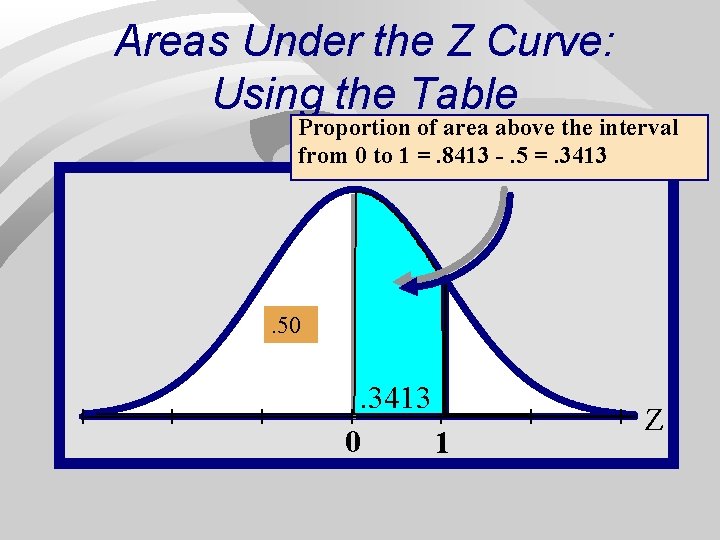
Areas Under the Z Curve: Using the Table Proportion of area above the interval from 0 to 1 =. 8413 -. 5 =. 3413 . 50 . 3413. 1587 0 1 Z 48

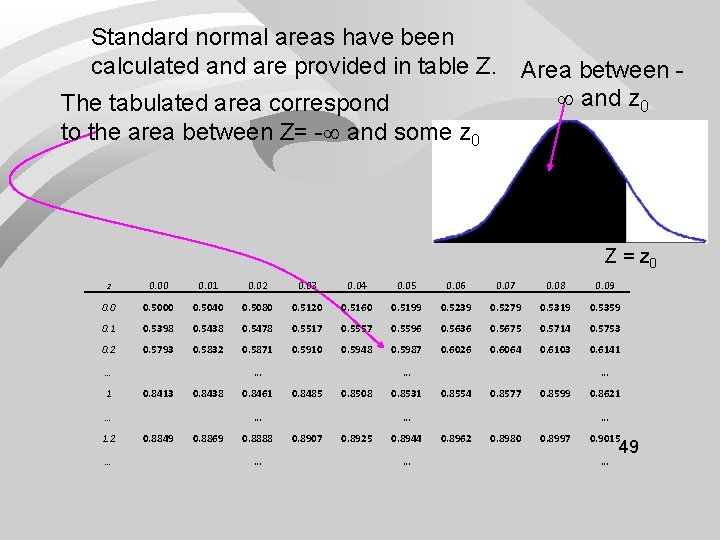
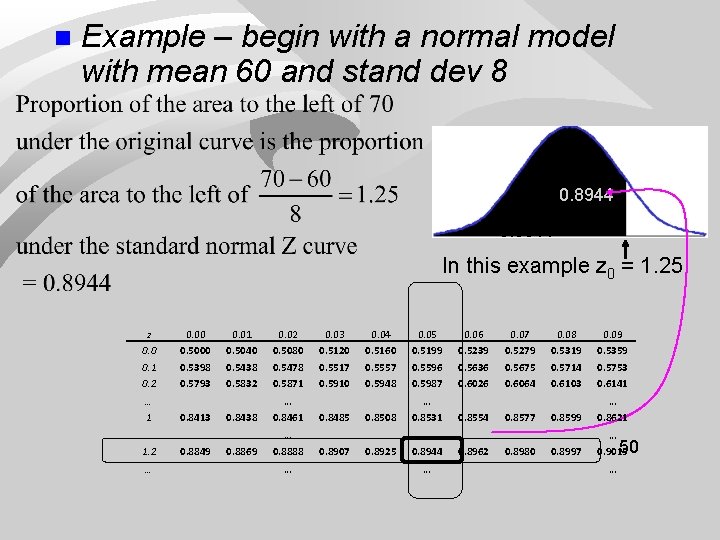
Standard normal areas have been calculated and are provided in table Z. Area between and z 0 The tabulated area correspond to the area between Z= - and some z 0 Z = z 0. 00 0. 01 0. 02 0. 03 0. 04 0. 05 0. 06 0. 07 0. 08 0. 09 0. 0 0. 5000 0. 5040 0. 5080 0. 5120 0. 5160 0. 5199 0. 5239 0. 5279 0. 5319 0. 5359 0. 1 0. 5398 0. 5438 0. 5478 0. 5517 0. 5557 0. 5596 0. 5636 0. 5675 0. 5714 0. 5753 0. 2 0. 5793 0. 5832 0. 5871 0. 5910 0. 5948 0. 5987 0. 6026 0. 6064 0. 6103 0. 6141 … 0. 8413 0. 8438 … 1. 2 … 0. 8461 … 0. 8485 0. 8508 … 0. 8849 0. 8869 0. 8888 … 0. 8531 … 0. 8554 0. 8577 0. 8599 … 0. 8907 0. 8925 0. 8944 … 0. 8621 … 0. 8962 0. 8980 0. 8997 0. 9015 … 49

n Example – begin with a normal model with mean 60 and stand dev 8 0. 8944 In this example z 0 = 1. 25 z 0. 0 0. 1 0. 2 … 1. 2 … 0. 00 0. 5000 0. 5398 0. 5793 0. 8413 0. 8849 0. 01 0. 5040 0. 5438 0. 5832 0. 02 0. 5080 0. 5478 0. 5871 0. 8438 … 0. 8461 0. 8869 … 0. 8888 … 0. 03 0. 5120 0. 5517 0. 5910 0. 8485 0. 8907 0. 04 0. 5160 0. 5557 0. 5948 0. 05 0. 5199 0. 5596 0. 5987 0. 8508 … 0. 8531 0. 8925 … 0. 8944 … 0. 06 0. 5239 0. 5636 0. 6026 0. 8554 0. 8962 0. 07 0. 5279 0. 5675 0. 6064 0. 8577 0. 8980 0. 08 0. 5319 0. 5714 0. 6103 0. 09 0. 5359 0. 5753 0. 6141 0. 8599 … 0. 8621 0. 8997 … 0. 9015 50 …

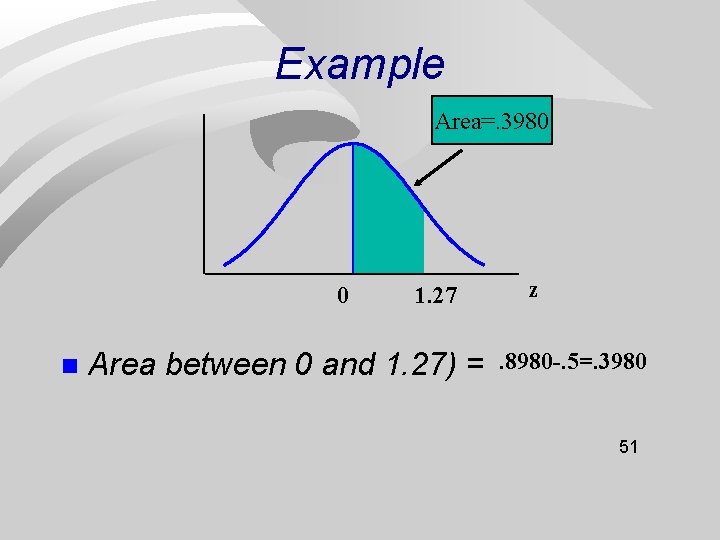
Example Area=. 3980 0 n 1. 27 Area between 0 and 1. 27) = z. 8980 -. 5=. 3980 51

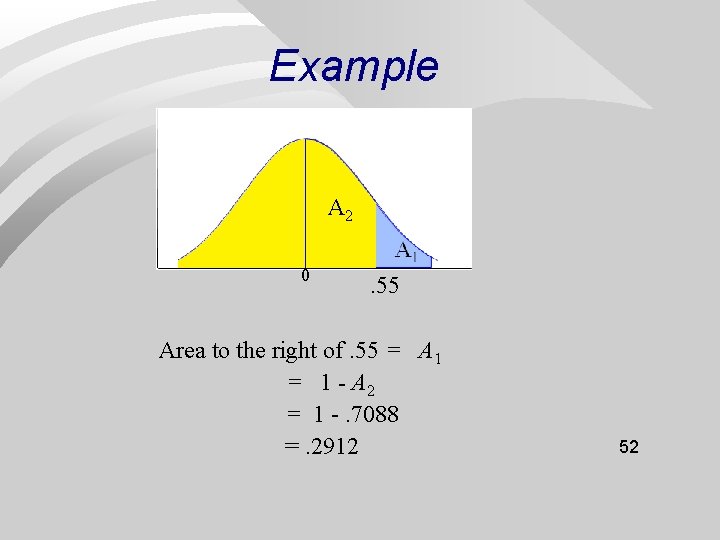
Example A 2 0 . 55 Area to the right of. 55 = A 1 = 1 - A 2 = 1 -. 7088 =. 2912 52

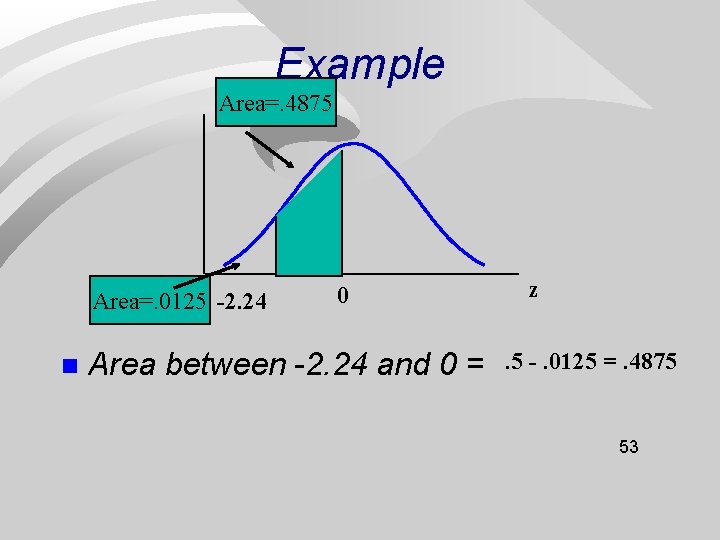
Example Area=. 4875 Area=. 0125 -2. 24 n 0 Area between -2. 24 and 0 = z. 5 -. 0125 =. 4875 53

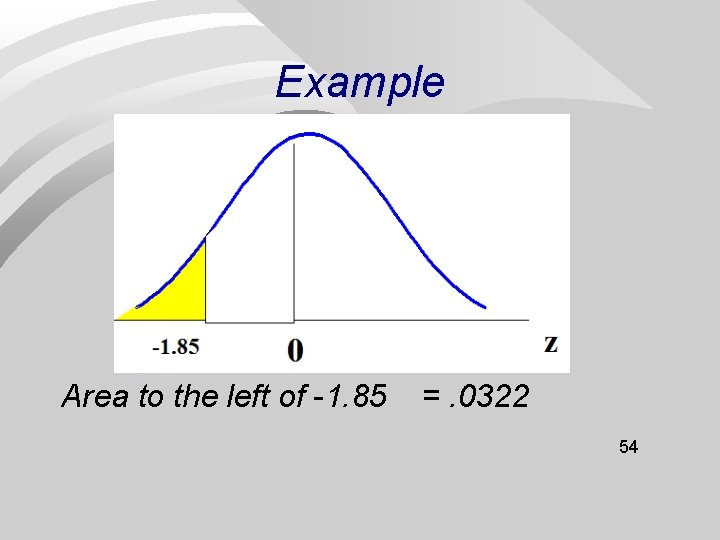
Example Area to the left of -1. 85 =. 0322 54

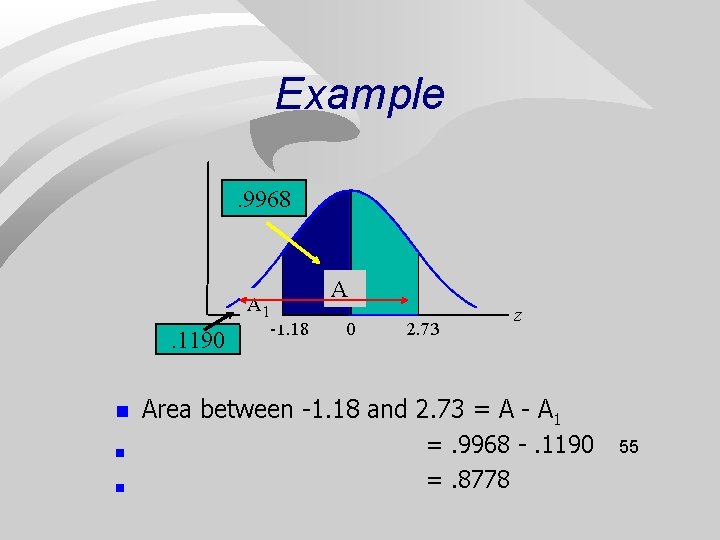
Example. 9968 A 1 . 1190 n n n -1. 18 A 0 A 2 2. 73 z Area between -1. 18 and 2. 73 = A - A 1 =. 9968 -. 1190 =. 8778 55

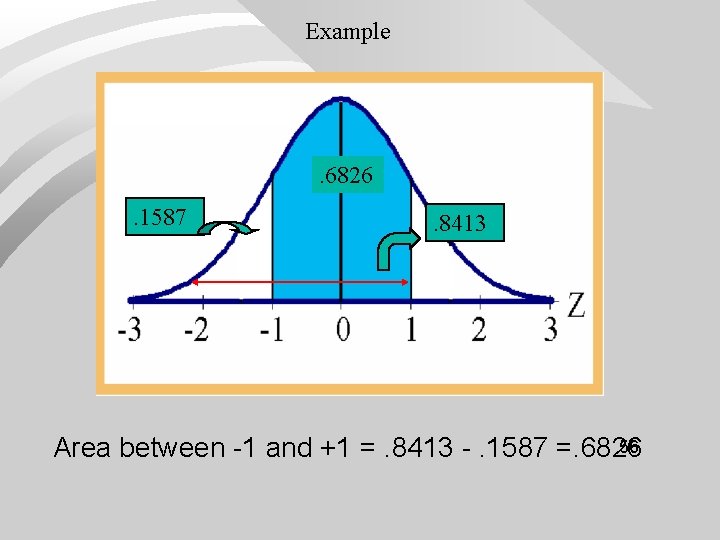
Example . 6826. 1587 . 8413 56 Area between -1 and +1 =. 8413 -. 1587 =. 6826

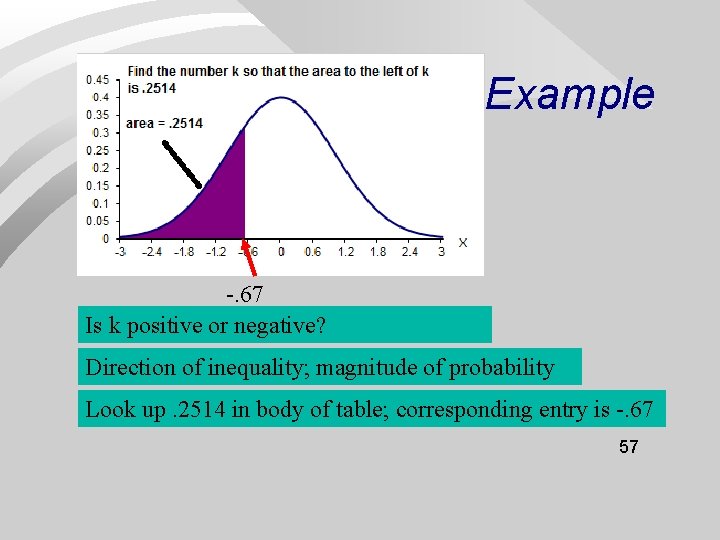
Example -. 67 Is k positive or negative? Direction of inequality; magnitude of probability Look up. 2514 in body of table; corresponding entry is -. 67 57

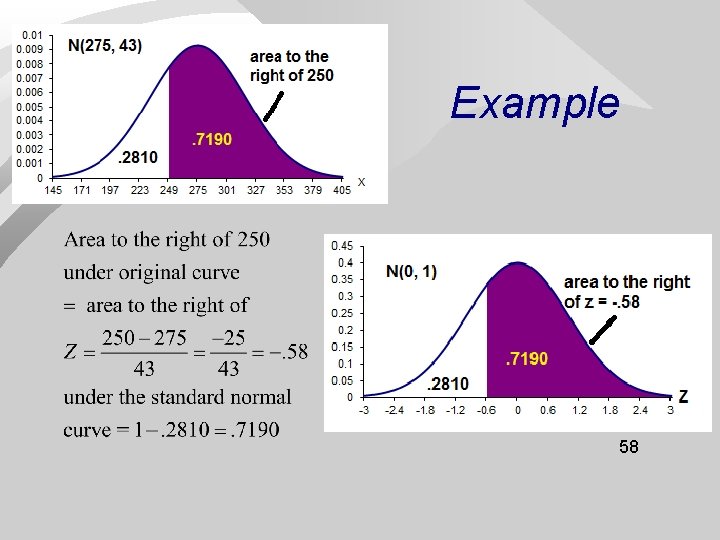
Example 58

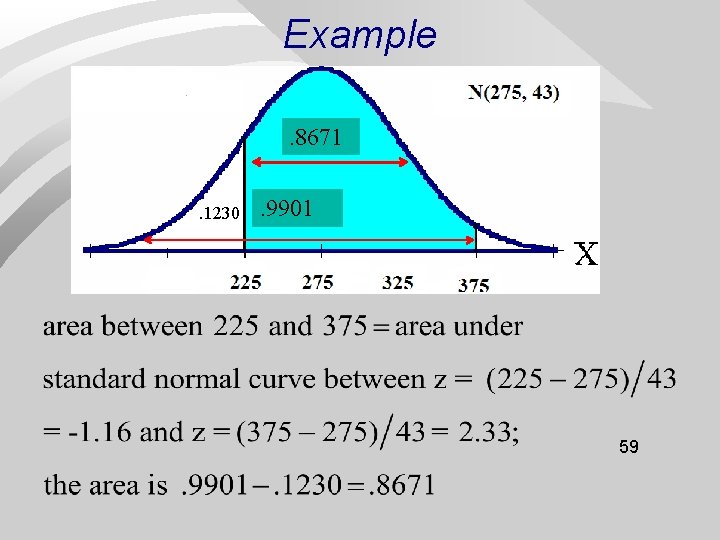
Example. 8671. 1230 . 9901 59

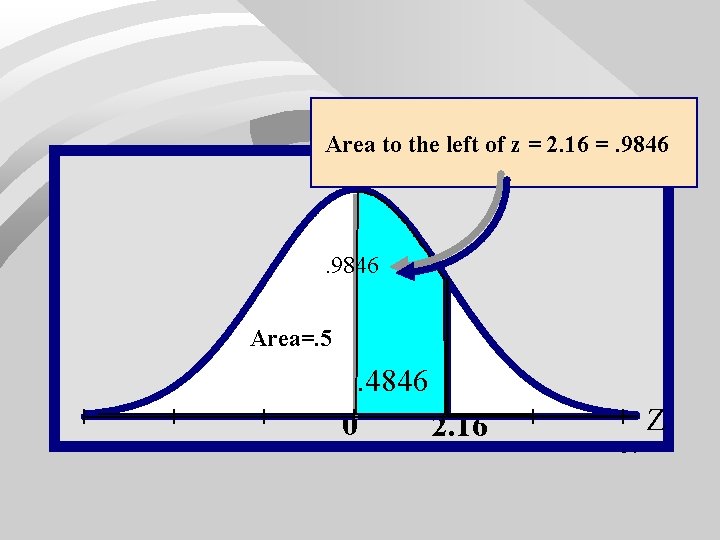
N(275, 43); find k so that area to the left is. 9846 60

Area to the left of z = 2. 16 =. 9846 Area=. 5 . 4846. 1587 0 2. 16 Z 61

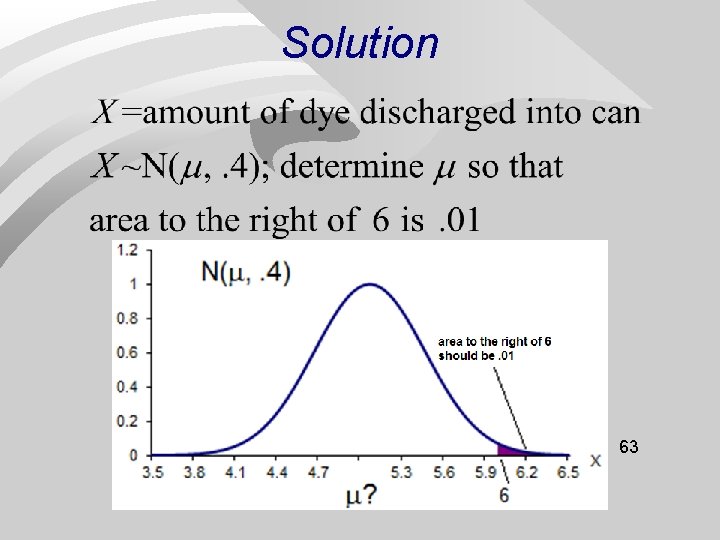
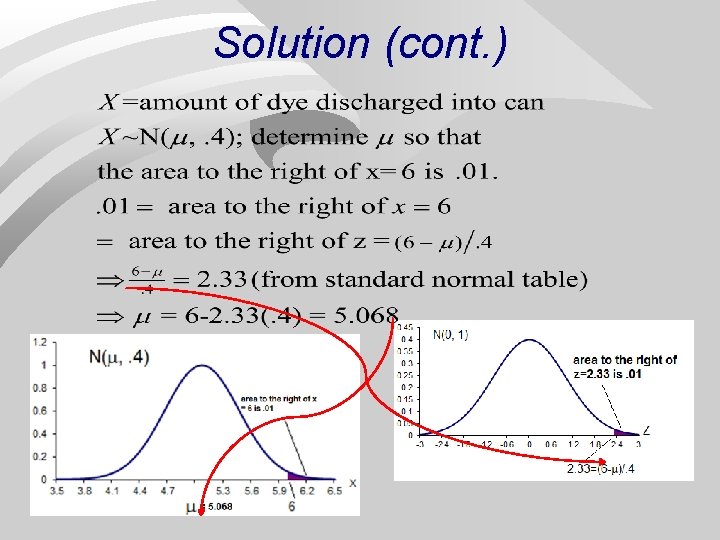
Example Regulate blue dye for mixing paint; machine can be set to discharge an average of ml. /can of paint. n Amount discharged: N( , . 4 ml). If more than 6 ml. discharged into paint can, shade of blue is unacceptable. n Determine the setting so that only 1% of 62 the cans of paint will be unacceptable n

Solution 63

Solution (cont. ) 64

Normal Distributions n A random variable X with mean and standard deviation is normally distributed if its probability density function is given by 65

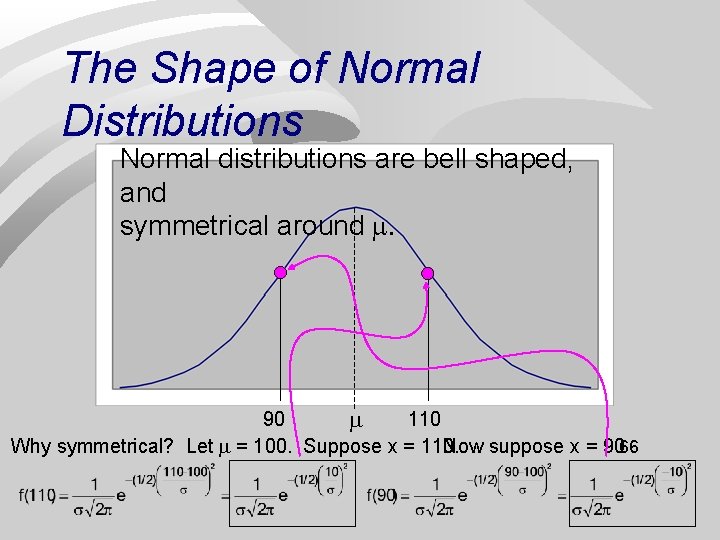
The Shape of Normal Distributions Normal distributions are bell shaped, and symmetrical around . 90 110 Why symmetrical? Let = 100. Suppose x = 110. Now suppose x = 9066

Are You Normal? Normal Probability Plots Checking your data to determine if a normal model is appropriate 67

Are You Normal? Normal Probability Plots When you actually have your own data, you must check to see whether a Normal model is reasonable. n Looking at a histogram of the data is a good way to check that the underlying distribution is roughly unimodal and symmetric. n 68

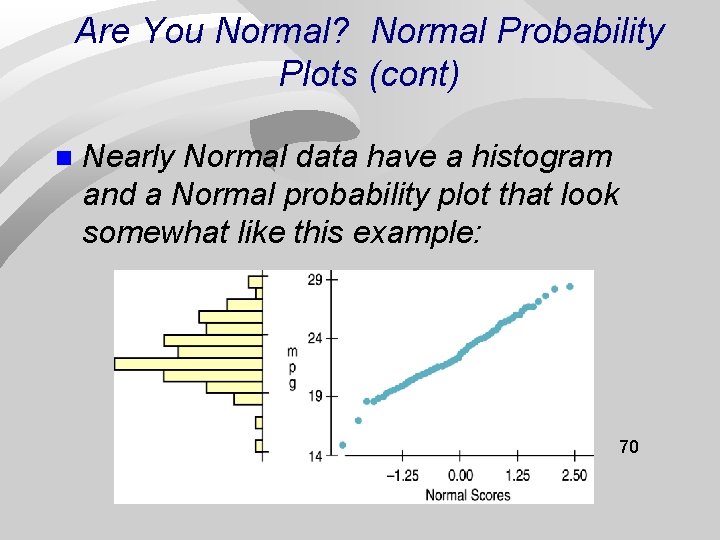
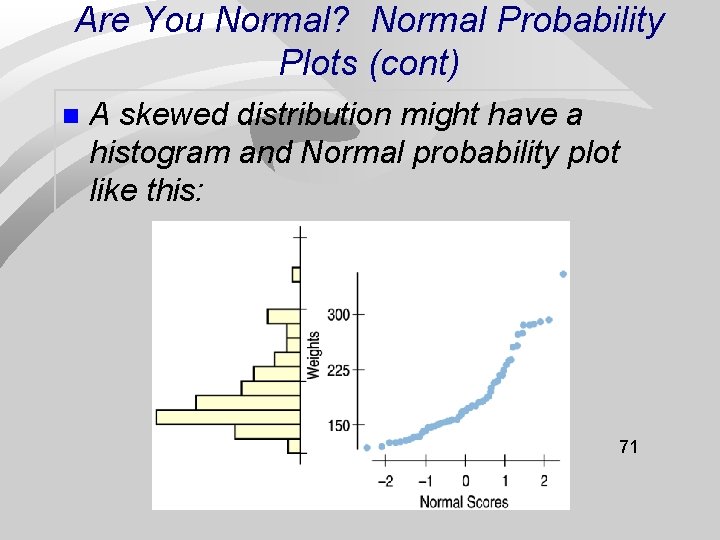
Are You Normal? Normal Probability Plots (cont) A more specialized graphical display that can help you decide whether a Normal model is appropriate is the Normal probability plot. n If the distribution of the data is roughly Normal, the Normal probability plot approximates a diagonal straight line. Deviations from a straight line indicate 69 that the distribution is not Normal. n

Are You Normal? Normal Probability Plots (cont) n Nearly Normal data have a histogram and a Normal probability plot that look somewhat like this example: 70

Are You Normal? Normal Probability Plots (cont) n A skewed distribution might have a histogram and Normal probability plot like this: 71